增强S形波纹管内压稳定性分析方法

2022-08-12霍世慧许红卫朱卫平

火箭推进 2022年4期

霍世慧，许红卫，朱卫平，袁喆

(1.液体火箭发动机技术重点实验室，陕西西安 710100；2.上海大学上海市应用数学和力学研究所，上海 200072；3.西安航空学院，陕西西安 710077)

0 引言

波纹管作为一种补偿性能良好、使用维护简单的补偿器，在石油、化工、电力、城建和航空航天等领域得到了广泛的应用。根据实际工作环境的不同，波纹管结构多种多样，增强S形波纹管是在传统U形波纹管的基础上将波峰与波谷间的直线段改为斜线设计而成，并通过增强环的引入使得结构承载能力明显提升，广泛应用于航天和核工业等极端高压工作环境。然而，增强S形波纹管的设计分析相对复杂，理论公式需要经过反复试验修正，得到的近似公式精度也相对较低，目前仍未形成规律性的成熟经验。

波纹管在内压过大的情况下会丧失稳定性，使结构疲劳寿命和位移补偿能力大大降低，最常见的失稳模式是柱失稳和平面失稳。柱失稳是指波纹管中心线或轴线整体侧向偏移，这是长细比较大的波纹管的常见失稳现象，类似于压杆的屈曲，其临界载荷分为弹性和非弹性两个区域，即表示一系列具有相同直径、厚度和波形的波纹管发生柱屈曲的临界压力值，随着波纹管长度的增加，曲线从非弹性向弹性过渡。当波数较少或长细比较小时，则易出现一个或多个波纹横截面发生移动或偏移的现象，即平面失稳，造成这种屈曲的主要原因在于子午向弯曲应力过大，在波峰顶和谷底形成塑性铰。

圆柱壳在内压作用下柱失稳的临界压力与承受轴向作用均布压力时相同，这一现象最早由Haringx通过实验发现，文献[4-7]等在对C形、Ω形、U形等波纹管整体刚度问题深入理论研究基础上，对这一现象进行了理论解析证明，为波纹管临界失稳压力的计算提供了理论依据。陈晔发现波纹管在内压和轴向位移的联合作用下，波谷将首先进入塑性状态，提出将环板中出现塑性区作为平面失稳的判据。钟玉平等通过试验研究证明膨胀节制造商协会标准(EJMA)中的平面失稳极限设计压力计算方法同样适用于外压作用工况，并指出内压和外压作用下平面失稳的机理是一致的，同时压缩位移降低了外压平面失稳的临界压力。文献[12-13]开展了拉伸及外压载荷作用下金属波纹管稳定性的试验研究和有限元分析，给出了拉伸和外压载荷下金属波纹管的临界载荷。张玉田分别开展了外压、拉伸及其综合载荷作用下薄壁波纹管周向稳定性研究。谈卓君等开展了多层U形波纹管轴向刚度及临界载荷的有限元分析，分析中同时考虑波纹管层间接触条件及波峰到波谷壁厚的变化，并通过与试验结果的对比，验证了分析的合理性。文献[16-17]研究了金属波纹管的刚度及其流固耦合特性，给出了金属波纹管流固耦合分析方法。徐学军等针对增强S形波纹管建立了一种结构耐压强度分析方法。国内外的研究主要集中在U形金属波纹管结构的内、外压和轴向拉伸作用结构极限承载能力的分析和试验方面，涉及耐高压增强S形波纹管的研究相对较少，未能形成有效的分析方法总结。

本文将针对增强S形波纹管，结合有限元分析和EJMA相关规范，给出该类型波纹管柱失稳临界内压的解析分析方法，为增强S形波纹管的结构设计分析提供依据。

1 增强S形波纹管结构说明

图1所示为增强S形波纹管，主要包括S形波纹管、增强环和直边段增强环，增强环直接提高了结构整体的耐压能力，直边段增强环位于结构的上下两端，用于与外部结构的连接。

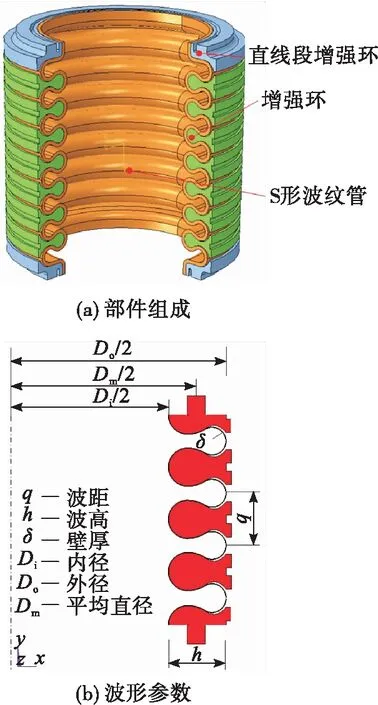
图1 增强S形波纹管

增强S形波纹管总长127.5 mm，最小通径80 mm；波纹管波距为14.7 mm，波高为17.4 mm，共含8层薄壁结构，总厚度为2.4 mm。S形波纹管材料为0Cr18Ni10Ti，增强环与直线段增强环材料为S—06钢，两种材料力学性能参数如表1所示。

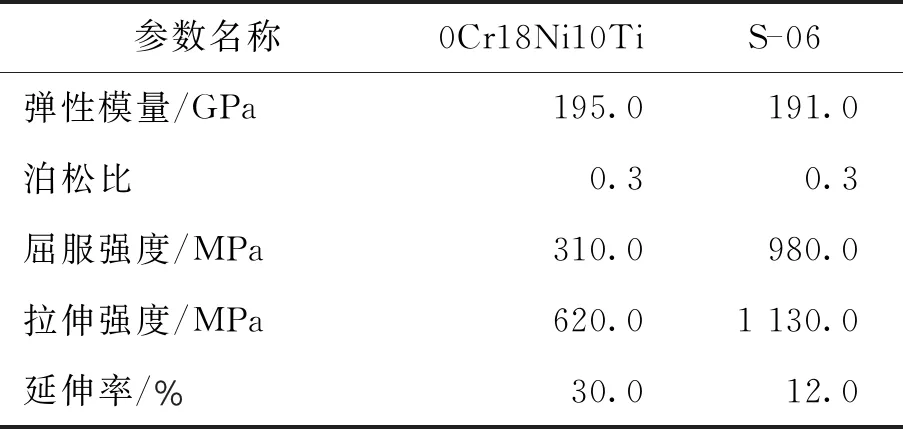
表1 增强S形波纹管材料参数

2 增强S形波纹管稳定性分析方法

波纹管的失稳主要包括平面失稳和柱失稳两种表现形式。平面失稳是由于应力过大，导致结构在波谷和波峰位置形成了“塑性铰”，直接影响波纹管的疲劳寿命，但针对增强S形波纹管，增强环对波纹管起到直接保护作用，不可能发生平面失稳现象，因此下面的分析将重点关注增强S形波纹管的柱失稳情况。

柱失稳是指波纹管轴线变弯，中间波纹有较大的横向偏移，波距发生明显变化的现象。柱失稳分析主要采用如式(1)所示的Euler公式。

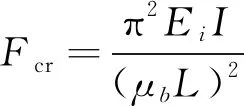
(1)

式中：为波纹管弯曲刚度；为长度折算系数，主要与波纹管端面支撑相关，参考EJMA标准，针对“法兰等连接件刚度远大于波纹管管口的刚度”按固支约束条件处理，取=05，并对“带初始转角和横向位移的刚性连接端”或“可转动和移动的刚性连接端”，引入边界影响系数=()，其中为连接端最大转角，单位为rad；为波纹管长度。

设定增强S形波纹管由个波距为的波纹管构成，波纹管平均直径为，由此可得增强S形波纹管柱失稳的临界内压，具体表达如式(2)所示，下面将分别给出增强S形波纹管弯曲刚度和边界影响系数的确定方式。

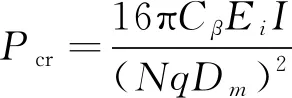
(2)

2.1 波纹管弯曲刚度的确定

波纹管弯曲变形过程中，结构一侧处于压缩变形状态，对应的另一侧处于拉伸变形状态，弯曲刚度的理论解析主要通过轴向拉、压刚度的等效换算获得。图2所示为增强S形波纹管弯曲变形示意，将波纹管等效为长度、平均直径、壁厚的薄壁圆筒，设圆筒转角和弯矩的增量分别记为Δ和Δ，轴向位移增量记为Δ=,+1-,(=1,2,…)，由此可得

图2 增强S形波纹管弯曲变形

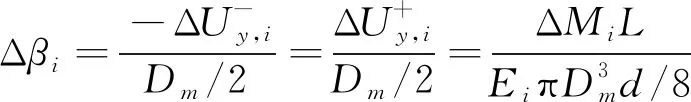
(3)

(4)

等效薄壁圆筒弯曲刚度主要通过轴向拉、压刚度换算得到，其压缩位移增量和载荷可表示为式(5)和式(6)。

(5)

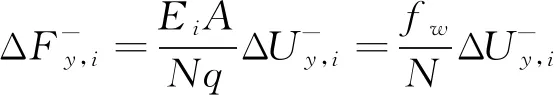
(6)

拉伸位移增量和载荷可表示为式(7)和式(8)。

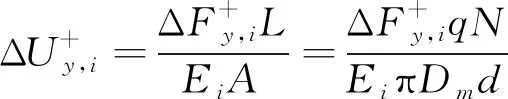
(7)

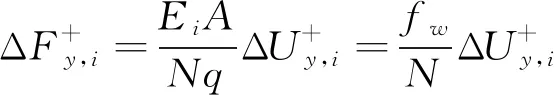
(8)

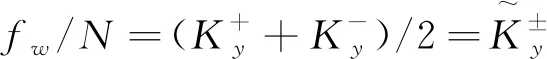
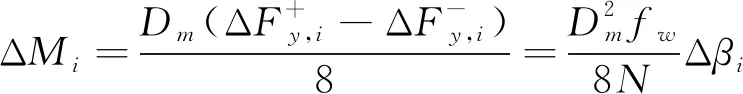
(9)

由式(4)和式(9)可以获得波纹管整体弯曲刚度表达式如式(10)所示，其中波纹管单波轴向刚度由有限元数值仿真分析结果获得，至此式(2)中增强S形波纹管柱失稳的临界内压可表达为式(11)。

(10)

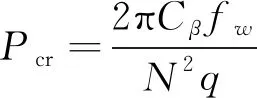
(11)

2.2 波纹管边界影响系数

内压作用下薄壁圆柱壳轴线稳定控制方程如式(12)所示。

(12)

式中()为轴线挠曲函数，其通解为

()=cos+sin++

(13)

根据式(14)所示转角方程和式(15)边界条件，可以解得相关系数如式(16)所示。

′()=-sin+cos+

(14)

(0)=，′(0)=，()=0，′()=0

(15)

(16)

将式(16)代入式(13)，得到内压作用下薄壁圆柱壳挠曲度的解。圆柱壳失稳的条件是挠度趋向无穷大，即要求式(16)中至少有一项趋向无穷大，由此可以解得最小临界压力如式(17)所示。

(17)

以上求解过程表明，只要是两端固支边界条件，按标准的特征值问题求解失稳临界压力，所得结果与连接端是否转动和移动无关。但根据经验和试验测试结果分析，EJMA标准认为波纹管承压后当其波距超过承压前的1.15倍时，屈曲就已经发生，即实际临界载荷小于式(17)结果，其减小量就需要通过修正系数来控制。

圆柱壳结构转动示意如图3所示，圆柱壳下端面由点转动至点，圆柱壳转角为，轴向位移量为。

图3 圆柱壳结构转动示意

在小位移条件下(=)，机构运动引起的端面转动与移动的关系如式(18)所示，中点挠度可表示为式(19)。

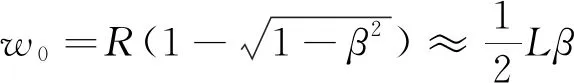
(18)

(19)

依据EJMA标准，将波距增加1.15倍(相当于挠曲线转角增加1.15倍)作为失稳的起点，由此可得中点挠度增量与圆柱壳长度的关系如式(20)所示。

Δ=0125Δ=(2)

(20)

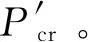
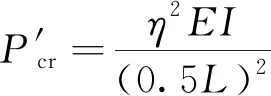
(21)

将式(21)与式(17)相比得

(22)

于是便得到波纹管边界影响系数的修正值，如式(23)所示。

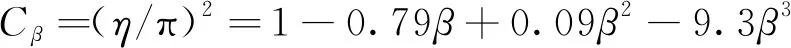
(23)

3 算例

针对图1给出的增强S形波纹管开展结构柱失稳最小临界压力分析，波纹管工作压力为35 MPa，摇摆角度为10°，由式(23)确定波纹管边界影响系数为0.814 2。基于有限元软件ABAQUS开展增强S形波纹管刚度特性分析，根据波纹管自身结构特点和载荷的对称性，建立如图4所示二维轴对称模型，波纹管材料采用双线性随动强化本构关系，模型上端施加轴向约束，下端施加轴向拉伸或压缩位移载荷，波纹管层间及其与增强环之间均定义为“面-面”接触关系，摩擦系数选取为0.12。通过施加一定的轴向位移，求出由此产生的轴向约束反力，从而获得增强S形波纹管结构轴向伸缩力学特性。

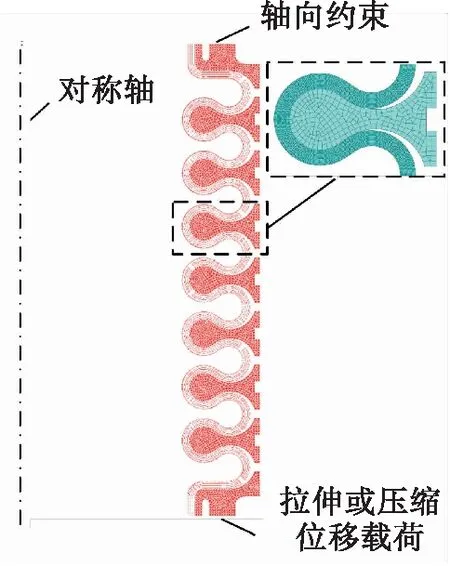
图4 有限元模型及其边界条件

增强S形波纹管轴向拉压曲线如图5所示，轴向拉伸载荷作用下，增强S形波纹管表现出非线性状态，初始阶段波纹管轴向约束力与拉伸位移的线性度较好，波纹管表现出“高刚度”状态；随着拉伸载荷的增大，波纹管局部进入屈服，呈现出软化的现象，表现出“低刚度”状态。轴向压缩载荷作用下，增强S形波纹管的非线性特征更加显著，表现出强非线性状态。与轴向拉伸曲线相同，波纹管在进入塑性屈服前，轴向约束力与压缩位移线性度较好，波纹管表现出“高刚度”状态，而在进入塑性屈服以后，波纹管呈现出软化现象，刚度发生下降。但经历一段“低刚度”状态后，当波纹管波峰与增强环外侧圆弧端面完全贴合时，波纹管达到一种如图6所示的新的稳定状态，从而使得压缩刚度陡增。

图5 增强S形波纹管轴向拉压曲线

图6 波纹管轴向压缩局部贴合状态

拉伸与压缩载荷作用下，增强S形波纹管均呈现出非线性特征，在柱失稳临界压力的分析中，整体结构弯曲刚度由拉压刚度的最小值确定。结合有限元分析结果，确定增强S形波纹管单波轴向刚度为12 152 N/mm，代入式(2)获得摇摆角为10°工况增强S形波纹管柱失稳临界压力为70 MPa，安全系数为2.0。波纹管轴向刚度分析中综合考虑了材料弹塑性、边界非线性、内压、大位移和拉压不对称等因素的影响，并在临界载荷分析中引入边界影响系数，临界压力分析方法较为完整地考虑了结构的各种影响因素，因此采用本文提出方法开展增强S形波纹管结构稳定性分析时，柱失稳安全系数不必取得很大。