对数线性插值土工颗粒分析方法

沈捍明

(中铁十二局集团第七工程有限公司 湖南长沙 410004)

1 前言

土工试验评定级配特性时，需要知道质量百分比P小于某一特定值m的特征粒径d(P＜m)来计算曲率系数、不均匀系数等参数。但是在试验过程中，筛网孔径固定且不连续，不可能直接测定d(P＜m)。工程中一般采用间接测定di(P＜mi)及di＋1(P＜mi＋1)，其中di和di＋1分别对应标准筛径，并合理选择mi及mi＋1，使m∈(mi，mi＋1)，将m线性内插入[(mi，di(P＜mi)]与[mi＋1，di＋1(P＜mi＋1)]点间，从而求得d(P＜m)。该方法是基于m与d(P＜m)的线性坐标系，但筛径尺寸从102mm变化至10－3mm，数量级跨度较大，在此坐标系下，相邻已知坐标点间距分布极不均匀，数据呈现非线性关系。工程中的筛分曲线展绘已考虑该问题，并采用了半对数坐标来显著体现曲线变化趋势，因此在特征粒径推定时若仍采用线性插值，其估计值将产生较大偏差[1－3]。

2 插值原理

如图1所示，设数据x经过对数运算后，位于对数坐标轴lgx上。A、B、C三点为实际测得的三个数据点，其坐标分别为(lgxA，yA)、(lgxB，yB)、(lgxC，yC)。在该坐标系下连接A、C点，过B点做水平线，与直线AC交于点B′，则B′点为y＝yB对应的对数线性内插点。根据线性内插关系:

图1 对数坐标线性插值示意

式(2)即为按对数坐标线性插值的计算公式，按指数规律变化，其与式(1)的线性内插方法不同。在已知A(xA，yA)、C(xC，yC)及B点纵坐标yC后，即可通过该式推算B点横坐标xB′。

3 偏差分析

3.1 “跳点法”计算插值偏差

采用插值方式对数据进行预测需给定对其偏差测定的方法，以评估插值精度，这是目前大多数数据插值处理所缺失的。土工筛分试验中，单次试验测定数据较少，考虑采用原始数据构造“跳点法”校核插值精度:如图2所示，设A、B、C、D为实测数据点，首先假设B点未知，AC点采用式(2)插值推算出B′点，再比对B与B′点位偏差值ΔB；假设C点未知，采用式(2)推算出C′点，比对C与C′点位偏差ΔC。依此类推，直至遍历所有点位。该方法可以校核除首末点外的所有点位偏差[4－6]。

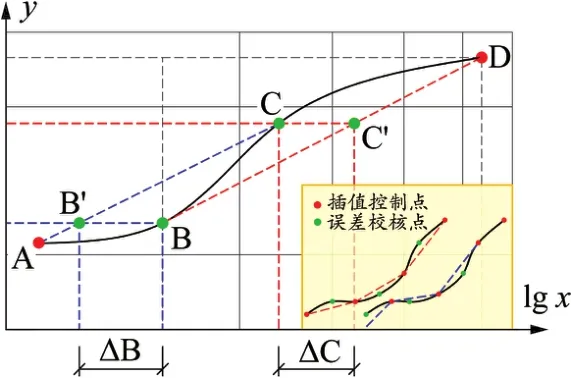
图2 跳点校核示意

3.2 偏差分析参数选定

由前述可知，采用“跳点法”，可先按式(3)逐个计算各点位的相对偏差δ。

在插值精度理想的情况下，δ应趋于0。样本整体的平均相对偏差越小，样本标准差σ越小，其表征插值方法对于源数据的适应性越好，性能越稳定。和σ分别按式(4)、式(5)计算。

由于标准筛径从150 mm变化至0.007 5 mm，数据变化跨度较大，虽相对偏差δ为无量纲量，考虑插值精度有限，可能存在相对偏差尺度变动较大情况，故还需采用式(6)计算变异系数辅以评估。

3.3 均值接近零时的变异系数优化

基于此，在当趋于0时，在保证式(6)中cv单调性不变的前提下，降缓其值增长速率，则考虑对其取对数处理。鉴于最小筛径为10－4数量级，最大筛径为102数量级，故对数底数采用104变换后cv在10－1至100数量级间浮动，较易辨别其变化特征，则定义:

3.4 偏差系数

由前述可知，评估插值方法的偏差时，、σ、cv均越小越好。但由式(7)计算变异系数时，可能出现负数，单纯取三者代数和可能存在正负抵消的情况。借鉴样本标准差定义方法，此处定义偏差系数Ψ有:

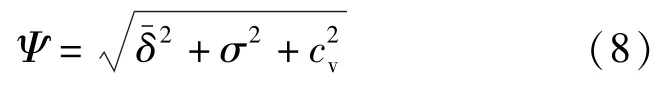
其中，、σ、cv分别由式(4)、式(5)、式(7)求得。在实际工程中，对于同一数据点，利用“跳点法”，分别采用线性插值和对数线性插值计算样本的偏差系数，取偏差系数较小的插值方法确定的插值参数作为估计值。

4 应用实例

4.1 数据偏差分析

以大张高铁改DIK184＋000～改DIK187＋150段路基填料的44组土工筛分试验数据作为样本，以实测的小于 40、20、10、5、2、1、0.5、0.25、0.75 mm粒径质量百分比作为真值，分别采用线性插值法和对数线性插值法反算相应粒径，并与真值粒径进行对比，计算过程和比对结果分别见表1～表4[7]。

表1 线性插值计算

表2 对数线性插值计算

表3 各粒组线性插值数据偏差分析

续表3

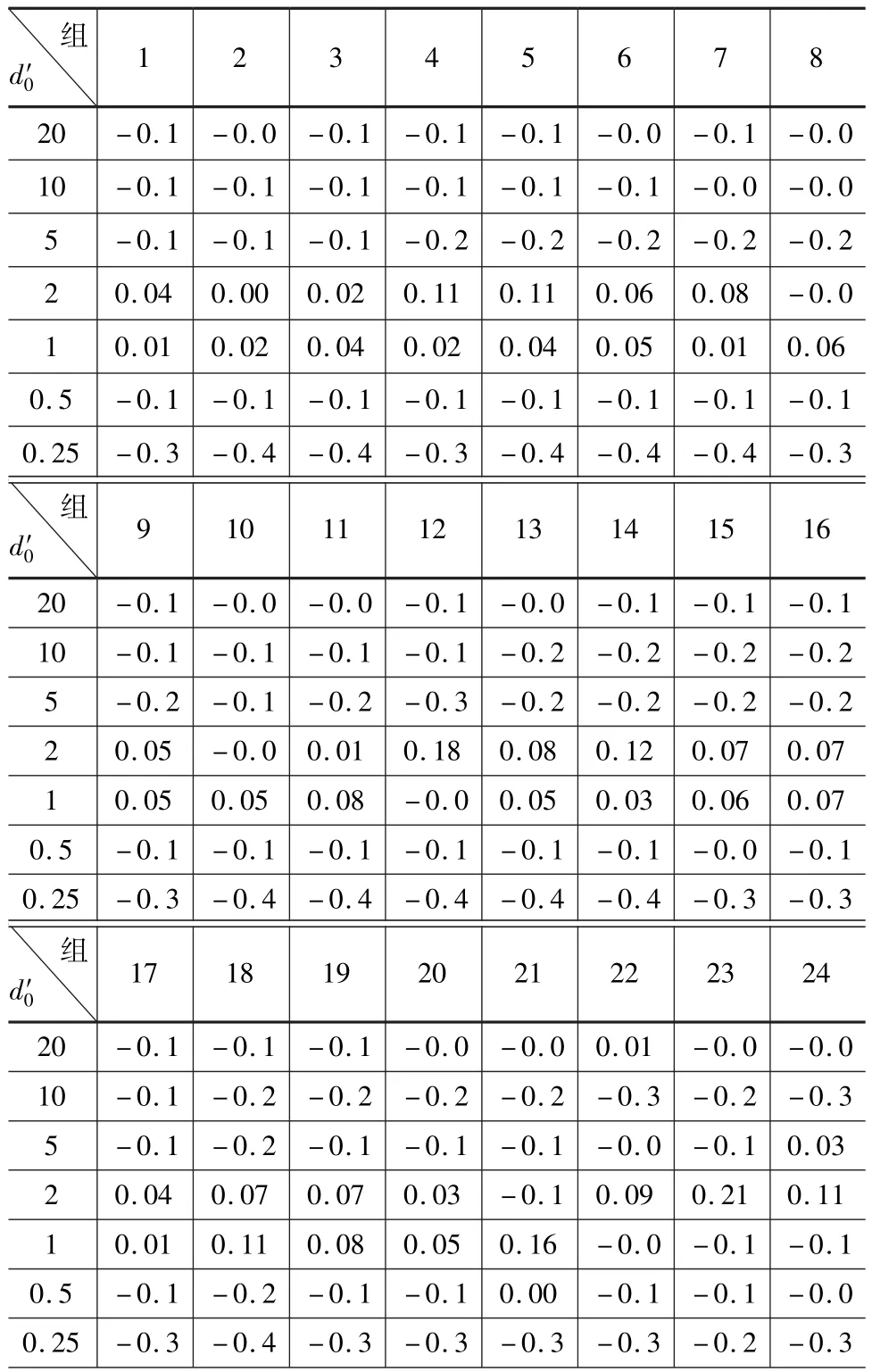
表4 各粒组对数线性插值数据偏差分析

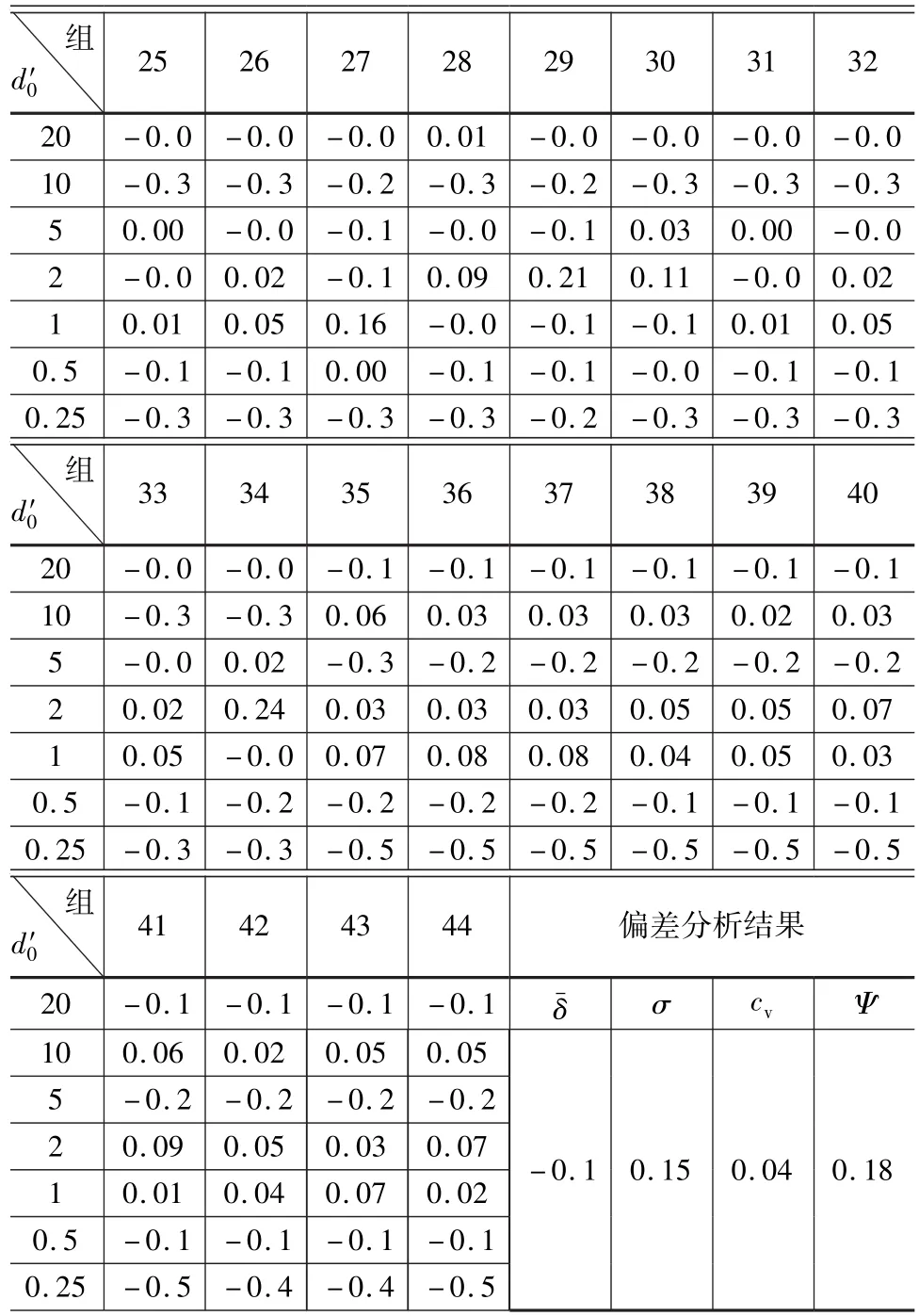
续表4

由表3和表4对照可知，对于同样的44组试验数据，除线性插值法的变异系数略大于对数线性插值法外，相对偏差均值、相对偏差标准差、偏差系数均大于线性对数插值法。由于偏差系数反映了插值偏差整体情况，因此对数线性插值精度优于对数插值[8－10]。

4.2 特征粒径推算

以表2中数据为例，计算d60、d30及曲率系数和不均匀系数。

由表中数据知，60∈(54.2，69)，d54.2＝10，d69＝20；30∈(25.5，33.6)，d25.5＝1，d33.6＝2。 试验中恰好测得d10＝0.25，则由式(2)可知:

故不均匀系数:Cu＝13.12/0.25＝52.5；Cc＝1.362/(13.12×0.25)＝0.56。

5 实用化程序

本方法虽较大程度提高了插值计算的可靠性，但计算过程偏繁琐。为适应工程中快速准确计算，为此利用CASIOfx-5800P可编程函数计算器编制通用计算程序，以满足现场数据记录和计算要求，程序源代码如下:

上述代码执行过程可实现如下功能:

(1)程序提供了“线性插值”和“对数线性插值”两种计算模式。

(2)一次性最多支持输入13组粒组数据。

(3)在任意指定质量百分比时，程序可根据输入的粒组数据自动搜索相邻的质量百分比及对应的特征粒径。

(4)只需一次性输入单次试验粒组数据后，可重复计算任意质量百分比的特征粒径，无需重复录入粒组数据。

(5)考虑土工筛分试验和数据记录的习惯，程序中粒组数据的录入按从大粒径向小粒径的顺序输入，且与计算结果唯一对应。若粒径录入顺序与之相反，则计算会出错[11－12]。

计算器程序编辑、运行界面如图3所示。

图3 计算器程序编辑及输出界面

6 结论

本文通过分析线性插值法和对数线性插值法两种方法的插值偏差，并通过大量样本数据进行验证，得到如下结论:

(1)重新定义的变异系数可有效解决数据数量级跨度较大、量纲不统一、均值趋于零一类样本离散特性难以评估的问题。

(2)构造了基于对数坐标线性插值的方法，提出的“跳点法”可有效评估各类插值方法偏差。

(3)构造的“偏差系数”综合考虑了均值、标准差、变异系数特性，可定量评估不同插值方法间的偏差大小，为在不同的样本条件下科学选取插值方法提供了依据。

(4)对数线性插值的偏差要小于线性插值偏差，且因实用化程序的提出，实际工程中建议尽量采用对数线性插值方法。