一种新的运营线路纵断面线形调整方法
2022-05-12陶佳元
陶佳元
(中铁上海设计院集团有限公司 上海 200070)
1 引言
高速铁路要求轨道具有高平顺性,但是由于线下工程变形、轨道结构病害、周边施工等因素影响,导致线路纵断面偏离原设计线位,产生轨道高低不平顺[1-5]。对于运营线路无砟轨道,可通过扣件调整、无砟轨道切割、道床注浆抬升[6]等方法使轨道恢复平顺状态。当线路纵断面调整受限无法恢复至设计线位时,则需要重新设计纵断面线形并验证其是否满足相关平顺性标准[7-9]。
轨道不平顺地段的纵断面调整通常采用线形重构方法[10],即根据实际测量数据,对各项参数进行合理选取,拟合优化新的纵断面。由于该调整方法基于“由线至点”的理念,故无法充分考虑局部地段(例如调整量受限地段)的约束条件。国内亦有学者提出了以轨面曲率[11]为控制指标的纵断面线形调整方法,但其“逐枕适算,反复迭代”的算法效率欠佳,且方案存在不收敛问题。鉴于此,本文提出了一种基于三次样条插值法的无砟轨道纵断面线形调整方法,将可调整量作为控制参数,能够快速有效地制定调整方案。
2 基于三次样条插值的纵断面线形调整方法及应用实例
钢轨是具有一定刚度的连续梁式结构,可以认为其纵向表面线是沿里程变化的光滑曲线。通过数值分析的方法,能够求得轨面高程与里程对应的函数关系,从而更准确地描述这条光滑曲线。本文采用三次样条插值法对纵断面曲线进行拟合。
2.1 三次样条插值原理
样条插值是使用特殊分段多项式进行插值的形式,可以通过低阶多项式样条实现较小的插值误差,工程应用中常选择三次多项式进行拟合。
三次样条插值定义:函数S(x)∈C2[a,b],在每个小区间[xj,xj+1]上均为三次多项式。其中a=x0<x1…<xn=b为给定节点,则:
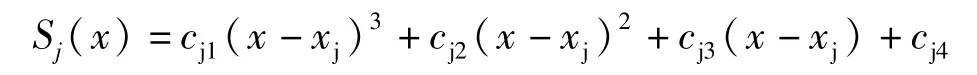
需要满足下列条件:
(1)插值特性
在节点xj上给定节点值yj:
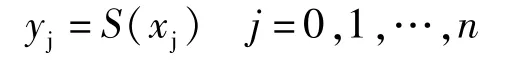
(2)样条相互连接
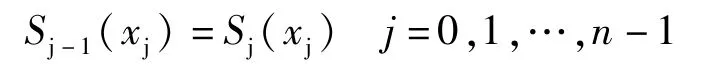
(3)两次连续可导

由于每个三次多项式需要四个条件才能确定曲线形状,所以对于组成样条函数的n个三次多项式,需要4n个条件才能确定多项式系数。但是,综上(1)~(3)仅给出(4n-2)个条件,因此还需要另外两个条件。根据实际纵断面高程曲线特性,取自然边界条件:S″(x0) =S″(xn) =0,从而求得各区间上的三次样条函数S(x)。
2.2 纵断面线形调整方法
与传统的“线形重构”“逐枕扫描”调整方法不同,本文所提出的基于三次样条插值的纵断面调整方法是根据若干扣件节点的里程(xj)以及与之对应的实测高程值(yj),构造纵断面三次样条曲线,通过与纵断面实测高程曲线对比,确定各扣件节点处的调整量。
2.2.1 简化及假设条件
为了清晰明确介绍本文所提出的纵断面线形调整方法,做以下简化及假设:
(1)目标对象为运营线路无砟轨道,轨面高程采用扣件进行调整。
(2)不考虑轨向、水平以及扭曲等不平顺影响,仅针对轨面高程进行调整。
(3)调整节点在调整后对其前后非调整节点位置的轨道几何尺寸无影响。
2.2.2 线形调整流程
基于三次样条插值的纵断面线形调整方法流程如图1所示。

图1 线形调整流程
(1)收集基础数据。基础数据包括调整范围内线路静态测量数据以及扣件调整储备量。
(2)确定基准节点。选择纵断面上若干绝对偏差量较大的“极值点”作为初始基准节点,并根据节点处扣件调整储备量设置实际调整量。
(3)构造三次样条曲线。根据所有基准节点调整后的高程数据及边界条件,对纵断面进行三次样条拟合,构造纵断面三次样条曲线,并由此计算各扣件节点处的调整量。
(4)迭代完善调整方案。若扣件节点处的调整需求不满足调整储备量,则将其选取为新的基准节点,并设置可实施的调整量;根据已有基准节点重新构造三次样条曲线,迭代循环至各扣件节点处调整量均满足要求,该调整方案即为最终方案。
由于引入了“基准节点”,基于三次样条插值的纵断面线形调整方法能够优先在绝对偏差量较大和调整量受限位置实施合理可行的调整方案,从而提高方案整体计算效率。同时,本文提出的调整方法结合了“由点成线”和“由线至点”的理念,使其能够兼顾方案的“局部”和“整体”,确保输出方案的可行性,实现快速有效地制定调整方案。
2.3 调整方法应用实例
以某铁路区间纵断面待调整地段(长度500 m)为例,采用本文所述方法制定调整方案,对其过程进行说明。该地段铺设无砟轨道,采用WJ-8B型扣件,垂向调整量理论值为[-4 mm,+26 mm]。
(1)收集调整地段无砟轨道轨面高程实测数据及扣件调整储备量数据。
(2)调整地段内共计800处扣件节点,根据实测轨面高程曲线确定初始基准节点,分别为第1号(起始节点)、第402号(高程偏差极值点)和第800号(终止节点)。
(3)第402号扣件节点处原始轨面高程偏差值为-39 mm,既有扣件调整量为0。故取调整量最大值+26 mm进行轨面高程调整,其余两处基准节点不设置调整量。根据以上三处基准节点对纵断面进行三次样条拟合,得到纵断面三次样条曲线并计算各扣件节点处所需调整量。
(4)遍历扣件节点所需调整量与实际调整储备量,第194号扣件节点不满足要求。该处计算调整量为-4 mm,由于该处已有-2 mm调整量,无法实现-4 mm的计算调整量,因此将该扣件设为基准节点,取可调整量最大值-2 mm进行轨面高程调整。根据以上4处基准节点重新拟合纵断面三次样条曲线并计算各扣件节点处所需调整量。
(5)遍历扣件节点所需调整量与实际调整储备量,第377号扣件节点不满足要求。该处计算调整量为+22 mm,由于该处已有+6 mm调整量,无法实现+22 mm的计算调整量,因此将该扣件设为基准节点,取可调整量最大值+20 mm进行轨面高程调整。根据以上5处基准节点重新拟合纵断面三次样条曲线并计算扣件节点处所需调整量。
(6)遍历扣件节点所需调整量与实际调整储备量,第474号扣件节点不满足要求。该处计算调整量为+25 mm,由于该处已有+2 mm调整量,无法实现+25 mm的计算调整量,因此将该扣件设为基准节点,取可调整量最大值+24 mm进行轨面高程调整。根据以上6处基准节点重新拟合纵断面三次样条曲线并计算各扣件节点处所需调整量。
(7)遍历扣件节点所需调整量与实际调整储备量,第763号扣件节点不满足要求。该处计算调整量为-5 mm,由于该处已有-2 mm调整量,无法实现-5 mm的计算调整量,因此将该扣件设为基准节点,取可调整量最大值-2 mm进行轨面高程调整。根据以上7处基准节点重新拟合纵断面三次样条曲线并计算各扣件节点处所需调整量。
(8)遍历扣件节点所需调整量与实际调整储备量,各扣件节点均满足要求,调整量计算结束。
综上所述,根据初始基准节点首次拟合纵断面三次样条曲线后,历经4次迭代即可输出最终调整方案。调整前、后纵断面如图2所示。

图2 纵断面调整前、后对比
3 调整方案评价
上述应用实例体现了本文所述调整方法的便利性,本节将从平顺性指标、轨面曲率以及车辆-轨道动力学响应三方面对其有效性进行评价。
3.1 平顺性指标
根据《高速铁路无砟轨道线路维修规则(试行)》,一般采用以下三项静态指标对高低不平顺进行控制:10 m弦的正矢差;30 m弦长相隔为5 m的测点实际矢高差与设计矢高差的差值;300 m弦长相隔为150 m的测点实际矢高差与设计矢高差的差值。各项平顺性指标的允许偏差见表1。

表1 平顺性指标允许偏差
对调整前后的轨道高低平顺性指标进行计算,计算结果如图3~图5所示。

图3 调整前后10 m弦正矢差波形及分布直方图

图4 调整前后30 m弦长相隔为5 m的测点实际矢高差与设计矢高差的差值波形及分布直方图
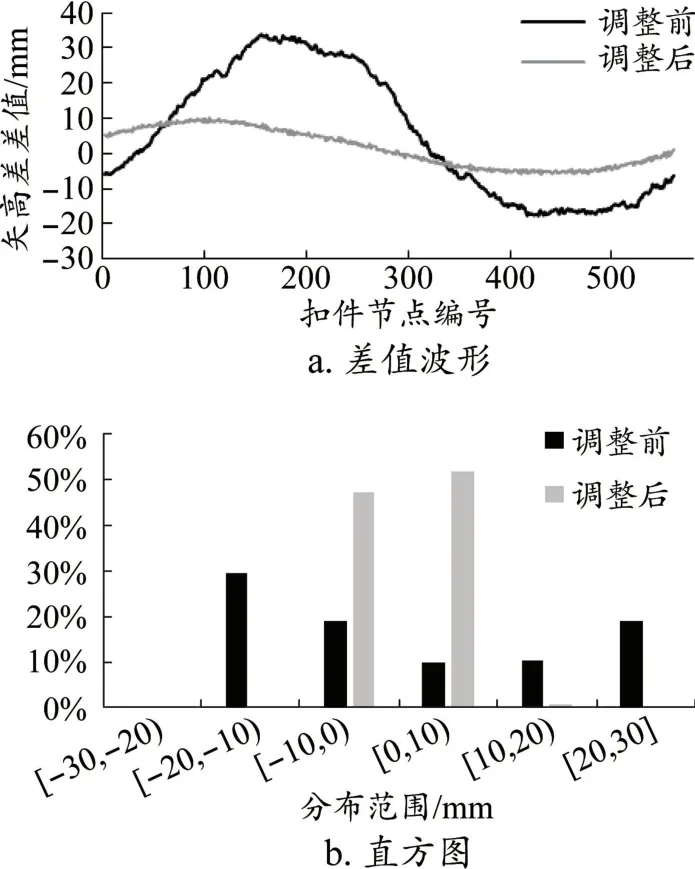
图5 调整前后300 m弦长相隔为150 m的测点实际矢高差与设计矢高差的差值波形及分布直方图
由图3~至图5可以看出,轨面高程调整后各平顺性指标均有不同程度改善:10 m弦长和30 m弦长两项指标的幅值均控制在[-1 mm,+1 mm]范围内,满足允许偏差要求;300 m弦长指标的最大值由调整前的34 mm下降为调整后的10 mm,满足允许偏差要求。300 m弦长指标改善效果明显,体现了基于三次样条插值的调整方法对于存在幅值较大的长波高低不平顺情况下轨面高程调整的适用性。
3.2 轨面曲率
轨面曲率表示轨面高程曲线的弯曲程度,可以从一定程度上反映出轨面的平顺性。以各承轨台作为节点,对轨面高程曲线进行三次样条插值,将其离散为一连串三次多项式后,即可以通过公式k=(y″)/(1+y′2)3/2计算得到各扣件节点处的轨面曲率。调整后轨面曲率如图6所示。由于采用了基于三次样条插值的调整方法,因此纵断面线形曲率呈线性变化,从而避免了曲率突变对轮轨接触状态造成的不利影响。
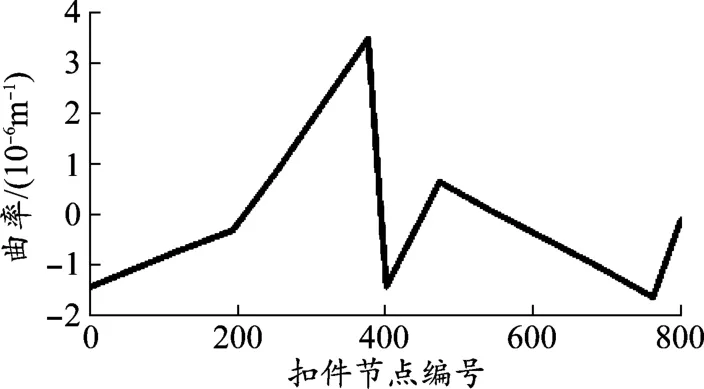
图6 轨面曲率
3.3 车辆-轨道动力学响应
在轮轨动力学和多体动力学理论的基础上,采用多体动力学仿真分析软件建立CRH380A型动车模型[12],并将轨面高程作为左右轨高低不平顺数据,对调整前后的车辆-轨道动力学响应进行仿真计算,以此检验轨面不平顺的改善程度。列车运行速度为350 km/h,仿真计算结果见表2。
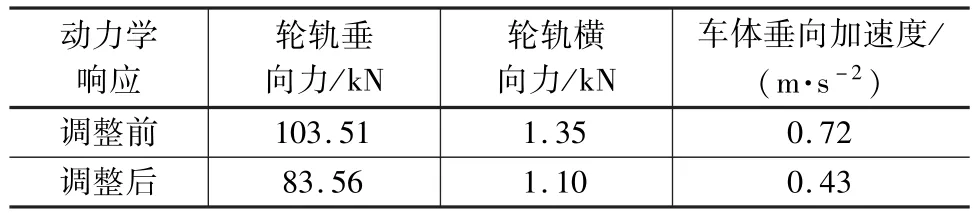
表2 调整前后各项响应最大值对比
4 结束语
针对已运营线路轨道出现高低不平顺,仅调整受限纵断面无法恢复至设计线位情况,提出了基于三次样条插值的纵断面线形调整方法,并结合实际案例开展应用研究,对所制定的调整方案进行了评价,结果表明:
(1)基于三次样条插值的纵断面线形调整方法可针对线路实际情况快速制定合理可行的调整方案。
(2)纵断面调整后,各平顺性指标均满足规范要求,300 m弦长指标的最大值由调整前的34 mm下降为调整后的10 mm,改善效果明显。
(3)纵断面调整后,轨面曲率幅值较小,且呈线性变化,避免了轨面曲率突变对轮轨接触状态的不利影响。
(4)纵断面调整后,轮轨垂向力、轮轨横向力以及车体垂向加速度等动力学响应指标均有所减小。
