大空隙透水铺装基层碎石抗压碎性能的试验和计算

2022-08-30徐钰鹏刘建石何会新夏邵君兰小磊

南京航空航天大学学报 2022年4期

徐钰鹏，刘建石，何会新，王强，夏邵君，兰小磊，耿飞

（1.南京航空航天大学民航学院，南京 211106；2.南京安居保障房建设发展有限公司，南京 211199；3.中交第四公路工程局有限公司，北京 100022）

级配碎石常用于低交通量道路的基层，或是重载交通道路的垫层，由于其强度偏低，在工程设计上常采用骨架密实型级配［1-2］。近几年来随着轻、中荷载透水路面的应用，传统的骨架密实型级配碎石本身虽可满足一定的渗透要求，但在路面雨水汇流较大时，往往会形成雨水滞留，造成城市内涝，增加碎石空隙率是提高路面基层渗透性能的有效措施。传统的级配基层仅以抗剪强度、回弹模量、永久变形和加州承载比（California bearing ratio，CBR）作为其主要控制指标［3-8］，然而随着级配碎石空隙率的增大，其压碎值不合格的概率也越大，此概率又与级配有较大关系［9］，而目前针对大空隙级配碎石压碎值的研究较少［10］，级配碎石压碎值计算模型研究也几乎处于空白状态，为满足空隙率与压碎值要求而一味选用强度较大的碎石会提高工程的造价。

本文对不同空隙率与粒级碎石的压碎值进行了试验，研究了级配对饱水和干燥状态下压碎值的影响；基于压碎前后粒径含量的变化规律分析了压碎值变化机理，设计了相关计算模型，旨在探究压碎值与级配组成之间的关系，为轻、中荷载透水路面大空隙级配碎石基层的设计提供参考。

1 试验概况

1.1 试验材料

所用碎石为石灰岩碎石，其压碎值、针片状颗粒、软弱颗粒、杂质含量等指标符合《城镇道路工程施工与质量验收规范》CJJ1—2008 中的要求；所用砂为天然河砂，其含泥量、泥块、云母和轻物质含量等指标符合标准《建设用砂》GB/T14684—2011 中I 类砂的要求。

1.2 试验级配

参考《透水砖路面技术规程》CJJ/T188—2012，级配碎石基层的最大粒径选用26.5 mm。为满足路面基层的渗透要求，级配碎石空隙率不得低于13%［11］，试验选用25%、30% 和35%，分别记作SU-25%、SU-30%和SU-35%；通过在碎石中掺加一定量1.18～2.36 mm 的砂形成砂石级配，模拟基层空隙堵塞的工况，空隙率选用25%、30% 和35%，分别记作SH-25%、SH-30%和SH-35%；设计3 种单粒级碎石级配作为补充，分别记作DA-Ⅰ、DA-Ⅱ和DA-Ⅲ。采用体积设计法进行目标空隙率的连续级配设计［11］，具体级配如表1所示。

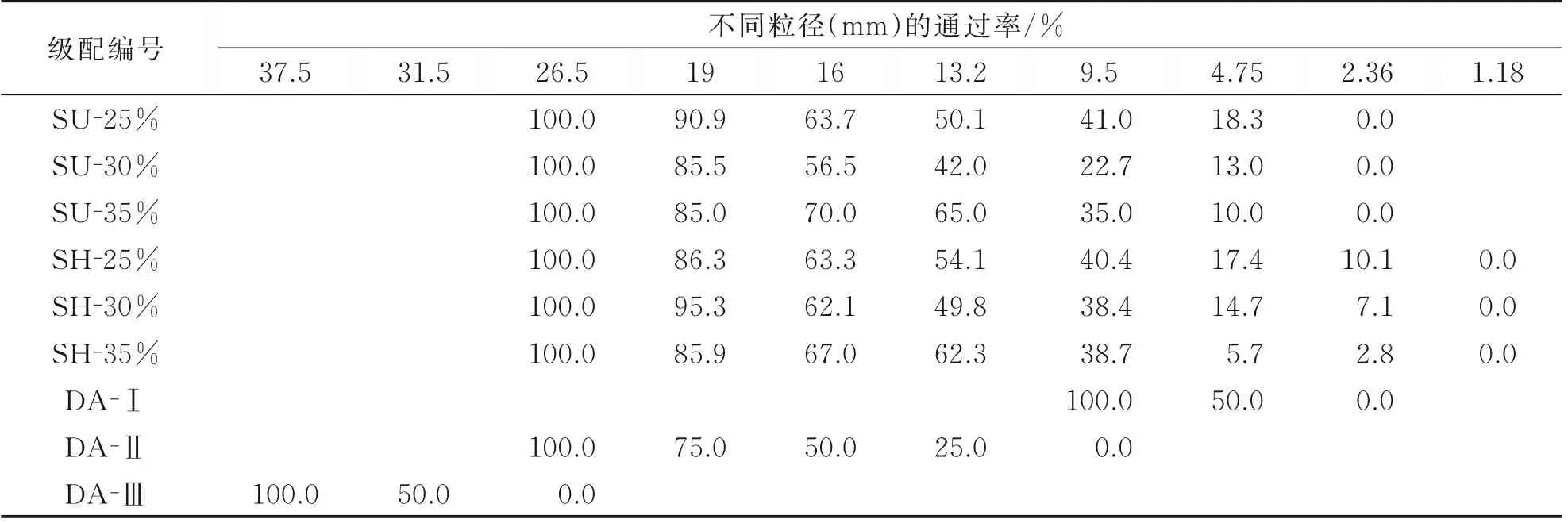
表1 碎石级配通过率Table 1 Passing rate of graded gravel

1.3 试验方法

试验参考《公路工程集料试验规程》JTGE42—2005 中的压碎值试验方法进行，对部分操作步骤做了调整：（1）每组试样直接称取3.5 kg；（2）2.36 mm 以下粉料量用试样总量减去2.36 mm 筛余得到；（3）试验测试SU 组和SH 组的饱水压碎值，浸水处理24 h，水需浸没试样顶部5 cm，压碎后在70 ℃下烘烤12 h 后再进行称料；（4）SH 组压碎后2.36 mm 筛孔的通过质量需扣除砂的初始质量。

2 试验结果与分析

2.1 级配对饱水压碎值的影响

试验结果如表2 所示，可以看出：（1）SU 组在饱水24 h 后压碎值略有升高，平均升高幅度约0.63%。压碎值增加量SU-25%＞SU-30%＞SU-35%，这是由于3 种级配中2.36～4.75 mm 细集料含量SU-25%＞SU-30%＞SU-35%，细集料的比表面积更大，软化效率更高。（2）SH 组在饱水24 h 后压碎值略有下降，平均下降幅度在0.37%。这是因为水将砂粘结在一起，应力集中现象减少，且细砂的滚珠轴承作用在饱水后更加明显，碎石在受压时更容易通过滑动调整位置，形成一个相对更好的受力结构。

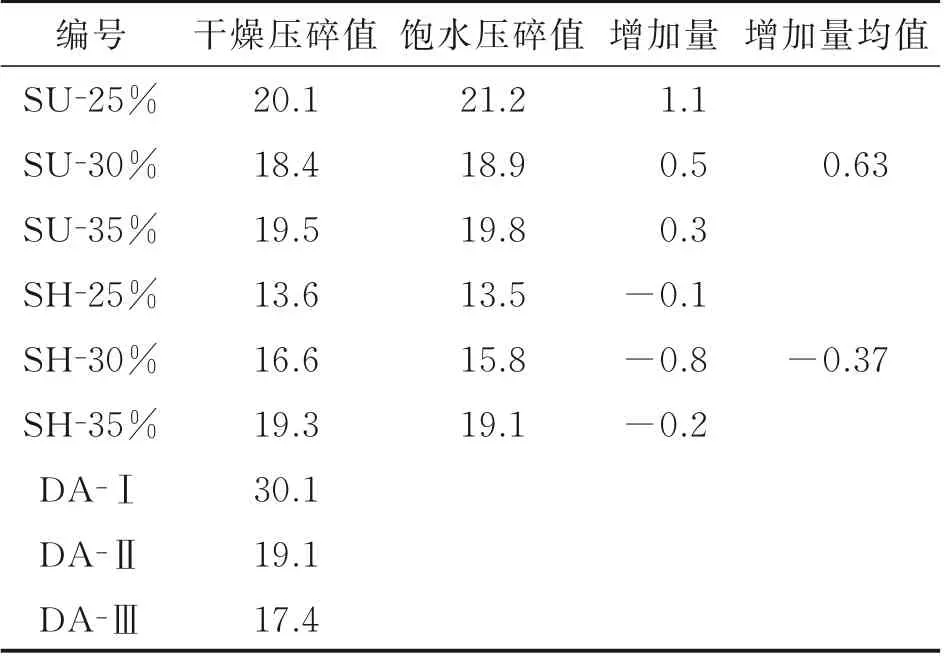
表2 碎石压碎值试验结果Table 2 Test results for crushing value of gravel %

图1 为SH 组干燥与饱水状态下压碎断面对比，干燥组中的砂几乎覆盖了整个断面，大量的砂存在于骨料与骨料中间，加剧了应力集中现象；而饱水组中的砂分布面积较小，集中在骨架空隙中，有利于结构整体受力。SH-30% 的砂含量处于SH-25%与SH-35%之间，但其饱水后压碎值减少最多，这是因为过多的砂不利于应力集中的减少，过少的砂不利于滚珠轴承效果的加强。

图1 SH 组干燥和饱水状态下压碎值试验断面Fig.1 Sections of test specimens for crushing value of SH in dry and saturated states

2.2 级配对干燥压碎值的影响

2.2.1 粒径含量变化分析

对级配碎石压碎前后各粒径含量变化率进行计算，具体见图2。由于SU-35% 和SH-35% 的13.2～16 mm 粒径含量分别只占5.0%和4.7%，故将其与9.5～13.2 mm 粒径合并考虑。原有粒径计算在原含量基础上的变化率，新增粒径（如SU 组2.36 mm 以下的粉料、SH 组1.18 mm 以下的粉料）是由其他所有粒径压碎后产生的，其变化率按占总料的百分比计。

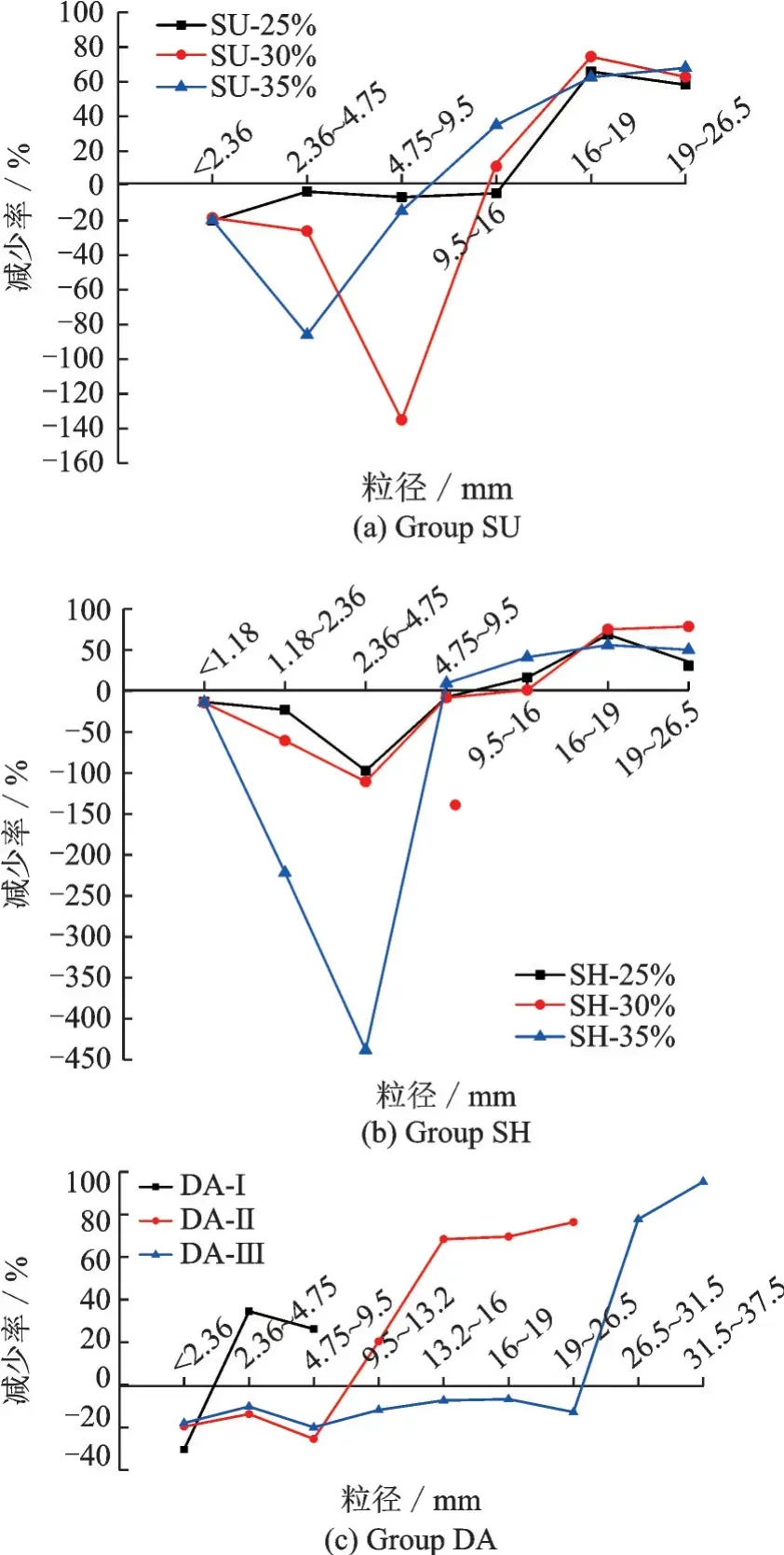
图2 不同级配压碎前后各粒径含量减少率Fig.2 Reduction rate of content of the gravel’s each particle size part with different gradations after crushing compared with before

对图2 进行分析，发现不同级配中粒径较大的碎石其含量减少率普遍更大，且DA 组3 种最大粒径4.75～9.5 mm、19～26.5 mm 和31.5～37.5 mm压碎后的减少率存在明显的梯度（分别为26.2%、76.4%和95.4%），可以认为大粒径碎石总是首先承担荷载而被压碎，因此级配中的最大粒径越大、较大粒径含量越多，则压碎值越小；DA 组压碎值，DA-Ⅱ比DA-Ⅰ低11.0%，而DA-Ⅲ仅比DA-Ⅱ低1.7%，随着粒径的增大，粒径对压碎值的减小效果逐渐降低，故级配碎石最大粒径在19～26.5 mm 较为适宜。

2.2.2 压碎值回归分析

将具有应力集中和滚珠轴承作用的2.36 mm以下砂的含量和主要承受荷载的9.5 mm 以上碎石的含量分别与压碎值进行对比分析，如表3 所示。SU 组的压碎值与9.5 mm 以上碎石含量有着很好的线性关系，回归方程为式（1），利用该式对SU组、SH 组和DA 组压碎值进行计算，结果列入表3。

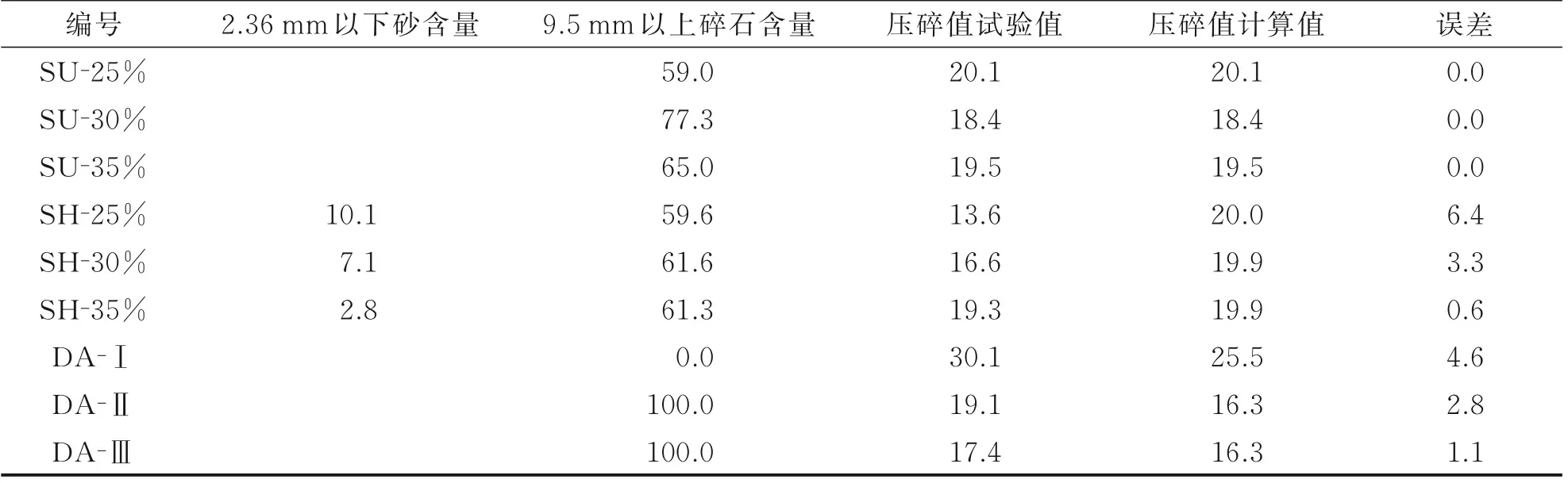
表3 基于2.36 mm 以下砂含量和9.5 mm 以上碎石含量的压碎值分析与计算Table 3 Analysis and calculation of crushing value based on content of gravel with the size smaller than 2.36 mm andgreater than 9.5 mm %

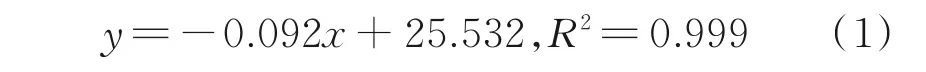
SH 组压碎值不符合式（1），且与大粒径含量无明显关系，但在9.5 mm 以上的碎石含量接近时（59.6%～61.6%），其压碎值与砂含量具有较好的线性关系，回归方程如下

y=0.77x-21.635，x∈(0.0，10.0)，R2=0.982（2）

根据式（2），当9.5 mm 以上的碎石组成的骨架形成后，细砂含量在0.0～10.0% 之间每增加1.0%，压碎值将减小0.77%，这显然与事实不符。究其原因，砂不参与骨架结构的组成，不会被压碎，将压碎值作为砂石的抗压碎能力评价指标并不适宜（但可用来判断砂石饱水前后抗压碎能力的变化），建议将压碎值代之以9.5 mm 以上碎石含量。

DA 组压碎值同样不符合式（1），为进一步研究级配对大空隙碎石压碎值的影响，完善相关计算模型，需要对碎石压碎前后的粒径含量变化展开进一步分析。

3 压碎值变化机理分析与计算

3.1 临界粒径理论

基于图2 对级配碎石压碎后含量增幅最大的粒径（以下简称临界粒径）与9.5 mm 以上粒径含量进行对比分析，如图3 所示。当9.5 mm 以上粒径含量从0 单调增加到100%时，临界粒径范围从＜2.36 mm 单调增加到4.75～9.50 mm，据此提出压碎值的“临界粒径理论”：（1）粒径大于9.5 mm 的碎石压碎后，临界粒径位于2.36 mm 以上，且随着粒径和大粒径含量的增加而增大，并如图2（a，b）以类正态峰值的形式逐渐远离2.36 mm，压碎值逐渐减小；（2）粒径小于9.5 mm 的碎石压碎后，临界粒径位于2.36 mm 以下，如图2（c）DA-Ⅰ所示，此时随着大粒径含量的增加，碎石压碎后2.36 mm 以下颗粒的增加量也随之增加，压碎值逐渐增大；（3）粒径等于9.5 mm 的碎石压碎后，临界粒径约等于2.36 mm。

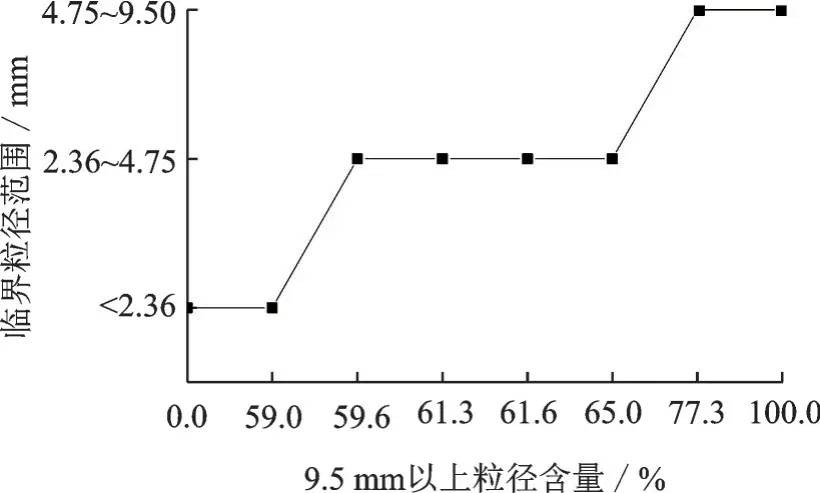
图3 各级配的临界粒径范围与9.5 mm 以上粒径含量对比Fig.3 Comparison of range of critical particle size and content of gravel with a particle size greater than 9.5 mm

令9.5 mm 以上和以下的碎石分别为A 部分和B 部分，基于上述理论可以得出推论：任意级配的B 部分含量占比可调整至一个值（以下简称临界占比），该值在该级配下是唯一的，使得A 对临界粒径的增大效果与B 对临界粒径的减小效果抵消，此时临界粒径刚好为2.36 mm。

当级配变化时，即使A 和B 占比恒定，其对临界粒径的减小和增大效果也是不同的，故不同级配存在不同的临界占比。为验证推论的正确性，提出“临界占比假设”：当采用连续级配、粒径范围较小且相近时，认为不同级配的临界占比较为接近。基于该假设对SU 组与SH 组进行分析，只有SU-25%的临界粒径在2.36 mm 以下，而其9.5 mm以上碎石含量也为最小的59.0%，其次为SH-25%的59.6%，相应的，SH-25%的2.36～4.75 mm 粒径增量仅比2.36 mm 以下粒径增量略大一点。可以得出粒径范围2.36～26.5 mm 的连续级配的临界占比真实存在且在59.0%～59.6%之间，这一定程度上证实了推论的正确性。基于此，本文提出该粒径范围内的大空隙连续级配应将9.5 mm 以上碎石含量控制在59.6%以上，可有效避免临界粒径出现在2.36 mm 以下，进而降低大空隙级配碎石的压碎值。

3.2 计算模型设计

根据“临界粒径理论”对大空隙级配碎石的压碎值进行计算，其中所述“大粒径”为相对概念，其下限粒径（以下简称分界粒径）由加权平均粒径决定，至此提出压碎值的“分界粒径假设”：（1）当分界粒径大于9.5 mm，此时压碎值由大粒径主导，9.5 mm 以下集料对压碎值的增大作用及9.5 mm和分界粒径之间的集料对压碎值的减小作用可以忽略，但需要考虑细（相对）集料填充作用对压碎值的降低效果；（2）当分界粒径小于9.5 mm，此时需要考虑9.5 mm 以上集料对压碎值的减小作用以及分界粒径和9.5 mm 之间的集料对压碎值的增大作用，分界粒径以下集料对压碎值的增大作用可以忽略。基于上述“理论”“推论”和“假设”，对式（1）改进如下

式中：Q为压碎值，%；dboundary为分界粒径，mm；c为基于大粒径含量的计算系数，%；xk为第k挡粒径的碎石含量，%；dkmax为第k挡粒径区间内的最大粒径，mm；dkmin为第k挡粒径区间内的最小粒径，mm；Dk为第k挡粒径区间的平均粒径，mm；ak为第k挡粒径折减系数。

a、D、x、d的下标k代表不同的粒径区间，按表4 依次取值。其中i为以分界粒径dboundary为最小粒径的粒径区间所在挡数，j为以不大于0.22dnmax且距0.22dnmax最近的筛孔尺寸为最大粒径的粒径区间所在挡数。

表4 a、D 和x 的下标k 取值Table 4 Subscript k of a,D and x

式（3～8）适用于不具有单一粒径特征的碎石连续级配、间断级配和单粒级级配，且最小粒径不小于2.36 mm，这是因为：（1）公式利用级配中较大粒径和填充粒径的碎石对压碎值的影响进行压碎值计算，故无法计算单一粒径碎石压碎值；（2）粒径小于2.36 mm 的砂不会被压碎，会对压碎值起到干扰作用。贝雷法认为，次一级填充集料的最大粒径为上一级的0.22 倍，故0.22dnmax以下的碎石作填充作用［12］，函数f(x1，x2，…，xj)考虑了小粒径碎石的骨架填充作用对压碎值的改善，但其具体表达式还未能确定，当0.22dnmax以下碎石含量小于20%时，f(x1，x2，…，xj)近似按0 处理。

式（1）中自变量最大为100.0，因此该式无法计算小于16.332 的压碎值，根据彭秋乐［12］的试验结果，当碎石粒径大于13.2 时，压碎值小于16.332，因此通过式（7）将大于13.2 mm 的粒径含量化为等价的9.5～13.2 mm 粒径含量。由于碎石粒径越大，对压碎值的减小效果越低，因此粒径含量转化时需要乘以折减系数ak。根据SU-25%、SU-30% 和SU-35%的压碎值，利用式（3～8）反算X1，计算结果精确到小数点后三位并填入表5。

表5 X1 与Dk xk 的回归分析Table 5 Regression analysis of X1 and Dkxk

将X1与Dk xk进行回归分析，根据式（4）建立式（9）的多元线性回归模型，回归分析结果如表6所示。

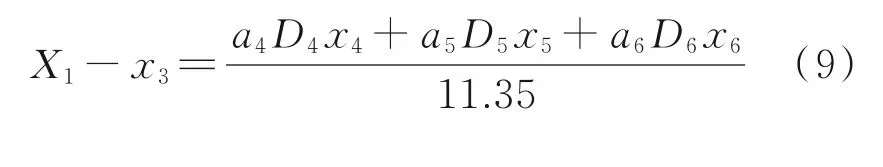
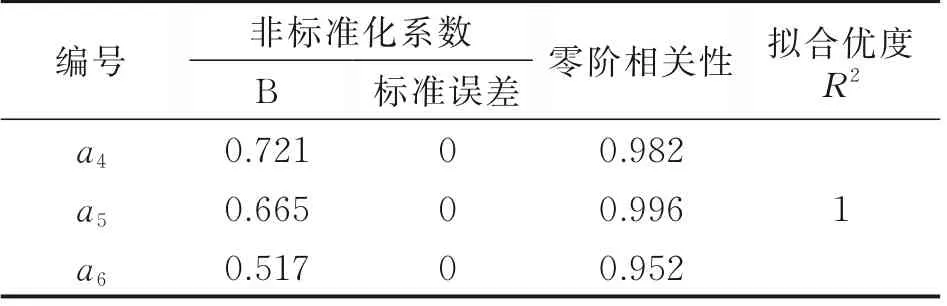
表6 折减系数的多元线性回归结果Table 6 Multiple linear regression results of reduction coefficients

对a4进行修正，当9.5～13.2 mm 和13.2～16 mm 两挡粒径混合，设后者粒径含量为x%，按式（7）计算X1，建立函数X1(x)。结合式（3）发现X1(x)为单调增函数，a4应大于0.777，根据彭秋乐［12］压碎值试验结果，反算出a4的均值为0.827。为避免扩大误差，仅对a4进行修正。

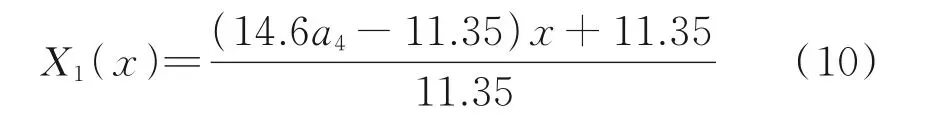
基于表7 中折减系数的原始值和区间平均粒径进行回归分析，综合考虑拟合优度和实际情况（回归方程在(9.5，+∞)上单调减，且函数值大于0），实际折减系数按式（11）计算，部分结果填入表7 中作为折减系数的计算值，并基于该值按式（12）和式（13）计算100 份大粒径集料的转化量Nk与粒径转化效率Ek。可以看出，粒径转化效率随粒径增大而减小，与试验结果一致。

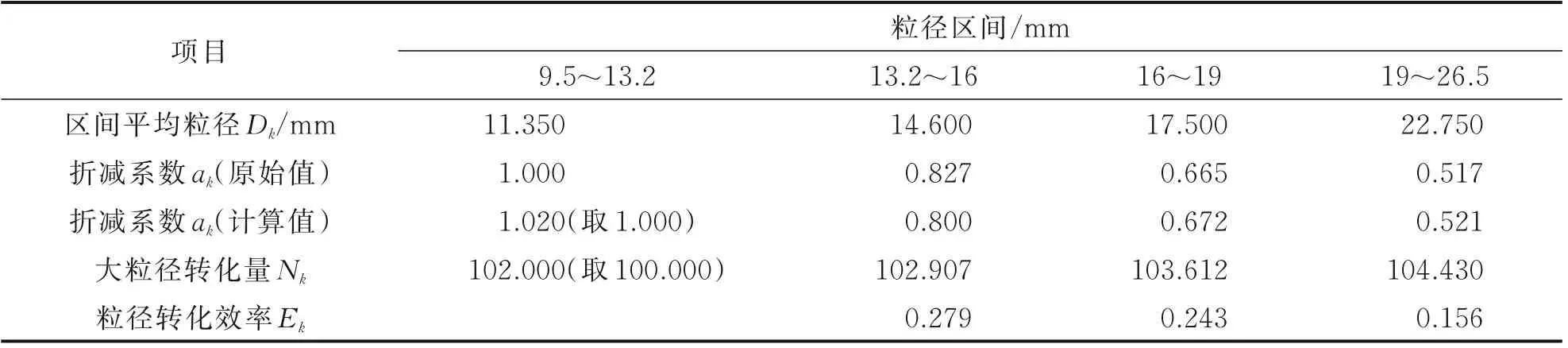
表7 粒径转化相关参数（部分）Table 7 Parameters related to the conversion of gravel content (part)

3.3 公式校核

利用式（3～8，11）对SU 组、DA 组及彭秋乐［12］和李晓燕［9］的试验压碎值进行计算校核，如表8 和表9 所示。彭秋乐的石灰岩碎石和李晓燕的花岗岩碎石压碎值计算校核平均误差分别为1.8%和2.4%（由于破碎作用、切割操作和颗粒形状等因素影响，天然骨料的母岩强度与压碎值的关系并不明显［13-14］，故不对花岗岩压碎值计算结果进行修正），碎石中针片状含量在0～25%之间时压碎值存在0～2.9%的偏差［12］，因此计算结果具有一定的精确度。花岗岩碎石压碎值计算结果误差略大，这是因为部分组别dboundary的取值存在偏差（如级配17、18和19 等），级配8 与级配11 计算值相差较大也是同样的原因。因此，式（4）中的系数0.77 还需进一步修正，其取值应考虑岩石种类、级配和粒径范围等多方面因素。

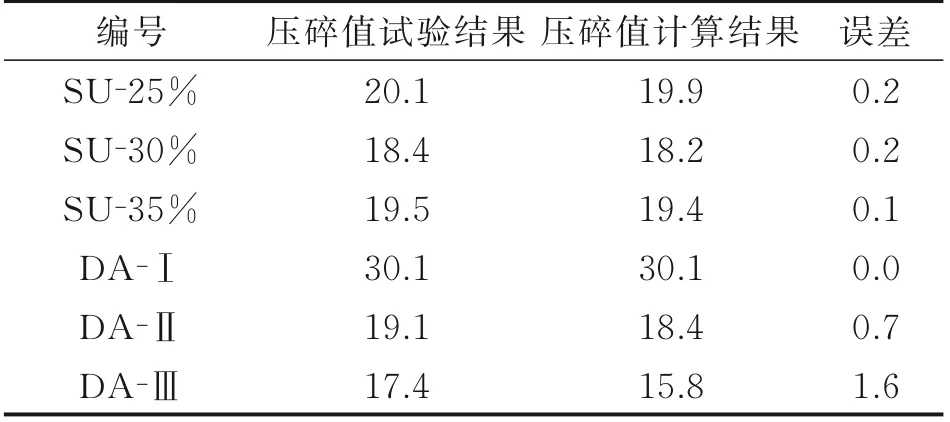
表8 SU 组、DA 组压碎值试验结果计算校核Table 8 Calculation and check for test results of group SU and group DA %

李晓燕［9］通过对表9 中级配16～51 进行分析，发现9.5 mm 以下粒径含量大于45.0%时，压碎值急剧增大至27.0%～29.0%，即9.5 mm 以上粒径含量应控制在55.0%以上，其认为9.5 mm 以下粒径含量对级配碎石压碎值与骨架结构有较大影响，但未能展开进一步分析。本文3.1 节得到了相近的结论并对此做出了较好的解释。

表9 对文献[12]中的石灰岩碎石、文献[9]中的花岗岩碎石压碎值试验结果计算校核Table 9 Calculation and check for test results in Ref.[12]with limestone and Ref.[9]with granite %

当采用再生骨料等特殊骨料时，上述计算公式存在两个重要问题：（1）9.5 mm 粒径的骨料压碎后，临界粒径不一定在2.36 mm 附近；（2）骨料压碎值等于16.332%时，其粒径不一定在13.2 mm 附近。为解决该问题，基于上述计算模型形成了专利“一种基于级配的多挡粒径碎石压碎值估算方法”，申请号202011148408.5，该专利考虑了不同碎石材料自身属性对压碎值的影响，具有更高的计算准确度和更广泛的应用价值。