4-SPS/UPU 并联机构运动学分析

朱东升，郭忠峰，赵文增

与六自由度并联机构相比，少自由度机构包含的元件较少，结构简单且紧凑，同时具备运动平稳、承载能力大和可控性能好等优点。因此，其发展前景相当好，从事这方面研究的人数也逐年增多[1～2]，如今被广泛应用在机床、医疗机器人、航天、微型操作等领域[3]。

少自由度并联机构中包括一种五自由度并联机构，该机构可分为两种运动情况，分别为三平移两转动和三转动两平移。唐卫星等[4]基于拓扑结构理论，全面系统地分析三平移两转动构型模型，并借助仿真软件证明模型的正确性。王劲松等[5]基于零位形两步法研究4-SPS-RRTR 并联机构用作实时位置控制的运动学反解，这种机构可应用在推拿机器人方面。王庚祥[6]等研究了五自由度的构型模型，分析了运动学的正反解，得到Jacobian 和Hessian 矩阵。陈修龙等[7]研究了 构型，通过引用平方平均灵巧度系数，对其运动性能进行全方位探讨后，得出最优的构型参数。O.Piccin 等[8]提出一个可应用在医疗手术定位方面的并联机器人模型，并推导出该模型的正逆运动学，以及符合实际的装配方式。郑魁敬等[9]研究5 自由度并联机床运动控制算法，编制系统控制软件，实现了对机床刀具位置姿态的控制。曹毅等[10]基于螺旋理论研究了3R2T 构型的运动状况并提出一种解耦方案，并验证其正确性。

基于以上研究背景，本文对一种五自由度的4-SPS/UPU 并联机构模型进行研究。

1 4-SPS/UPU 并联机构结构特点

4-SPS/UPU 并联机构的构型搭配结构的驱动支链由4 个分支SPS 组成，恰约束主动支链由UPU组成[11]（见图1）。4 个驱动分支中每一个都含有1 个移动副与2 个球副，其中各个分支都从上平台开始，第一运动副、第二运动副和第三运动副依次分别为球面副（S）、移动副（P） 和球面副；约束支链依次为万向铰（U）、移动副和万向铰，其中两个万向铰中心分别处在上、下平台的原点位置。在定平台上建立定系和动平台上建立动系。其中O 点位于下平台中心，P 点位于上平台中心，上、下平台是正方形分布，正方形边长分别为2a 和2b。与上平台连接在一起的驱动分支S 副质点为Ai，与下平台连接的S 副质心坐标为Bi；X 轴和Y 轴分别平行于B2B3与B3B4，Z 轴与下平台是垂直关系；动系的x 轴和y 轴分别平行于A2A3与A3A4，z 轴与上平台为垂直关系（见图1）。

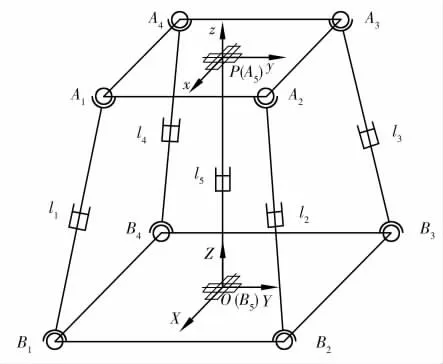
图1 4-SPS/UPU 并联机构结构简图

2 并联机构自由度分析计算

笔者采用螺旋理论求解4-SPS/UPU 机构的自由度。

首先对驱动支链进行分析，由于四条驱动分支结构相同，只需分析其中的一条支链即可得到四条支链的特点。下面挑选出一条支链进行旋量讨论（见图2）。

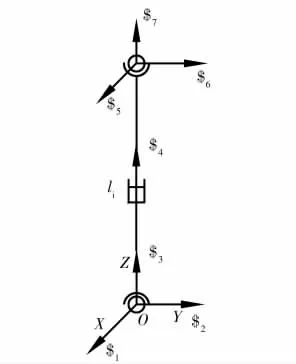
图2 SPS 支链旋量图

四条支链运动旋量表示为

由互易积：$ij·$r=0 可知，该线性方程组无解，即$r不存在，进而得知该螺旋系对运动平台没有出现任一方面的限制。所以该支链分支的自由度为6，也没有任何公共约束，即d=6。

由以上分析可知，该机构仅限制绕Z 轴方向的转动，所以该并联机构自由度为5。即动平台具有三移动和绕X 轴和Y 轴的两转动。

3 4-SPS/UPU 并联机构运动学分析

3.1 4-SPS/UPU 并联机构位置分析

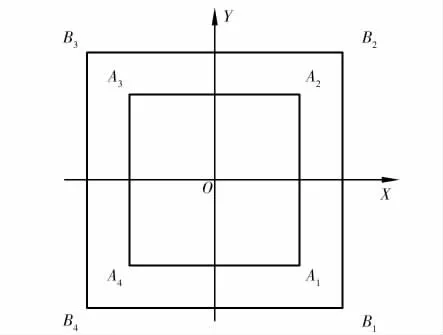
图3 4-SPS/UPU 并联机构鸟瞰简图

位置反解与正解是对立关系，位置反解是已知动平台的运动参数（x，y，z，α，β） 进而去求驱动杆的杆长范围；而位置正解是已得到构型基本参数和驱动杆（l1，l2，l3，l4，l5） 的变化范围，求解动平台的位姿（x，y，z，α，β）。

3.2 4-SPS/UPU 并联机构的速度分析

3.3 4-SPS/UPU 并联机构的加速度分析

借助式（10） 和（11），就能求出4-SPS/UPU 机构的加速度正解及逆解。

4 工作空间分析

并联机构的工作空间是指机构动平台末端执行器可运行到的所有工作范围；工作空间所构成的体积大小作为其性能的一个重要考虑内容，也从某一方面反应该机构的执行能力。

工作空间可划分为位置和姿态工作空间，对于超过3 自由度的并联机构，由于借助编程软件无法将全部参数在坐标系中表示，所以采取降维处理方式使得位姿可视化。

另外，关于工作空间约束除了上面算出的位置方程之外，还包括杆长、运动副角度和干涉约束。

笔者将驱动支链li（i=1，2，3，4） 单位向量分别定义为φ1，φ2，φ3，φ4，φ5，向量npi为动平台运动副基座在动系{p} 的姿态，向量nsi为静平台运动副基座在静系{O} 的姿态。得到并联机构具体的约束（见图4）。

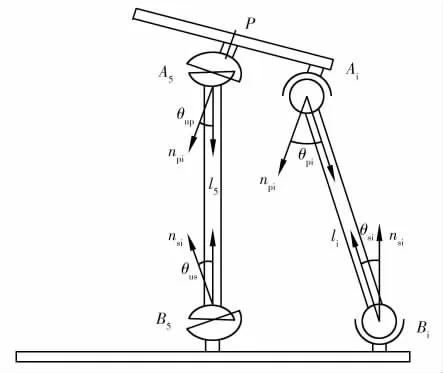
图4 4-SPS/UPU 关节的转角约束

（1） 杆长限制

由于并联机构中与上、下平台连接的各个杆分布比较分散，如果杆不发生干涉就不予考虑。

通过联立式（10） ～（17） 与位置约束式（7），满足所有符合约束条件的全部点所组成的体积就是这个机构的工作空间。

机构的结构参数如下：a=0.18 m，b=0.3 m；分别取：limin=0.4 m，limax=0.6，θsmax=35°，θumax=35°。当给定位置α=0°和β=0°时，即可求出工作空间（见图5）。由图可知，该位置空间分布规则且没有空洞，整体呈球柱体形状，符合该机构的特性。

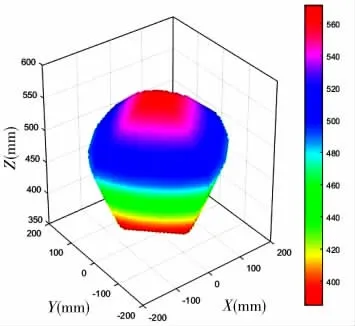
图5 4-SPS/UPU 并联机构工作空间

5 结 语

（1） 采用螺旋理论分析验证4-SPS/UPU 构型的自由度。通过运动学分析，构建出位置方程，研究4-SPS/UPU 并联机器人模型的速度和加速度的求解方法，得到了Jacobian 矩阵。

（2） 根据机构的逆运动求解方程及关节约束条件，计算定姿态下机构的工作空间，为其后续动力学、运动控制及应用提供参考。