基于UG 的球面渐开线弧齿锥齿轮参数化建模

许跃跃，王赫莹，郭忠峰，赵文增

螺旋锥齿轮是一种齿面节线为曲线的特殊构型的锥齿轮，螺旋锥齿轮有着不同标准的分类，通常按照其齿面节线形式的不同可以分为三类：圆弧齿锥齿轮、延伸外摆线齿锥齿轮和准渐开线齿锥齿轮。其中圆弧齿锥齿轮在世界上应用最广泛。弧齿锥齿轮在设计上具有更大的重合度，在传动平稳性、可靠性及承载能力等方面比传统直齿锥齿轮具有更大的优势。

弧齿锥齿轮在一定程度上已经取代直齿锥齿轮，广泛应用在汽车轮船、矿山机械、精密仪器仪表等领域，现阶段弧齿锥齿轮正向高速、重载、高精度方向发展，相信在机械领域中会拥有更加广阔的应用前景。弧齿锥齿轮最早由美国格里森公司提出，以齿轮啮合理论为基础[1～3]，经过多年发展已经形成一套完整的格里森齿轮设计理论与方法。目前，主流的设计方法依然采用格里森公司的设计理论，但由于弧齿锥齿轮的齿廓曲线是标准的球面渐开线，无法展成平面，以齿轮啮合原理为基础的设计方法存在原理性误差，需要不断校正修改才能达到设计精度，由此使弧齿锥齿轮设计工作变得非常繁琐且效率低下。对此，本文基于球面渐开线的形成原理，对弧齿锥齿轮的三维建模提出新的思路与设计方法。

1 球面渐开线的形成

基圆锥OAB 与大圆平面Q 相切且基圆锥的顶点与大圆平面的圆心重合，基圆锥母线与大圆平面Q 的半径R 等长，基圆锥在保持上述条件下与大圆平面作无相对滑动的纯滚动运动（见图1）。由此可知，基圆锥底圆上一点P 与圆锥顶点O 的距离始终保持为大圆半径长R，基圆锥与圆平面Q在作纯滚动运动时，P 点在此过程中的运动轨迹PP′是以点O 为球心以OP 长为半径的球面曲线，通常称为球面渐开线[4]，动点P 运动的轨迹方程可表示为：

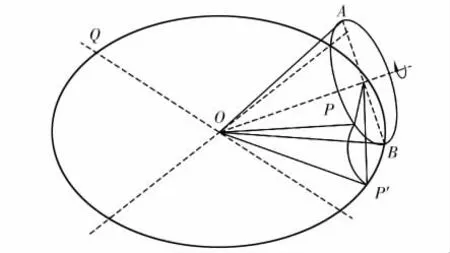
图1 球面渐开线的形成

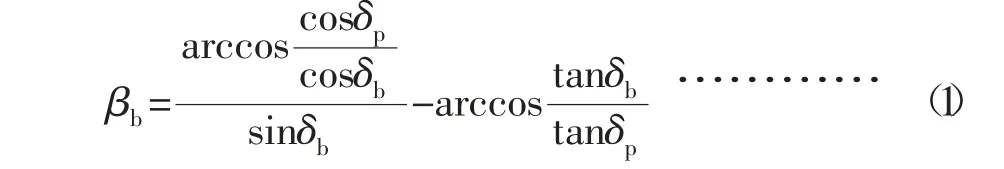
式中：δb—基圆锥角（rad）；δp—球面渐开线上P点所对应的锥角（rad）。

2 球面渐开线数学模型的求解

将基圆锥倒放并以之为参考建立三维直角坐标系，圆锥顶点作为坐标系原点O，将OO′作为Z 轴（O′为基圆锥底圆圆心），大圆平面与基圆锥侧面相切并沿之作纯滚动（见图2）。在初始时，大圆平面与坐标系XOY 面垂直（即点Mp与Mo重合时），两平面的交线即发生面与基圆锥的切线OMp。大圆平面上Mo点轨迹展开为球面渐开线MoMp，点M、Mp在XOY 平面的投影点为M1、Mp1，连接OM1和OMp1，根据渐开线性质可知弧长MMo=MMp。过点Mp作OM 的垂线，垂足为N，三角形ONMp为直角三角形，过点Mp1作OM1的垂线，垂足为N1，连接NN1。

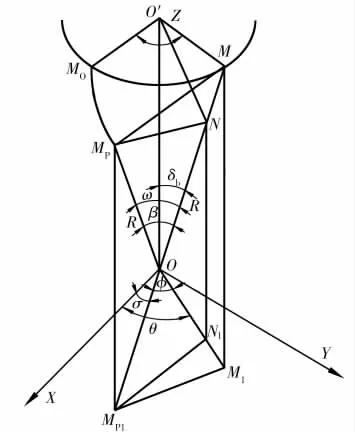
图2 球面渐开线数学模型

经推导，Mp点的空间坐标方程为[2]：

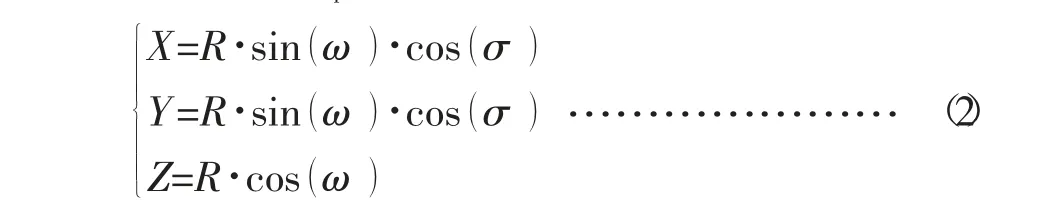
式中：R—基圆锥锥距（mm）；ω—矢径OMp与Z轴之间的夹角（rad）；σ—矢径OMp在XOY平面内的投影OMp1与X 轴的夹角（rad）。

3 齿轮端面齿廓与齿形线的形成

根据弧齿锥齿轮的设计理论，弧齿锥齿轮设计的首要工作是确定以下设计参数并构建相应关系表达式：

3.1 大小端双侧齿廓的建立

根据弧齿锥齿轮锥基本设计理论可以得到其分度圆齿厚角为：

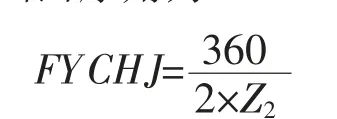
以从弧齿锥齿轮副的动轮为研究对象（故齿数为Z2）。由式（1） 球面渐开线轨迹方程可得分度圆处的偏角beta、齿顶圆处的偏角beta_a 及齿根圆处的偏角beta_f 分别为：

分度圆处偏角

可求得基圆齿厚角JYCHJ、顶圆齿厚角DYCHJ 和根圆齿厚角GYCHJ：

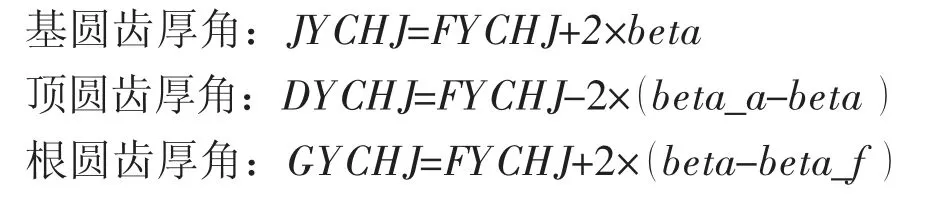
（1） 大端双侧齿廓曲线方程

前文中已经将齿廓曲线上任一点的球坐标参数关系式表示出来，现将球坐标系转化为直角坐标系方程，其中大端一侧齿廓曲线方程为：

3.2 大小端面齿根与齿顶圆弧方程

（1） 大端齿顶圆弧

大端齿顶圆弧可以看作从齿顶圆中截取某一段圆弧，具体过程为保持矢径在球坐标系中与Z 轴的夹角不变（夹角为顶锥角），然后矢径从某一点开始绕着Z 轴旋转一定角度后矢径端点所划过的圆弧，方程可表示为：

小端齿顶、齿根圆弧的创建与大端大致相同，

在建立小端两侧齿廓与齿顶、齿根圆弧曲线方程时，与大端有所不同：

①小端矢径为内锥距R1。

②小端矢径与X 轴初始夹角为齿轮小端与大端之间的偏角Q12。

3.3 齿形曲线的形成

齿形曲线的绘制是设计弧齿锥齿轮的关键。首先需要确定刀盘中心位置，根据刀盘中心位置能够确定齿形线终点相对于起始点的偏角大小，确定好偏角大小就能够建立齿形线方程。由文献[6～7]可推导出：

4 基于UG/Open GRIP 的建模模块

图3 单齿轮廓曲线

UG/Open GRIP 是用于UG 二次开发的软件工具，UG/Open GRIP 语言创建类似FORTRAN 的程序，与Unigraphics 系统集成，运用GRIP 程序能够完成各种交互操作。例如，完成实体建模、工程制图、加工制造等任务。GRIP 语言有自己的语法结构、程序结构、内部函数，同时它也是其他通用语言程序相互调用的接口。通过运用GRIP 语句构造相应的点、线、面从而将齿形齿廓曲线的生成、齿面的创建及单齿和全齿实体模型生成过程统一起来，实现弧齿锥齿轮的全参数化建模功能。利用GRIP 人机交互界面改变齿轮的相应设计参数就能够获得所需的弧齿锥齿轮[8]，由此简化弧齿锥齿轮三维模型的设计过程。

4.1 创建UG 可执行程序文件

GRIP 程序文件编写完成之后需要经过编译链接才能够被UG 运行。

首先创建文本文档（.txt） 并将其保存为.grs 格式文件，然后根据弧齿锥齿轮球面渐开线数学模型特点编写程序；打开UG/OPEN GRIP 界面（见图4），将编写完成的.grs 文件编译生成.gri 目标文件；点击LINK 对目标文件进行连接生成.grx 文件。此时程序便可被UG 执行。

图4 程序文件编译器

4.2 程序的调用与界面的生成

运行UG，在UG 菜单种点击“文件”-“执行”-Grip，生成弧齿锥齿轮参数化建模界面（见图5）。

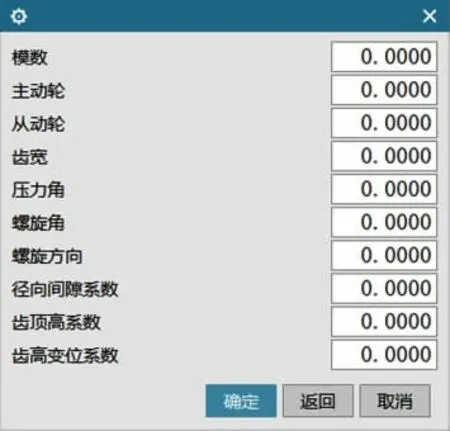
图5 弧齿锥齿轮参数化建模界面

4.3 创建齿轮实体模型

在参数化建模界面分别输入主动轮与从动轮的设计参数，创建出齿轮实体模型（见图6～图7）。

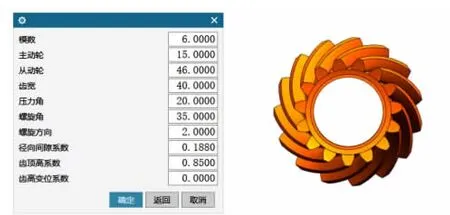
图6 主动轮

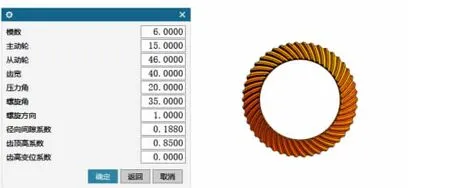
图7 从动轮

5 结 语

本文以球面渐开线形成原理为基础，创建弧齿锥齿轮齿形齿廓曲线方程，利用UG 二次开发工具UG/OPERN GRIP 创建参数化建模模块。通过修改齿数、压力角、螺旋角、模数等参数可以生成新的球面渐开线弧齿锥齿轮三维模型，实现弧齿锥齿轮建模任务的尺寸驱动功能，提高弧齿锥齿轮的建模效率，为其他复杂模型的设计工作提供参考。