一种3(Ra)PS变胞并联机构构型与运动学分析

2022-03-14李端玲雷志强张元开

农业机械学报 2022年2期

贾璞李端玲雷志强张元开杨超

(1.北京邮电大学自动化学院，北京 100876； 2.陕西科技大学机电工程学院，西安 710021)

0 引言

传统的并联机构具有恒定的拓扑结构和固定的自由度[1]，这限制它们的多功能性和适应性。随着工业快速定制和环境变化的要求，可以适应不同场景的可重构并联机构成为近年来机构研究的热点。近年来学者们进行许多可重构并联机构(RPM)的研究。在此基础上，也产生了一类具有自适应性和可重构特性的变胞并联机构(MPMS)[2]。DAI等[3]提出用于装饰性纸箱折叠和可重构包装研究的变胞机构。YAN等[4-5]研究运动关节的可变构型，给出变胞关节的构型表示。KONG[6-7]使用基于螺旋理论构造出具有多种操作模式的RPM。现有可实现RPM具有可重构特性的方法主要包括引入变几何约束或可锁定的铰链[8-10]，以及在运动支链中集成一些可重构连杆机构[11]。LI等[12]使用基于位移子群的方法提出一类带有Schoenflies运动分支的RPM。GAN等[13-15]发明变胞rT铰链和rR铰链，并提出使用这些铰链构造RPM的方法。ZHANG等[16]提出vA(可变轴线)铰链，其灵感来自于折纸，并已将其集成到多个RPM中。CARBONARI等[17]通过引入特殊的可锁定万向节设计一类RPM。这些变胞或可锁定铰链的构态变化会导致RPM的自由度发生变化。文献[18-19]通过整合运动支链中的可重构连杆，提出几种RPM，并对含有vA铰的并联机构建立涵盖所有构型的运动学模型。胡旭宇等[20-21]提出一系列含恰约束支链的并联机构和球面变胞仿生机构。畅博彦等[22]研究了一种变胞机构运动参数输入与输出之间的映射关系。沈惠平等[23]通过拓扑降耦设计一种实现一平移两转动的并联机构，并推导出其符号正反解。温如凤等[24]提出具有耦合分支的两转两移型并联机构，并对其刚度、工作空间等性能进行对比分析。

本文研究一种由新型变胞铰链Ra铰组建而成的3(Ra)PS变胞并联机构。重点分析3(Ra)PS并联机构的构型，针对不同构型使用螺旋理论验证构型的自由度变化特点。根据Sylvester结式消去法，利用Mathematica符号工具对3(Ra)PS变胞并联机构的所有构型进行正、逆运动学分析求解和数值验证。以期为变胞并联机构的设计提供思路，为多构型并联机构的运动学建模提供新的方法。

1 可重构(Ra)PS支链

可重构(Ra)PS支链由Ra铰链、P副(移动副)和S副(球副)组成。该支链的可重构特性来源于Ra铰链的结构变化。如图1所示，Ra铰具有3个旋转自由度(DOFs)，这3个自由度分别来自于3个垂直交叉的旋转轴(外轴、内轴和垂直轴)。Ra铰的外轴为一个方向固定的轴，内轴可在开槽环内旋转，改变自身在开环槽中的位置。此外，垂直轴用于为内轴位置的位置变化提供旋转。开槽环用于固定内轴线两端的滑块，并通过滑块沿开槽环的内槽自由旋转和固定，使其具有改变内轴位置方向的能力。

图1 Ra铰三维模型Fig.1 Structural diagram of Ra joint1.定位孔 2.保持架 3.开槽环 4.滑块

如图2所示，内轴位置的变化可使Ra铰链的自由度发生改变，从而导致(Ra)PS支链具有2个不同的构态。在图2a中，内轴与外轴垂直，此时支链等效为SPS支链，为(Ra-1)PS支链，在图2b中，内轴与外轴共线，支链等效为UPS支链，为(Ra-2)PS支链。

图2 (Ra)PS支链的两种构型Fig.2 Two configurations of (Ra)PS limb

如图2a所示，在Ra铰链中心处设置一个支链坐标系o1x1y1z1，x1轴与外轴共线，y1轴位于保持架平面内并垂直于外轴，z1轴的建立符合右手准则。(Ra-1)PS支链的运动螺旋系统为

(1)

式中β——支链($13)与平面y1o1z1之间的夹角

α——支链$13与平面x1o1y1的夹角

l——Ra铰链中心和球铰中心之间的距离

符号cα和sα分别表示cosα和sinα。当Ra铰处于(Ra-1)构型时，β、γ(γ为内轴线与外轴线的夹角)都不为零，当Ra铰处于(Ra-2)构型时，β和γ为零但α不为零，在旋量符号$ij中，下标i表示支链编号，下标j表示支链内的运动副编号。式(1)中的7个螺旋形成一个六阶系统，这表明(Ra-1)PS支链具有6个自由度(DOFs)，并且对与其连接的动平台不提供任何约束。

对如图2b所示的(Ra-2)PS支链建立的运动旋量系统为

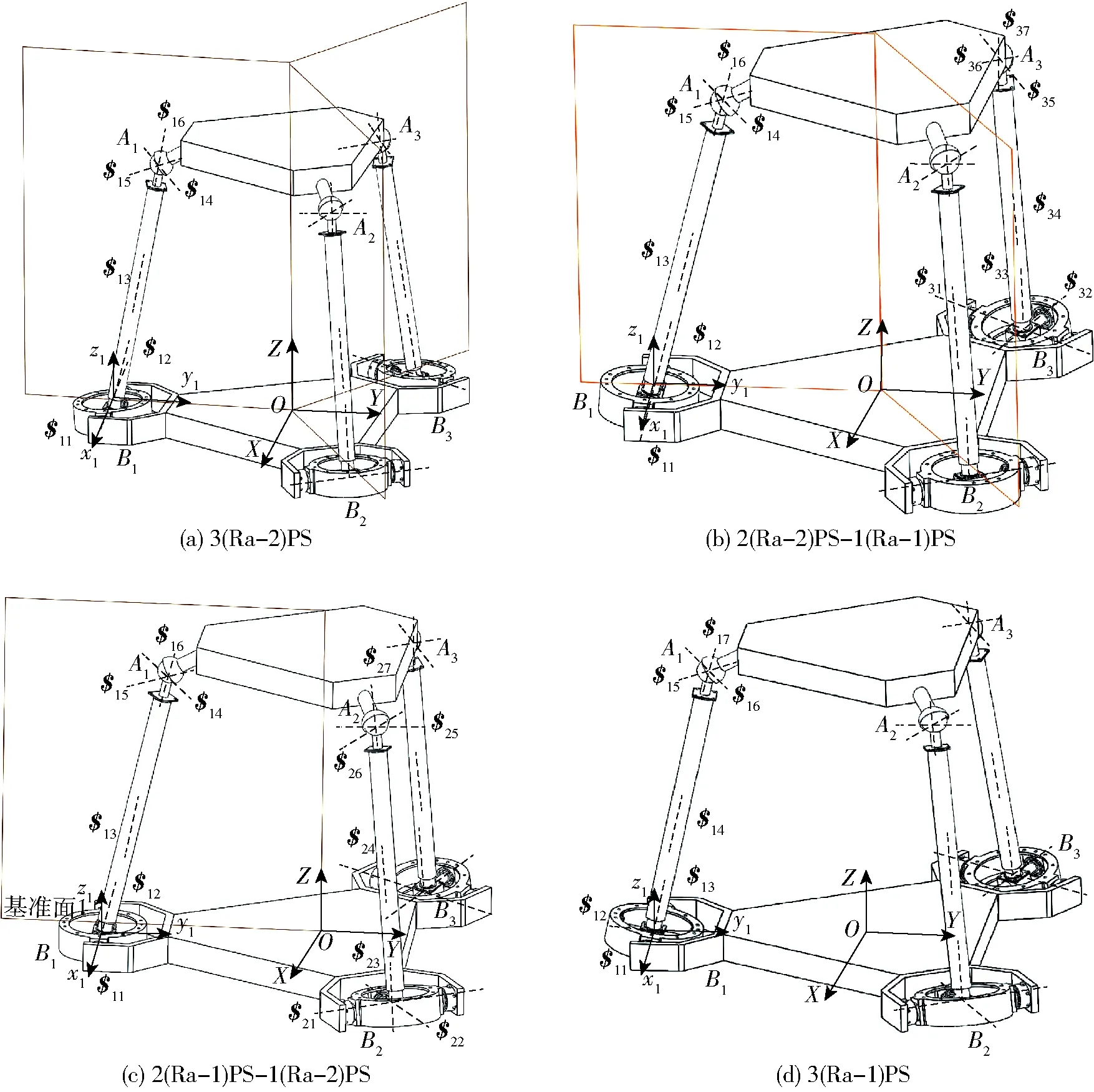
图3 3(Ra)PS变胞并联机构的4种构型Fig.3 Four configurations of 3(Ra)PS metamorphic parallel mechanism

(2)

从式(2)可以看出，旋量$12和$16相同，并且6个旋量形成一个五阶螺旋系统。因此，对支链的运动螺旋系统中求反螺旋可以得到(Ra-2)PS支链的约束螺旋为

(3)

从式(3)可知，这个支链提供一个作用于球铰中心且平行于支链Ra铰外轴线的约束力，导致球铰中心A1被约束在垂直于外轴线的平面y1o1z1内，除此之外支链位于该平面内。因此球铰中心A1只能在平面上移动。因此，(Ra-2)PS支链有5个自由度，比(Ra-1)PS构型少1个自由度。

2 3(Ra)PS并联机构构型分析

如图3所示，将3个(Ra)PS支链分别与动平台和底座连接，三支链对称布置，此时可以获得4种不同构型的并联机构。

其中点Ai为球形铰链的中心点，点Bi为支链i的Ra铰链中心，在等边三角形B1B2B3的几何中心O处建立定位坐标系OXYZ，其中X轴平行于B2B3，Y轴穿过B1并垂直于B2B3，Z轴垂直于底座。如图3a所示，将3个(Ra-2)PS支链与底座和动平台连接可组成3(Ra-2)PS变胞并联机构，根据式(2)中的几何约束可知，当支链为(Ra-2)PS时，球铰中心Ai被约束在平面Σ0上。

根据上述描述，点Ai和Bi在全局坐标系中的位置矢量可表示为

(4)

式中支链i和矢量OBi之间的夹角为αi，定坐标系中的点Ai和Bi的位置矢量分别为ai、bi，球铰链中心Ai与Ra铰链中心之间的距离为li。rb为底座外接圆半径。

从式(4)可以看出，每一个(Ra-2)PS的支链对动平台提供一个过球副中心且平行于Ra铰外轴方向的约束力。因此，图3a中3(Ra-2)PS并联机构在全局坐标系下的约束螺旋系统可表示为

(5)

对式(5)求反螺旋，动平台的运动螺旋可表示为

(6)

由式(6)可知，支链对称分布的3(Ra-2)PS并联机构具有分别沿X、Y轴的2个旋转自由度和沿着Z轴的1个移动自由度。

将3(Ra-2)PS并联机构中的支链从(Ra-2)PS改为(Ra-1)PS后，将产生具有更多自由度的构型。将支链1的构态从Ra-2改变为Ra-1后，3(Ra-2)PS变为如图3b所示的2(Ra-2)PS-1(Ra-1)PS构型，其中在支链2和3分别具有一个平行于各自Ra铰外轴线的约束力。基于约束螺旋分析，2(Ra-2)PS-1(Ra-1)PS并联机构具有4个自由度，1个平移和3个旋转(3R1T)。

进一步改变支链的构态，如图3c所示的构型为2(Ra-1)PS-1(Ra-2)PS构型，此时只有支链3具有1个力约束，其余两个支链对平台没有约束。因此，该机构具有5个自由度，其中包括3个旋转和2个平移的自由度(3R2T)。

当将第3支链的构态都改变为(Ra-1)PS时，此时机构的构型为3(Ra-1)PS，如图3d所示，该构型3(Ra-1)PS对平台没有任何约束螺旋且并联机构具有6个自由度。

3 变胞并联机构的驱动方案

由第2节对变胞并联机构3(Ra)PS的构型分析可知，为使机构具有稳定可控的能力，合理的驱动选择必不可少。因此机构的驱动选择不仅要尽可能保持与底座的连接，还要考虑机构的运动是完全可控的。如果机构选择合理的驱动方案，在锁定所有驱动运动铰链后，并联机构的约束螺旋系统的阶数应为6，运动动平台将失去所有6个自由度。

为实现机构不同工作模式之间的灵活性和正常切换，保证机构的优良动态性能，在与底座直接连接的每个支链中的外轴、内轴、移动副可以作为驱动选择。

由于(Ra)PS支链两种构态的约束不同，因此对应的驱动选择也不完全相同。在(Ra-2)PS支链中，围绕外轴线的旋转或沿着移动副的平移可以用作驱动。根据图2b和对应的支链运动螺旋，分别锁定这两个输入可以形成驱动约束螺旋为

(7)

当改变(Ra-2)PS支链到(Ra-1)PS时，Ra铰的内轴转动副可以作为一个新的驱动选择。锁定该驱动产生的驱动约束力为

(8)

通过上述分析可知，满足驱动方案的原则是，驱动约束螺旋与动平台约束螺旋系统形成一个六阶约束系统。在此基础上，对3(Ra)PS变胞并联机构的驱动方案总结如下：①当3(Ra)PS并联机构含有支链(Ra-2)PS时，外轴转动副和移动副可以作为驱动选择。②当3(Ra)PS并联机构含有支链(Ra-1)PS时，外轴转动副、移动副和内轴转动副中的任意两个可以作为驱动选择。

将图3b中的2(Ra-2)PS-1(Ra-1)PS并联机构作为示例。根据第2节分析可知在该构型下机构具有4个自由度，其中每个(Ra-1)PS支链有3个选择，其中任意2个可以作为驱动，每个(Ra-2)PS支链有2个选择，其中任意一个可以作为驱动。现将(Ra-1)PS支链的移动副和内轴转动副和(Ra-2)PS支链的移动副作为驱动方案，2(Ra-2)PS-1(Ra-1)PS并联机构的驱动约束螺旋系统为

(9)

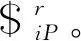
对上述驱动选择方案展开分析，拓展到变胞并联机构的所有构型，对应构型的驱动选择数目如表1所示。

表1 所有构型驱动选择数目Tab.1 Drive options for all configurations

4 运动学建模与位移分析

4.1 运动学建模

考虑到(Ra)PS支链的两个构态之间的差异，可以发现，引起两种构态变化的关键原因是内轴的旋转导致内外轴线共线，当内外轴线共线时，Ra铰等效为一个虎克铰，当内外轴线不共线时，Ra铰等效为一个球铰。

根据第3节中的驱动分析方案，将(Ra-1)PS支链的内轴的转动、外轴的转动和移动副作为驱动输入。因此，(Ra-2)PS可视为(Ra-1)PS支链的一种特殊构态，通过在βi=0时锁定内轴驱动。支链的这种特性为3(Ra)PS变胞并联机构的统一几何和运动学建模提供可能，它可以覆盖3(Ra)PS变胞并联机构的所有构型。因此，在(Ra-2)PS支链中将移动副作为驱动选择，在(Ra-1)PS支链中，将内轴的旋转和移动副作为驱动选择。

在全局坐标系下，3(Ra)PS变胞并联机构的所有构型的约束关系可以表示为

(10)

当支链为(Ra-1)PS时，β≠0；支链为(Ra-2)PS时，β=0。其中，li是支链长度，R(k,g)表示绕k轴旋转一定角度g。

在此基础上，将3(Ra)PS的几何约束分为两部分进行描述。第一部分支链长度的约束方程为

(11)

第二部分每个支链的移动副的方向与Ra铰的内轴轴线方向始终垂直，即

(Ra′i+P-bi)Tsi=0 (i=1,2,3)

(12)

式中动平台坐标系相对于全局坐标系的旋转矩阵为R，动平台原点在全局坐标系中的位置矢量为P=(px，py，pz)，球铰中心Ai在动平台坐标系下的位置矢量为a′i，Ra铰内轴轴线的单位方向向量为si。

4.2 逆运动学分析

根据给定动平台的原点位置P和姿态R获得驱动参数(支链长度li、内轴旋转角βi)来分析3(Ra)PS变胞并联机构的逆运动学。如图4所示，将动平台坐标系Puvw的原点建立在动平台原点上，其中v穿过A3并垂直于A1A2，w轴垂直于动平台，u轴的建立符合右手准则。

图4 动平台的局部坐标系Fig.4 Local coordinate system of moving platform

当给出在全局坐标系下动平台的位置P和姿态矩阵R后，球形铰链的中心Ai的位置可以表示为

(13)

其中

式中ra——动平台外接圆半径

在4种自由度的构型中，包含(Ra-2)PS支链的构型在求反解时平台的位置和姿态参数不能随意给定。它们应遵循方程(12)中的几何约束关系，基本规则是：当支链i处于(Ra-2)PS构型时，球铰原点Ai被约束在平面Σ0内，因此Ai的位置矢量应与平面Σ0的法向量垂直，可得关系式

aini=0 (i=1,2,3)

(14)

其中

将式(13)代入式(14)可以获得关系式为

(15)

将式(13)代入式(11)，可以对3(Ra)PS机构的逆运动学进行求解，即

(16)

由第2节分析可知，当支链为(Ra-2)PS时，β1=β2=β3=0。然而当支链为(Ra-1)PS时有

(17)

4.3 正运动学分析

与逆运动学分析相反，正运动学分析是在给出每个构型对应的驱动参数(li,βi)的前提下，求解平台位置P和姿态矩阵R。3(Ra)PS变胞并联机构的正运动学分析方法是利用支链参数表示球铰中心矢量ai，建立基于平台几何参数的约束方程。根据图4，动平台几何约束可以描述为

(18)

(19)

其中fi(·)是关于ti的线性函数，方程系数仅取决于已知的结构参数。对方程组(19)中的前2个方程，使用Sylvester结式消元法消去t1，可以得到一个只含有t2、t3的新方程

(20)

对式(19)中的f3和式(20)中的f4使用相同的方法，可以获得一个只含有未知变量t3的多项式为

(21)

其中系数hi是一个只与输入参数有关的常数。表明方程(21)是一个只包含变量t3的16阶的单变量方程。对式(21)进行求解就可得到16个t3的解。通过将t3的每一个解代入方程(19)中的第3个方程并选择满足的根来求解t2。t1可以通过将t2和t3的每一对解代入方程(19)中的第1个方程求得，并代入式(19)中的第2个方程来验证是否正确。在此基础上，将t1、t2、t3的16对解代入几何约束方程αi=2arctanti中，可以得到每个支链与底座平面的夹角。并通过方程(20)计算出球铰中心Ai的坐标。

如图4所示，动平台的位置和位姿可以使用3个球铰的中心坐标确定，即

(22)

将正解得到的3个Ai的坐标代入式(22)获得动平台坐标系中坐标轴的向量，获得动平台的位置坐标和姿态矩阵。