考虑力学约束的核石墨表面变形场测量研究

王璐，易亚楠，刘广彦，马沁巍，马少鹏

（1. 北京理工大学 宇航学院，北京 100081；2. 上海交通大学 船舶海洋与建筑工程学院，上海 200240）

高温气冷堆是第4 代先进核电技术的代表，具有安全性和发电效率高等优点[1]. 核石墨作为慢化剂、结构材料和反射层广泛应用于高温气冷堆的各种基础建设中[2−3]，因此对核石墨力学性能的研究具有重要意义. 对于材料构件受载变形的测量分析，目前普遍采用应变片等接触式方法进行测量，然后基于测量的离散点信息再进行统计分析. 过少的测量点往往会产生较大的测量噪声，而且应变片实施起来工序繁琐，不利于工程大批量测试要求[4]. 为了更好地对核石墨材料变形状态进行分析，研究非接触、高性能、便捷的测量方法至关重要.

数字图像相关（digital image correlation, DIC）[5]方法又称为数字散斑相关方法(digital speckle correlation method，DSCM)，是一种基于图像分析的非接触变形场测量方法. DIC 利用数字相机记录试件表面的散斑图像，然后对散斑图像进行相关分析获得试件表面的变形场. DIC 方法以其对测试环境要求低、实施简单、测量范围易调节等优势[6]而被广泛接受并应用. 刘刘等[7]基于数字图像相关技术实现了多孔气凝胶基复合材料弹性力学常数的识别. 曾祥福等[8]基于三维数字图像相关技术对铝板及石墨圆柱试件动载下的材料力学行为进行了研究. DIC 方法对于简单表面的简单变形（如伸缩变形）的测量精度基本满足工程测量的需求. 然而，在很多实际工况下，局部变形场（应变高度集中区，如剪切带[9]、试件缺口附近[10−11]和裂纹尖端[12]）的位移测量误差可达到百分之几十像素甚至整像素[13]. 这导致使用者很难判断测量结果的可靠性. 核反应堆中的构件往往结构复杂，存在大量沟槽结构，局部具有应力集中效应，因此常规子区DIC 方法难以满足测量要求. 大多复杂形状试件或结构的力学性能以及破坏过程与其边界的应变状态有重要的关联. 如圆环受压结构，它的破坏往往是从圆环边界开始的[14]. 因此复杂形状试件或结构边界的变形成为很多实验的观测重点. 在多数实际工况下，局部变形场无法通过应变片测量，因为应变片尺寸内高梯度的应变会被平均. 此时，采用DIC 方法虽然能够测量这些高应变梯度区的局部变形场，但由于子区DIC 仅能计算获得子区中心点的变形信息[15]，因此无法直接计算获得边界处的变形信息. 网格DIC[16−17]可以实现包含边界的全场测量，但由于其计算过程复杂、运行效率低下，难以满足工程上大规模测试的要求.

为了准确地获得核石墨构件表面变形场，本文发展了一种考虑力学约束的DIC 方法（mechanicsconstrained，DIC），以下简称为MC-DIC 方法. MC-DIC方法保留了子区DIC 计算便捷的优势，针对其无法实现边界测量、测量结果不具有空间连续性等问题进行了改进. 文章通过模拟实验验证了算法的有效性，并将其成功地应用于真实核石墨圆环对径压缩试件全场变形测量.

1 MC-DIC 基本原理

MC-DIC 的计算流程主要分为两部分：子区DIC计算与考虑力学约束的位移场空间重构. 首先采用子区DIC 进行相关计算获得试件表面位移场和相关系数场；其次通过相关系数[18]确定高精度位移点（以下简称信赖点）；之后采用8 节点等参单元在试件表面构建网格，单元与单元之间通过节点连接形成力学约束；然后基于信赖点实现全部单元节点位移的反演；最后基于得到的单元节点位移实现整个变形场的重构，从而实现试件表面变形场的求解. 流程图如图1 所示.

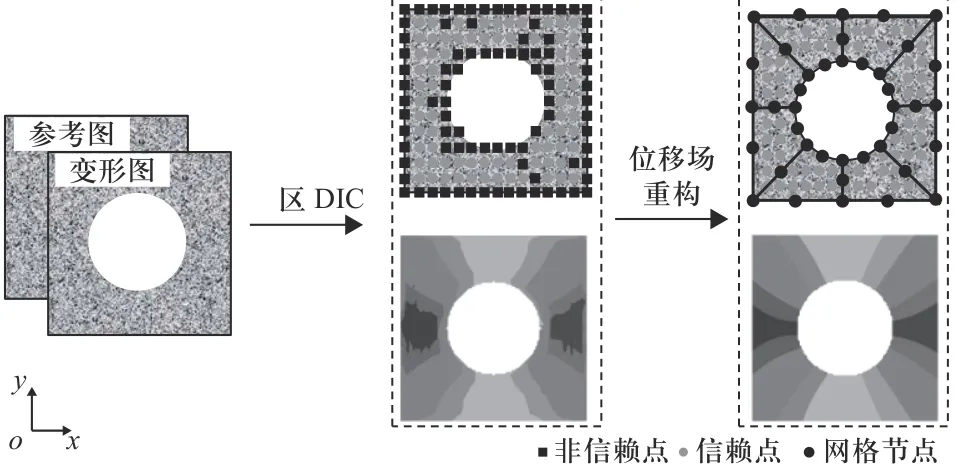
图1 MC-DIC 计算流程图Fig. 1 Flow chart of MC-DIC

相关系数计算如下所示

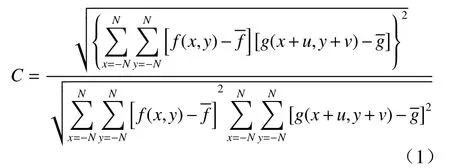
式中：f(x,y) 与g(x+u,y+v)分别为变形前后各像素点的灰度值；与为变形前后计算子区内的灰度平均值；u，v为子区中心点的位移；2N为参考图像子区的宽度.

图1 中黑色方形代表非信赖点，即相关系数较低的像素点；灰色圆形代表信赖点，即相关系数较高的像素点；黑色圆点代表网格节点. 在传统子区DIC计算过程中，由于各种因素的影响，许多散斑点往往无法实现很好地匹配，尤其是试件边界附近，使得这些计算点的相关系数较低. 考虑到试件表面的变形场必然服从力学约束，因此通过信赖点再加上力学先验约束即可求解出高质量的全场变形. 相关系数（式（1））表征了该点位移计算的置信度，相关系数越大（越接近1），表明该位移值计算得越准确. 为了获得高精度的表面变形场，本文选取相关系数C>0.95的计算点作为信赖点. 考虑到已有大量关于子区DIC 原理介绍的文献，此处仅重点介绍位移场空间重构的基本原理.

MC-DIC 空间位移场重构借鉴了有限单元法的思想，将试件表面划分为若干个单元，单元与单元之间通过节点连接，保证了计算区域位移的连续性，符合试件表面真实位移的空间分布[19]. 由于节点位于单元的边界，因此将单元节点布置于试件边界处时即可计算试件边界处的变形. MC-DIC 以每个单元节点的位移作为参数空间，将单元内的信赖点通过形函数与各自单元的8 个节点建立位移约束关系，基于已知信赖点位移通过优化的方式反演出所有节点的位移，之后再基于节点位移重构出单元中所有像素点的位移，如图2. 考虑到实际构件中单元形状的不规则性，此处采用了有限单元法中等参元的思想，将每个单元从全局坐标系xoy中映射到局部坐标系ξoη中，2 个坐标系的数学关系如下

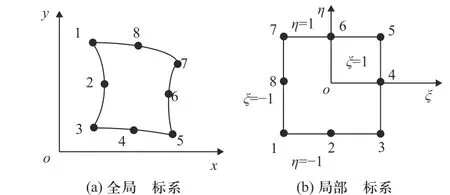
图2 8 节点等参单元中全局坐标系和局部坐标系的关系Fig. 2 Relationship of global and local coordinates in the 8-node quadrilateral elements

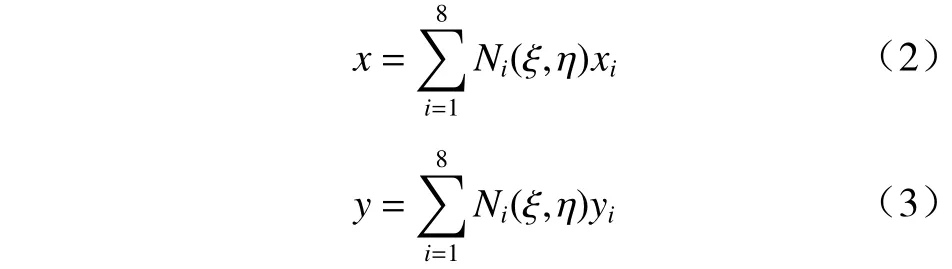
式中：ξ和η为局部坐标系的横纵坐标轴；x和y为全局坐标系坐标轴，Ni(ξ,η)为单元内第i个节点的形函数，与有限元法的形函数相同.

在全局坐标系xoy中，像素点(x,y)的位移可以用局部坐标系ξoη中相对应的点(ξ,η)来表示，即

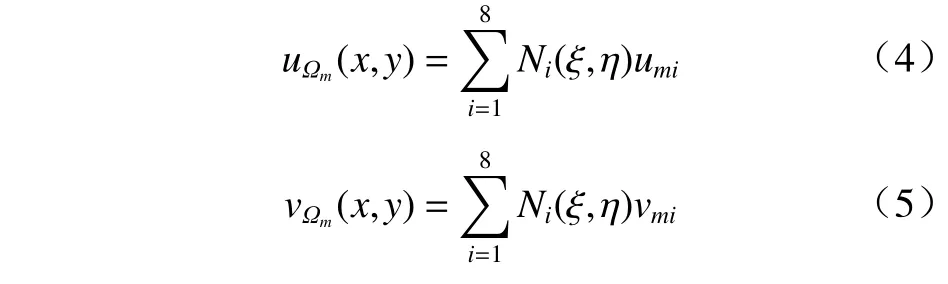
式中：u和v分别为节点沿横轴和纵轴方向的位移；Ω为计算区域；m为单元编号；i为单元内节点编号.

目标函数可表达为

式中：t和h分别为子区DIC 计算得到的信赖点和与之对应的重构位移点；M为目标区域信赖点的数量.因此，位移场的求解最终可以转化为求解Jloss全局最小值问题，此处可以采用NR 算法[20]、LM 算法[21]和遗传算法[22]等，完成求解后可一次性获得全场变形.

2 模拟实验

为验证上述MC-DIC 方法的有效性，首先进行了开孔方板压缩模拟实验，模型示意图及网格划分如图3 所示，线载荷密度为1.4×107N /pixel，杨氏模量E=1010Pa，泊松比v=0.33. 实验以式（6）作为目标函数，采用LM算法进行优化计算，当Jloss的改变量小于10−6或待优化参数变化量小于10−3时候迭代终止.实验所用的参考图像来源于真实的散斑图像，图像采用8 bit 编码，灰度介于0～255 之间. 变形图像通过参考图像使用立方插值生成，每个整像素点的位移由开孔压缩理论解（式（7）～（9））生成

图3 开孔方板模型示意图及MC-DIC 网格布置图Fig. 3 The geometry of open-hole specimen and meshing scheme in MC-DIC

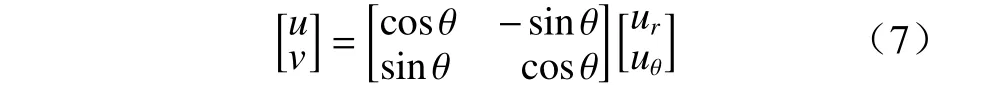
式中：

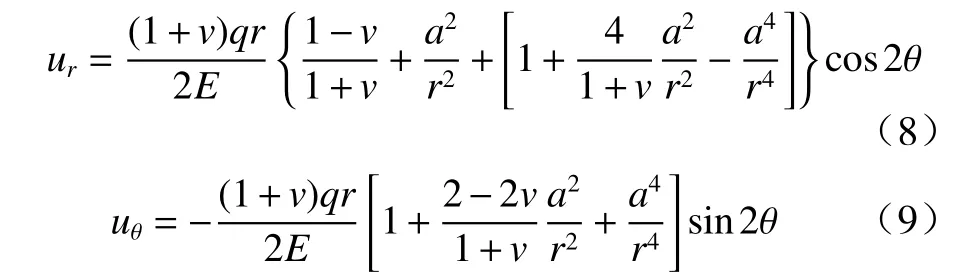
分别采用子区DIC 和MC-DIC 求解位移场，子区DIC 的相关窗设置为9 pixels，计算结果图4 所示.图4（a）为采用式（7）～（9）生成的理论解；图4（b）为采用子区DIC 方法计算得到的位移场；图4（c）为MC-DIC 计算得到的位移场，其选用相关系数0.95 的点作为信赖点. 图4（d）为MC-DIC 计算得到的位移场，但其选用相关系数C>0 的点作为信赖点，即所有DIC 计算点都参与空间重构. 从图中可以看出，图4（b）所示位移场不光滑且不具有连续性，尤其是在模型边界处变形更为明显. 图4（c）与图4（a）最为接近，位移场光滑并具有连续性. 图4（d）计算得到的位移场也光滑并具有连续性，但由于采用所有计算点进行重构，大量低匹配度的位移点严重影响了重构效果.为了更加直观地展示出不同方法的计算效果，图5 给出了图3 黑线处计算得到的像素点位移（从左至右）. 从图中可以看出DIC、MC-DIC(C>0.95)与理论解在非边界区域计算结果较为吻合，考虑信赖点的MC-DIC(C>0.95)在边界区域的计算结果与理论解更为接近. 这表明MC-DIC 方法在考虑信赖点的情况下可以很好地实现材料全场变形测量.

图4 不同方法计算得到的位移场Fig. 4 Displacement fields obtained by different methods

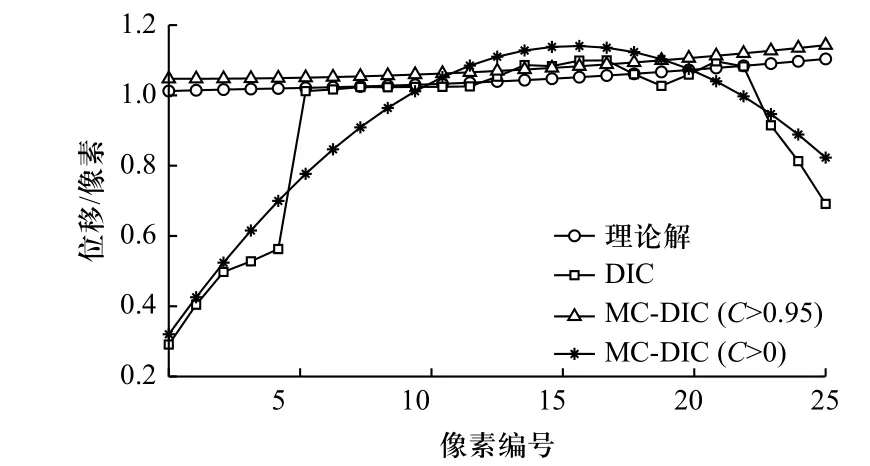
图5 不同方法计算得到的图3 黑线处位移Fig. 5 Displacement obtained by different methods (blackline in Fig.3)

3 实 验

为了获得核石墨构件表面高精度变形场，本节采用MC-DIC 方法对其表面变形场进行测量. 图6 与表1 给出了核石墨圆环构件的尺寸和材料参数，实验采用WDW-50E 试验机，利用位移加载方式，加载速度为0.05 mm/min，CCD 相机的分辨率为1 628×1 236. 试验采用50 mm 长焦镜头来捕捉目标区域的散斑图像，采集帧率为1 fps(图7). 试件的表面喷涂不规则的散斑用于追踪像素点的位移量. 获得的图片采用VIC-2D 进行处理，子区大小为47 pixels，计算步长为10.

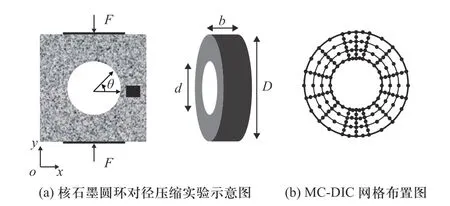
图6 核石墨圆环对径压缩实验示意图及MC-DIC 网格布置图Fig. 6 Diametrical compression test diagram of the nuclear graphite ring and meshing scheme in MC-DIC

图7 核石墨圆环对径压缩试验布置Fig. 7 Experimental setup of nuclear graphite diametrical compression test

表1 核石墨圆环尺寸及材料参数Tab. 1 Ring specimen dimensions and mechanical properties of nuclear graphite

图8 展示了子区DIC 与MC-DIC 计算得到核石墨圆环表面位移场. 从图8 中可以看出MC-DIC 计算结果（图8（c）8（d））更加平滑，其包含了圆环边界的变形信息. 子区DIC 无法获得边界变形信息，由于计算位移点之间并没有力学约束，因此计算得到的位移场并不连续. 由于子区DIC 无法计算出核石墨边界处的变形信息，因此无法通过子区DIC 计算结果准确获得材料的力学参数，例如拉伸破坏应变和抗拉强度等.

图8 不同方法计算得到的核石墨圆环位移场Fig. 8 Displacement fields of nuclear graphite ring calculated by different methods

为了更加直观地感受2 种方法计算的效果，图9给出了图6 黑色标记处的三维形貌图. 从图中可以直观地看出，相比于子区DIC 计算结果凹凸不平，MC-DIC 计算结果更为平滑，更具有连续性.

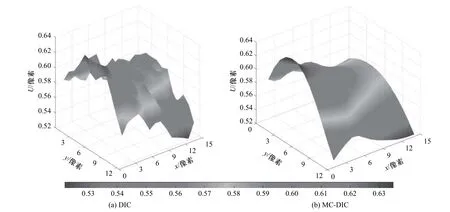
图9 不同方法计算得到的图6 黑色标记处三维形貌图(水平位移场U)Fig. 9 3D Morphology map (horizontal displacement field) obtained by different methods

4 结 论

本文在子区DIC 的基础上发展了一种考虑力学约束的变形测量方法，通过模拟实验对算法的准确性进行了验证，并成功地应用到真实核石墨试件表面变形场的测量中，得到如下主要结论：

①与传统子区DIC 相比，考虑力学约束的MCDIC 计算结果具有空间连续性，符合材料真实变形行为，可以更好地实现材料表面高精度变形场测量.

②基于MC-DIC 方法可以实现材料边界变形测量.

③MC-DIC 方法可以推广到其他材料变形的测量中，为材料的大批量试验及保证测试数据可靠性提供了方便和保障.