弹道修正引信滚转角未知条件下MIMU快速初始对准方法

金磊，胡宝远，申强，王晗瑜，邓子龙

（北京理工大学 机电学院, 北京 100081）

二维弹道修正弹药作为一种介于无控弹与导弹之间的新型精确打击弹药，以其低廉的价格、较高的打击精度而备受青睐，二维弹道修正技术成为了当前弹药领域的热点研究方向之一[1]. 二维弹道修正弹药通常采用“双旋体”结构，弹道修正引信为修正弹前体，与修正弹后体通过轴承连接以保证前体与后体隔离[2]. 修正引信减旋后相对地面滚转姿态保持稳定，以便于舵机执行部件接收制导控制指令产生对弹丸稳定大小和方向的操纵力. 微惯性测量组合(miniature inertial measurement unit，MIMU)在引信内处于微旋或不旋的状态，用来为弹体姿态控制、导引装置稳定跟踪时提供必要信息. 利用MIMU 对弹道参数进行检测时，需要对其进行初始对准. 常用方法是在地面静基座下采用重力矢量和地球自转角速率矢量通过解析方法实现粗对准，然后利用最优估计方法进行精对准[3]. 对于火炮发射的弹丸，由于弹药发射时需要承受高过载等恶劣环境，导致初始对准参数在弹药发射后不再适用. 在弹丸飞行过程中进行初始对准时，常采用地磁传感器测量弹丸的滚转姿态信息[4]，利用外界提供的的位置速度信息或伪距伪距率信息辅助MIMU 实现精对准. 但这种方法需要在弹上额外增加地磁测量元件，在引信组件体积有限时难以适用，而且易受到强磁环境的干扰，当弹体与地磁场方向平行时，会产生奇异点输出. ABBAS[5]、程子健[6]、孙进[7]和KUBO 等[8]分别采用不同方法研究了大方位失准角条件下的初始对准问题，但未考虑到失准角完全未知的情况以及在弹上使用时对准时间长、计算量大等情况.

因此提出了一种适用于火炮发射和修正弹的弹道修正引信滚转角未知条件下MIMU 快速初始对准的算法. 首先基于BP 神经网络算法实现了对弹药前体（一般为修正引信）减旋后滚转姿态的粗略估计，然后建立了大滚转失准角下的非线性对准方程，利用卫星提供的信息辅助惯性导航系统进行精对准，最后通过仿真验证了该方法的可行性与精度. 文中的滚转角均指的是双旋体结构前体修正引信的滚转角.

1 双旋体二维修正弹初始对准全过程及MIMU 组合安装方式

双旋体二维修正弹在发射后首先完成弹道修正引信的减旋，使修正引信停到某未知的固定位置，接着进入粗对准阶段，获取粗略的姿态信息，粗对准结束后利用卫星信息辅助惯性导航系统进行快速精对准，达到所需精度后即可对弹道进行修正，过程如图1 所示.

图1 初始对准全过程示意图Fig. 1 Schematic of initial alignment

图2 为微惯性测量组合在弹上的安装方式，OXnYnZn（ n 系）和OXbYbZb（b 系）分别为导航坐标系和测量坐标系，两个坐标系原点均位于引信质心，测量坐标系三轴方向与弹体坐标系三轴方向一致，选用北天东（NUE）坐标系作为导航坐标系. 图2 中，圆代表单自由度陀螺，矩形代表加速度计，分别安装在测量坐标系的三个轴上. 测量坐标系依次经过偏航 ψ、俯仰 θ和滚转 γ的顺序机动可与导航坐标系重合.

图2 导航坐标系与测量坐标系Fig. 2 Navigation coordinate system and measurement coordinate system

2 基于BP 神经网络的滚转角的粗对准

2.1 速度误差模型

在捷联惯导系统中，由于误差源的存在，实际计算的导航坐标系（ n′）与理想导航坐标系（n 系）之间存在偏差，假设n 系经过3 次欧拉误差角转换后与n′系重合，3 次转动的角 度分 别为 αy、 αz和 αx，记矢量α=[αxαyαz]T，考虑到俯仰角误差和偏航角误差为小量，滚转角误差为任意值，忽略二阶小量，得到滚转角为大失准角的非线性误差模型以及n 系到 n′系的姿态矩阵[5]分别为

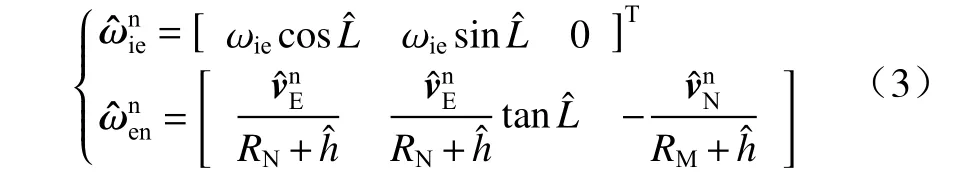
式中： ωie为地球自转角速率大小；、、为惯导解算纬度、经度与高度位置；设 δL和 δh为纬度、高度位置误差，且误差为小量；RM、RN分别为子午面曲率半径和卯酉面曲率半径，由式（3）采用微分法近似可得

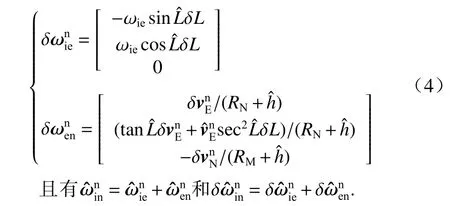
2.2 基于BP 神经网络的滚转角估计

根据Kolmogorov 定理[9]可知，总存在一个3 层的神经网络，在隐含层节点个数足够的情况下，实现对任意非线性函数的无限逼近. 基于神经网络这一特性去逼近速度误差模型，预测滚转角误差.

在装药号（初速）相同条件下，分别从射角35°～50°每隔1°提取一条弹道信息，通过捷联惯导反演算法[10]分别生成滚转角−180°～180°的加速度计和陀螺仪的信息. 第5 s 减旋完成后，MIMU 利用卫星提供信息作为初始导航参数，初始解算滚转角默认为0°，获取10～11 s 内的捷联惯导解算速度，将卫星测量速度与捷联惯导解算的速度相减，从而得到不同弹道不同滚转角对应的速度误差，将速度误差数据、弹道射角和对应滚转角误差(实际滚转角与初始滚转角差值)保存，得到训练样本. 采用图3 所示的BP 神经网络[11]进行训练.

图3 3 层BP 神经网络结构Fig. 3 Three layer BP neural network structure

BP 神经网络通过反向传播对各层神经元权值与阈值进行修正，直至符合精度要求.

图4 为神经网络训练后选取4 条不同弹道的滚转角误差预测结果，其中修正引信减旋后的滚转角随机选取，从图4 中可以看出，采用BP 神经网络预测滚转角误差分布在±20°以内. 图5 为修正引信减旋后的滚转角分别处于−90°、0°、90°和180°时的滚转角误差预测结果，滚转角误差都分布在±20°以内，这表明所建立的BP 神经网络模型能够实现在修正引信减旋后对滚转角的预测.

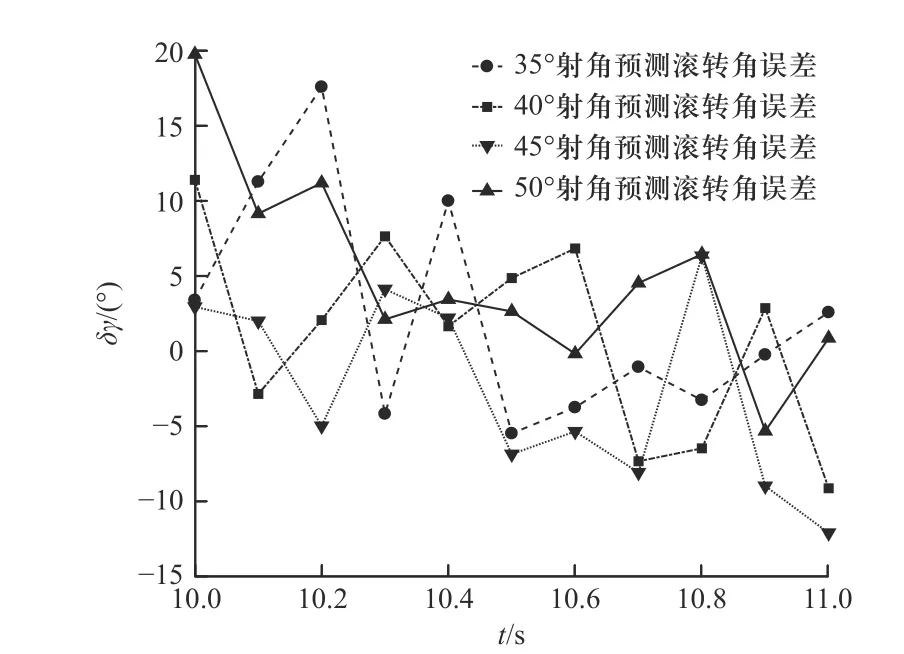
图4 不同弹道滚转角误差预测结果Fig. 4 Error prediction result of roll angle of different trajectory

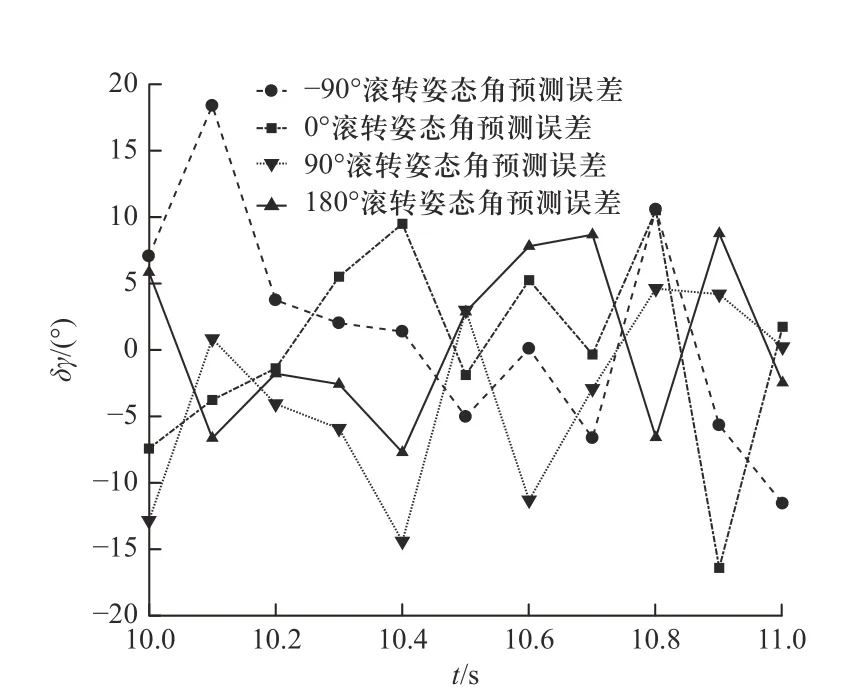
图5 修正引信不同滚转姿态的滚转角误差预测结果Fig. 5 Error prediction result of the roll angle of correction fuse with different roll attitude

为了进一步研究使用训练好的BP 神经网络对不在训练集内的弹道进行滚转角预测的效果，在同一装药号即同一初速条件下分别生成了射角为10°、20°、30°、55°和60°的弹道信息并进行了滚转角的预测，滚转角预测误差如图6 所示. 从图6 中可以看出，利用训练集内的弹道数据生成的BP 神经网络模型能够对训练集外的弹道进行滚转角的预测，随着训练集外弹道射角与训练集内弹道射角范围的偏差增大，其滚转角预测误差也随之增大. 图7 为在训练集外随机选取的某条弹道，当修正引信减旋后的滚转角分别处于−90°、0°、90°和180°时的滚转角误差预测结果，结果进一步验证了使用训练好的BP 神经网络模型能够实现对训练集外的弹道进行滚转角的预测.

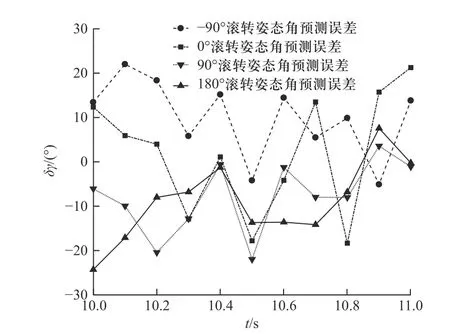
图7 训练集外不同修正引信滚转姿态的滚转角误差预测结果Fig. 7 Error prediction result of the roll angle of correction fuse with different roll attitude outside the training set

3 精对准

由2.1 节得到了速度的非线性误差模型以及实际计算的导航坐标系（ n′） 与理想导航坐标系（ n系）之间的关系，设 n′系 相对于n 系的角速度为 ω，则可得 ω与 欧拉误差角 α之间关系

αy和αz利用小角度原理近似，忽略二阶小量得到

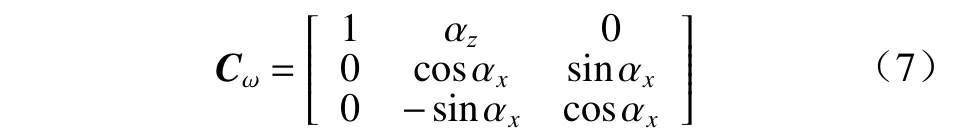
由式（6）得欧拉平台误差角微分方程

假设陀螺测量误差主要为常值漂移误差 εb和0均值高斯白噪声w，加速度计测量误差主要为常值偏置误差 ∇b和0 均值高斯白噪声w，忽略重力项 δgn，考虑到微惯性测量组合误差，由参考文献[12]可以得到初始对准滤波模型的状态方程如下

令状态向量X=[αT(δvn)T(δL)T(δh)T(δλ)T(∇b)T(εb)T]T，量测方程采用捷联惯导解算得到的位置和速度信息与卫星测量的位置和速度信息进行匹配，将两者误差作为量测值，表示为

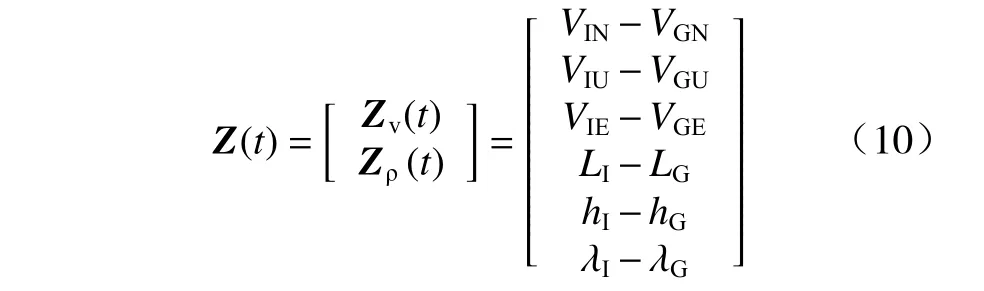
则系统状态方程和量测方程可表示为

式中：描述状态向量与微分值关系的F(X(t),t)由式（9）确 定；W(t)和V(t)分 别 为 系 统 噪 声 和 量 测 噪 声；H(t)=[06×3I6×606×6]为观测矩阵. 最后进行离散卡尔曼滤波初始对准仿真.

4 仿真验证与结果分析

4.1 系统快速初始对准原理

图8 为系统快速初始对准原理图，首先基于弹道仿真数据模拟生成了MIMU 的数据和卫星测量数据，引入实测MIMU 噪声后进行线下神经网络训练.然后在线上将卫星测量速度和捷联惯导解算速度之差以及射角传入训练好的神经网络模型预测滚转角，偏航角与俯仰角信息可以根据卫星测量速度估计[13]，误差为小量. 最后，基于扩展卡尔曼算法，利用卫星信息辅助MIMU 进行快速初始对准.

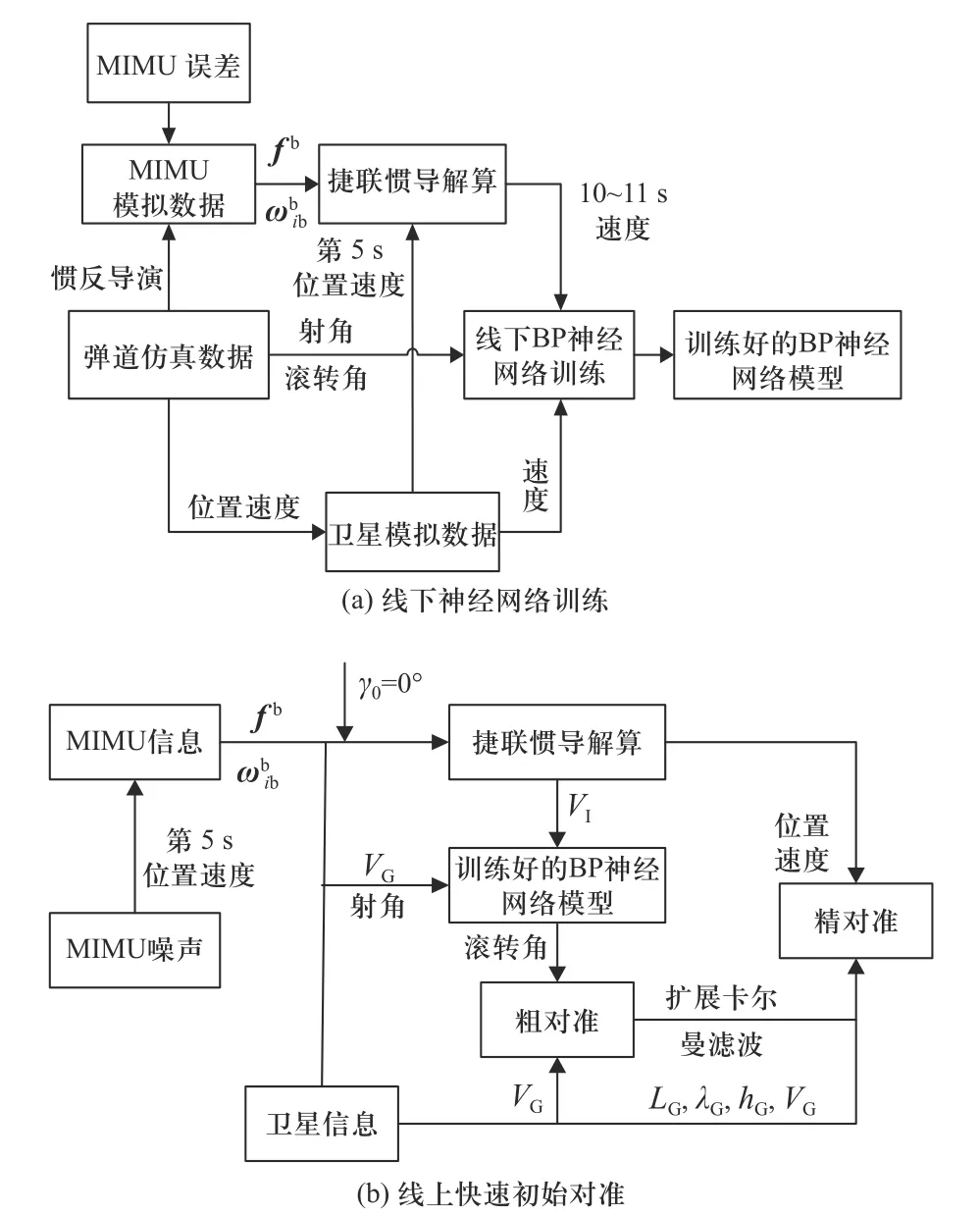
图8 系统快速初始对准原理框图Fig. 8 Block diagram of system quick initial alignment

4.2 仿真结果分析

设定仿真参数为：卫星的位置测量误差为10 m(1 σ)，速度测量误差为0.2 m/s（1 σ），MIMU 的噪声采用静止时的实测数据，其中陀螺仪随机常值漂移为25 (°)/h，加速度计随机常值偏置为2 mg，初始失准角取为[20°, 2°, 2°]. 发射后，利用MIMU 模拟数据和卫星模拟数据进行初始对准仿真.

初始对准过程中位置、速度和失准角估计误差结果如图9～图12 所示. 图9 为经过扩展卡尔曼滤波修正后的捷联惯导解算结果与真实值之差，由图9可以看出，经过对准后，位置误差能够快速收敛在0.5 m 范围内. 图10 为滤波后的速度误差结果，由图10可以看出，经过对准后，速度误差能够快速收敛在0.04 m/s 范围内. 图11 和图12 分别为失准角估计误差图和局部放大图，图中显示，弹体飞行40 s 后，3 个方向的失准角误差可以收敛到0.4°之内.

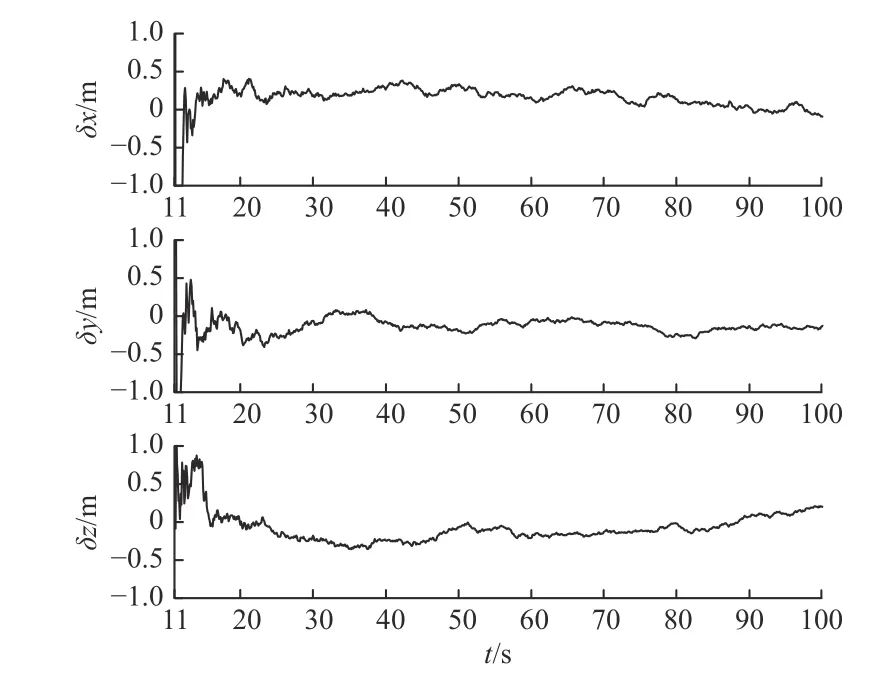
图9 位置滤波误差Fig. 9 Filter error of position

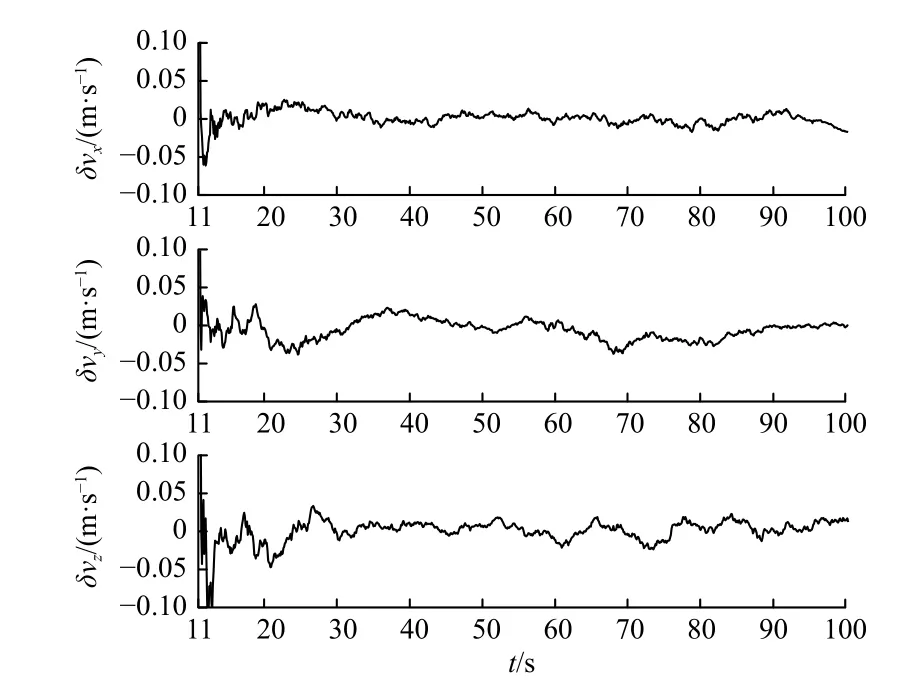
图10 速度滤波误差Fig. 10 Filter error of velocity

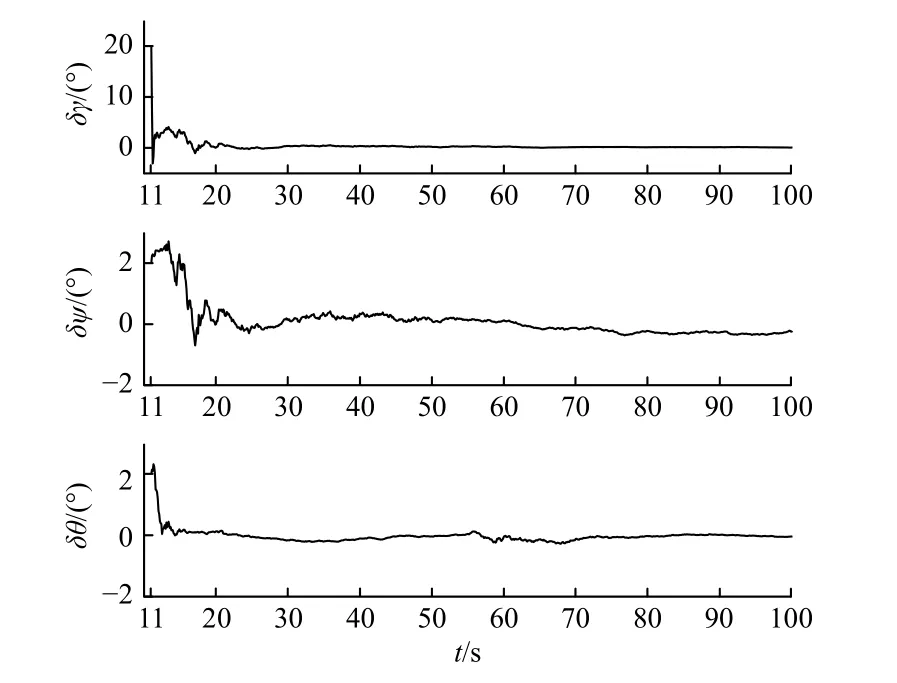
图11 失准角估计误差Fig. 11 Misalignment estimation error

5 结 论

基于不同弹道、不同滚转角下对应的捷联惯导解算速度与卫星测量速度误差之间的关系，采用BP神经网络算法，仅通过卫星和微惯性测量组合，不引入其他传感器，即可实现对双旋结构的二维弹道修正弹减旋后头部引信处滚转姿态的快速估计. 仿真结果表明，本文采用的初始对准算法能够在滚转角未知条件下估计出滚转角的粗略值，3 个方向的失准角误差在40 s 内能够收敛到0.4°之内，满足双旋结构二维弹道修正弹初始对准所需的快速性与精度的要求. 后续工作中还需要研究二维修正弹减旋后头部引信处于微旋和低旋条件下的滚转角信息获取的方法以及传感器精度对滚转角估计误差的影响.