基于霍尔传感器故障的PMSM容错控制算法

董海涛，伍兴，肖铭辰，冯建强

(广西大学 广西制造系统与先进制造技术重点实验室, 广西 南宁 530004)

0 引言

受外部环境的影响以及元器件寿命的限制，霍尔位置传感器不可避免会发生故障，导致设备无法正常运行甚至造成人员伤亡[1-2]，因此，研究永磁同步电机驱动系统的霍尔位置传感器故障的容错控制具有重要意义。

目前主要采用容错控制方案来解决霍尔位置传感器故障时的系统运行问题，主要研究方向在于故障检测，容错控制方案以及切换策略3个方面[3-5]。霍尔传感器故障检测主要分为硬件法与软件法[6-7]，国内西北工业大学的李添幸团队根据霍尔传感器的不同电气特性来判别故障类型，此方式能够较快实现故障检测，但增加系统的成本与复杂性[8]。软件检测方式相对简单且易于实现，因此广泛应用于故障检测。英国纽卡斯尔大学的Bateman在每一个电流环周期对母线电压与位置角度进行测量来实现故障检测，该方法在中高速范围能有效检测故障信号，但是不适用于低速范围的故障检测[9]。美国威斯康星大学的Harke采用一种矢量跟踪观测器来实现霍尔传感器故障检测，该方法能够消除故障瞬间的电流波动，但是在加减速方面存在不足，且霍尔信号转换需要大量计算，占用较大的资源[10]。北京科技大学的张谦团队提出一种快速故障诊断方法，该方法不需要复杂的矢量跟踪观测器运算，能够同时处理两路霍尔传感器的故障，大大提高诊断速度，但需要借助一定的辅助电路[11]。基于霍尔状态序列监测的故障诊断方法能够在较短时间内实现故障检测，成为一种实时有效的故障检测方案[12]。针对霍尔传感器故障容错控制方案，哈尔滨理工大学的吕德刚团队根据不同的霍尔传感器故障类型进行对应的相位补偿，但此方法无法实现霍尔故障状态下的容错控制[13]。西北工业大学的张希团队提出一种将霍尔信号序列特征作为诊断依据的故障诊断方法，为实现故障状态下的容错控制，建立滑模转速观测器[14]，法国学者Akrad提出一种卡尔曼滤波器与反电动势自适应观测器相结合的方法来实现电机容错控制[15]，但以上2种容错控制方法都只适用于中高速范围的容错控制，并未对低速范围的容错控制进行研究。

本文为实现全速范围内的容错控制，采用软件方式检测霍尔脉冲输出序列，判断霍尔传感器是否故障，结合脉振高频电压注入法与新型滑模观测器分别实现低速、中高速范围的容错控制。

1 容错控制策略

容错控制框架如图1所示，系统主要分为霍尔传感器模式、无传感器模式、故障检测以及模式切换4个方面。正常状态下霍尔传感器获取转子位置与速度信息，通过对霍尔序列进行检测，判断霍尔传感器是否故障。当霍尔传感器故障时，通过结合线性补偿法与加权函数，系统从霍尔传感器模式平稳切换至无传感器模式，并根据当前转子速度选择滑模观测器或脉振高频电压注入算法。

图1 容错控制框架Fig.1 Fault-tolerant control block diagram

1.1 霍尔故障检测与速度检测

霍尔传感器以等间隔120°安装在电机轴端，一个电气周期内依次输出6组霍尔信号。根据霍尔信号与电机反电动势关系来确定转子电角度，三相反电动势与霍尔信号的输出对应关系如图2所示。

霍尔位置传感器无故障时，三相霍尔按照60°电角度依次输出不同状态值，顺序为5-4-6-2-3-1。当霍尔传感器发生故障时，其对应霍尔传感器始终处于低电平或者高电平状态，由此作为霍尔故障判断条件。由图2可知，霍尔A、霍尔B、霍尔C的高低电平保持半个电气周期，当出现以下条件时，即判断为霍尔故障：三相霍尔信号出现111、000；三相霍尔组合信号未按照5-4-6-2-3-1(正转)顺序变化；三相霍尔组合信号未按照1-3-2-6-4-5(反转)顺序变化。满足上述任一条件时，系统输出霍尔故障使能信号。

为排除外部信号干扰，霍尔传感器故障检测需要判断多个霍尔扇区才使能霍尔故障信号，因此存在一定的滞后性。霍尔故障信号示意图如图3所示，假设电机H1与H2发生故障，且故障后霍尔信号维持在高电平，可以看出，在一个电气周期内霍尔组合信号只发生两次跳变。如果在此期间根据霍尔跳变信号进行测速处理，则估测速度值会发生突变，导致电机出现抖振。为了保障霍尔检测过程中电机的稳定运行，需要对测速方式进行处理。当首次检测到霍尔故障信号时，不对故障信号进行速度运算，对上一拍采样的正确速度值进行保存，根据此速度值进行扇区细分，并选择对应的无传感器容错控制算法。

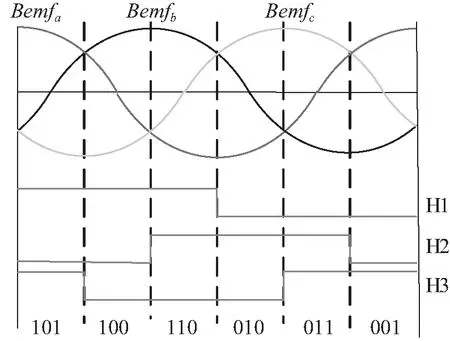
图2 三相反电动势与霍尔信号的输出Fig.2 Three-phase back electromotive force and the output of Hall signal

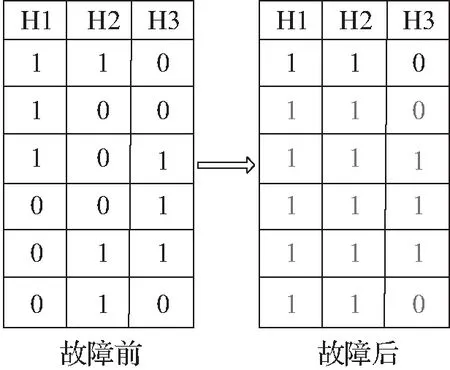
图3 霍尔故障信号示意图Fig.3 Schematic diagram of Hall fault signal

1.2 低速范围容错控制

在转子低速状态下，难以检测电机反电动势，高频电压注入法利用转子饱和凸极性可实现转子位置估测。高频载波信号是一种相对于电机转子角速度频率的高频信号，其最小频率应当与转子基波频率存在较大频谱分离空间，若接近基波频率，则载波信号不易与转子基频信号进行分离。由于电机基波频率一般在200 Hz内，本文采用的高频载波频率为0.5～2 kHz，因此其频率远远大于基波频率。

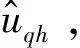
(1)

(2)

将式(2)与sinωht信号相乘，通过低通滤波处理得到转子位置误差Δθr的函数值，且在误差角度足够小时认为sin(Δθr)=Δθr，即

(3)

根据式(3)得到转子误差值信息，将其作为转子位置估测锁相环的输入，经过锁相环输出转速，再进行积分即可得到转子位置估测值。

1.3 中高速范围容错控制

滑模观测器根据定子电流与电压中包含的反电动势信息估测转子位置。基于给定电流与实际电流的误差构建滑模面，重构电机的反电动势、位置、转速信息。

将非连续性的开关符号函数作为切换函数时，会出现明显的抖振现象。本文采用具有连续性质的sigmod函数作为开关函数，定义新型滑模观测器的开关函数为

(4)

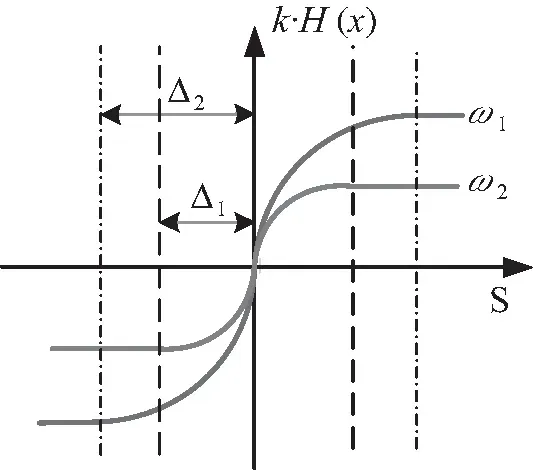
图4 滑模边界层结构Fig.4 Boundary layerstructure of sliding mode

在一个电气周期中，电机开关管的开关次数在中高速范围较低速范围少，因此，高速范围的开关效应会导致一定程度延时，系统收敛时间加大，同时伴随大量的抖振。滑膜边界层结构如图4所示，当ω1>ω2时，其对应的边界层厚度Δ1<Δ2。随着速度增大，其对应的边界层厚度也增大，系统的收敛时间也随之变大。为获得较好的滑模观测性能，要选取合适的系统增益与边界层。滑模增益系数与边界层存在关联影响，边界层厚度越小，系统精度越高，间接影响增益系数。

由图4可知，不同a值的边界层厚度一定，当a值一定时，增加增益系数可提高系统的响应速度，所以在高速区域要调整系统增益系数。本文采用与转子角频率正比的开关增益系数。

k=ks×ω。

(5)

根据Lyapunov稳定性定理，k=ks×ω需要满足：

k≥max(eα,eβ)。

(6)

则新型的SMO模型为

(7)

式中:k为滑模的变增益系数；H为sigmod函数，其表达式为

(8)

将式(8)与式(7)相减，得到定子电流的误差方程为

(9)

(10)

对等效控制量低通滤波后，通过正反切函数方法获得转子位置信息与速度信息。

(11)

新型滑模观测器框图如图5所示，将α-β坐标系的电压和电流作为状态输入量，得到滑模观测电流，同时与电机反馈电流进行比较，经过切换函数处理后，观测出电机的反电动势。

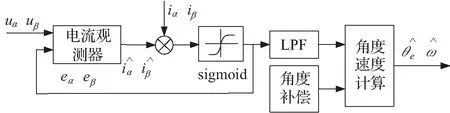
图5 新型滑模观测器框图Fig.5 Block diagram of the new sliding mode observer

2 容错控制切换策略

图6 速度区间划分示意图 Fig.6 Schematic diagram of division of speed zones

脉振高频电压注入法适用于电机零速与低速范围的转子位置估测，滑模观测器适用于中高速范围的转子位置估测。为了实现霍尔传感器故障时算法的平滑切换，需要将2种无传感器算法进行结合，实现电机低速至中高速范围的模式平滑切换。根据2种无传感器算法的适用特性，采用加权函数方法实现速度过渡区间的衔接。速度区间划分示意图如图6所示，当电机转速ω>ω2时，采用滑模观测器估测转子位置，ω<ω1时采用脉振高频法估测转子位置，ω1≤ω≤ω1时2种算法在加权函数下共同作用。

为了在故障时实现2种模式的平稳切换，采用加权函数来对无传感器模式的2种算法进行整合，如式(12)所示。

(12)

式中n为加权因子，通过加权因子得到无传感器模式中的电角度值，如式(13)所示。

θ3=nθ1+(1-n)θ2，

(13)

图7 模式切换补偿示意图Fig.7 Schematic diagram of modeswitching compensation

式中:θ1为脉振高频算法估测电角度；θ2为滑模算法估测电角度；θ3为加权函数处理后无传感器模式估测电角度。

一旦系统检测到霍尔故障信号，将自动从有传感器模式切换至无传感器模式，无传感器算法得到的电角度θ3与霍尔传感器输出的电角度θ4存在误差，模式切换补偿示意图如图7所示。

将θ3与θ4做差得到误差值Δθ=θ4-θ3，该误差值会造成较大的转矩脉动，需要对此误差值进行均分处理，依次在电流环运算中进行补偿，如式(14)所示，θ为补偿电角度值。

(14)

3 实验

为了验证容错控制算法性能，搭建PMSM容错控制模型，PMSM参数见表1。

表1 PMSM参数Tab.1 PMSM parameters

为了验证新型滑模观测器算法的速度估测精度，在滑模观测器模型中进行速度对比实验。滑模观测器速度对比曲线如图8所示将电机速度给设定为1 000 r/min，根据图8可以看出新型滑模观测器在0.01 s达到稳定，估测转速与实际转速误差在10 r/min内，可见新型滑模观测器能够精确估测转子当前转速。

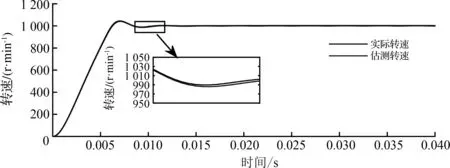
图8 滑模观测器速度对比曲线Fig.8 Comparison curve of the speed of the sliding mode observer

新型滑模观测器估测的转子估测位置与实际位置曲线如图9所示，由图9可见滑模观测器的电角度观测准确，与电机实际电角度基本吻合。由于滑模观测过程中使用低通滤波器，相位角度出现10°延迟，因此在电角度误差图中存在360°误差。

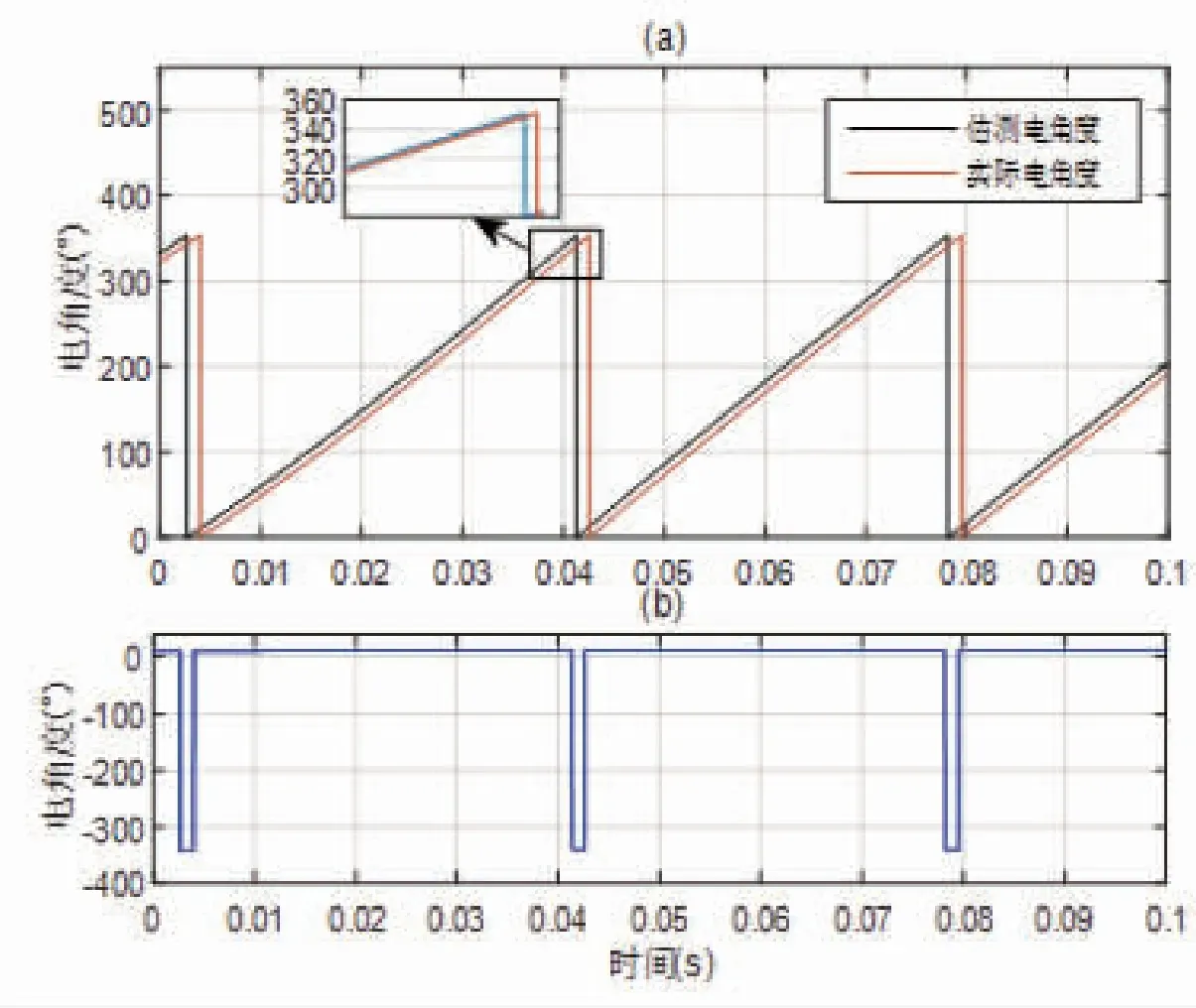
图9 转子估测位置与实际位置曲线Fig.9 Curves of estimated position and real position of rotor

对低速状态下容错控制策略的性能进行验证，首先采用霍尔传感器模式设定电机转速为100 r/min，在0.15 s处输出霍尔故障使能信号，将霍尔传感器运行模式切换至脉振高频无传感器控制模式。低速范围容错控制模式切换曲线如图10所示，由图10(a)可见，电机在0～0.15 s内采用霍尔传感器运行模式，速度响应无明显波动。0.15 s时加入霍尔传感器故障信号，控制系统切换至脉振高频无传感器控制模式，转子速度在经过0.03 s的小幅度抖振后迅速稳定至100 r/min,速度波动在±5 r/min内。图10(b)为低速范围容错控制转子电角度曲线，0～0.15 s内转子电角度平稳，0.15 s时进行故障模式切换，脉振高频电压注入法估测电角度与转子当前电角度存在10°差值，切换时，转子经过0.03 s的抖振后顺利切换至无传感器控制模式。由图10可知，脉振高频电压注入法能够精确获取低速状态下的转子位置信息，同时能够实现低速范围的模式切换。

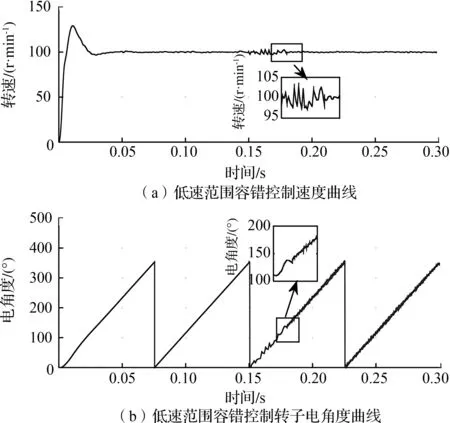
图10 低速范围容错控制模式切换曲线Fig.10 Switching curve of fault-tolerant control mode in low-speed range

为了验证中高速状态下容错控制性能，在霍尔位置传感器模式下，给定电机转速为1 000 r/min， 在0.2 s处输出霍尔故障使能信号，将霍尔传感器运行模式切换至滑模观测器无传感器模式。中高速范围容错控制模式切换曲线如图11所示，由图11(a)可知相对于低速运行状态，中高速范围的转子位置更易于估测，在0.2 s时转子速度波动范围为±10 r/min。由图11(b)可知，在模式切换时刻，滑模观测电角度与霍尔位置估测电角度误差在10°附近波动，因此，在中高速范围霍尔传感器模式与无传感器模式能够平稳切换。

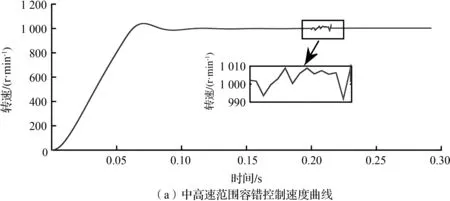
图11 中高速范围容错控制模式切换曲线Fig.11 The switching curve of the fault-tolerant control mode in medium and high speed range

图12所示为容错控制模式速度曲线。由图12可见，在0～0.05 s内电机处于霍尔传感器运行模式，转子速度为1 000 r/min，0.05 s时加入霍尔故障使能信号，经过0.05 s的抖振后速度曲线趋于平稳，相较于有传感器模式，速度存在一定的波动与抖振。0.1 s时，给定电机速度为100 r/min，在脉振高频电压注入法的作用下，电机速度曲线稳定在100 r/min，且无明显波动。

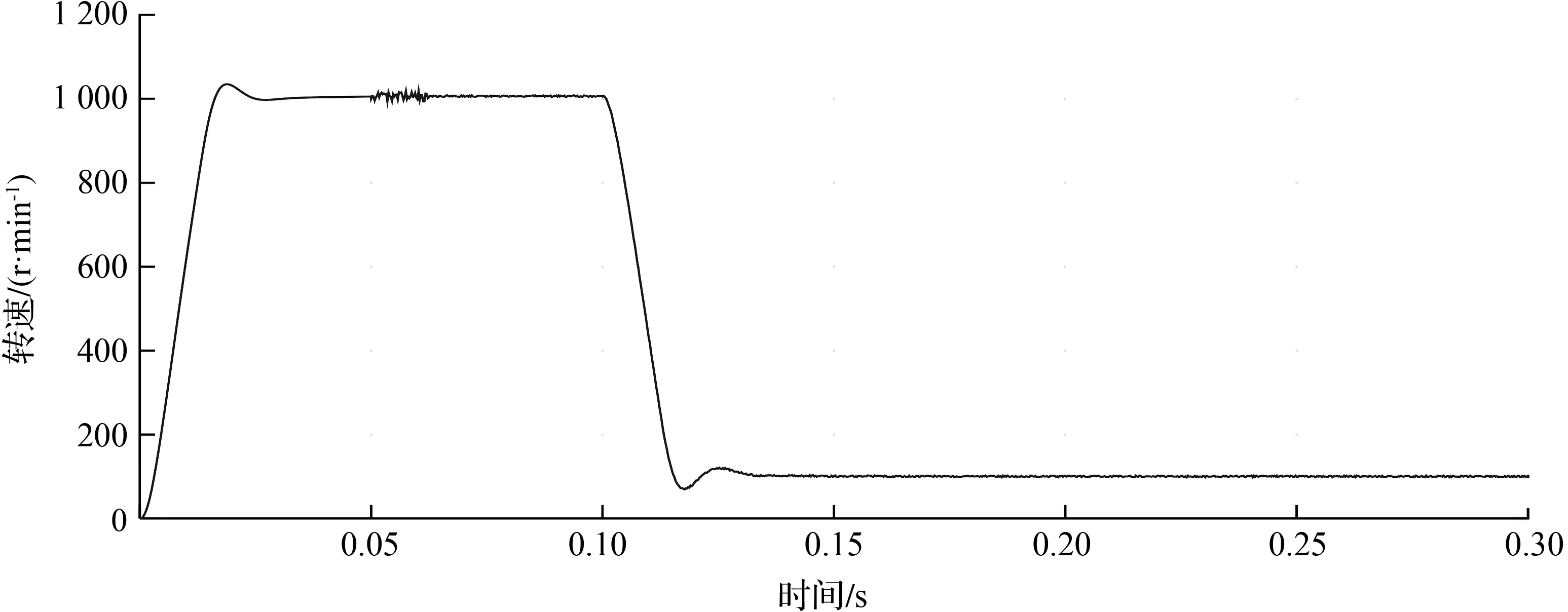
图12 容错控制模式速度曲线Fig.12 Speed curve of fault-tolerant control mode

图13 道闸控制平台Fig.13 Barrier control platform

图13所示为实验用道闸控制平台。对所提出的容错控制算法分别在低速、中高速和中高速切换至低速3个阶段进行了实验。实验结果表明：道闸能够在3 s内完成一次抬杆或放杆动作，运行过程无抖动、砸杆等现象，拔掉霍尔传感器的信号线时，控制能够自动平稳切换到无传感器模式，运动平稳，控制效果较好。

4 结论

本文针对永磁同步电机的霍尔信号故障，结合无传感器控制技术，提出电机全速范围的容错控制策略。霍尔传感器正常情况下，采用有感控制模式，当发生故障时，采用脉振高频电压注入法与滑模观测器切换至无感控制模式，并结合线性补偿法与加权函数减少模式切换过程中的抖振现象。实验结果表明，该容错控制算法能够实现全速范围霍尔传感器模式与无传感器模式的切换，保证电机在霍尔传感器故障状态下的稳定运行。