基于Bootstrap方法的厚尾AR(p)序列均值变点检验

乔 瑞，杨云锋，金 浩

(西安科技大学 理学院，陕西 西安 710054)

0 引 言

变点检验对于决策者们具有重要的现实意义,若忽略变点的存在,则会导致错误的建模,从而做出错误的决策,造成一定的风险.为了规避风险,应用统计方法对变点进行统计推断就显得尤为重要.在变点检验的各种问题中,均值变点检验在变点问题的分析中占据了非常重要的地位.Gardner[1]讨论了方差为1时的独立高斯序列均值变点检验.随后Sen等[2]修正了Gardner[1]的检验统计量,在方差未知时探讨了高斯序列的均值变点问题.Chen等[3]基于比值型监测统计量监测了长记忆时间序列的均值变点和方差变点,发现此检验在越靠近监测开始时间时具有更好的有限样本性能.Lebarbier[4]基于惩罚最小二乘估计方法对高斯序列的多均值变点进行了估计.韩四儿等[5]在累积和统计量的基础上,提出拟似然比方法对多均值变点进行检验.齐培艳等[6]研究了非参数回归模型基于小波系数的均值变点的在线监测问题.与传统的Kolmogorov-Smirnov检验以及“滑窗”检验方法相比,自正则的K-S检验可以避免窗宽参数的选取,因此潘婉彬等[7]采用基于自正则的K-S方法对羊群行为的均值变点进行了检验.

以上的均值变点检验问题的模型的新息过程都是高斯序列,要求方差存在.但随着越来越多的高频数据的出现,例如环境、工业等数据都呈现出尖峰厚尾特征,它们的尾部存在很多异常值,导致大部分信息滞留在尾部,常规的高斯序列已经无法对其进行描述,而厚尾序列恰好可以刻画这类数据的特征.因此,对厚尾序列变点的统计推断是必不可少的.这一内容吸引了一众统计学家和计量经济学家对其进行研究.刘舰东等[8]利用累积和统计量研究了方差无穷的ARCH序列均值变点的检验问题.针对检验统计量依赖未知尾指数的现象,Jin等[9]采用Bootstrap子抽样方法检测了厚尾序列的均值变点.Wang等[10]通过利用Bootstrap抽样分布来逼近检验统计量的极限分布,以实现厚尾序列均值变点的检验和估计.Zhou等[11]基于加权最小二乘估计法构造加权累积和统计量推断了厚尾序列的均值变点,其检验统计量的极限分布不依赖于未知的厚尾指数.更多关于厚尾序列变点的研究,可参见文献[12-14].

基于Ratio统计量将Jin等[9]对独立同分布的厚尾序列均值变点检验拓展到一般的AR(p)模型.由于检验功效易受变点位置的影响,通过颠倒统计量重新构造出新的Ratio统计量来弥补此缺陷.另外,考虑到统计量的极限分布依赖于未知的尾指数,利用Bootstrap抽样方法来逼近统计量的极限分布从而实现厚尾序列均值变点的检验.

1 模型与假设

考虑新息过程为AR(p)过程的均值变点模型:

yt=μ+Δ·I{t>k*}+εt

(1)

εt=ρ1εt-1+…+ρpεt-p+ηt,t=1,…,T

(2)

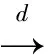
这里考虑假设检验问题:

H0:Δ=0

H1:在未知的时刻k*,Δ≠0

下面给出本文所需的假设和引理:

假设1假设特征多项式ρ(z)=1-ρ1z-…-ρpzp的根都在单位圆之外.

假设2{ηt}∈D(κ),这里D(κ)为尾指数κ∈(1,2]的稳定吸收域,且Eηt=0.

引理1如果{ηt}是独立同分布序列,且满足假设2,则:

其中L1(r)和L2(r)分别是在[0,1]上的κ-Lévy过程和κ/2-Lévy过程.Kokoszka等[15]进一步证明aT可以简化为aT=T-κ(T).L1(·)是一个稳定过程,其可以表达为:

这里{Ut}是独立同分布在区间[0,1]上的均匀分布随机变量,{δt}是独立同分布的随机变量,满足P(δt=1)=1-q,P(δt=-1)=q.Γ1,Γ2,…是具有勒贝格测度的泊松过程的到达时间,且{Ut,δt,Γt}相互独立.

经典的累积和统计量已被广泛用来检测均值变点,但累积和统计量需要通过序列的长期方差来标准化,特别是在新息过程是相依的情形下.Breiman[16]和Antoch等[17]指出找到具有良好性质的长期方差估计量是极其困难的,即使在独立情形下,长期方差估计量也常常表现不佳,在备择假设下显得尤为突出.因此,Horváth等[18]提出了Ratio统计量:

(3)

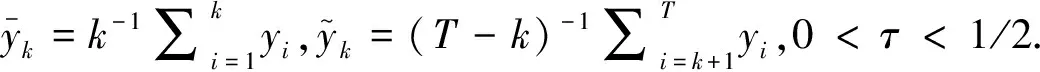
定义新的Ratio检验统计量如下:

2 主要结论

下面给出统计量在原假设下的极限分布及在备择假设下的一致性.

定理1若随机序列{yt}由(1)～(2)生成,{εt}是厚尾AR(p)过程,且假设1～2成立,在原假设H0下,当T→∞时,有:

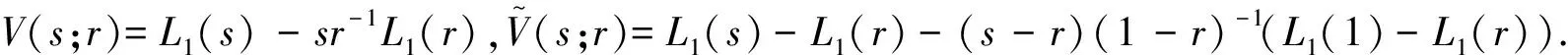
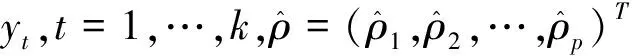
(4)

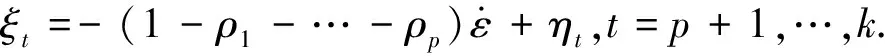
则式(4)可写为矩阵形式:

G=Jρ+ξ

因此,ρ的最小二乘估计为:

(5)

将G=Jρ+ξ代入式(5),则:

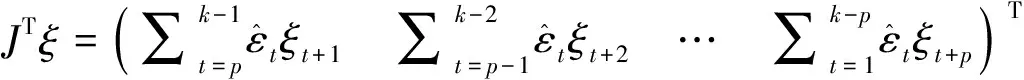
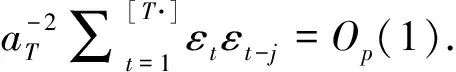
(6)

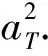
(7)

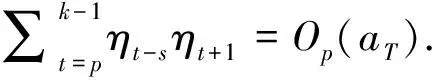
令：

联立式(6)和(7),则:

(8)

对于t=p+1,…,k,有：

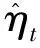
则：

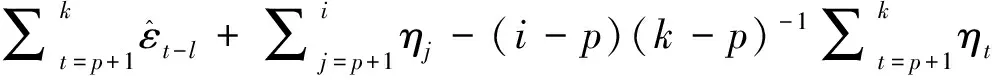
(9)

同理可证得:

(10)

定理1表明修正的Ratio统计量R*在原假设下的极限分布是Lévy过程的泛函.下面给出备择假设下统计量的一致性结论.

定理2若随机序列{yt}由(1)～(2)生成,{εt}是厚尾AR(p)过程,且假设1～2成立,在备择假设H1下,当T→∞时：

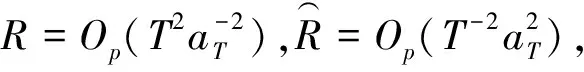
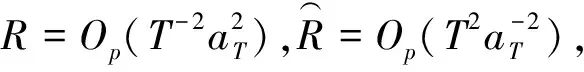
证明当k*≤k时,基于样本yt,t=1,…,k,得到残差:

(11)

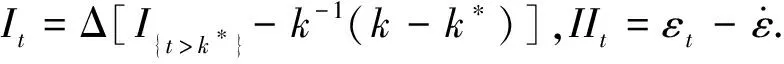
(12)

将式(11)代入式(2),有:

其中:

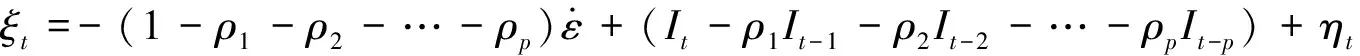
(13)

因式(13)的第二项不是随机变量,再次利用BN分解,得:

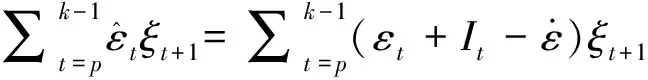
=Op(T)

(14)

令：

根据定理1的证明,结合式(12)和式(14),有:

(15)

因此,当t=p+1,…,k时：

则:

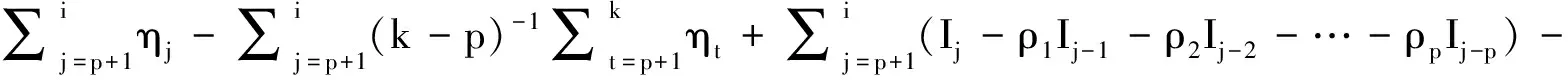
令i=[Ts],k=[Tr],k*=[Tr*],当k*≤k时,有:

=3-1r*2(r-r*)2r-1Δ2(1-ρ1-…-ρp)2

和

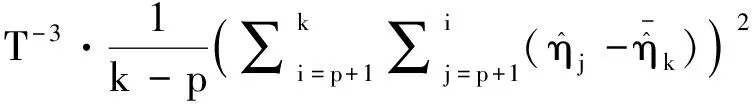
=4-1r*2(r-r*)2r-1Δ2(1-ρ1-…-ρp)2.

从而容易推出:

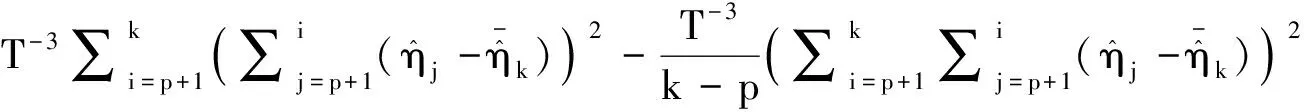
由于样本yt,t=k+1,…,T不包含均值变点,则统计量分母的极限分布与其在原假设下的极限分布相一致.因此,(i)得证.类似的,(ii)同理可证.则定理2证毕.

定理2证明了Ratio统计量在备择假设下的一致性.不难发现,统计量的发散速度随着厚尾指数κ,样本容量T、跳跃幅度Δ的增大而增大.特别地,若p=1,则发散速度随着回归系数ρ1的减小而增大.

统计量的极限分布依赖于未知的尾指数κ,Mandelbrot[20]提出了一个粗略的方法来估计厚尾指数κ,但精确性不令人满意.为了避免干扰参数κ的估计,利用Bootstrap抽样方法来逼近原假设下统计量的极限分布以获取精确的临界值.具体步骤如下:

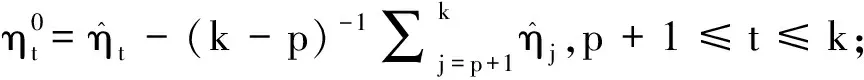
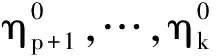
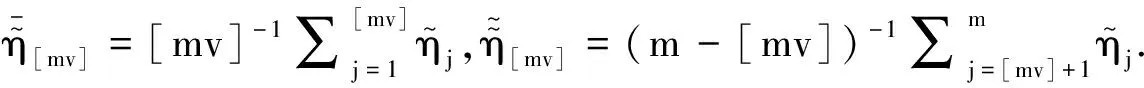
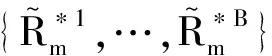
选择一个通用的m使得其在任何情况下都是最优的难以实现,但Mcmurry等[21]提供了控制经验水平和经验势的一个理想选择m=[4T/ln(T)].因此,在数值模拟中这个子样本m也将继续沿用.

3 数值模拟

本节通过蒙特卡洛数值模拟验证基于Bootstrap方法的Ratio检验的有效性.考虑一阶自回归单均值变点模型:yt=μ+Δ·I{t>k*}+εt,εt=ρ1εt-1+ηt,其中{ηt}是零期望独立同分布厚尾序列.先利用Bootstrap抽样方法确定统计量的临界值.不失一般性,设定显著性水平α=0.05,厚尾指数κ={1.1,…,2},循环次数为B=3 000,样本容量为T=2 000,均值μ=0,回归系数ρ1={-0.5,0,0.5}.模拟结果均通过Matlab软件实现.

表1 基于Bootstrap的Ratio统计量临界值,T=2 000

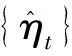
为了进一步说明Ratio检验统计量的检验功效,设定跳跃幅度Δ={0,2,4},变点时刻r*={0.3,0.7},样本容量T={300,500,1 000},并用 3 000 次试验中拒绝原假设的百分数作为经验势函数值.图1所有的蓝线表示回归系数ρ1=-0.5的统计量的拒绝率,绿线表示ρ1=0时的拒绝率,红线表示ρ1=0.5时的拒绝率,实线表示R,虚线表示R*,横坐标为厚尾指数κ,纵坐标为拒绝率.

图1表示原假设下原统计量R和重新构造的统计量R*的拒绝率.由图中可以看出,当样本容量增大时,拒绝率越来越接近显著性水平0.05,且在其附近的波动越来越小;厚尾指数、回归系数的变化几乎不影响Ratio检验统计量的拒绝率.这说明基于Bootstrap方法的Ratio检验统计量很好地控制了经验水平.

(a)样本T=300 (b)样本T=500 (c)样本T=1 000图1 原假设下Ratio检验的拒绝率Fig.1 The rejection rate of Ratio test under the null hypothesis

图2～图3表示备择假设下跳跃幅度Δ=2,变点时刻r*={0.3,0.7}的原统计量R和重新构造的统计量R*的拒绝率.随着样本容量的增大,统计量的拒绝率增大,这与定理2的结论相吻合,即样本容量越大统计量发散程度越大.当厚尾指数κ减小时,统计量的拒绝率减小.这是由于随着厚尾指数κ越小,序列包含的异常值会增多,导致临界值越大,出现难以拒绝原假设的现象，从而使得拒绝率减小.此外,κ越小,备择假设下统计量的发散速度越慢,这说明了κ越小,拒绝率越低的合理性.当回归系数ρ1=-0.5时,拒绝率最大,回归系数ρ1=0次之,回归系数ρ1=0.5时,拒绝率最小.这可以从定理2的结论中得出,ρ1越小,统计量越发散,拒绝率越高.

图2表明当r*=0.3时,原统计量R比重新构造的统计量R*的拒绝率略高,这说明若变点时刻位于样本前半段,原统计量R较容易检测到变点,但两者之间的差异不大.但由图3可以看出,若变点时刻位于样本后半段r*=0.7时,重新构造的统计量R*的拒绝率远高于原统计量R的拒绝率,且两者之间差异愈加明显.这恰好印证了本文所提检验统计量的优势.根本原因是相比原统计量的检验依赖于变点位置,重新构造的Ratio检验统计量的经验势不会因变点时刻位于样本后半段而大幅度降低,从而减弱检验功效.

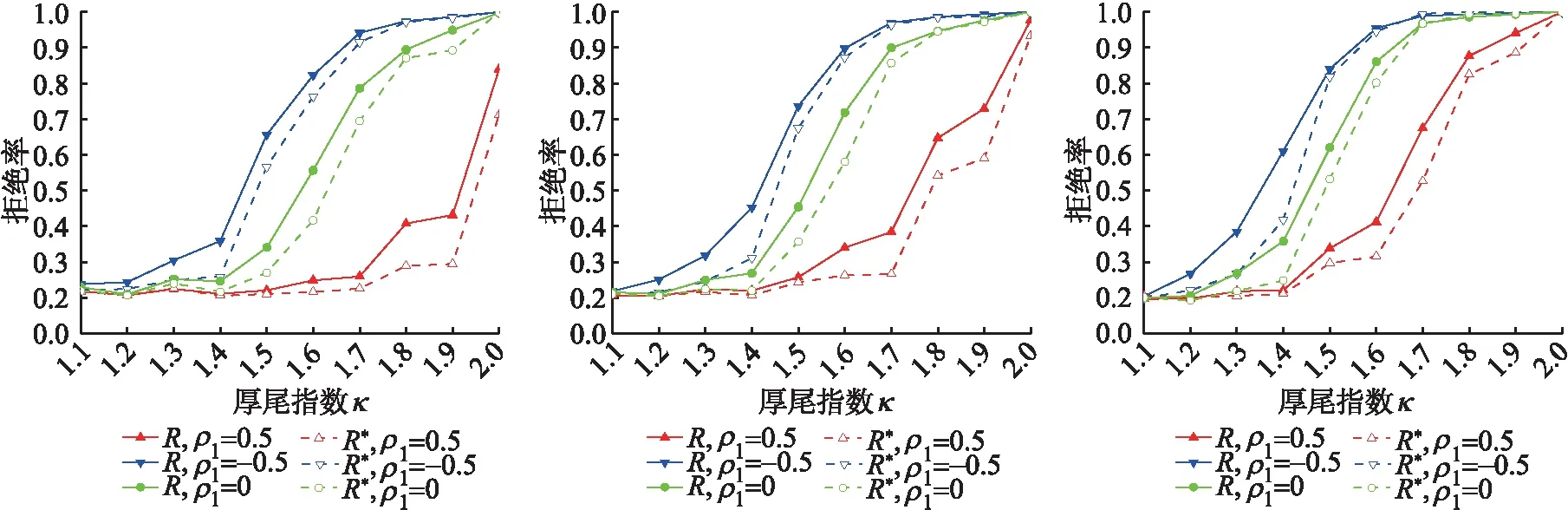
(a)样本T=300 (b)样本T=500 (c)样本T=1 000图2 备择假设下Ratio检验的拒绝率,r*=0.3,Δ=2Fig.2 The rejection rate of Ratio test under the alternative hypothesis,r*=0.3,Δ=2

(a)样本T=300 (b)样本T=500 (c)样本T=1 000图3 备择假设下Ratio检验拒绝率,r*=0.7,Δ=2Fig.3 Ratio test rejection rate under the alternative hypothesis,r*=0.7,Δ=2

图4～图5表示备择假设下跳跃幅度Δ=4,变点时刻r*={0.3,0.7}的原统计量R和重新构造的统计量R*的拒绝率.正如所期望的,统计量的检验功效依赖于跳跃幅度Δ,当跳跃幅度增大时,统计量的拒绝率出现了明显的增大.与Δ=2的情况类似,随着样本容量、厚尾指数的增大,统计量的拒绝率增大,但回归系数越大统计量的拒绝率越小.总之,相比于原统计量R对变点在样本后半段检验不显著的缺陷,重新构造的统计量R*的检验显著性不受变点位置的影响.这表明基于Bootstrap方法的Ratio检验为检测厚尾相依序列均值变点提供了一种行之有效的工具.

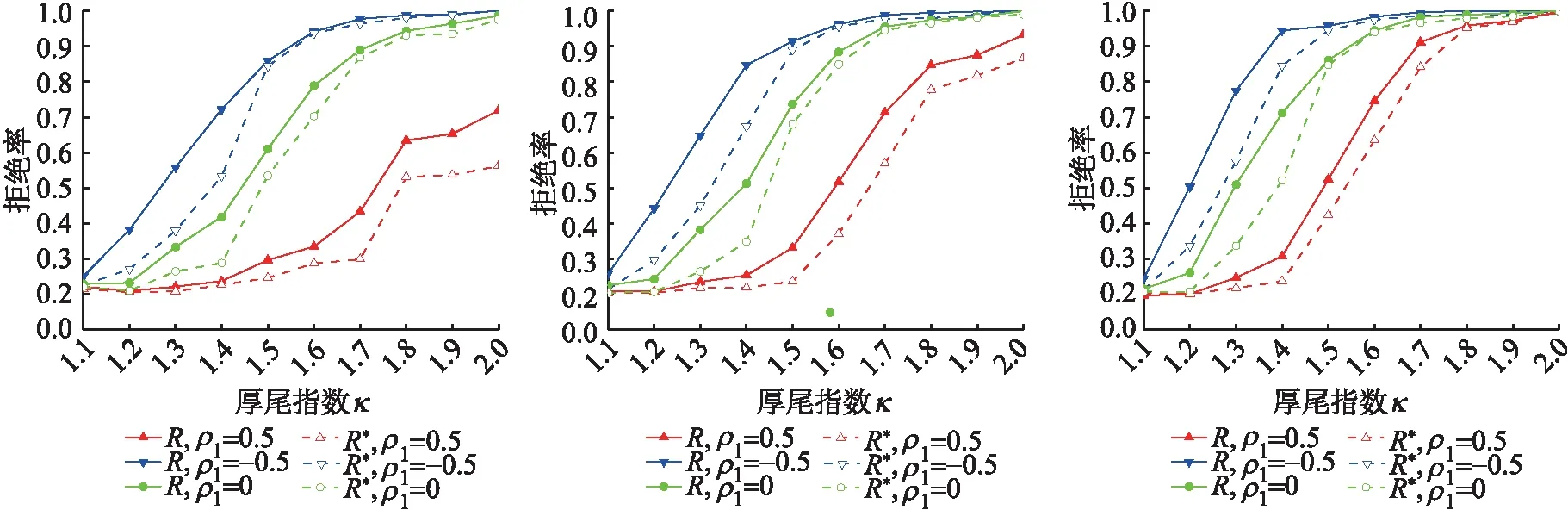
(a)样本T=300 (b)样本T=500 (c)样本T=1 000图4 备择假设下Ratio检验拒绝率,r*=0.3,Δ=4 Fig.4 Ratio test rejection rate under the alternative hypothesis,r*=0.3,Δ=4

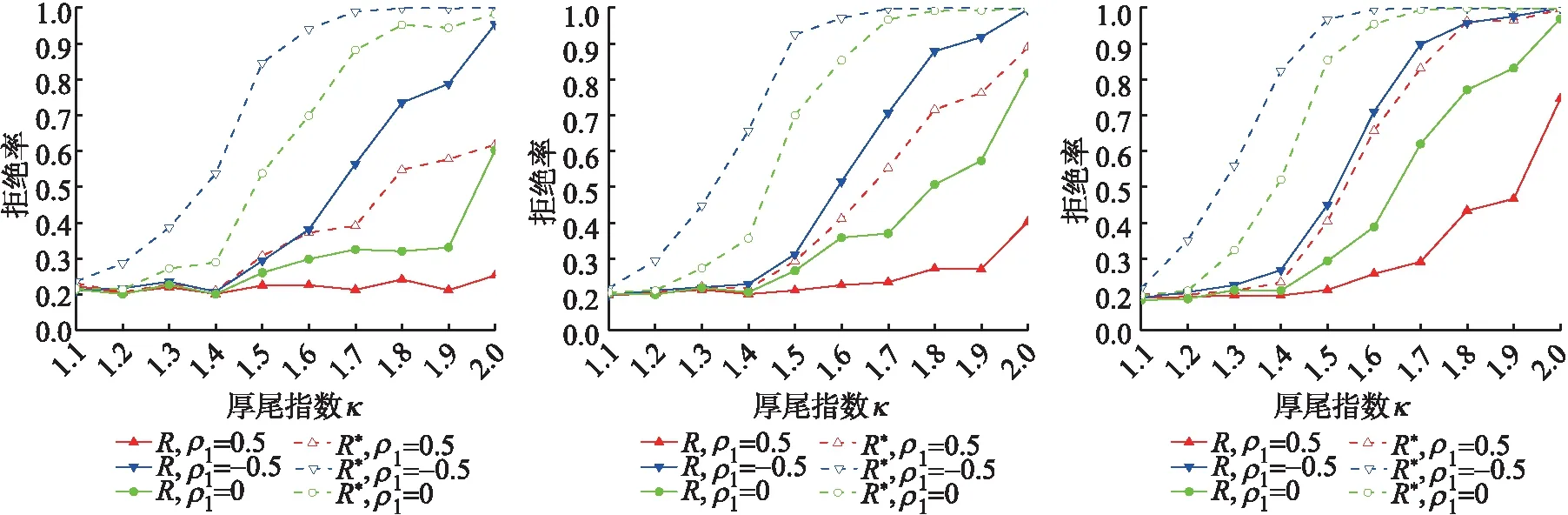
(a)样本T=300 (b)样本T=500 (c)样本T=1 000图5 备择假设下Ratio检验拒绝率,r*=0.7,Δ=4 Fig.5 Ratio test rejection rate under the alternative hypothesis,r*=0.7,Δ=4

4 结 论

本文基于Bootstrap方法检测了厚尾自回归过程的均值变点.为提升检验功效,通过颠倒统计量重新构造出新的Ratio检验统计量,在原假设下推导了检验统计量的极限分布为Lévy过程的泛函,并给出了备择假设下的一致性.为了避免厚尾指数的估计,Bootstrap抽样方法被用来确定更精确的临界值.最后由蒙特卡洛数值模拟验证了基于Bootstrap方法的Ratio检验的有效性和可行性.