井下地磁匹配数据的小波降噪性能研究

汪金花，杨华文，李鸣铎,2，刘暑明

(1.华北理工大学 矿业工程学院，河北 唐山，063210; 2.华北理工大学 电气工程学院，河北 唐山，063210)

0 引 言

近几年，地磁定位或地磁组合定位技术逐渐在室内、地下空间智能导航领域开始兴起[1-2]，出现了PDR和地磁融合室内定位[3]，地磁和WIFI组合定位[4]，地磁与RFID组合的GRPM定位等的相关研究[5].关于半封闭空间、构建物内部或地下工程的内部磁场特征，国内外一些学者进行了研究.结果表明，室内或地下工程内多种磁场叠加效应[6]，包括天然地磁场、混凝土、钢筋支护等材料产生的磁场，及内部的管道、通信设备等产生的磁场等等.同时发现这些地磁定位优势明显，空间点的地磁特征存在差异.但是实测磁数据不可避免地存在噪声，含有较大的常值噪声和随机噪声，其数值会随着空域、时域变化发生扰动.另外一些研究发现测量地磁数据时，其工作周边环境变化也会产生数值较大磁扰动或磁噪声.汪金花等[7]研究了井下罐笼升降对附近点位磁噪声的扰动幅度和扰动时长，发现罐笼运动主要强噪声扰动时间一般在10 s以内，扰动数值约几百至上千纳特之间.毛君等[8]研究AKF地磁辅助导航的采煤机定位方法时，发现采煤机工作时的井下环境地磁场的变化特征具有一定的复杂性.这些时域和环境噪声数值大小不稳定，难以用统一数学模型修正，其隐含在磁数值中不易发现.在地磁指纹匹配定位时，容易导致地磁定位失败或者降低地磁定位精准度.为此一些学者采用空域、频域等多种方法进行磁数据降噪研究，来提高地磁匹配定位的精度.汪金花等[7]针对井下运输车、罐笼运动对附近点位磁扰动，采用中值滤波或小波阈值去噪的方法进行处理，达到减弱匹配数据中的瞬间强噪声目的.谢凡等[9]研究发现轨道交通会干扰实测地磁值，运用小波噪声阈值方法抑制模型噪声，达到消噪结果.康瑞清等[10-11]针对实测地磁数据的软噪声和硬磁干扰，发现经验模态分解的阈值滤波方法能够降低的匹配误差最低，可以有效提高车辆导航的精度.汪金花等[12]采用Laplace、High pass和Sobel卷积算子构建了井下磁数值CEA卷积算子，试验发现CEA算子卷积后增强匹配序列和地磁图的地磁空间特征，降低了磁噪声扰动的影响.文中针对地磁匹配的磁基准数据，进行傅立叶滤波和小波阈值去噪对比试验，并对不同噪声水平下小波去噪性能效果进行测试量化分析，研究地磁数据的小波去噪方法的可靠性.

1 井下地磁匹配的降噪

1.1 井下地磁噪声扰动

假设实际采集地磁数据是将磁通门计的初始地磁值(定标数值)设定为区域稳定场，实际测量每个空间点的地磁值就是区域磁异常.磁力仪所采集数值与该点磁异常场值差值称为磁扰动ET.它受到地磁的“日变”场、周围环境产生的磁场、磁力仪测量磁噪声等多种因素影响:

ET=Bi-g(xi,yi)=△gi+△ei+mi

(1)

式中：Bi为定位时磁力仪测得磁场强度；g(xi,yi)为空间点(xi,yi)的磁异常场值，后文简称磁场值；△gi为空间点(xi,yi)磁数值随时间变化磁扰动；△ei为随环境变化磁场扰动值.△ei为随机常值和一个高斯白噪声组合误差，包含模型误差、测量误差，是影响地磁匹配算法匹配精度的主要原因[13]；mi为磁力仪测量磁噪声，磁力仪载体的干扰场，如人员行走对地磁测量影响值.

地磁点磁总值的时域变化是相对较小的，约几百纳特，这些磁扰动主要是“日变”的周期波动值，数值扰动总体均值是一个相对的固定值，且服从高斯分布.周边环境磁扰动会产生随机噪声，随机噪声的大小是不确定的，例如人员行走对点位磁总值的影响就较小，最多是几百纳特，而距离点位较近的罐笼升降则对点位磁总值的影响较大，会产生几千至上万纳特的噪声，如图1所示.地磁匹配是依据待匹配数据与基准数据特征的相似度进行定位的.当进行地磁匹配时，这些时域和环境磁噪声都会叠加到实时测量磁序列中，会造成磁数值序列偏移，直接影响地磁匹配定位结果的精准度.

图1 点位周边环境变化造成的磁扰动Fig.1 Magnetic disturbance caused by environmental changes around the point

1.2 地磁数据降噪方法

地磁数据是地磁匹配定位的依据，在采集过程中难以避免受到噪声污染，成为匹配定位的含噪地磁信息.可以通过傅立叶变换法和小波分析方法来对目标区域的地磁数值进行去噪处理，提高地磁匹配成功概率的目的.

1.2.1 傅立叶变换降噪

傅立叶变换去噪法的基本思想是对含噪图像数据进行傅立叶变换后使用Butterworth低通滤波器滤除噪声频率，然后再用傅立叶逆变换恢复图像.傅立叶变换能比较彻底地去除高频噪声，但是很难将有用的高频部分和由噪声引起的高频干扰区分开.

二维离散傅立叶变换公式如下：

(2)

式中：f(x,y)是大小为M×N的数字图像.

Butterworth低通滤波器的定义如下:

(3)

(4)

二维离散傅立叶逆变换公式如下：

(5)

1.2.2 小波阈值降噪

小波变换具有时频局部化特性、多分辨特性、去相关特性和选基灵活性[14].时频局部化特性和多分辨特性决定了小波去噪方法与传统去噪方法相比具有独特的优势.小波去噪方法能够对图像数据进行有效去噪，同时还能很好地保留图像的边缘特征.

经小波分解后的含噪数据，其信号的系数要大于噪声的系数，所以可以选择一个合适的λ作为阈值[15]，当分解系数小于这个临界阈值时，认为分解系数主要为噪声，将其舍弃，分解系数大于这个临界阈值时，认为分解系数主要为信号，将其直接保留(硬阈值方法)或按照某一固定量向零收缩(软阈值方法)，然后用得到的小波系数进行小波重构，即为去噪后的信号.文中选用软阈值函数.

阈值λ计算式为：

(6)

软阈值函数为：

(7)

阈值去噪对信号分解小波系数进行处理来达到去噪的目的.数理过程需要确定阈值函数和具体阈值大小.如何选取阈值函数和如何对阈值进行量化是阈值去噪最重要的环节，由于噪声是一种随机信号，其方差是未知的，实际去噪过程中必须首先对阈值进行估计.基于样本估计的阈值的选取，其原理是通过信号估计来确定一个具体的阈值，通常有默认阈值wav-R1、自适应阈值wav-R2及极大极小阈值wav-R3的小波去噪处理，其中：

2 试验方法

2.1 试验方案

地磁数据受到区域性、时域性和噪声综合影响，通常实测地磁数值均会有噪声扰动，噪声最小为十几纳特，最大可达上万纳特.特别是在地磁特征变化缓慢的区域内，大噪声的干扰会淹没了这块区域实际地磁的微小变化，直接导致匹配结果的虚定位.试验针对不确定地磁噪声水平情况下，傅立叶变换和小波变换降噪效果.同是测试不同阈值小波降噪效果差异性，检测高噪声水平下小波降噪可行性.

设测得的数据fi为无噪数据，为fi添加叠加性高斯白噪声，设添加噪声后的地磁数据为yi：

yi=fi+kzi,i=1,2,…,N

(8)

式中：zi为独立分布的高斯白噪声N(0,1)，k为噪声水平，N为信号长度.

2.2 数据来源

试验选取了4个带状区域开展地磁测量试验分析[16-17]，测区周边建筑为钢筋混凝土加固，部分区域有输电设备.4块带状区域分别命名为BPT-1、BPT-2、BPT-3和BPT-4.各采集区域长度和宽度相同，长度为40 m，宽度为2.4 m，每块区域布设5条控制线，间隔为0.6 m，每条线上间隔0.6 m设置一个采样点.地磁测量采用便携式 FVM-400 磁通门磁力仪，量程为 100 000 nT，分辨率可达1 nT.测量噪声方差为 50 nT2，测量随机常值误差为10～30 nT，符合小区域高精度地磁场的测量要求.

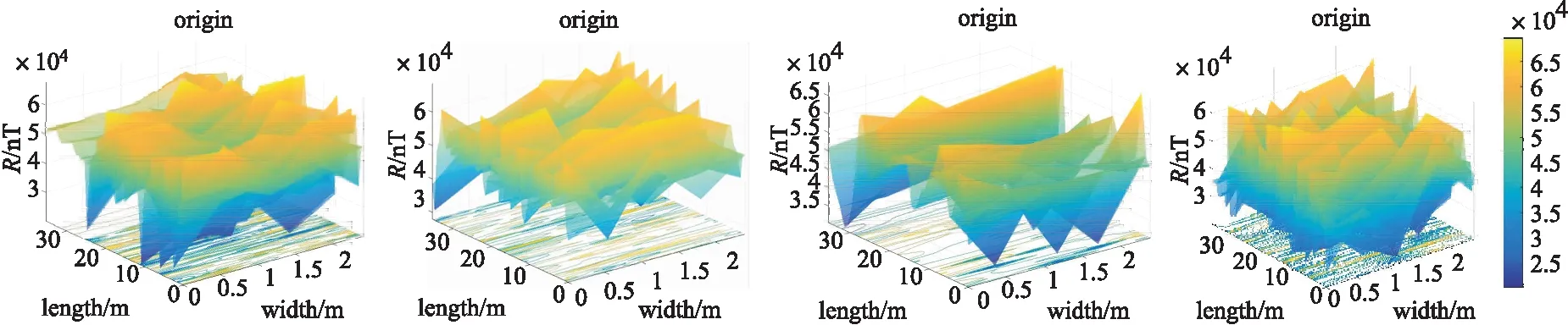
BPT-1 BPT-2 BPT-3 BPT-4图2 研究区地磁基准三维图Fig.2 Three dimensional geomagnetic datum map of the study area

数据地磁特征信息量在数学上描述为匹配区域中的地磁特征量的统计特征，可用标准差SD(Standard Deviation)、信息熵IE(Information Entropy)、粗糙度R(Roughness)、相关系数CC(Correlation Coefficient)等指标描述，见表1.当目标区域内地磁空间分布独特性强、适配性好时，通常地磁数据统计标准差、粗糙度会比较大，而相关系数会比较小.测区内空间点位的磁总场数据，经过粗差剔除后作为巷道地磁基准数据.4个试验样本的地磁数据标准差、信息熵、粗糙度及相关系数的统计特征参数，见表1.

表1 地磁统计特征参数

从表1中，可以看出BPT-1、BPT-2和BPT-4的地磁标准差和地磁信息熵均较大，相关系数较小，说明这3个样本的地磁空间特征丰富，匹配定位适配性强.BPT-3的地磁标准差和地磁信息熵数值较小，相关系数较大，说明该样本地磁空间特征比较贫乏，匹配定位适配性较弱.数字统计特征总体上表明4个试验样本适配性有强有弱，符合测试要求.

2.3 评价指标

去噪效果需要有统一的评价指标，常用的评价指标有信噪比SNR(Signal to Noise Ratio)、峰值信噪比PSNR(Peak Signal to Noise Ratio)和均方根误差RMSE(Root Mean Square Error).

信噪比是衡量信号值噪声水平的物理量，单位为dB，其计算式为：

(9)

峰值信噪比是图像处理中最常用的图像质量评价指标，定义式为：

(10)

均方根误差为：

(11)

式中：Rx为无噪数据，Ry为含噪数据，M、N均为网格点数.

对一幅地磁图像而言，SNR、PSNR和RMSE数值大小可以量化分析去噪质量好坏.PSNR值越大，表明去噪较好，去噪后数据失真较小.而去噪后RMSE的值越小，表明图像数据失真较小.

3 结果与分析

3.1 不同阈值方法小波去噪试验

对图3中4个研究区域原始数据加入服从高斯分布的0.5倍中误差的噪声水平磁数据，作为试验去噪效果依据.试验进行默认阈值wav-R1、自适应阈值wav-R2及极大极小阈值wav-R3的小波去噪处理，图3是研究区的wav-R1、wav-R2的wav-R3小波去噪后的效果图.

从图中可以看出，不同阈值方法小波去噪效果差异明显.其中二维默认阈值wav-R1小波和极大极小阈值wav-R3小波的去噪效果比较差，去噪地磁图总体趋势发生了畸变，未保存住对视觉起主要作用的边沿的变化信息.自适应阈值wav-R2小波去噪效果较好，去噪后图像未发生明显畸变.

对去噪后地磁数据进行去噪特征指标分析，见表2，表中0.5δ为处理数据已知噪声水平，可以作为3种小波阈值去噪的评定依据.从表中可以看出，以BPT-1的研究为例，加入0.5倍中误差噪声后，理论信噪比24.49，均方差为10 074.wav-R1小波去噪SNR值为14.37，和wav-R3去噪后SNR值为15.09相比，明显小于理论信噪比，而均方差分别为 3 935 和 4 302.说明这两种阈值去噪后有过度去噪，出现了地磁信息严重失真.自适应阈值小波去噪信噪比为24.48，峰值信噪比为27.69，均方差为 9 901,与已知噪声理论指标水平最接近.说明二维自适应阈值小波阈值去噪法对这组研究区去噪效果最好.

图3 不同阈值条件下小波去噪效果图Fig.3 Effect diagram of wavelet denoising under different threshold conditions

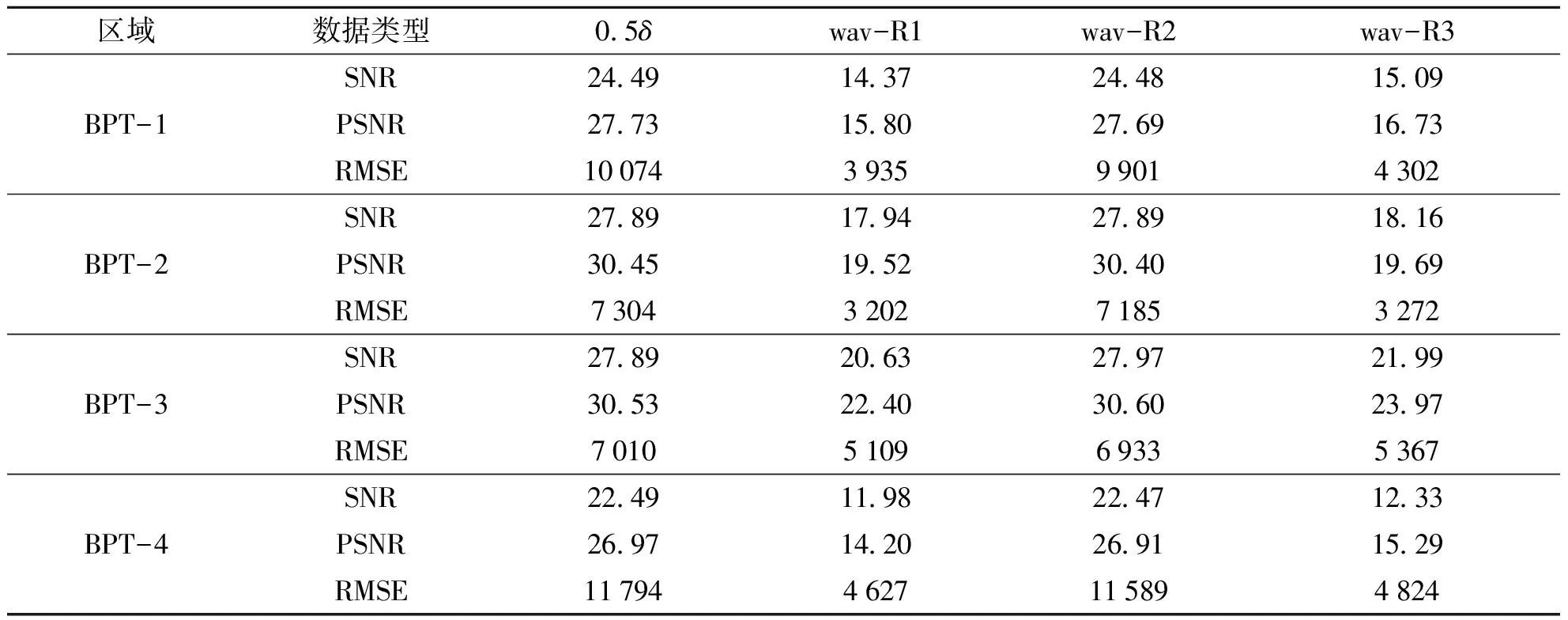
表2 4种方法去噪后的效果指标

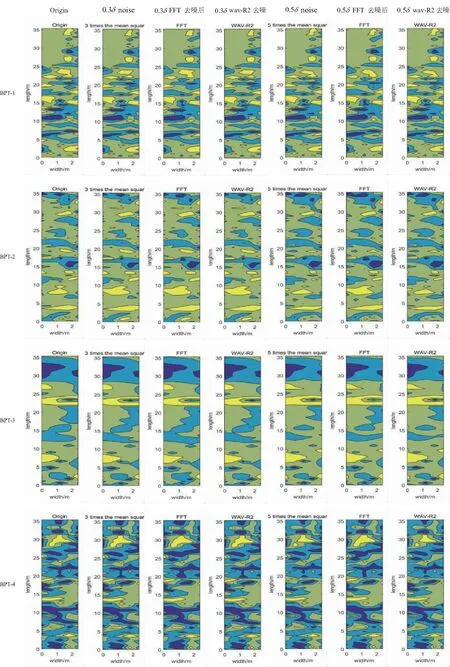
图4 不同去噪方法的去噪前后地磁等值线图Fig.4 Geomagnetic contour map before and after denoising by different denoising methods

3.2 地磁噪声FFT与小波去噪试验

长期以来傅立叶变换是人们信号噪声处理最基本的数学工具，能够处理时频双域全局特性，小波变换去噪在时域或频域同时具有良好局部化性质，在去除噪声方面有明显优越性.试验采用傅立叶FFT变换和自适应阈值wav-R2小波变换，选取4个研究区在0.5倍中误差的噪声水平磁数据，进行噪声去噪试验.图4以0.5倍中误差噪声水平的磁数据为研究区进行傅立叶FFT去噪和自适应阈值wav-R2去噪前后地磁等值线图.从图中可以看出傅立叶FFT变换有明显去噪效果，总体去噪地磁图总体趋势发生了畸变，但是原本磁数据具体细节变化特征部分，去噪后发生一定平滑.如FFT变换去噪后可以看到，BPT-1区域坐标(33，2)附近细节特征消失，BPT-4区域坐标(25，1.5)处信息损失过大，出现严重失真.当然小波变换去噪后，大部分仍然保持局部磁变化特征，但是一些细节隐含噪声并未消除，需要根据去噪后图像细节反复调整阈值选取，来合理去噪.

对去噪后地磁数据进行去噪特征指标分析，见表3，表中0.3δ和0.5δ为处理数据已知噪声水平，可以作为FFT变换和wav-R2小波变换去噪的评定依据.从表中可以看出，FFT变换和wav-R2小波变换都具有一定去噪效果，两种方法去噪的信噪声比与已知理论值非常接近，但是小波去噪效果更为突出，4个测区小波变换后信噪比与理论值非常接近，最大差值仅为0.08，最小的达到了0.01，说明利用小波阈值去噪声总体精度水平较高，稳定性好.

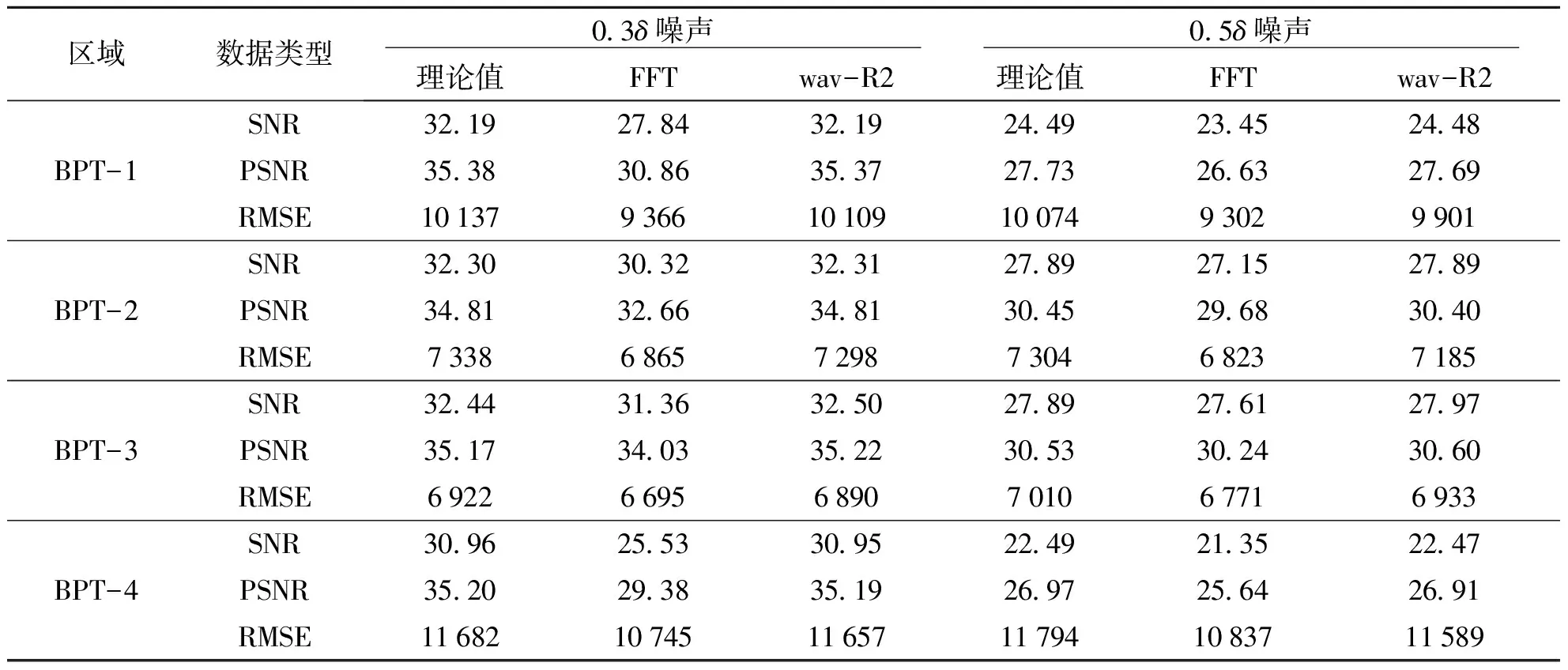
表3 FFT和wav-R2变换去噪后的效果指标

3.3 自适应阈值小波去噪性能测试

选取适配性强的BPT-3研究区和适配性较弱的BPT-4研究区进行小波去噪性能的测试试验，分别对研究区磁数值加入0.1、0.3、0.5、0.7、0.9倍中误差的高斯白噪声后，运用wav-R2小波变换进行去噪处理.试验中误差取为 7 000 nT，即添加的噪声分别为700、 2 100、 3 500、 4 900和 6 300 nT.通过计算去噪评价指标及空间分布统计特征，确认此去噪方法的鲁棒性.图5是不同噪声水平下去噪前后地磁等值线图，从图中可以看出wav-R2变换有明显去噪效果，但是随着噪声水平增强去噪效果下降，同一个地磁图去噪后细节变化特征部分出现明显差异.如BPT-3区域坐标(15，1)至(15，2)附近细节特征，在700和 2 100 nT噪声水平情况下，wav-R2变换去噪后图像与Origin原始图像基本相似，说明低噪声水平去噪效果很好；在噪声水平等于 3 500 nT情况下，wav-R2变换去噪后图像与Origin原始图像细节部分存在差异，但等值线变换方向基本相同；当 4 900 和 6 300 nT噪声水平情况下时，去噪后图像与Origin原始图像存在明显变化，说明wav-R2变换高噪声降噪不突出.在BPT-4区域坐标(30, 1.5)处，去噪后图像与Origin原始图像在0.5、0.7、0.9倍中误差的噪声水平情况下，局部细节信息损失过大，出现一定失真结果.可以得出，小波变换去噪效果和噪声水平大小有一定关系，当噪声水平低于 2 000 nT时，wav-R2变换去噪效果良好，去噪前后能够保持局部磁变化特征.

图5 不同噪声水平下去噪前后地磁等值线图Fig.5 Geomagnetic contour map before and after noise reduction at different noise levels

分别统计了研究区磁数值加入0.1、0.3、0.5、0.7、0.9倍中误差的高斯白噪声的理论信噪比、均方差和实际去噪后计算信噪比、均方差，见表4.表中为0.1、0.3、0.5、0.7、0.9倍中误差的噪声的信噪比理论值为处理数据已知的噪声水平，可以作为小波变换去噪效果的评定依据.从表中可以看出，总体上小波变换去噪后的信噪声比与已知理论值非常接近.BPT-3区域理论与实际信噪比最大差值仅为0.75，最小的达到了0.02，BPT-4区域理论与实际信噪比最大差值仅为0.02，最小的达到了0，说明利用小波阈值去噪声总体精度水平较高，但当噪声在 2 100 nT以内时，均方差差值在100 nT以内，说明对于小噪声去噪效果稳定性更好.

表4 不同噪声水平下自适应阈值小波去噪效果

续表4

图6是两个研究区在0.1、0.3、0.5、0.7、0.9倍中误差的高斯白噪声的理论信噪比、均方差，和实际去噪后计算信噪比、均方差之间差值的柱状图.从图中可以看出总体上小波变换去噪后的信噪声比与已知理论值非常接近，稳定性好，但是在高噪声情况下，均方差和信噪比差值均有增大趋势.

图6 不同噪声水平去噪评价指标差值柱状图Fig.6 Histogram of difference of denoising evaluation indexes at different noise levels

3.4 自适应阈值小波去除噪声匹配有效性检验

为了进一步检验自适应阈值小波去噪对地磁匹配有效性的影响.选取适配性最弱的BPT-3区域和适配性最强的BPT-4区域，进行了试验数据未去噪、FFT去噪和自适应阈值小波去噪后的匹配定位仿真试验.对BPT-3和BPT-4区域20个待匹配地磁序列进行加噪处理，分别加入为700 nT和 3 500 nT随机噪声，进行去噪前后的MSD地磁匹配定位仿真试验.表5列出了去噪前后MSD匹配仿真试验的匹配指标，其中“匹配概率”是指成功匹配序列数与总序列数之比，“匹配误差”是指成功匹配结果的平均误差，“匹配时长”是指地磁序列成功匹配所用时间.

表5 去噪前后MSD匹配结果指标

表5为适配性最弱的BPT-3区域和适配性最强的BPT-4区域不进行去噪、FFT去噪、自适应阈值小波去噪3种状态下匹配结果.适配性最弱的BPT-3区域，当匹配序列中有700 nT的噪声时，未经过去噪处理的磁匹配结果出现了多次误匹配，虚定位次数高，定位精度低.经过FFT、自适应阈值小波去噪后，磁匹配概率得到了明显的提高.其中自适应阈值小波去噪的匹配概率为95%，FFT的匹配概率为75%.当匹配序列中有 3 500 nT的噪声时，不经过处理磁数值匹配定位失败，匹配概率为10，而经过FFT、自适应阈值小波去噪后再进行磁匹配定位的结果，则虚定位现象减少了很多，其中经过自适应阈值小波去噪，匹配概率为90%，而经过FFT去噪后，匹配概率为70%.

适配性最强的BPT-4区域，当匹配序列中有700 nT的噪声时，未经过去噪处理的磁匹配结果出现了多次误匹配，定位精度较低.经过FFT、自适应阈值小波去噪后，磁匹配概率得到了明显的提高.其中自适应阈值小波去噪的匹配概率达到了100%，FFT去噪的匹配概率为95%.当匹配序列中有 3 500 nT的噪声时，未经过去噪处理的磁匹配结果出现了多次误匹配，虚定位次数高，定位精度低.而经过FFT、自适应阈值小波去噪后再进行磁匹配定位的结果，则虚定位现象减少了很多，其中经过自适应阈值小波去噪，匹配概率为95%，而经过FFT去噪后，匹配概率为80%.自适应阈值小波去噪与FFT去噪相对比，自适应阈值小波去噪相对较好.数值上自适应阈值小波去噪的匹配概率更高.

4 结 论

文中针对井下巷道带状区域地磁匹配定位数据噪声扰动影响地磁匹配定位精度问题，选取了傅立叶滤波和小波变换等数学模型进行地磁去除噪声的试验，分析了默认阈值、自适应阈值和极大极小阈值方法的小波去噪灵敏性，验证了小波去噪的可靠性优于FFT变换去噪.通过不同适配性巷道地磁数据去噪前后匹配结果的对比分析，发现自适应阈值wav-R2小波去噪局部去噪精准，能够保持局部磁变化微小特征，具有良好的稳定性.特别是对于 3 500 nT左右的高斯噪声，磁数据wav-R2小波去噪后的MSD匹配试验平均概率达到了90%，说明小波自适应阈值去噪能够有效提高井下巷道带状区域地磁匹配定位的概率和精度，表现较强的鲁棒性.该方法也为面状区域数据降噪提供参考.