学习一致相似度矩阵的图非负矩阵分解

李向利，逯喜燕，范学珍

(1.桂林电子科技大学 数学与计算科学学院， 广西 桂林 541001；2.广西高校数据分析与计算重点实验室， 广西 桂林 541001)

0 引言

近年来，矩阵分解技术在数据表示方面的研究非常活跃。在许多实际的问题中，例如信息检索、模式识别和计算机视觉中，输入数据矩阵的维数非常高，处理这些高维的数据非常困难，因此，人们希望找到2个低维矩阵的乘积来近似高维数据矩阵。一般情况下一个有效的降维方法需要满足以下2个基本要求：第一点是原始数据的维数需要减小；第二点是数据的中隐含的信息和主要的成分能够被有效地挖掘。一些被广泛应用的数据降维方法，例如主成分分析(principal component analysis，PCA)[1]、线性判别分析(linear discriminant analysis ,LDA)[2]、向量量化(vector quantization,VQ)[3]和非负矩阵分解(non-negative matrix factorization，NMF)[4]。其中非负矩阵分解的目标是找到2个非负因子矩阵，它们的乘积能很好地逼近原始矩阵。非负约束导致它们只允许加法组合，而不允许减法组合，从而增强了数据的可解释性。除此之外，非负性约束自然而然地引导出因子矩阵的某种稀疏性的表示，这种稀疏性的表示已经被证明是一种非常有效的特征表达，与完全分布式的或者单一激活成分的表示不同[5]。由于NMF有以上特性，因此在一些实际的聚类任务中取得了非常大的成功。比如NMF在人脸识别[6]和文档聚类[7]方面优于奇异值分解，并且该方法适合学习物体的各个部分。近年来，人们提出了许多NMF变体。Li等[8]提出了局部非负矩阵分解，在基础的非负矩阵分解上施加了局部化约束。该方法不仅可以学习数据的局部结构特征，还可以得到数据的非负表示。非负矩阵分解与许多聚类算法有一定的等价性，如k-means、核k-means以及谱聚类。

虽然NMF有很强的解释性，但是它没有考虑数据的几何结构。几何结构信息是被用来加强NMF方法的一个重要信息。 NMF假设数据点是从欧几里得空间中采样得到的。为了探索数据的几何结构信息，学者们提出了许多流形学习的方法，并且证明了提出的算法能够有效的挖掘数据的潜在结构信息。这些流形学习方法基于局部不变假设，也就是将原始空间中相邻的数据点倾向于具有相似的嵌入。例如局部线性嵌入(locally linear embedding，LLE)[9]首先假设数据在比较小的局部是线性的，即每个数据点都可以由其近邻的几个样本点来线性表示，并且该关系可以在低维空间中得以保持。LLE方法由于在降维时保持样本的局部线性特征，被广泛应用于一些领域，比如图像识别、高维数据可视化等。局部保持投影[10]通过构建空间中样本的远近亲疏关系，并在投影中保持这种关系，尽量保持样本原有的近邻结构。等距映射(ISOMAP)[11]试图使数据在向低维空间映射之后能够保持流形上的测地距离。基于流形上的局部不变假设的启发，Cai[12]等提出了图正则非负矩阵分解(graph non-negative matrix factorization,GNMF)，该方法克服了NMF的局限性。通过构建最邻近图对数据空间的几何信息进行编码并且可以找到一个新的表示空间，在这个空间中，如果2个数据点在图中相连，则彼此足够接近。在GNMF算法中拉普拉斯图一般是基于成对距离构造的。由于成对距离仅依赖于2个数据点之间的关系，因此这种构图的方式对数据的野值和噪声比较敏感。尽管Zeng[13]等提出了超图非负矩阵分解，这种算法的目标函数包含一个超图正则项，虽然超图不只是依赖于两点之间的关系而是考虑多点之间的高阶关系，但这种构图方法也仅依赖于欧氏距离。GNMF中的拉普拉斯图和超图都是基于欧式距离构造的相似度图，所以这种构图方法容易受到野值和噪声的影响。

基于图的非负矩阵分解的启发，为了改善原始数据的野值和噪声对构造相似度矩阵的影响，本文提出学习一致相似度矩阵的图非负矩阵分解(SGNMF)。本文通过自适应的方法首先生成一个相似度矩阵S，通过相似度矩阵产生拉普拉斯图正则项加入非负矩阵分解中来探索数据固有的几何结构，避免了直接使用K-近邻构造拉普拉斯图产生的弊端。

1 相关工作

1.1 非负矩阵分解(NMF)

给出非负数据矩阵X=[x1，x2，…，xn]∈Rm×n，其中X的每一列代表一个样本，X的每一行代表一个特征。NMF的目的是将数据矩阵X分解成2个非负因子矩阵的乘积即X≈UVT，其中U∈Rm×k称为基矩阵和V∈Rn×k称为系数矩阵，k为数据矩阵降维的维数。为了找到2个非负因子矩阵U和V来近似X，一般地，采用欧氏距离的平方作为残差项可以构造如下的最优化问题：

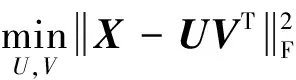
(1)

显然，求解问题(1)是非凸的，得到这个问题的全局最优解是个NP难问题，然而，当固定变量U求解变量V时，该问题是个凸优化问题。当固定变量V求解变量U时，该问题也是个凸优化问题。因此Lee和 Seung[4]提出了如下迭代更新规则：

(2)

(3)

1.2 图正则非负矩阵分解(GNMF)

为了发现数据空间的内在几何结构，Cai等[12]提出了图正则非负矩阵分解(GNMF)。假设X∈Rn×k表示数据矩阵，X的每一列表示一个样本。如果数据点xi和xj在原始的空间中相距比较近，这2点在降维之后的空间中新的数据表示yi和yj也彼此接近。2个数据点之间的相似性通过构造一个权重矩阵W来度量，一般使用的0-1度量定义如下：

(4)

数据点之间的距离一般使用欧氏距离来测量，则有

tr(VTDV)-tr(VTWV)=tr(VTLV)，

(5)

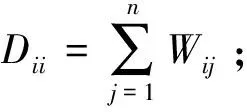
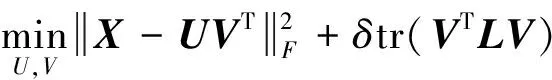
(6)

式中δ表示正则化参数。

该算法的更新迭代公式是

(7)

(8)

1.3 局部学习正则化非负矩阵分解

为了同时研究数据的几何结构和鉴别信息，Gu等[14]提出了局部学习正则非负矩阵分解算法(cocal learning regularized nonnegative matrix factorization,LLRNMF)，将局部学习正则化器集成到原始模型中。局部学习正则化非负矩阵分解算法(LLRNMF)目标函数

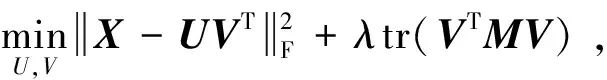
(9)

式中：λ是正则化参数；M=(S-I)T(S-I)，S的元素定义为

(10)

式中N(xi)是xi的领域。同样地，根据交替迭代规则有如下迭代公式：

(11)

其中

(12)

1.4 秩约束非负矩阵分解

基于图正则非负矩阵分解，Shu等[15]提出秩约束非负矩阵分解，对于学习图的拉普拉斯矩阵施加秩约束，使其能够保持连通分量的数量与样本类别数量一致。所提出的框架可以自适应地调整每次迭代中关联矩阵的权重，而不是固定的基于图的正则化。目标函数如下：

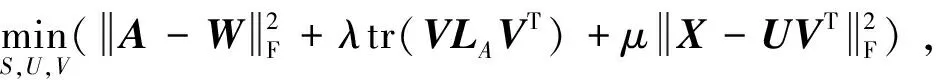
(13)

这个算法U、V的交替迭代公式是

(14)

固定U、V,更新A:

(15)

优化上述问题等价于优下面的问题：

(16)

对于每一行ai和wi有

(17)

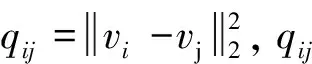
(18)

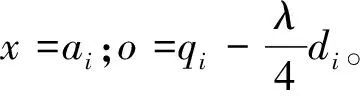
2 基于一致相似度矩阵的图非负矩阵分解(SGNMF)

2.1 学习一致矩阵

给定一个数据集x={x1，x2，…，xn}。数据集x基于m弱基聚类结果C={C1，C2，…，Cm}，每个聚类结果Ci包含k个簇，其中每个聚类结果中k的值可以不同。根据Ci来构造关联矩阵S(i)∈Rn×n如下：

(19)

(20)

为了更好地学习一致矩阵S，定义矩阵S的表达式如下：

(21)

因此，学习一致矩阵S，只需求解S的未知位置的元素即可。

由于S是一致性矩阵，因此希望最小化S和所有连接矩阵之间的不同。一个自然的想法是最小化如下式子：

(22)

(23)

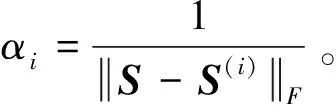
(24)

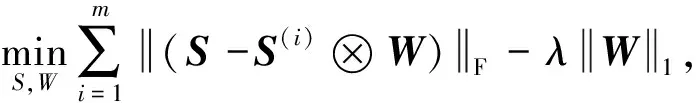
(25)

本文进一步对学习的一致性矩阵S的拉普拉斯矩阵施加秩约束，使其能够保证连通分量的数量与样本类别数量一致提出以下模型：

(26)

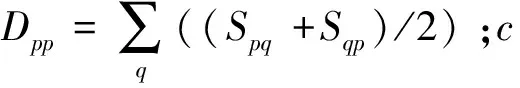
(27)

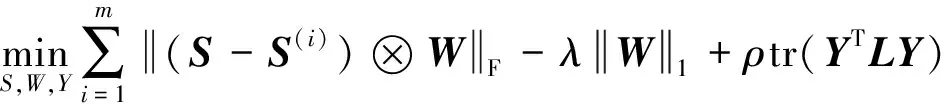
(28)

(29)

模型中的第一项是残差项，其中W是权重矩阵，如果xp和xq越容易配对，那么Wpq的值越大，λ是个平衡参数，第三项是为了保证相似度矩阵S的稀疏性，最后一项是为了保证通过该模型构造的相似度矩阵S恰好有c个连通分量。

2.2 基于一致相似度矩阵的图非负矩阵分解

近年来发展了许多非负矩阵分解的方法，尤其是基于图的方法，在实际应用中取得了令人满意的结果，但是基于图的算法大多都是使用K-近邻来构造图。由于数据中的异常值和错误特征，直接构造的图是不准确的，因此采用上述方法学习一致性相似度矩阵S来构造拉普拉斯矩阵LS，该方法能够更好地学习数据的流形结构，避免了之前直接通过K-近邻来构造图W的弊端。

为了结合数据的几何结构，在学习表达系数矩阵的过程中采用了流形假设[18]，这意味着流形上的近邻xp和xq应该具有类似的表达和vp和vq，也就是说v应该沿着流形表面平滑的变化。对于上述S能够更好地捕获数据局部几何结构信息的表示可以通过最小化以下函数来获得：

(30)

式中Sij表示向量vi和vj之间的相似性。

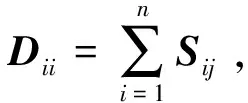
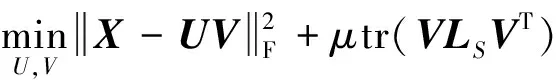
(31)

式中μ是正则化参数，当参数μ=0时，上述式子退化为一般的非负矩阵分解模型。

本文提出的算法SGNMF与NMF算法相比优势在于充分利用了数据的几何结构。SGNMF算法与GNMF算法相比优点是避免了数据样本中的噪声和异常值对构造相似度矩阵的影响。SGNMF算法是通过自适应来学习相似度矩阵，然后通过相似度矩阵构造拉普拉斯图，最后将拉普拉斯图正则化项加入到非负矩阵分解的模型框架中。虽然秩约束非负矩阵分解是通过自适应的方法来学习相似度矩阵，但是该方法相似度矩阵初始值仍然是使用基于欧氏距离学习的K-近邻图。提出的方法中相似度矩阵的初始值设置避免了直接使用K-近邻图，具体操作在试验部分介绍。SGNMF方法与秩约束非负矩阵分解方法相比，本文的方法能够更好的学习数据的几何结构和潜在信息。

2.3 优化算法

首先求解模型(29)，由于该模型涉及4个变量，因此采用固定其他变量来求解另一个变量的方法迭代求解该模型。

首先优化变量W，将式(29)去掉与W无关的项得到如下式子：

(32)

式中，A(i)=S-S(i)。(31)式能够等价于求解n×n个独立子问题，其中一个子问题如下：

(33)

上述式(33)对Wpq求偏导可得

(34)

又由于Bpq≥0，λ≥0，因此最终的Wpq的求解结果为

(35)

其次优化变量S，当式(29)其他变量固定时可得如下式子：

(36)

式中yp和yq分别是Y的第p和q行向量。

本文首先定义一个函数如下：

(37)

(38)

式(38)能够进一步简化为

(39)

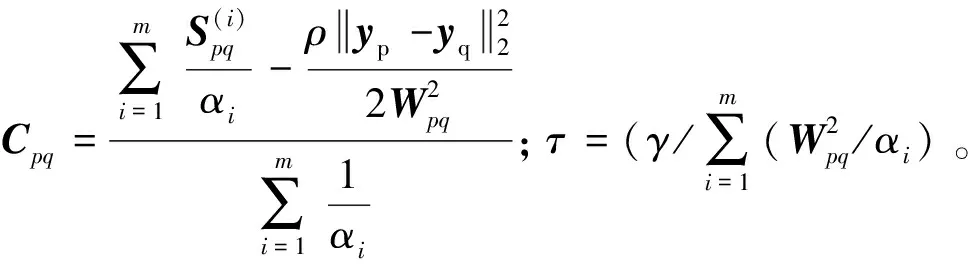
求得式(39)的闭式解为

(40)

对变量Y进行优化时，则有

(41)

根据参考文献[16]，Y的解由拉普拉斯矩阵L的c个特征向量对应c个最小特征值构成。

最后对α进行更新，令

(42)

有

(43)

根据柯西施瓦茨不等式，则有

(44)

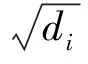
(45)

上述模型(31)是关于变量U和V的，如果同时求解U和V该问题是很难求解的。如果固定一个变量求解另一个变量，该问题变成了一个凸优化问题非常容易求解。交替求解U和V。

由于U≥0，V≥0，引入拉格朗日乘子γ∈Rd×m，η∈Rm×n，因此，拉格朗日函数为

(46)

γ=-2XVT+2UVVT，
η=-2UTX+2UTUV+2μVL。

(47)

使用KKT条件γijUij=0和ηijVij=0，可得到

(-XVT+UVVT)ijUij=0，

(-UTX+UTUV+μVLS)ijVij=0，

(48)

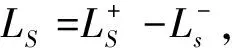
(-XVT+UVVT)ijUij=0，

(49)

得到最终的迭代公式为

(50)

3 数值试验

本节将进行图像数据试验来评估所提出算法的性能。将本文提出的算法在4个图像数据集上进行了试验分别是USPS数据集、yale数据集和faces数据集和ORLdata数据集，该算法并与k-means[19]、NMF[4]、GNMF[12]、RCNMF_l2[15]、RNMF[20]进行比较。为了能够更好地验证算法的性能，首先设置每个数据集的聚类数目和原始的类别数一致，对每个数据集重复10次试验，并计算平均聚类性能。对于k-means该法可以直接得到标签信息，而对于NMF、 GNMF、RCNMF_l2、SGNMF、RNMF首先学习低维表示，然后得到的低维表示再利用k-means得到标签信息。为了避免随机性结果的影响每个试验重复20次取均值。SGNMF算法中相似度矩阵的初始值的设置是首先使用k-means对原始数据矩阵进行聚类，重复试验5次得出聚类结果，相似度矩阵的初始值是取这5次聚类结果产生的关联矩阵的均值。

3.1 评价准则

对于试验效果使用准确率(accuracy，ACC)和互信息(mutual information，MI)作为评价指标，ACC和MI的计算方法参考文献[12]。

3.2 参数选择

本文提出的算法只有一个平衡参数μ，下面将从试验中分析参数μ对聚类结果的影响并选择最优参数值。SGNMF算法在USPS数据集、ORLdata数据集和yale数据集和faces数据集上进行试验。在上述试验中取值为0.01、0.1、0.5、1、2、5、10、20、50、100。对于每个值SGNMF算法在4个数据集上进行10次试验，试验结果为10次试验的均值。具体试验结果如图1和图2所示。从图1中可以看出：在ORLdata数据集和USPS上当μ=0.01时，ACC可以取到最优值，它们的最优值分别为0.696 3和0.652 3；当μ=50时，在数据集faces上ACC指标达到最优值，最优值为0.945 0；当μ=5时，在数据集yale上ACC指标取到最优值，最优值为0.515 0。从图2中可以看出：在ORLdata数据集和USPS数据集以及yale数据集上当μ=0.01时，NMI同时可以取到最优值，它们的最优值分别为0.858 9和0.563 2和0.515 0；当μ=20时，在数据集yale上ACC指标达到最优值，最优值为0.515 0。

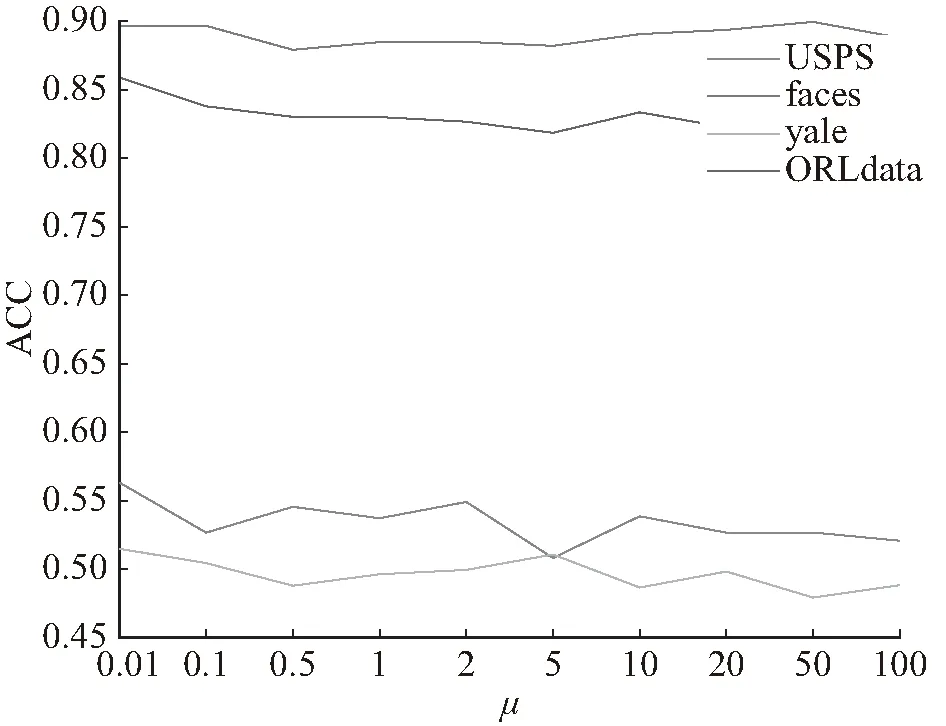
图1 SGNMF相对于参数μ在4个数据集上的聚类精度变化曲线Fig.1 Vaiation curve of clustering accuracy of SGNMF relative to paramete μ on four data sets

图2 SGNMF相对于参数μ在4个数据集上的聚类精度变化曲线Fig.2 Vaiation curve of mutual information of SGNMF relative to paramete μ on four data sets

3.3 ORLdata数据集试验结果

ORLdata数据集从40个人中收集了400张人脸图像，每人有10个灰度图像。这些图像在不同的光照条件下拍摄的，具有不同的表情和戴或不戴眼镜。

从表1和表2可以看出在ORLdata数据集中，SGNMF的性能优于GNMF，平均ACC和NMI分别比GNMF高14%和10%，SGNMF在ACC和NMI分别比RCNMF_l2高大约54%和59%，这是由于SGNMF避免了直接利用原始数据构造拉普拉斯图是存在噪声和野值的影响。SGNMF在ACC和NMI分别比k-means高大约6%和3%，SGNMF在ACC和NMI分别比NMF高大约46%和40%，说明SGNMF充分利用了数据的几何结构信息。SGNMF在ACC和NMI 2个衡量指标上比RNMF分别高出11%和9%。

3.4 USPS数据集试验结果

USPS数据集包含从‘0’到‘9’的10类手写数字。整个数据集库有9 298张灰度图像。表1和表2第二列分别显示了在数据集USPS上的结果，可以看出，在USPS数据集上SGNMF与NMF相比，在ACC和NMI这2个度量上的优势分别是13%和11%，并且与GNMF相比在ACC和NMI指标上的优势分别是17%和4%。SGNMF在NMI和ACC衡量指标上比RCNMF_12分别高出53%和55%。在USPS数据集上SGNMF与HNMF相比，在NMI和ACC度量指标上优势分别为9%和2%。SGNMF在NMI和ACC衡量指标上比k-means分别高出3%和1%。加入一致学习相似度矩阵的拉普拉斯正则项后使得SGNMF性能有所提高。

3.5 yale人脸数据集试验结果

yale是人脸图片数据集，包含40个人不同表情光照下的图片共400张，每个人10张图片。本次试验，每张图像处理成分辨率为32像素×32像素。表1和表2第四列显示了在数据集yale上的结果，表明SGNMF方法比所有比较方法都取得了最好的结果，在指标ACC和NMI上分别优于GNMF 21%和14%。SGNMF在yale数据集上ACC和NMI指标比RCNMF_l2分别高出31%和29%，而比NMF高出19%和15%。从yale数据集上的聚类结果可以看出，SGNMF与k-mean相比，在ACC和NMI指标上的优势分别为11%和5%。SGNMF与RNMF相比在ACC和NMI指标上的优势分别为10%和3%。yale数据集的图像质量与其它数据集相比是最差的，数据集中的噪声和野值会影响构图的质量，在这个数据集上流形学习方法不如在其它数据集上表现的好。实际上，yale数据集上平均聚类精度是最低的与其它数据集相比，但是本文提出的方法仍然可以在该数据集上表现出良好的性能。

3.6 faces数据集试验结果

faces是人脸数据集包含38 416个特征，100个样本并且包含10个类别数。为了试验方便，随机选取4个类别进行试验，聚类结果列在表1和表2的第三列。从试验结果中可以看出，本文提出的方法在faces数据集上表现均优于GNMF，说明图像中的噪声对数据集的构图是有影响的，SGNMF方法可以有效提高构图的质量。SGNMF与NMF相比，在ACC和NMI上的优势分别是8%和6%，SGNMF在ACC和NMI上比RCNMF_12分别高出11%和12%。SGNMF在faces数据集上ACC和NMI比k-means分别高出2%和4%。SGNMF在faces数据集上的2个度量指标ACC和NMI比RNMF分别高出2%和2%。从试验结果分析可知，本文的算法在该数据集中也明显优于其它的算法。

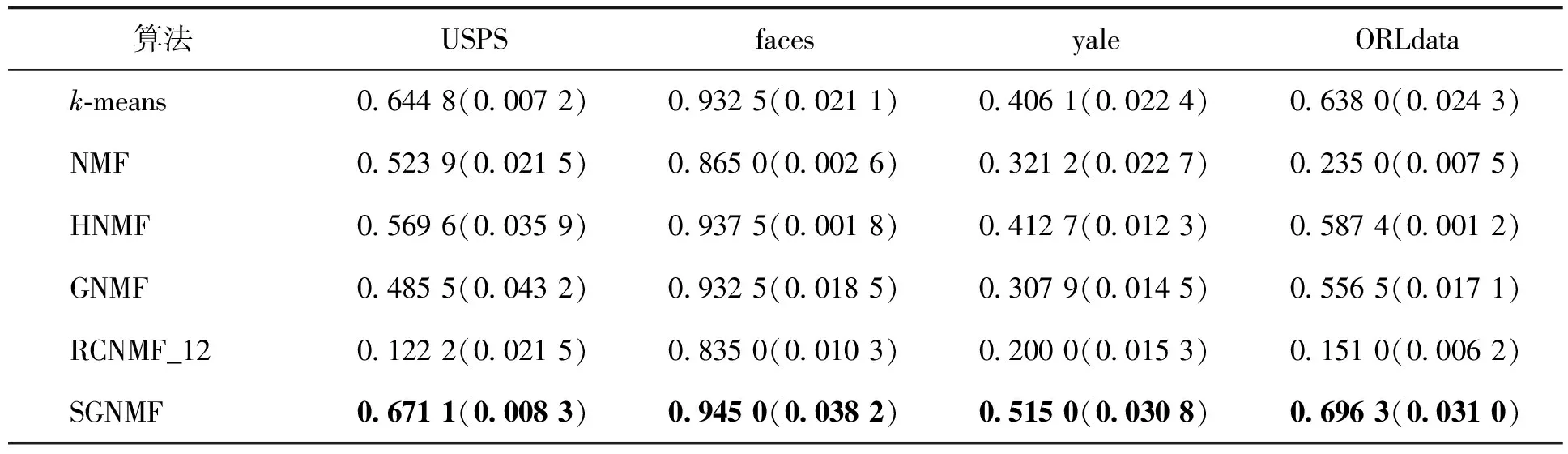
表1 数据ACC试验结果Tab.1 Experimental results of ACC on dataset

表2 数据NMI试验结果Tab.2 Experimental results of NMI on dataset

4 结束语

本文提出了一个基于学习一致性相似图的非负矩阵分解算法。该算法首先自适应学习比较稳健的一致性相似度矩阵，然后通过一致性相似度矩阵来构造拉普拉斯图，最后将拉普拉斯正则项加入到非负矩阵分解模型中。本文学习相似度矩阵的方法能够更好地挖掘数据的几何结构信息，提高了聚类效果，实验证明了提出的算法相比现有的一些算法性能是有所提升的。该算法的缺点是学习相似度矩阵的速度相对来说较慢，希望以后能够找到更好的学习相似度矩阵的方法以提高求解速度。