NHPP类开源软件可靠性增长模型的极大似然估计
2022-05-07陈静杨剑锋王喜宾李华
陈静,杨剑锋,王喜宾,李华
(1.贵州中医药大学 信息工程学院, 贵州 贵阳 550025;2.贵州理工学院 大数据学院, 贵州 贵阳 550003;3.贵州师范大学 大数据与计算机科学学院, 贵州 贵阳 550025)
0 引言
自20世纪90年代以来,开源软件由于其开发模式的转变,得到了快速发展,例如Android、大数据分析系列平台(Hadoop、MapReduce、HDFS、Hbase、NoSQL、Mahout)、Linux、Apache Server、Firefox、MySQL等开源产品取得了很大成功。开放源代码提供了一种自由的、快捷的、稳定的软件产品开发模式,具有强大的网上社区技术支持。开源项目在很大程度上依赖于志愿者的参与和时间投入,这些会由于个人因素而极易改变。开源软件开发过程中有不少工具来辅助提高开源软件的质量,其中Bugzilla缺陷跟踪管理系统是当前开源软件组织使用最多的一个错误报告系统,各大开源软件开发团队均利用该工具进行缺陷管理。相比传统的闭源商业软件,人们更容易从开源项目中免费获取实时在线故障数据,以便进行可靠性理论分析与研究。
非齐次泊松过程(non-homogeneous Poisson process,NHPP)类开源软件可靠性增长模型[1-5]常常用于描述软件的失效过程。软件可靠性不但与软件存在的缺陷和(或)差错有关,而且与系统输入和系统使用有关。影响传统闭源软件可靠性增长的因素较多,比如软件复杂程度、需求定义错误、测试效率、测试强度、故障检测率、故障暴露率、故障排错与纠正率、故障引入、变点、用户行为、环境因子等。与传统闭源软件的开发过程相比,开源软件有许多独特之处,软件工程师根据软件的可靠性变化和开发情况决定新版本的发布时间和维护旧版本的人数。如今,对开源软件可靠性建模主要体现在NHPP类可靠性模型[6-10]、随机微分方程类可靠性模型[11-13]以及机器学习类可靠性模型[14-16]等方面的研究。极大似然估计方法常用于估计软件可靠性模型中的未知参数,当前已有一些学者研究了软件可靠性模型中极大似然估计的性质[17-18]。
1 NHPP类开源软件可靠性增长模型
为了建立NHPP类软件可靠性增长模型,需要做如下基本假设:①软件失效的检测过程可以用NHPP来描述;②系统剩余的缺陷引起软件的当前失效;③单位时间内发现的故障数与测试覆盖率成正比;④排错过程中不会引入新的缺陷。
记N(t)为(0,t]时间段内检测出的累计故障数,[N(t),t≥0]是一个独立的增量过程;m(t)为(0,t]时间段累计故障数的期望值,m(t)=E[N(t)];λ(t)为失效强度函数,表示单位时间内发现的故障数。由上述假设可得
(1)
式中:a为软件中固有的错误数;b(t)为故障发现率函数,表示在时刻t软件中潜伏的每个故障被检测到的概率。解微分方程得
(2)
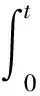
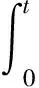
(3)
进一步可得软件系统的失效强度函数为
(4)
根据模型的基本假设和非齐次泊松过程的性质,可得软件系统的可靠性函数为

(5)
另外,软件系统在(t,t+Δt)时间区间里不发生失效的概率为
R(Δt|t)=exp{-[m(t+Δt)-m(t)]}。
(6)
根据公式(3),对故障检测率函数b(t)取不同形式时,可以得到不同的NHPP可靠性模型。本文分以下几种情况进行讨论:
①当b(t)=b时,得到GO (Goel-Okumoto)模型,其均值函数和失效强度函数分别为
m(t)=a(1-e-bt),
(7)
λ(t)=abe-bt。
(8)

m(t)=a[1-(1+bt)e-bt],
(9)
λ(t)=abt2e-bt。
(10)
③当b(t)=bctc-1,得到GGO (generalized goel)模型,其均值函数和失效强度函数分别为
m(t)=a[1-exp(-btc)],
(11)
λ(t)=abctc-1e-btc。
(12)
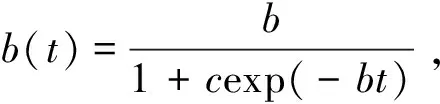
(13)
(14)
⑤为了改进GO模型中的缺陷,不完全排错的NHPP类模型由Ohba提出,其均值函数和失效强度函数分别为
(15)
λ(t)=abe-b(1-β)t。
(16)
表1给出了常见的NHPP类软件可靠性增长模型,并给出了其均值函数、故障检测率函数和失效强度函数。

表1 常见的NHPP类软件可靠性增长模型Tab.1 Selected NHPP-based software reliability growth model
2 可靠性增长模型参数的极大似然估计
针对软件测试过程中常见的不分组失效数据和分组失效数据,本文将分别给出模型参数的极大似然估计过程。
2.1 NHPP类开源软件可靠性增长模型的极大似然估计
2.1.1 分组数据下的似然函数
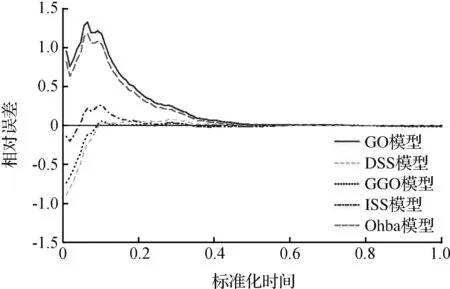
记(tk,mk)(k=1,2,…,n;0 L(θ)=P{N(t1)=m1,N(t2)=m2,…,N(tn)=mn}= (17) 式中θ为待估计的参数向量。进一步可得对数似然函数为 (18) 2.1.2 不分组数据下的似然函数 设观测的失效时间序列为{t1,t2,…,tk,…,tn},则模型的似然函数(即序列t的联合概率密度函数)为 (19) 进一步可以得到对数似然函数为 (20) 2.2.1 分组数据下GO模型的极大似然函数 根据表1和公式(19),可以得到分组数据下GO模型的似然函数为 (21) 进一步可以得到对数似然函数为 (22) 分别对参数求偏导数,可以得到分组数据下GO模型的似然方程组: (23) 参数的极大似然估计(maximum likelihood estimation,MLE)可以通过数值算法求解上述似然方程组而得到。 2.2.2 不分组数据下GO模型的极大似然估计 根据表1和公式(19),可以得到不分组数据下GO模型的似然函数为 (24) 进一步可以得到对数似然函数为 (25) 分别对参数求偏导数,可以得到不分组数据GO模型的似然方程组 (26) 模型参数的MLE可以通过数值算法求解上述似然方程组而得到。 2.3.1 分组数据下DSS模型的极大似然估计 根据表1和公式(17),可以得到分组数据下DSS模型的似然函数为 (27) 进一步可以得到对数似然函数为 (28) 分别对参数求偏导数,可以得到分组数据下DSS模型的似然方程组 (29) 模型参数的MLE可以通过数值算法求解上述似然方程组而得到。 2.3.2 不分组数据下DSS模型的极大似然估计 根据表1和公式(19),可以得到不分组数据下DSS模型的似然函数为 (30) 进一步可以得到对数似然函数为 (31) 分别对参数求偏导数,可以得到不分组数据下DSS模型的似然方程组 (32) 模型参数的MLE可以通过数值算法求解上述似然方程组而得到。 2.4.1 分组数据下GGO模型的极大似然估计 根据表1和公式(17),可以得到分组数据下GGO模型的似然函数为 (33) 进一步可以得到对数似然函数为 (34) 分别对参数求偏导数,可以得到分组数据下GGO模型的似然方程组 (35) 模型参数的MLE可以通过数值算法求解上述似然方程组而得到。 2.4.2 不分组数据下GGO模型的极大似然估计 根据表1和公式(19),可以得到不分组数据下GGO模型的似然函数为 (36) 进一步可以得到对数似然函数为 (37) 分别对参数求偏导数,可以得到不分组数据下GGO模型的似然方程组 (38) 模型参数的MLE可以通过数值算法求解上述似然方程组而得到。 2.5.1 分组数据ISS模型的极大似然估计 根据表1和公式(17),可以得到分组数据下ISS模型的似然函数为 (39) 进一步可以得到对数似然函数为 logL(a,b,c)= 分别对参数求偏导数,可以得到分组数据下ISS模型的似然方程组 (41) 模型参数的MLE可以通过数值算法求解上述似然方程组而得到。 2.5.2 不分组数据ISS模型的极大似然估计 根据表1和公式(19),可以得到不分组数据下ISS模型的似然函数为 (42) 进一步可以得到对数似然函数为 (43) 分别对参数求偏导数,可以得到不分组数据下ISS模型的似然方程组 (44) 模型参数的MLE可以通过数值算法求解上述似然方程组而得到。 2.6.1 分组数据Ohba模型的极大似然估计 根据表1和公式(17),可以得到分组数据下Ohba模型的似然函数为 (45) 进一步可以得到对数似然函数为 (46) 分别对参数求偏导数,可以得到分组数据下Ohba模型的似然方程组 (47) 2.6.2 不分组数据Ohba模型的极大似然估计 根据表1和公式(19),可以得到不分组数据下Ohba模型的似然函数为 (48) 进一步可以得到对数似然函数为 (49) 分别对参数求偏导数,可以得到不分组数据下Ohba模型的似然方程组 (50) 本节在软件可靠性工程中的分组失效数据和不分组失效数据2种情形下,给出了NHPP类开源软件可靠性增长模型参数的极大似然估计的一般形式,尤其研究了GO模型、DSS模型、GGO模型、ISS模型Ohba模型的极大似然估计问题,对可靠性建模研究具有重大的理论和现实研究意义。 Tomcat服务器软件是Apache 软件基金会的一个重要开源项目,深受并发访问用户不多和中小型系统的研发者欢迎,是一个免费的轻量级Web 应用服务器。由于Tomcat 服务器存在相关缺陷,例如,攻击者可以利用Tomcat文件包含漏洞,读取webapp 目录下的任意文件,使得研究Tomcat 服务器软件的可靠性尤为重要,为进一步提高开源系统的质量具有重要的现实意义。本文研究的故障数据来源于Tomcat 5的用户缺陷跟踪系统https://bz.apache.org/bugzilla/。从缺陷跟踪系统中提取了从2003年1月至2011年12月共计108个月(9 a)的失效数据,开源软件Tomcat 5失效数据见表2。本文将失效数据分为2组:第一组数据(第1—84个月)为训练集,用于估计模型中的参数,并判断模型的拟合效果;第二组数据(第85—108个月)为测试集,用于判断可靠性模型的预测效果。 表2 开源软件Tomcat 5失效数据Tab.2 Failure data of open source software for Tomcat 5 均方误差(mean square error,MSE)已经广泛应用于模型的拟合优度检验中,其值用字母M表示,M越小代表模型越好。MSE定义为 (51) AIC信息准则(akaike information criterion,AIC)是衡量统计模型拟合优良性的一种标准,其值用字母A表示,A越小代表模型越好。AIC定义为 A=2K-2logL, (52) 式中:K是参数的数量;L是极大似然值。若模型的误差服从独立正态分布,则AIC可以定义为 (53) 式中:m为样本观测容量;R为残差平方和。为了考虑参数个数对模型拟合度的影响,对MSE进行调整,得到如下调整的MSE: (54) 相对误差(relative error,RE)可以是一种常见的模型预测有效性的判断标准,其值用字母E表示,E越接近零表示模型预测更准确。RE定义为 (55) 式中:m(tq)为估计值;mq为实际观测值。 本文用于模型性能对比分析的可靠性模型(表1),表3给出了各模型的参数估计结果和比较结果。可以看出:GO模型的M(13 020.1 168)、A(799.8 371)和Madj(13 337.6 806)3个拟合度评估指标比其他4个可靠性模型的值要大;另一方面,GGO模型的M(154.338 5)、A(429.2 885)和Madj(160.054 7)3个拟合度评估指标比其他4个可靠性模型的值都要小。从上面分析可以看出,对于本文的失效数据,GGO模型的拟合效果最好,而GO模型的拟合效果最差。各模型的失效拟合效果如图1所示。从图中可以看出,DSS模型、GGO模型和ISS模型的累计故障数拟合效果较好,而GO模型和Ohba模型的拟合效果较差。各模型的失效预测效果如图2所示。可以看出,标准化时间60%以后,RE值都接近0,说明所有的模型都具有较好的预测效果。 表3 参数的极大似然估计和模型比较结果Tab.3 Results of MLE for parameters and model comparison 图2 各模型的失效预测效果Fig.2 Failure predication effect for all selected models 本文在分组数据和不分组数据下,给出了NHPP 类开源软件可靠性增长模型极大似然估计的一般形式;分别对GO模型、DSS模型、GGO模型、ISS模型和Ohba模型进行了讨论,给出了模型的似然函数和似然方程;最后,提取了开源软件Apache Tomcat 5 的失效数据(2003年1月至2011年12月共计108个月),对模型进行性能对比分析,结果显示GGO模型具有较好的拟合与预测效果,而GO模型的拟合效果最差。2.2 GO模型的极大似然估计

2.3 DSS模型的极大似然估计

2.4 GGO模型的极大似然估计
2.5 ISS模型的极大似然估计
2.6 Ohba模型的极大似然估计
3 案例分析
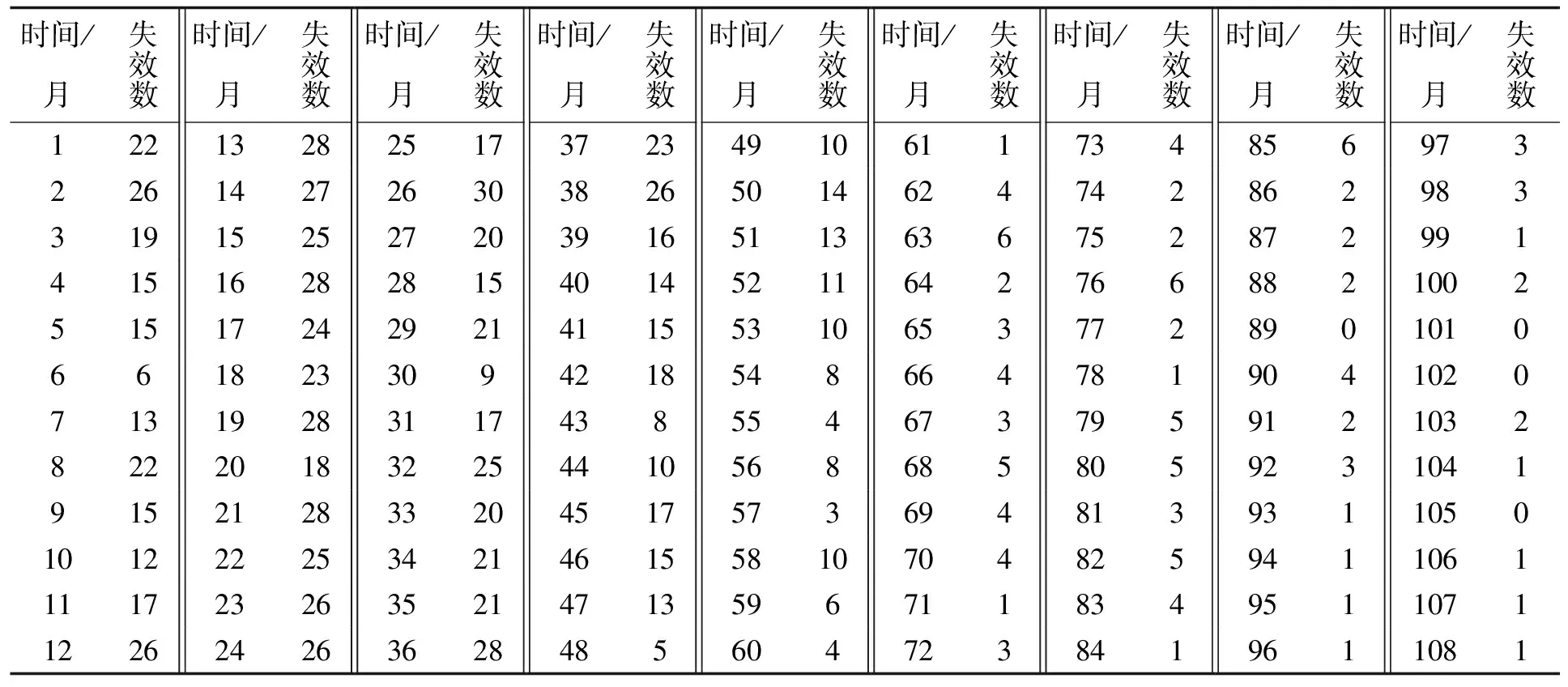
3.1 失效数据
3.2 模型评估准则
3.3 模型性能对比分析

4 结论
