MIMO信道相关性简化模型

王学英，周杰*，2，吴苏洁，吕智康

(1.南京信息工程大学 电子与信息工程学院，江苏 南京 210044；2.日本国立新泻大学 电气电子工学部，日本 新泻 950-2181)

0 引言

在无线通信的发展过程中，研究初期技术的不成熟致使频谱资源的不当使用与浪费，造成了现如今频谱资源的极度匮乏，大规模多输入多输出(multiple-input multiple-output，Massive MIMO)系统以其不额外消耗频谱资源的基础上提高蜂窝小区系统容量的优势，在最新的第五代移动通信系统(5G)中得到了广泛应用。Massive MIMO的提出至今已有十年多，它是针对多用户MIMO技术在配备大量天线的小区和TDD基站中的极端情况而提出的，在现有设备基础上，可以大幅度提高频谱效率。为了充分利用Massive MIMO系统，需不断对其进行性能研究完善。

文献[1-2]中提出一种大角度角域扩展的均匀入射信号到达角(angle of arrival，AoA)近似闭式表达式，研究了天线单元间的相互耦合效应对均匀AoA相关性的影响，但只考虑了AoA均匀分布或类似均匀分布的情况，未就实际传输环境中的AoA进行拟合验证。文献[3-5]研究了独立同分布天线单元下空域相关性对信道容量的影响，但实际环境中的天线阵元之间并不是独立分布的，受天线间距的影响，需要考虑天线阵元间相互耦合的情况。文献[6-7]表明相关性对于系统的分集增益及信道容量都有一定的影响，互耦效应可以增加信道容量。

上述研究中，仅考虑影响因素中的若干项，不够全面，因而本文针对收发侧天线阵列相互耦合的Massive MIMO信道提出了一种简化计算模型，综合考虑角域扩展、互耦效应等影响，详细讨论并推导出在大角度扩展下入射信号到达角功率谱的角域采样简化表达式，通过仿真得出不同条件下的信道容量结果及绝对误差等，验证该模型的有效性及准确性。

1 信道模型

1.1 Massive MIMO系统

Massive MIMO是在MIMO系统的基础上发展的。区别于传统的MIMO系统，Massive MIMO系统在收发两侧皆配备至少上百个天线单元，并采用波束合成技术，通过空间隔离使得同一频率下可以同时传输多条信号，实现空间复用，极大地提高了蜂窝小区容量及频谱资源利用率。图1所示为Nt×Nr的MIMO系统模型，该系统同时具有Nt个发射天线单元和Nr个接收天线单元，一般地假设接收天线单元数量多于或等于发射天线数量，即Nr≥Nt，如此一来，天线间的干扰更小，具有高鲁棒性。对于传统的MIMO信道，通常假设天线各单元间是独立同分布的，此时收发端之间的信道传输矩阵H可表示为[8-9]

(1)

式中，Rr为Nr×Nr的接收端相关性矩阵，Rt为Nt×Nt的接收端相关性矩阵；Hw为Nr×Nt的独立同分布的高斯信道矩阵，它由定向频率下的频率非选择性瑞利衰落信道的信道冲激响应决定。为简化分析，本研究考虑二维分布场景，假设通信系统收发两端的天线单元排列为ULA，天线单元的转向矢量rnc(φ,θ)只考虑水平面角φ的影响，将仰角设置为θ=90°，此时rnc(φ)=[1,ej2πd/λ·cosφ,…,ej2πd(M-1)/λ·cosφ]T，其中M为天线单元总数，[·]T表示向量或矩阵的转置。通常假设发送端相关性矩阵为单位矩阵，只考虑接收端相关性矩阵的影响，即Rt=INt，此信道中系统容量的统计均值可表示为[10-12]

(2)

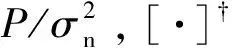
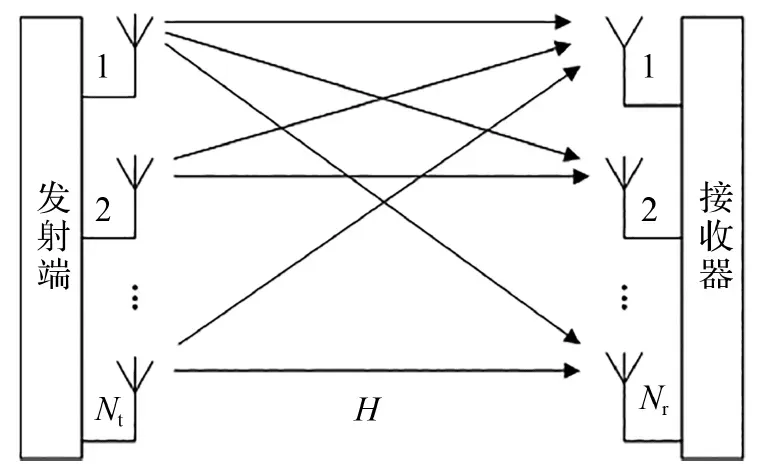
图1 Massive MIMO系统模型Fig.1 Massive MIMO system model

1.2 互耦效应

天线单元之间距离过近时，天线单元之间会产生互耦效应，互耦效应一般可以通过耦合矩阵来体现，假设收发端天线皆为半波偶极子天线，根据文献[13]可得天线耦合矩阵可以表示为

CR=(ZA+ZL)(Z+ZLI)-1,

(3)

其中:ZA为阵元在自由空间里的输入阻抗，在本研究中取值为ZA=73+j42.5 Ω;ZL为匹配负载;Z为天线阵元间的互阻抗矩阵，矩阵内各元素可表示为[14]

(4)

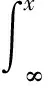
2 相关性简化模型

2.1 无互耦时的简化模型

本研究假设Massive MIMO通信系统中的AoA平面角φ的概率密度函数为p(φ)，该函数服从于均匀分布、高斯分布以及拉普拉斯分布，AoA功率谱概率密度函数为f(φ)，假设天线单元间相互独立时，角域中任意AoA功率谱的空间衰落相关性是可表示为[15]

(5)

式中φ0为AoA中心角均值，通过式(5)可以计算出任意AoA功率谱的空间衰落相关性，但采用数值积分的形式计算相关性，计算时间比较长，对CPU的要求也比较高，基于此本文提出了一种基于角度域采样脉冲的简化计算模型，利用有限采样脉冲的加权系数叠加，得到任意角域功率谱分布的空域相关性计算表达式。假设天线阵元间不存在互耦效应时，该表达式可写为

(6)

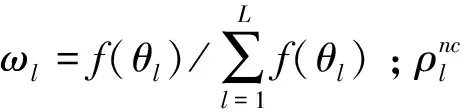
(7)

(8)

(9)

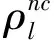
(10)

(11)

(12)

式(10)～(12)中，m、n分别为第m、n个天线单元，将式(10)～(12)代入式(6)可得AoA功率谱的相关性表达式，后面的表达式中将选取第1、2个天线单元，即m=1，n=2,此时AoA功率谱的相关性表达式可写为

(13)

(14)

(15)

式(13)～(15)中，U、G及L分别为归一化系数[16]。式(13)～(15)即为本文提出的空域相关性简化模型在无互耦下的闭式表达式。

2.2 互耦效应下的简化模型

在实际的传播环境中，还需考虑天线单元间相互耦合的情况，以第1、2个天线单元为例，考虑互耦效应时，角域中任意AoA功率谱的空间衰落相关性是可表示为[17]

(16)

式中:P1P2为天线平均接收功率；r(φ)为互耦效应下的天线转置矢量，是通过耦合矩阵点乘无耦合时的接收信号处的天线矢量[17]修正后得到的列向量。互耦效应下AoA的空间相关性可表示为[18]

(17)

(18)

(19)

(20)

式(18)～(20)中，Re(·)与Im(·)分别为矩阵的实部与虚部，(·)*代表矩阵的共轭转置，c=b/a，此时式(6)可以修改为

(21)

将式(18)～(20)代入式(21)即可得到本文提出的空域相关性简化模型在互耦效应下的闭式表达式。

3 仿真分析

3.1 非对称几何模型

本文首先以微蜂窝和微微蜂窝移动系统中的全向小区场景下的非对称几何模型[19]为例，其中散射体分布在半径为R的饼状切割区域,研究适于该模型的指数分布来验证、拟合及分析简化模型，该分布可表示为

f(φ)=ae-ar，

(22)

式中，r∈[0,R]，a=1/R为非对称几何模型中移动台(MS)位置参数。

图2所示为非对称几何模型的边缘概率密度函数。图2表明非对称模型的概率密度函数也是非对称的，本研究仅使用其中标位‘used’的曲线，设置的仿真参数如下：m=1，n=2，R=100，天线间隔d=(0～5)λ，角度扩展为4°～16°，采样脉冲数目与角度扩展的大小成反比。

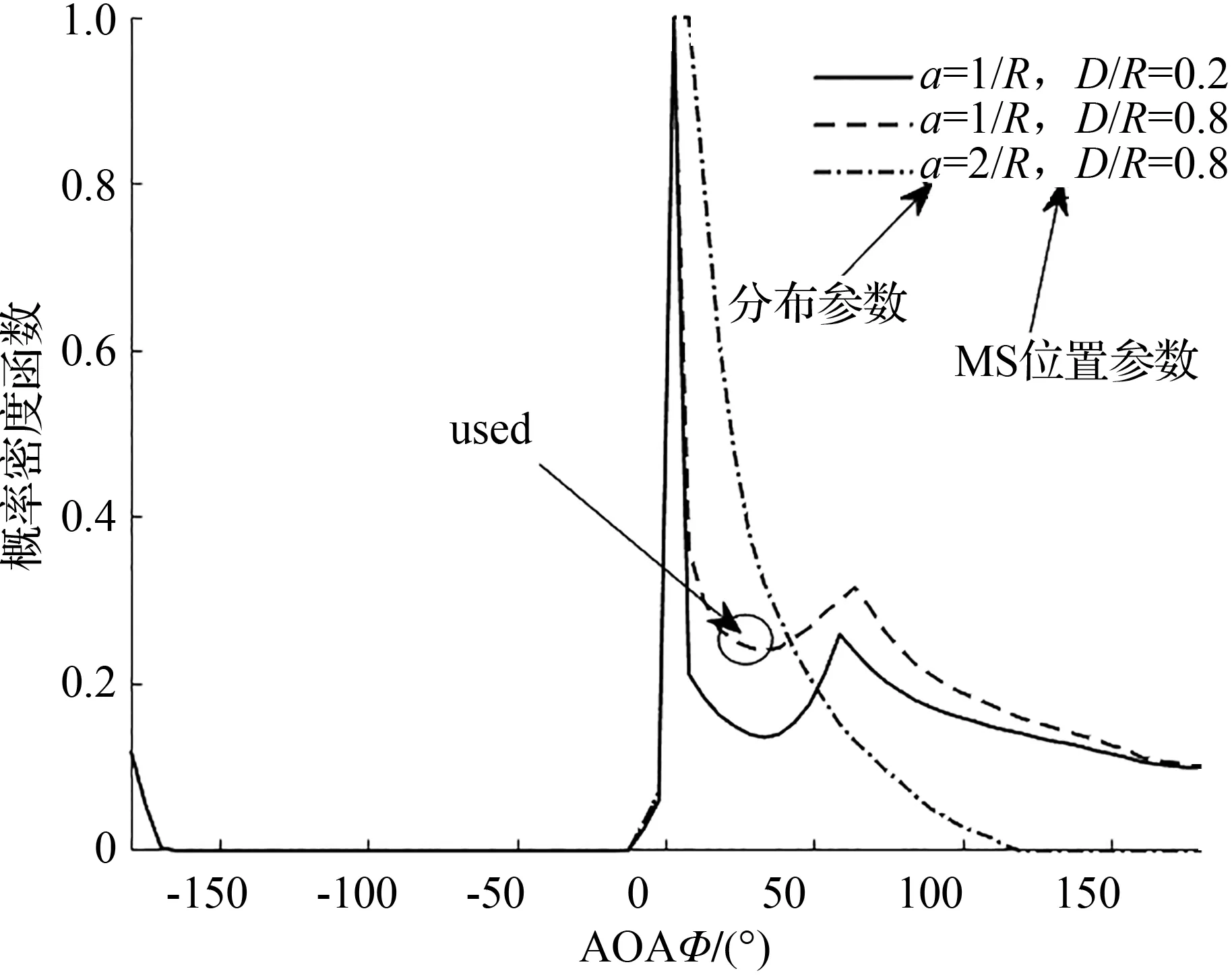
图2 非对称几何模型分布函数Fig.2 Distribution function of asymmetric geometry model

图2中的采样基函数拟合结果如图3所示，图3(a)中给出无互耦效应时采样间隔取不同值对应的相关性结果，图3(b)为采样点数一定时，有互耦效应和无互耦效应时的空域相关性，ZL=50 Ω。图3中的结果表明：①拉普拉斯分布和高斯分布采样函数模型的仿真曲线与理论曲线非常接近，明显优于均匀分布的采样结果；②有互耦效应时的空域相关性围绕着无互耦时的空域相关性曲线波动，总体上呈现降相关的趋势。

(a)采样点数不同时的空域相关性曲线(无互耦)

以不考虑天线单元间的互耦效应的情况为例，图4中给出不同采样间隔且AoA不同分布下的简化模型与理论值之间的绝对误差。绝对误差的计算公式为：ME=|ρ-ρt|。由图4(a)与图4(b)对比可得：①采样脉冲数目越小即角域扩展更大时，绝对误差越大，但其误差均可满足实际应用要求；②从图4(b)中可以清晰地看出天线间距较小时，绝对误差较大，表明若想获得较小的误差，在天线阵列排列时间距不应太紧凑；③AoA高斯分布简化模型与拉普拉斯分布简化模型与理论值更接近，在实际设计场景中可以选择高斯分布或者拉普拉斯分布简化模型。

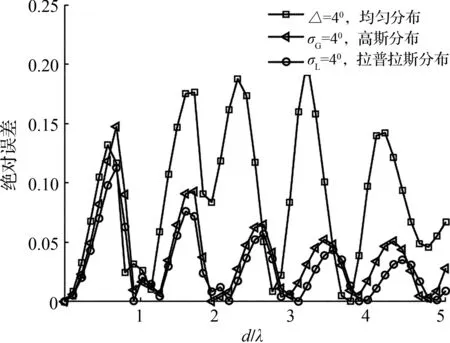
(a)角域扩展为4°时的绝对误差

图5所示为高斯分布下的简化模型在阵元间互耦与非互耦下的信道容量，图5(a)为d/λ=5，Nt=18，Nr=18，φ与信噪比变化时的信道容量，从图5(a)中可以看出考虑互耦效应时的信道容量比无互耦时的信道容量多接近40/bit/s/Hz；图5(b)为图5(a)的三维变化图，从图5(b)中可以看出，随着信噪比的增大，信道容量也随之增加，但增长趋势逐渐减缓，信噪比较小时，信道容量的增长速度更快；图5(c)与图5(a)区别在于d/λ的取值不同，图5(c)中的天线间隔更小，相关性更高，导致信道容量小于图5(a)中的信道容量；图5(d)中的天线间隔设置与图5(a)相同，而收发两侧的天线数量设置为8×8，与图5(a)相比，系统的信道容量更小，证明Massive MIMO中设置大量的天线可以大幅度提高系统的信道容量。

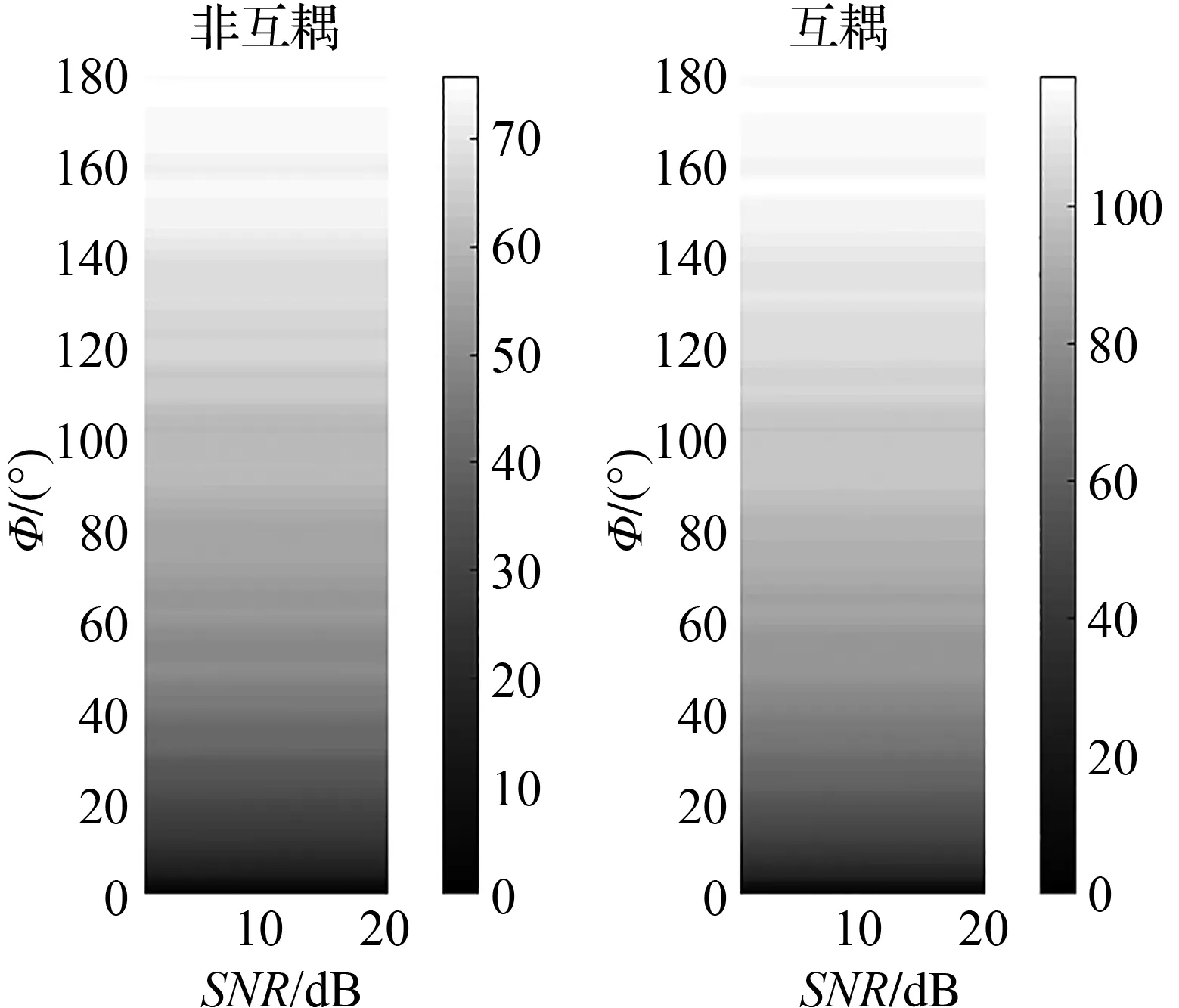
(a)d/λ=5,Nt=18,Nr=18

(c)d/λ=1,Nt=18,Nr=18

以上仿真结果证明本研究提出的简化分析模型能够很好地拟合全向小区非对称几何模型的AoA功率谱分布，对于其他模型也具有适用性，在接下来的小节中将针对实测AoA功率谱分布进行讨论，将本研究的简化计算模型推广到实际场景应用中。

3.2 实测AoA

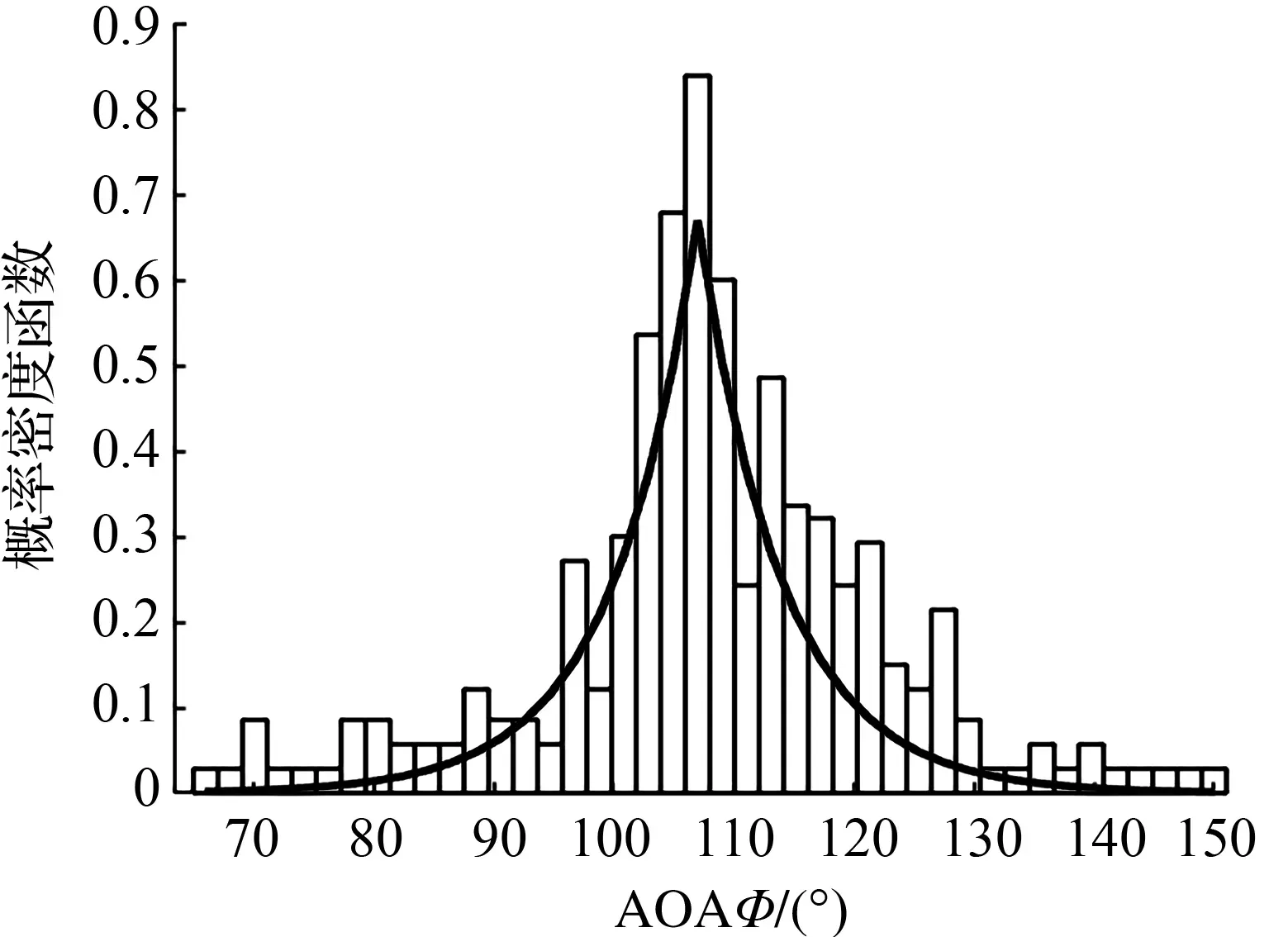
图6 城市街道入射角实测 Fig.6 Measured AOA of urban street

本研究以参考文献[20]中城市街道中实测非视距传播场景下的AoA功率谱分布为例，对本文提出的简化计算模型进行性能分析，城市街道入射角实测如图6所示，由图6可见，图6中的城市街道入射角实测数据拟合整体上近似服从截断拉普拉斯分布。

使用本文提出的基函数采样的方法对图6数据进行拟合，获取其空域衰落性相关性曲线[21]，实测AOA分布空域相关性曲线如图7所示。图7(a)中ZL=50 Ω，L取值不同时即采样点数不同时的空域相关性曲线，上侧为L=42，Δ/σ=2°，下侧为L=14，Δ/σ=6°。采样点数较多时，该简化模型可以很好地拟合数值积分的结果，而采样点数越少，数值积分与简化模型之间的误差越大，但均在合理的范围内，此外，从图中可以得出，随着d/λ比值的增大，天线间的相关性逐渐减小，这是因为随着天线间距的增加，阵元之间的互耦效应逐渐下降，影响变小，所以，若想减小相关性的影响在设计天线阵列时可适当增加阵元间距；图7(b)中L=14，从图7(b)中可以看出，有互耦效应时，天线间的相关性低于无互耦的情况，与参考文献[1-2]中的结论一致。

(a)采样点数不同时的空域相关性(考虑互耦效应)

表1为简化模型理论结果的绝对误差。从表1中可以看出，与数值积分的结果对比高斯分布和拉普拉斯分布的简化模型的绝对误差更小，均匀分布的绝对误差更大一些。在实际应用场景下可以根据绝对误差的大小，选择合适的AoA分布，减小绝对误差。表2为本文方法与数值积分方法及参考文献[17]方法在相同AOA分布下仿真时间结果对比。从表2中可以看出，本文模型计算时间短，与其他方法相比计算效率更高。

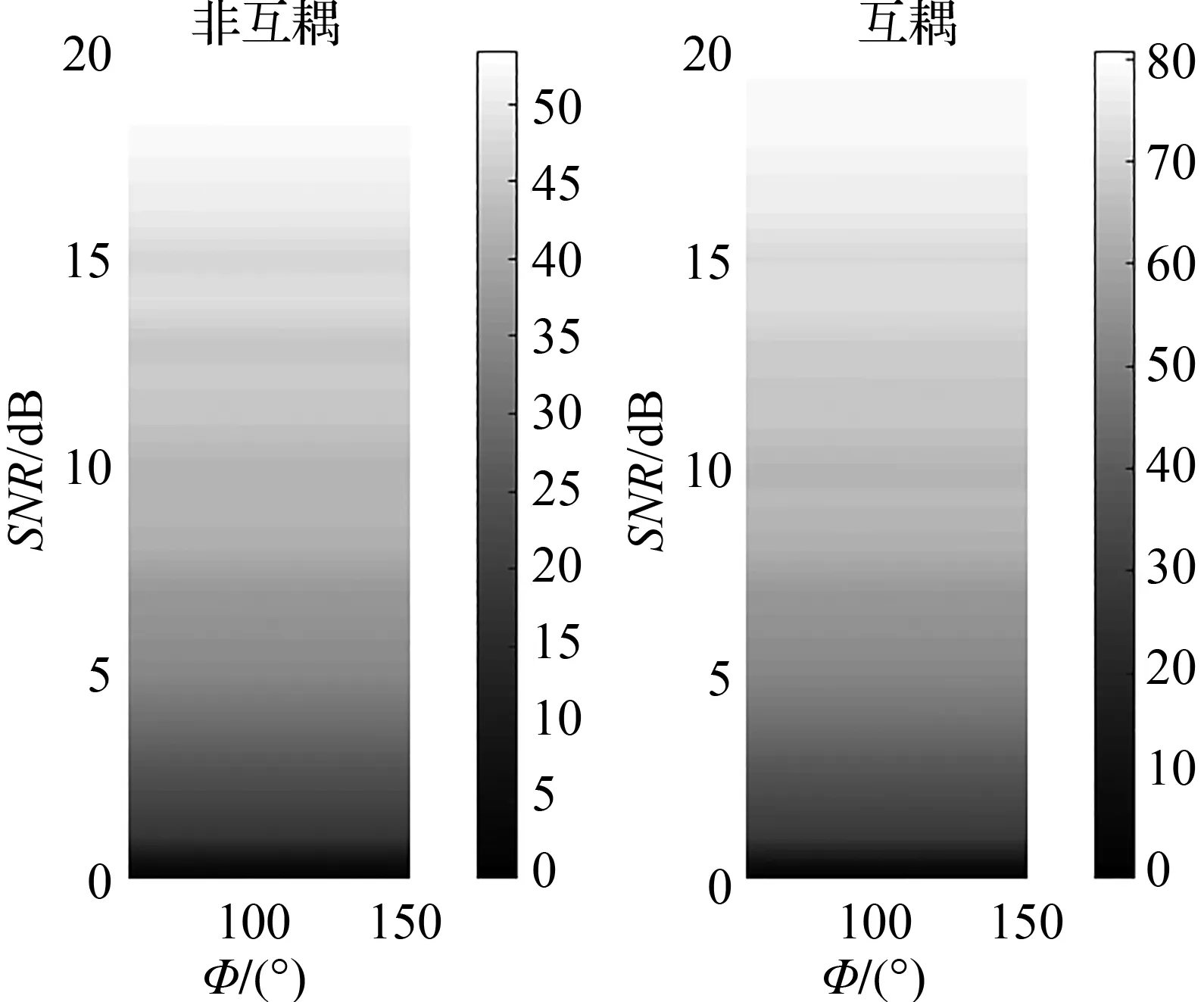
图8为AoA高斯分布下，阵元间互相耦合与无耦合情况下的系统容量对比。从图8(a)、图8(c)中可以看出，当d/λ=5且收发两端天线数量为18×18时，不考虑互耦效应的信道容量最大值接近60/bit/s/Hz，而存在互耦效应时，信道容量最大值超过了80/bit/s/Hz，说明互耦效应可以增加一定的系统容量，与文献[5-7]中关于互耦效应对系统容量的影响结果一致，此外，图8(a)表明，随着水平面角 的增长，信道容量也是增长的。同样地，图8(c)表明总体上信道容量随着信噪比的增大而增大，但信道容量不是个无限增大的，最终会趋近于一个定值。图8(b)表明，信道容量在天线单元之间有互耦效应和相互独立无互耦时的增长趋势相似，最终增长趋势比较缓和。区别于图8(a)，图8(d)中d/λ=1，而天线数量不变，明显可以看出，图8(d)中系统容量都更小，表明d/λ比较小时，空间衰落相关性更大，系统容量更小，而图8(d)与图8(e)相比，d/λ的值相同但天线数量不同，图8(e)中的天线数量为8×8，表明系统容量会随着天线数量的增加而增加，但天线数量持续增长时，系统容量增加的倍数也会减小，最终趋于稳定。

表1 绝对误差均值Tab.1 Mean absolute error

表2 运算时间Tab.2 Calculating time

本小节的仿真结果表明，本研究提出的简化模型适用于实际场景下的AoA功率谱分布，且符合前人研究中得出的结论，结合4.1节可得，对于天线单元间独立同分布及考虑互耦效应下的任意AoA功率谱分布，本文提出的简化计算模型都能很好的拟合，获取空域相关性曲线。

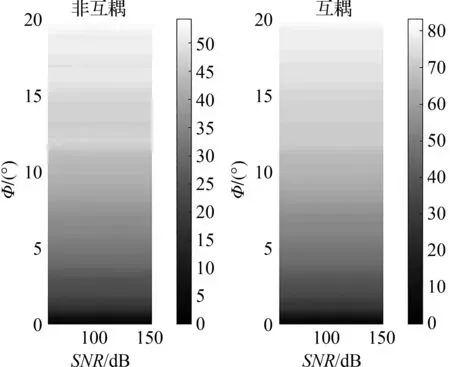
(a)d/λ=5,Nt=18,Nr=18,φ取不同值

(c)d/λ=5,Nt=18,Nr=18，SNR取不同值

(e)d/λ=1,Nt=8,Nr=8，φ取不同值

4 结语

本文提出了阵元间相互独立与相互耦合两种情况下的AoA功率谱简化模型，推导出该模型在不同AoA分布下的闭式表达式。通过MATLAB软件实现的仿真结果，对该模型与非对称几何信道及实际场景下的AoA功率谱数据进行拟合、对比，得出本文提出的模型与理论信道模型及实际场景能够很好的拟合，适用于任意场景下的AoA功率谱分布，并对不同条件下的信道容量进行了分析，得出阵元间的互耦效应可以提高系统的信道容量。在Massive MIMO系统设计时选择合适的天线间距可以降低空域相关性，提高系统性能，增加系统容量，提高频谱资源利用率。