米波MIMO雷达波束空间精确最大似然算法
2022-05-07赵永波庞晓娇胡毅立曹成虎
陈 胜, 赵永波, 庞晓娇, 胡毅立, 曹成虎
(西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)
0 引 言
米波雷达因其具有反隐身、抗反辐射导弹等独特优势,近年来受到了世界各国越来越多的重视。在米波雷达跟踪低空目标时,目标直达信号和多径信号同时从波束主瓣进入天线,并且这两路信号在时域和频域均无法被分开,不仅影响信号检测性能,还严重影响目标的仰角估计性能。
能够有效进行低仰角估计的方法主要分为两类:特征子空间类算法和最大似然类算法。特征子空间类算法对快拍数和信噪比的要求较高,并且不能直接处理相干信号,空间平滑算法能对信号进行解相干处理,但是天线有效孔径会有损失。最大似然类算法通常需要进行多维空间谱搜索,尤其是对于大型阵列雷达,处理过程仍需上百个阵元的协方差矩阵计算,运算量和数据传输量都很大,不利于工程实现。利用交替投影算法可以有效降低运算量;利用低角跟踪中的几何关系,可将多径信号仰角表示为直达信号仰角的函数,从而将二维空间谱搜索降为一维空间谱搜索,减小运算量,并提高测角精度。文献[18]提出了精确最大似然(refined maximum likelihood,RML)算法,利用了反射系数的先验信息,并用多径条件下复合导向矢量代替自由空间中的常规导向矢量,即采用精确多径模型,再利用最大似然方法进行目标仰角估计。该算法待估计参数少,在减小运算量的同时也提高了测角精度。
通过增加雷达的天线孔径能够有效提高测角精度,但常规相控阵雷达受实际条件限制,天线孔径不可能做得很大。多输入多输出(multiple input multiple output,MIMO)雷达是近年来被国内外学者大量研究的新体制雷达。MIMO雷达具有孔径扩展的优势,从而能够提高雷达的角分辨率和测角精度,但其带来的问题是运算量和数据传输量十分巨大,工程实现有很大难度。
基于波束空间的处理相当于对阵列接收的数据做一次预处理,将阵元空间的数据转换到波束空间,实现降维处理,再对波束空间的数据进行仰角估计,因其具有运算量低和数据传输量低的优点,近年来受到了普遍的关注。本文提出了一种基于波束空间的MIMO雷达RML算法,该算法采用MIMO雷达精确多径模型,将阵元空间的数据转换到波束空间,再利用RML算法对波束空间的数据进行测角,不仅有着良好的测角性能,还大大降低了运算量与数据传输量。
1 信号模型
MIMO雷达低角跟踪环境下的多径几何模型如图1所示。假设MIMO雷达收发天线共用,天线为阵元间距为的等距线阵,阵元数为,图中和分别表示目标高度和天线中心高度,和分别表示目标到雷达的直达距离和因反射而形成的多径距离,表示目标仰角,代表多径信号仰角。MIMO雷达接收到来自4条路经的信号,其中包括:第1条是发射信号直接到达目标,经目标直接反射到接收天线的信号,第2条是发射信号经地面反射后到达目标,再经目标直接反射到达接收天线的信号,第3条是发射信号经目标,再经地面反射到接收天线的信号,第4条是发射信号经地面反射到目标,再经地面反射到接收天线的信号。
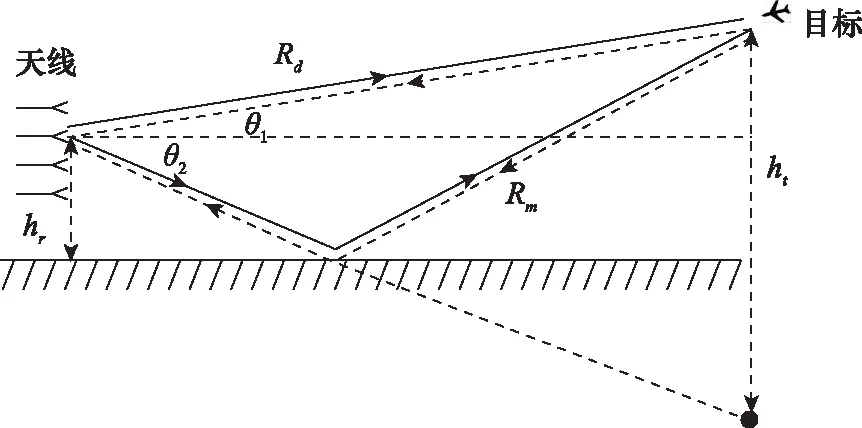
图1 MIMO雷达低角跟踪环境下的多径几何模型Fig.1 Multipath geometry model of MIMO radar in low angle tracking scenario
MIMO雷达接收的阵列信号可表示为
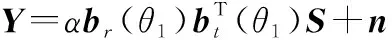
(1)
式中:为信号的复幅度;为波形矩阵;为复高斯白噪声,与信号不相关,其噪声方差Var()=,表示其方差值大小,表示单位矩阵;()和()分别为复合接收导向矢量和复合发射导向矢量,表达式分别为

(2)

(3)

由图1可以看出,直达信号仰角与多径信号仰角之间存在着几何关系,结合天线中心高度的信息,可以得到
=-arcsin(sin()+2)。
(4)
2 MIMO雷达RML算法
MIMO雷达RML算法采用精确多径模型,并分别对发射和接收进行处理获得的虚拟孔径扩展特性,形成更窄的接收波束,提高系统仰角估计精度。下面分别对基于阵元空间的MIMO雷达RML算法和基于波束空间的MIMO雷达RML算法进行介绍。
2.1 基于阵元空间的MIMO雷达RML算法
基于阵元空间的MIMO雷达RML算法在精确多径模型的基础上利用最大似然方法对阵元空间的目标数据进行仰角估计。该算法的基本步骤如下。
对阵列接收数据进行匹配滤波,即
=
(5)
式中:为快拍次数。
根据最大似然的思想,可得此时的似然函数值,即
()=
(6)
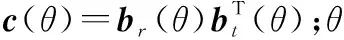
根据式(6)计算的似然函数值可得目标仰角估计值,即
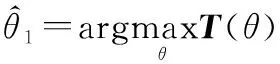
(7)
2.2 基于波束空间的MIMO雷达RML算法
基于阵元空间的MIMO雷达RML算法具有较高的估计精度,但同时存在运算量和数据传输量十分巨大的问题,很难应用到工程上。基于波束空间的MIMO雷达RML算法首先将阵元空间的数据转换到波束空间,只需要对波束空间的数据进行传输,然后利用最大似然方法对波束空间的数据进行仰角估计。
基于波束空间的MIMO雷达RML算法的基本步骤如下。
预设3个分别指向为、0°、-的发射波束转换矢量,即
()=
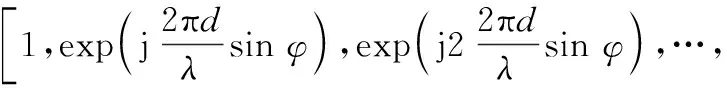
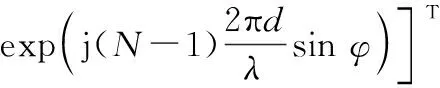
(8)
(0)=
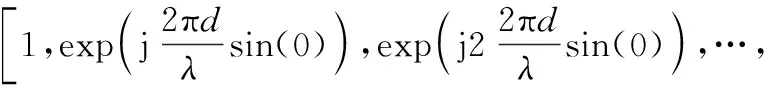
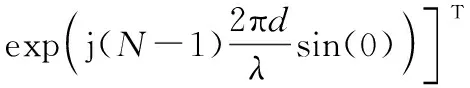
(9)

(10)
预设3个分别指向为、0°、-的接收波束转换矢量,即
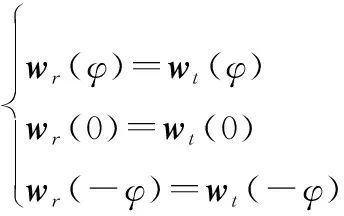
(11)
利用波束转换矢量将阵列接收的数据转换到波束空间,即
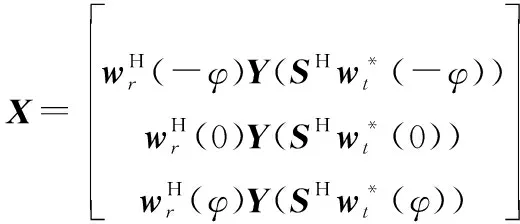
(12)
利用波束转换矢量将用于搜索的复合导向矢量转换到波束空间,即
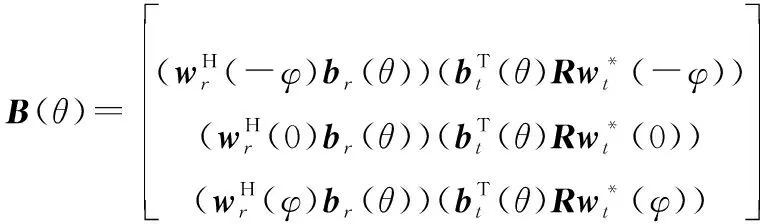
(13)
式中:=为发射波形相关矩阵。
根据最大似然的思想,可得此时的似然函数值,即
()=
(14)
式中:=()[()()]()为投影矩阵。
根据式(14)计算的似然函数值可得目标仰角估计值,即
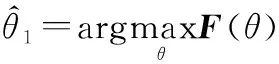
(15)
将阵元空间的数据转换到波束空间,一方面降低了自由度,导致测角精度有所降低,但只要波束的维度大于信源个数即可对目标仰角进行估计;另一方面,由阵元空间到波束空间的转换实际上是通过多个波束合成实现的,波束合成有着增强信号功率的作用,这在一定程度上能够弥补自由度降低带来的损失。
基于阵元空间的MIMO雷达RML算法的计算复杂度为(+),其中为仰角搜索值个数,基于波束空间的MIMO雷达RML算法的计算主要包括3部分,分别为将阵元空间的数据转换到波束空间、将阵元空间用于搜索的复合导向矢量转换到波束空间和计算似然函数值,这3部分的计算复杂度分别为()、()和(),所以该算法总的计算复杂度为(+),明显小于基于阵元空间的算法计算复杂度。
3 计算机仿真
本节通过阵元空间与波束空间MIMO雷达RML算法的计算机仿真对比实验,对所提算法的测角精度、运行效率和稳健性能进行了分析,其中包括信噪比、目标仰角、波束指向与目标仰角之间的偏差、阵元数、反射系数误差和天线中心高度等因素对所提算法测角性能的影响。仿真所用信噪比为接收直达波检测信噪比,定义为
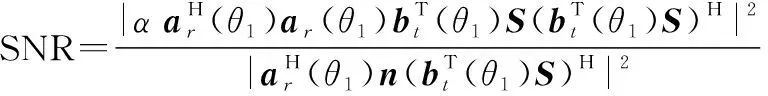
(16)
假设雷达天线在垂直面上为一均匀等距线阵,收发天线共用,波束指向为直达波信号方向,仿真所用的系统参数如表1所示,目标参数如表2所示,蒙特卡罗试验次数为1 000次,在具体的仿真中若参数有变化会给出说明。

表1 系统参数

表2 目标参数
首先对这两种算法的测角精度进行对比分析。图2为这两种测角算法的均方根误差随直达波检测信噪比的变化曲线。从图2中可以看出,当信噪比较低时,所提算法的测角精度相对于MIMO雷达阵元空间RML算法的测角精度有着一定的损失,当信噪比较高时,所提算法的测角精度相对于MIMO雷达阵元空间RML算法的测角精度基本没有损失。这两种算法测角均方根误差随目标仰角的变化曲线如图3所示。从图3中可以看出,当仰角比较低时,所提算法的测角精度相对于MIMO雷达阵元空间RML算法的测角精度有着一定的损失,当仰角较高时,所提算法的测角精度相对于MIMO雷达阵元空间RML算法的测角精度基本没有损失。此外,当仰角比较低时,两种算法的测角误差都较大,这是因为此时直达信号与多径信号在空间上非常接近,而反射系数是负的,导致直达信号与多径信号相互抵消。假设天线阵元数的变化范围为10~60,图4为这两种算法测角均方根误差随阵元数的变化曲线。从图4中可以看出,当阵元数较少时,所提算法的测角精度相对于MIMO雷达阵元空间RML算法测角精度的损失较小,当阵元数较多时,所提算法的测角精度相对于MIMO雷达阵元空间RML算法测角精度的损失稍大一些,这是由于此时自由度的损失较大导致的。
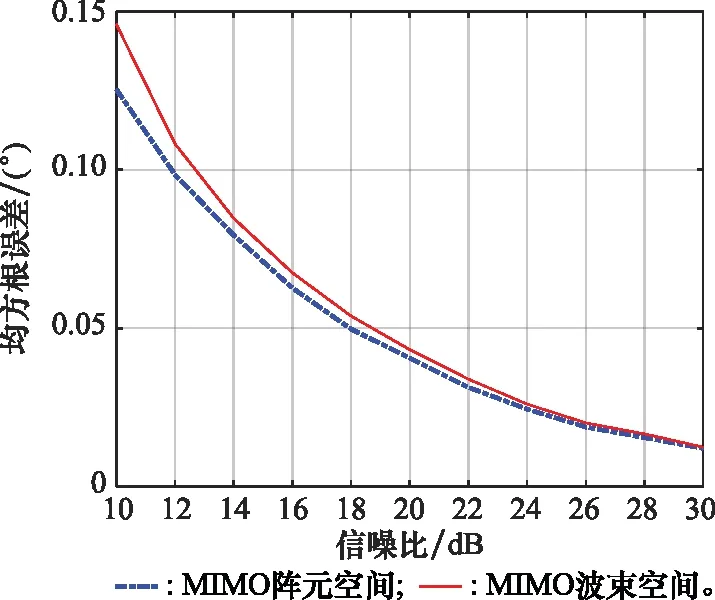
图2 信噪比对误差的影响分析Fig.2 Influence analysis of signal to noise ratio on error
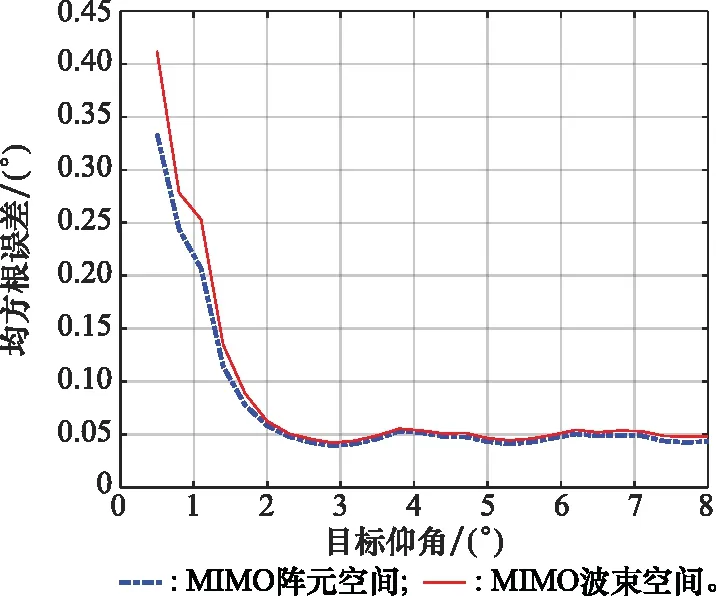
图3 仰角对误差的影响分析Fig.3 Influence analysis of elevation angle on error
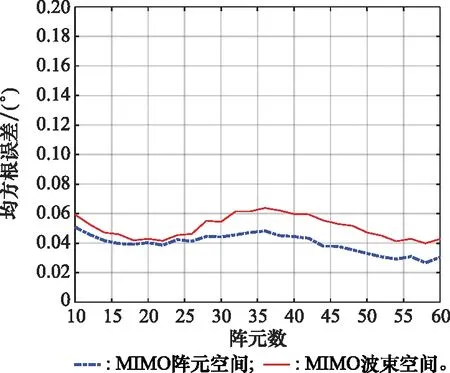
图4 阵元数对误差的影响分析Fig.4 Influence analysis of elements number on error
然后对这两种算法的运行效率进行分析。这两种算法的运行时间随阵元数的变化曲线如图5所示,其中阵元空间的复合导向矢量、波束转换矢量和发射波形相关矩阵均已提前计算好,两种算法的运行时间分别包括式(5)~式(7)和式(12)~式(15)。从图5中可以看出,与MIMO雷达阵元空间RML算法相比,所提算法大大降低了运行时间,与前面计算复杂度的分析结果是一致的。同时,由于将目标数据转换到了波束空间,极大地降低了数据传输量。
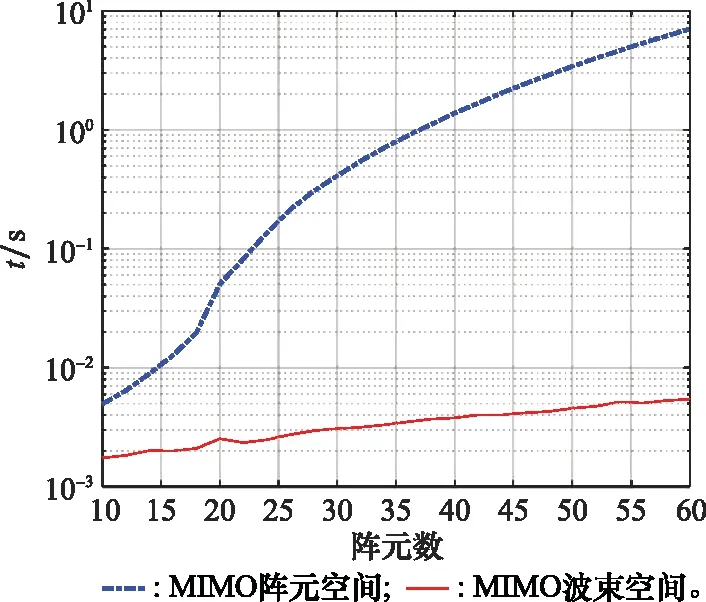
图5 阵元数对运行时间的影响分析Fig.5 Influence analysis of elements number on running time
最后对这两种算法的稳健性能进行分析。假设直达波检测信噪比分别为20 dB和30 dB,波束指向与目标仰角之间存在偏差,图6为所提算法测角均方根误差随偏差角度的变化曲线。从图6中可以看出,当直达波检测信噪比为20 dB时,在个别情况下波束指向与目标仰角之间存在偏差会导致测角性能恶化;当直达波检测信噪比为30 dB时,波束指向与目标仰角之间存在偏差对所提算法的测角性能几乎没有影响。
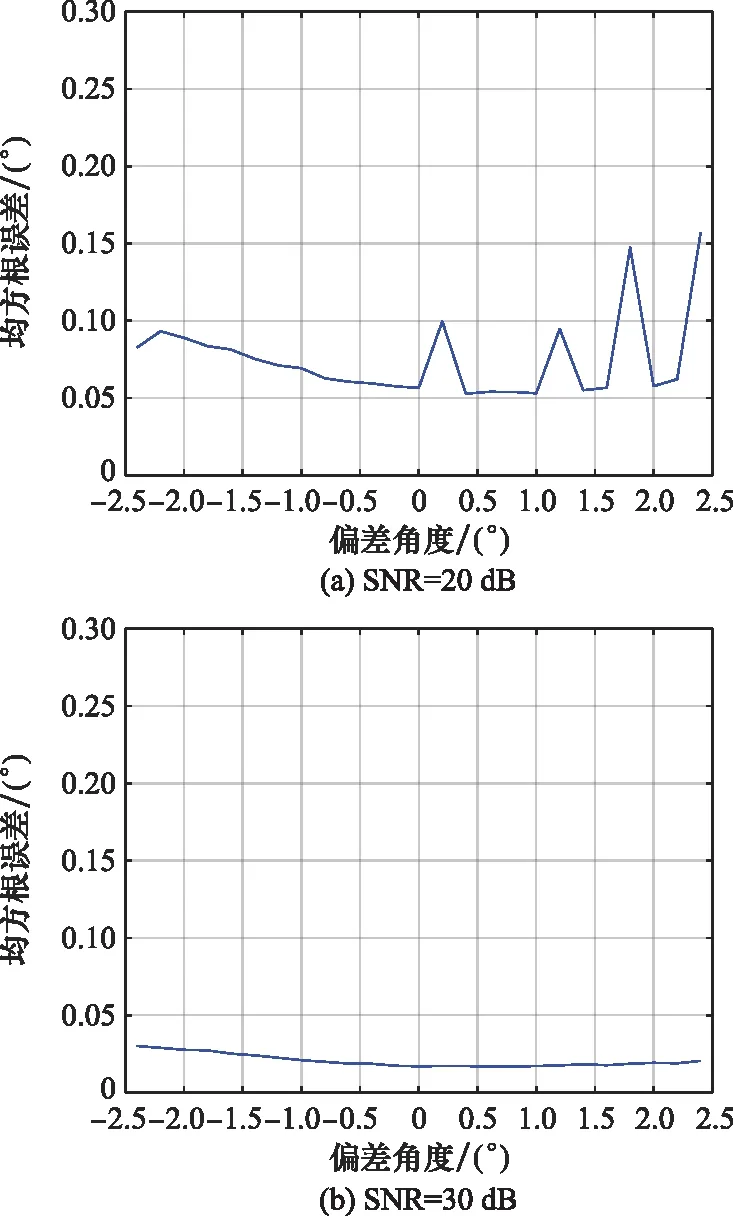
图6 偏差角度对误差的影响分析Fig.6 Influence analysis of deviation angle on error
下面假设反射系数存在误差,此时两种算法测角均方根误差随直达波检测信噪比的变化曲线如图7所示,其中反射系数幅度的真实值为0.9,相位真实值为π。从图7中可以看出,无论是在阵元空间还是在波束空间对目标进行测角,反射系数幅度误差对测角性能的影响都很小,而反射系数相位误差对测角性能的影响都很大。

图7 ρ存在误差的影响分析Fig.7 Influence analysis of ρ error
下面假设天线中心高度分别为7 m和9 m,不同天线中心高度情况下两种算法测角均方根误差随直达波检测信噪比的变化曲线如图8所示。从图8中可以看出,当天线中心高度为7 m时,两种算法都能够正常测角,当天线中心高度为9 m时,基于阵元空间的MIMO雷达RML算法仍然能够正常测角,但基于波束空间的MIMO雷达RML算法的测角误差大幅增加,这是因为此时天线中心高度较高,出现了仰角模糊的现象,下面对仰角模糊的问题进行仿真分析。不考虑噪声的影响,两种算法的扫描曲线如图9所示。从图9中可以看出,当天线中心高度为7 m时,两种算法的扫描曲线在主瓣附近只有一个峰值,此时能够正常得到仰角估计值,当天线中心高度为9 m时,基于阵元空间的MIMO雷达RML算法扫描曲线的第一副瓣虽然有所升高,但不会影响测角结果,而基于波束空间的MIMO雷达RML算法的扫描曲线副瓣高度与主瓣高度十分接近,很容易出现仰角模糊的现象,导致测角误差增加。
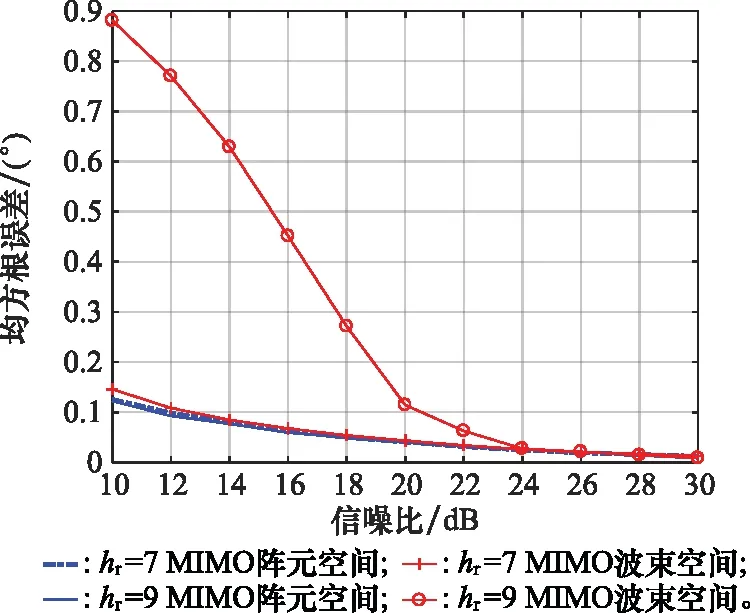
图8 天线高度对误差的影响分析Fig.8 Influence analysis of antenna height on error
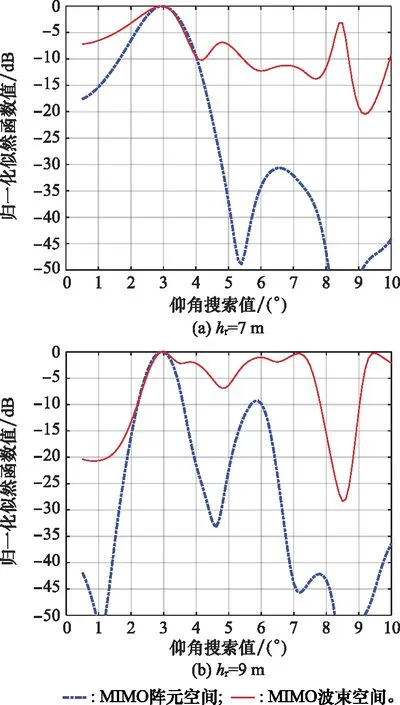
图9 扫描曲线Fig.9 Scanning curve
4 结 论
本文针对阵元空间MIMO雷达低仰角估计方法运算量和数据传输量太大的问题,提出了一种基于波束空间的MIMO雷达RML算法。该算法首先将阵元空间的数据转换到波束空间,再根据最大似然的思想进行测角。该算法与基于阵元空间的MIMO雷达RML算法相比不仅有着良好的测角性能,也大大降低了算法运算时间,同时由于对数据进行了降维处理,也减小了数据传输量,并且波束指向与目标仰角之间的偏差对算法测角性能的影响不大。需要注意的是,该算法对天线中心高度十分敏感,当天线中心高度稍高一些时,仰角模糊的现象会比较严重,导致测角性能降低。
