考虑维修场所的动车组多部件双目标成组维修研究

齐彦昆，王 红，何 勇，熊 律

（兰州交通大学机电工程学院，甘肃 兰州 730070）

在以维修成本和维修时间为导向的维修体系下，影响动车组预防性维修策略制定的因素越来越受到重视。维修场所作为承担动车组检修任务的基地，各部件的维修操作需依托其展开，且维修的效果、成本和时间与维修场所内维修方式的选择和维修任务的分配直接关联。因此，如何考虑维修场所因素以统筹规划维修策略，实现动车组维修成本和维修时间的优化已成为亟待解决的问题。

目前，针对多部件系统的维修，主要通过对部件衰退过程的描述来判断维修时机，并结合成组维修策略制定方案［1-4］。Fan等［5］针对部件维修时机离散化的现象，采用成组维修策略将各部件单独的预防性维修计划进行整合；Yang等［6］采取定周期的成组维修策略，既便于操作，又有效节约了停机成本；Shafiee等［7］采用更换的方式对部件进行成组维修，并在系统达到预定役龄时对其所有部件执行更换操作。但是，文献［5-7］均采用单一的维修方式，其维修策略不能较好地匹配动车组的多级维修机制。为此，王红等［8］采取具有初级维修和高级维修的两级非完美维修方式对动车组部件进行维修；刘志龙等［9］考虑不同维修方式下所需成本和维修效果的差异，基于效费比的概念对动车组部件的维修方式进行选择。

现有维修策略的成本模型大多重点关注维修操作和停机损失所带来的成本，但这并不全面。动车组的维修作业通常在动车所内实施，需要提前准备设备、人员等维修资源。且有时为使部件恢复更佳的性能状态，动车组须前往动车段维修，限于动车段数量较少且辐射范围较广，维修时需调动车组前往动车段所在地，此类操作均有相应成本产生。因此，忽略维修场所来衡量维修策略制定的经济性并不合理。

此外，在追求维修策略经济性的同时，也应尽可能地缩短维修时间［10-12］。狄鹏等［13］在制定维修策略时，将部件维修时间纳入考虑，通过优化机会维修阈值来获取系统的最优维修成本和可用度，但其对维修时间的研究停留在部件层面，缺乏对系统层维修时间的考虑。王正元等［14］将维修人员视为承担部件维修任务的主体，通过对维修任务和维修人员的优化匹配，实现了系统维修时间最短，但其并未考虑维修人员在不同维修方式下所需时间的差异。

为此，笔者提出了一种考虑维修场所的动车组多部件双目标成组维修策略。首先，在预防性维修中采用两级非完美维修方式，并引入维修场所对维修方式的约束，通过维修场所的选择进一步选择维修方式；然后，提出一种部件维修任务分配算法，通过对维修人员和部件维修任务的优化匹配来实现系统维修时间最短；最后，将所提出的算法引入到遗传算法中，以优化求解动车组系统的维修成本和维修时间。

1 动车组系统维修问题描述与假设

以动车组多部件系统为研究对象，四级修运行里程区间为研究范围。随着运行里程的增加，动车组系统的部件会逐渐老化，有必要根据维修策略进入相应的维修场所实施维修作业。维修时因受到维修人员数量的限制，无法同时维修各部件，须将待维修部件分配至相关维修人员依次进行维修。基于此，针对所研究的内容，提出以下假设：

1）动车组系统的部件由全新状态投入运行。

2）在维修方式上，采取具有初级维修和高级维修的两级非完美维修方式。

3）维修时机选取动车组二、三级修里程点。由于各部件的二级修时机不同，为简化模型，统一选取2×105km作为单位维修里程。

4）小修不改变部件的可靠度和衰退速率，仅消除部件的故障状态。

5）部件维修流程工序规范化，维修时间和维修成本均为定值。

6）以“1 h”为单位维修时间。

2 动车组部件层预防性维修策略建模

2.1 可靠度阈值限制

为确保动车组系统的部件运行状态良好，故障风险可控，设置部件j（j=1，2，…，m）的可靠度阈值为Rjmin。要求在动车组运行区间内，各部件的时变可靠度Ri，j（i=1，2，…，n，j=1，2，…，m）均高于Rjmin，即满足可靠度阈值限制，可表示为：

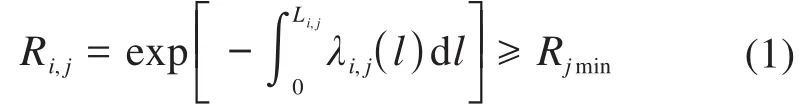
式中：Li，j为部件j第i-1次至第i次预防性维修间的运行里程；λi，j(l)为部件j第i-1次至第i次预防性维修间的故障率函数；l为本次运行区间内任意时刻对应的里程。

2.2 故障率演化建模

威布尔分布（Weibull distribution）广泛应用于机械设备的可靠性计算，适用于描述机械设备的衰退过程。本文基于双参数威布尔分布对动车组系统各部件的故障率演化规律进行描述。部件j由全新状态投入运行至第1次预防性维修间的故障率函数λ1，j(l)可表示为：

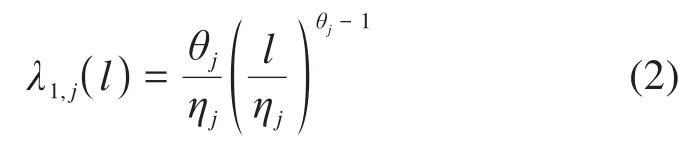
式中：θj为部件j的形状参数；ηj为部件j的生命特征参数。

为表征维修活动在故障率演化过程中所起的作用，Zhou等［15］结合文献［16-17］提出了混合故障率演化模型，用于描述维修操作对故障率函数的影响，可表示为：

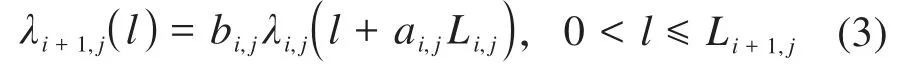
式中：bi，j、ai，j分别为部件j第i次预防性维修后的故障率递增因子和役龄回退因子。

在维修方式上，本文在原有单级非完美维修的基础上，结合我国动车组现行的多级修制，采用具有初级维修和高级维修的两级非完美维修方式：将原属于运用检修的二级修视为初级维修，属于定期检修的三级修视为高级维修。因受维修设施、时间等因素的影响，高级维修的效果明显优于初级维修，如图1所示。

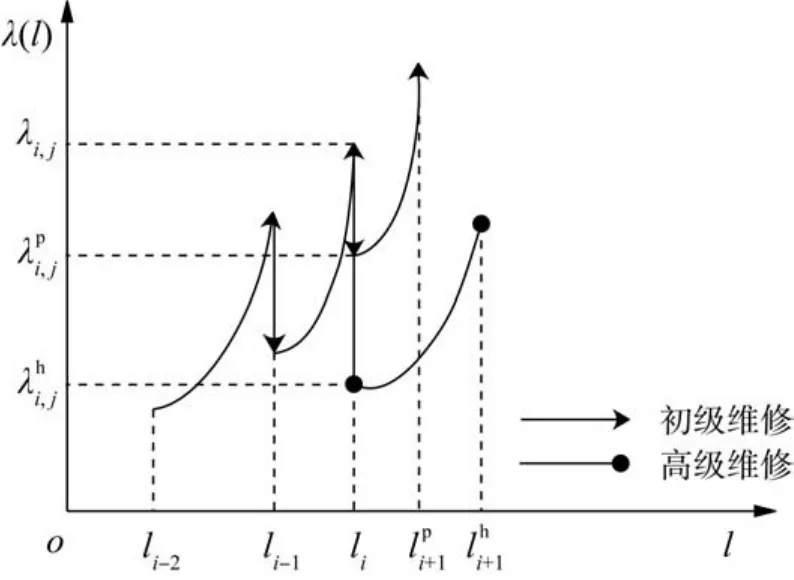
图1 初级维修与高级维修效果比较Fig.1 Comparison of effect of primary maintenance and advanced maintenance

为便于选择，引入维修方式选择因子χi，j：

根据选择因子χi，j取值对部件采取相应的维修方式。由于维修方式不同，维修后部件的故障率递增因子和役龄回退因子也不同，故对其进行修正：

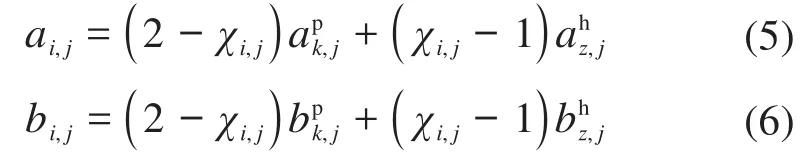
3 动车组系统层维修策略研究

3.1 系统层维修模型

相较于传统的机械系统，动车组系统维修策略的制定受多方面因素的影响。第一，在维修方式上，动车组具有多级修程，且各级修程的修复效果呈递增趋势；第二，在维修场所上，根据维修职能的不同，可分为动车所和动车段两级，动车所仅有运用车间，动车段兼有运用车间与高级修车间；第三，维修场所对维修方式具有约束作用，即初级维修在运用车间实施，高级维修在高级修车间实施，可表示为：

式中：Su为第u次动车组系统停机时维修场所选择因子；G为维修方式集，G1={0}，G2={0，1}，G3={0，1，2}。

综合考量上述特点，本文采取间接成组维修策略，以L为单位运行里程，将动车组系统维修规划期划分为多段，动车组于每段单位运行里程末尾的节点处有维修的机会，各部件维修方式的选择与该节点处维修场所的选择有关。当动车组的累计运行里程达到四级修里程时，对动车组系统实施大修。如图2所示，L，2L，…，qL为动车组维修时机。当运行里程为L时，动车组不前往维修场所，各部件不进行维修；当运行里程为3L时，动车组前往动车所，各部件选取G2中的维修方式；当运行里程为qL时，动车组前往动车段，各部件选取G3中的维修方式。

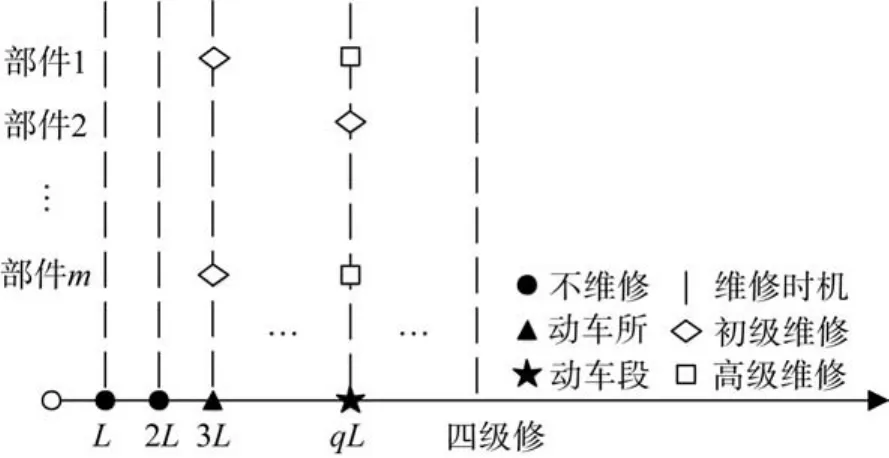
图2 不同运行区间内动车组系统的维修策略Fig.2 Maintenance strategy of electric multiple unit system in different operation intervals

3.2 系统维修成本

3.2.1 部件层维修成本

部件层维修成本主要包括预防性维修成本和故障小修成本。

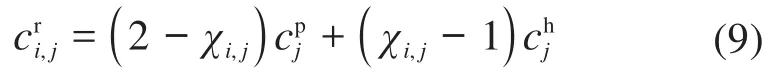
综上，动车组系统在维修规划期内的部件层维修成本Cg可表示为：

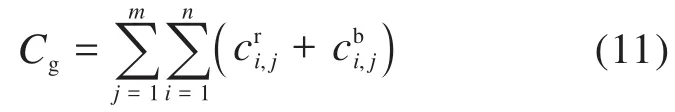
3.2.2 系统层维修成本

系统层维修成本Ch包括动车组前往动车段的调度成本、维修资源准备成本和维修人员雇佣成本，可表示为：

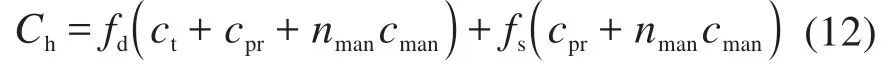
式中：ct为动车组前往动车段的调度成本；cpr为维修资源准备成本；cman为维修人员雇佣成本；nman为维修人员雇佣数量；fd、fs分别为动车组前往动车段、动车所的维修次数。

综上，维修规划期内动车组系统的总维修成本C可表示为：

3.3 系统维修时间

部件维修时间是指各部件根据维修计划进行预防性维修所需的时间。部件j第i次预防性维修所需的时间ti，j可表示为：

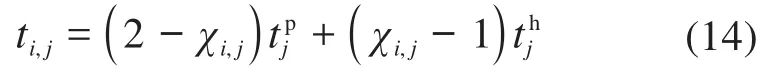
在动车所（段）内，维修作业通常由维修人员操作实施。通过对待维修部件依次进行维修，达到部件可靠度回升的效果。但限于维修人员数量往往小于待维修部件数量，不同部件的维修作业不能在同一时间段内进行，需分配给不同的维修人员；动车组系统的维修时间以最后完成维修作业的时间为准。鉴于所研究动车组系统中的部件数量有限，雇佣2名维修人员即可在较短时间内完成维修任务。则动车组系统第u次停机时的维修时间Tu为：

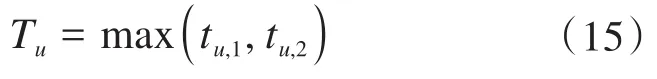
其中：

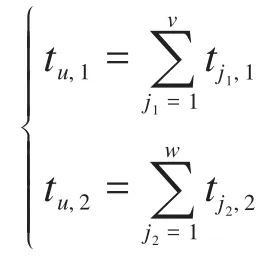
式中：tu，1、tu，2分别为动车组系统第u次停机时维修人员 1和维修人员2完成维修作业所需的时间；tj1，1、tj2，2分别为分配给维修人员1和维修人员2的待维修部件j1、j2的维修时间；v、w分别为分配给维修人员1和维修人员2的待维修部件数量。

综上，维修规划期内动车组系统的总维修时间T为：

式中：f为动车组系统停机次数，f=fs+fd。

3.4 目标函数

以维修成本和维修时间最小为优化目标，构建动车组多部件双目标成组维修优化模型：

在保证动车组系统各部件的时变可靠度高于可靠度阈值以及各部件维修在动车组维修时机上实施的前提下，对动车组系统进行多部件双目标成组维修。

4 动车组多部件双目标成组维修模型求解

4.1 基于动态规划的系统维修时间求解

当2名维修人员同时完成维修作业，即不存在一维修人员等待另一维修人员的现象时，维修时间Tu最优。但因受待维修部件数量和不同部件维修时间差异的影响，Tu的最优解的实现具有未知性。为获得动车组多部件双目标成组维修模型的实际解，从维修人员等待时间最小化的角度出发，将min(Tu)转化为min(|tu，1-tu，2|)进行求解，如图3所示。

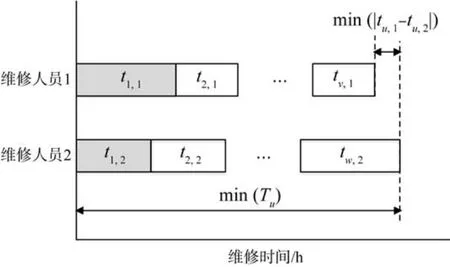
图3 动车组系统部件维修任务分配方案Fig.3 Maintenance task allocation scheme of electric multiple unit system components

基于上述分析，采取动态规划算法中的求子集和方法进行求解。然而，与传统求解思路不同的是，本文中维修任务分配问题的目标具有未知性。因此，应先从理论最优解，即tu，1-tu，2=0 附近寻求实际最优解，然后利用逆推法获得分配方案，具体流程如下。

步骤1 根据部件维修方式的选择确定部件的维修时间，并按维修时间长短对待维修部件依次排序；

步骤2 将优化目标由min(Tu)转化为min(|tu，1-tu，2|)；

步骤4 根据动态规划算法原理，构建逻辑判断矩阵并进行决策；

步骤5 寻求是否存在满足目标的方案，若存在，则执行步骤6，否则令ta=ta+tt(tt为单位维修时间，本文取tt=1 h)，并返回步骤4；

步骤6 采取逆推法求解具体分配方案，并输出系统维修时间Tu。

将基于动态规划的部件维修任务分配算法引入到遗传算法中，用于计算动车组系统的维修时间。

4.2 基于遗传算法的维修模型确定

考虑到维修场所对部件维修方式的影响，采取整数规划来描述维修模型，但该模型的求解复杂程度较高，且优化目标不单一，若采取传统的运筹学优化方法，则难以在短时内获得可行较优解。因此，本文采取多目标遗传算法进行求解。

1）编码与初始化种群。

为描述维修场所对维修方式的约束，将种群中每条染色体分为两部分：前半部分用于记录动车组对维修场所的选择，称为维修场所染色体；后半部分用于记录部件对维修方式的选择，称为维修方式染色体。维修场所染色体中的基因个数o为：

式中：Lmax为动车组系统维修规划期内的总运行里程。

维修方式染色体中基因个数e=oj。由于染色体基因以整数形式表示，采取实值编码法对染色体基因进行编码。基于维修场所对维修方式的约束，随机生成染色体以组成初始化种群，用于求解动车组系统维修模型，如表1所示。

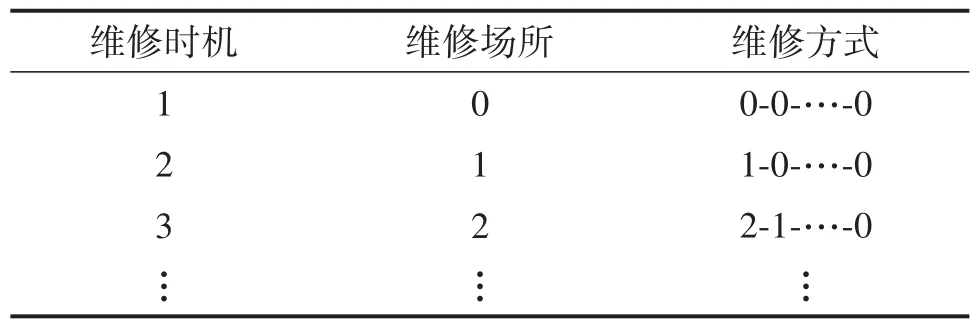
表1 用于求解动车组系统维修模型的初始化种群Table 1 Initialized population for solving electric multiple unit system maintenance model

2）交叉与变异。

在交叉操作中，维修场所染色体与维修方式染色体均采取单点交叉法。任意选取种群中2个个体作为父代个体，对2个父代个体相同位置之后的基因进行交换，进而产生新的子代个体。

在变异操作中，维修场所染色体与维修方式染色体均采取单点变异法，当变异位置x位于维修场所染色体时，维修场所染色体的变异位置x对应的基因根据式（7）重新生成，且对应的维修方式染色体基因根据式（8）重新生成。当变异位置x位于维修方式染色体时，因受维修场所染色体的约束，变异位置对应的基因在维修方式集G中重新选择生成。

3）选择。

对满足维修优化模型约束条件的个体，根据支配概念，以秩的大小对种群快速排序，将秩为1的非支配个体留存组成精英种群。当种群迭代至规定值时输出Pareto最优集。

5 实例分析

动车组某机械系统由7个部件串联组成，各部件的参数根据文献［18-20］设定，如表2所示。

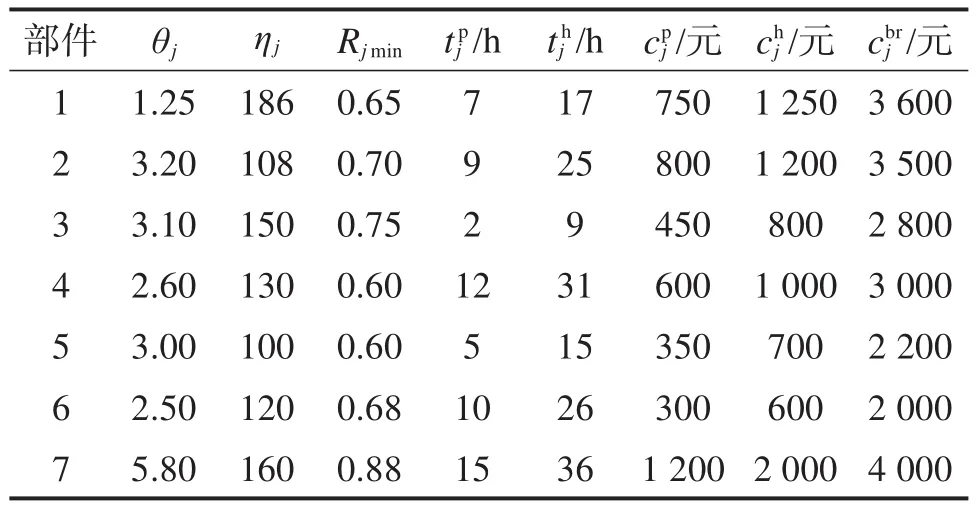
表2 动车组某机械系统各部件的参数Table 2 Parameters of each component of electric multiple unit mechanical system

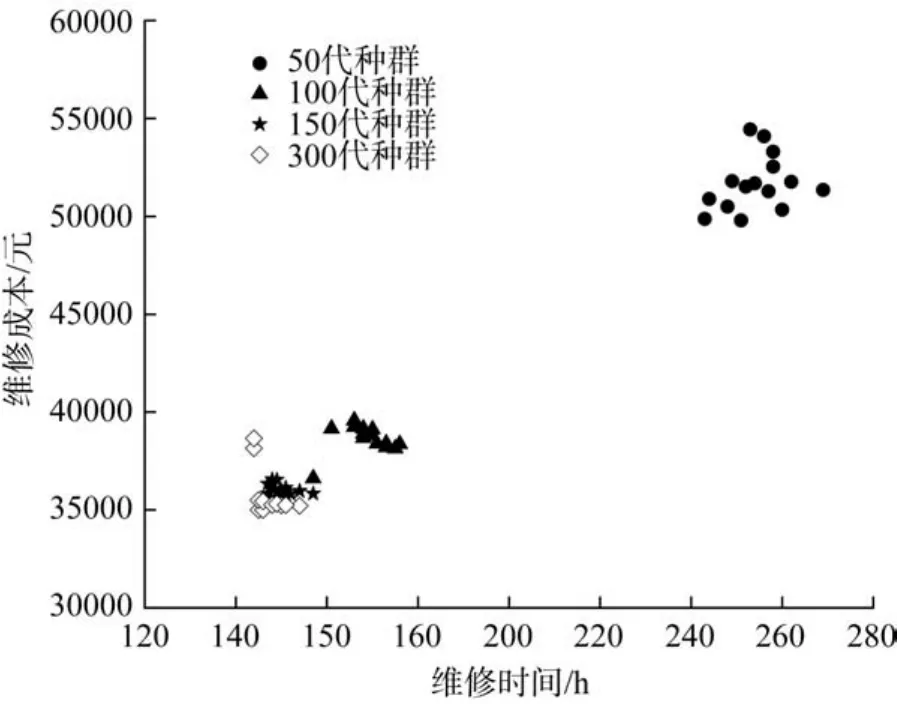
图4 不同种群代数下动车组某机械系统维修方案的优化解对比Fig.4 Comparison of maintenance scheme optimization solutions of electric multiple unit mechanical system under different population generations

为验证考虑维修场所的必要性，对2种维修方案进行对比分析。其中方案1不考虑维修场所，从部件层角度出发，对各部件的维修时机与维修方式进行优化；方案2为考虑维修场所。2种维修方案的优化结果如表3所示。

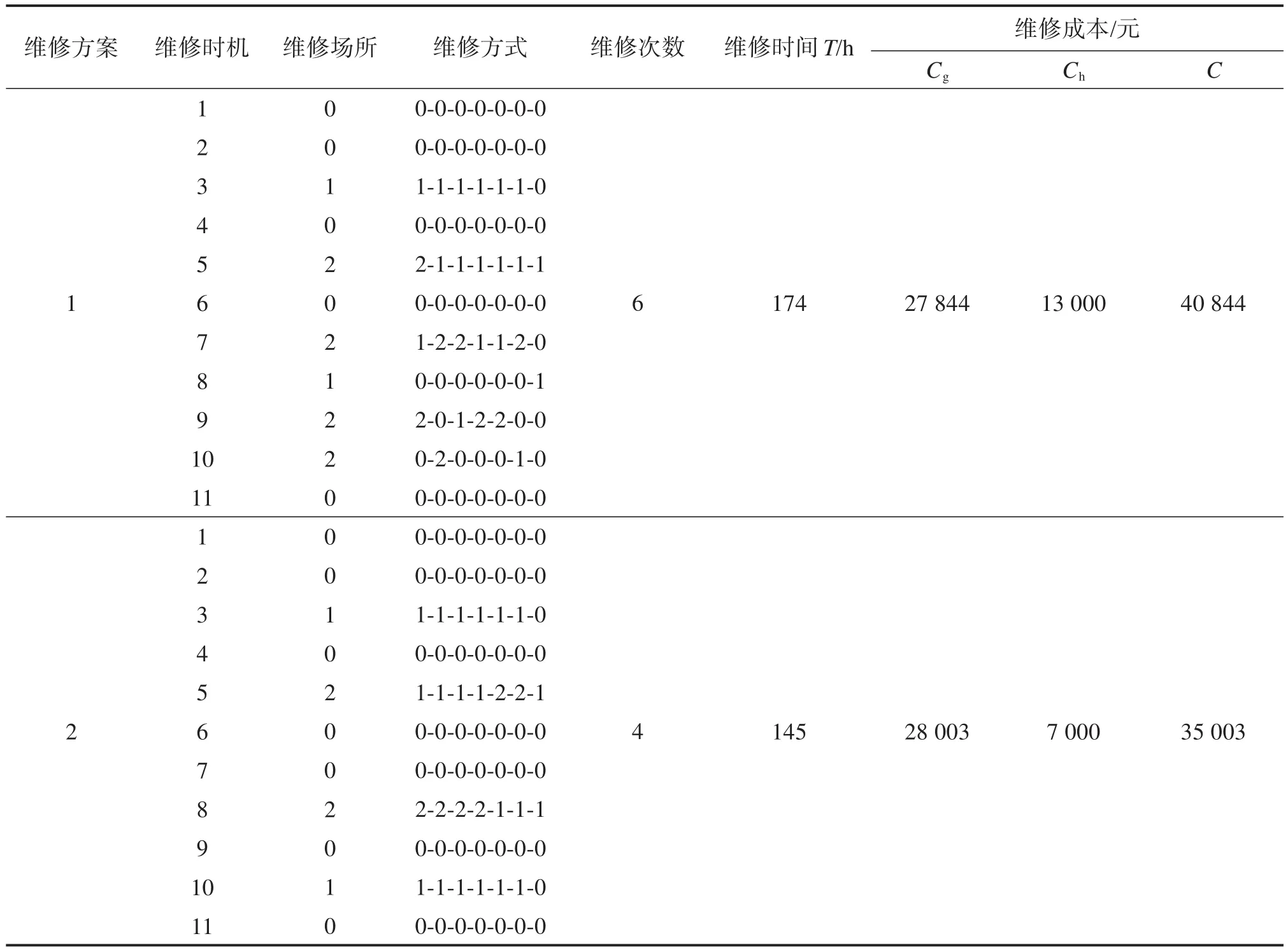
表3 动车组某机械系统不同维修方案的优化结果对比Table 3 Comparison of optimization results of different maintenance schemes for electric multiple unit mechanical system

由表3可知：相较于方案1，方案2能较好地归并部件的维修时机，减少动车组前往维修场所的次数，且方案2的维修方式较为集中，即部件的高级维修操作大多在同一维修时机进行，进而减少了动车组前往动车段维修的次数，降低了系统层维修成本。

从维修成本和维修时间的角度分析，方案2的总维修成本比方案1降低了14.3%，这主要是因为方案2的系统层维修成本优势明显，较方案1的降低了46.2%。此外，方案2的维修时间比方案1缩短了16.7%。

综上所述，考虑维修场所的方案2的维修成本和维修时间均优于方案1，验证了考虑维修场所因素制定维修策略的优越性。

表4所示为方案1和方案2中不同维修时机下该动车组机械系统的维修时间。分析表4可知，方案2中部件的维修时机较为集中，在部件维修任务分配算法下能以较短的时间完成维修任务。

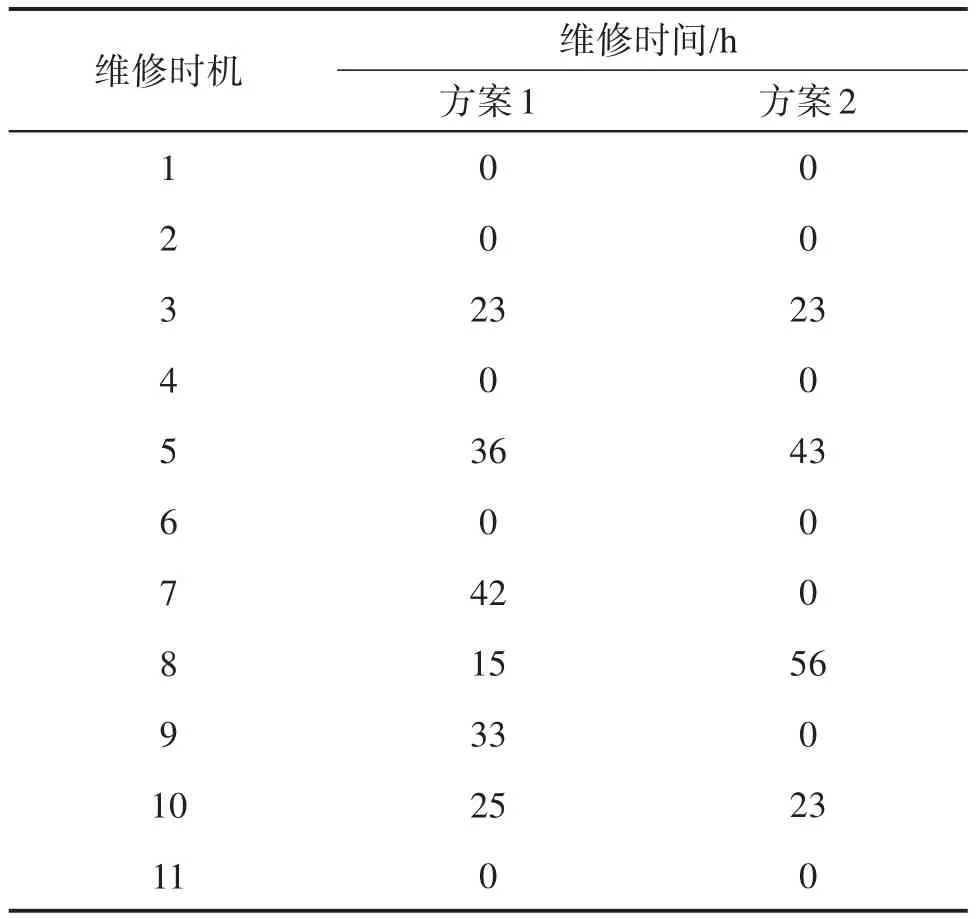
表4 基于不同方案的动车组某机械系统维修时间Table 4 Maintenance time of electric multiple unit mechanical system based on different schemes

为验证所提出的部件维修任务分配算法的有效性，以方案2中第8次维修时机为例，对待维修部件与维修人员的匹配问题进行分析。第8次维修时机下待维修部件维修时间的集合X8={17 h，25 h，9 h，31 h，5 h，10 h，15 h}。图 5 为基于本文算法的该动车组机械系统第8次维修时机的部件分配方案。通过与枚举法对比，发现基于本文算法的部件分配方案与枚举法的结果完全一致，验证了所提出算法的有效性。

6 结 论

1）考虑到维修场所对维修方式的约束作用，运用遗传算法对维修场所和维修方式进行优化选择，克服了以往动车组系统维修模型中各部件维修时机离散化与维修方式差异化的不足，从而减少了动车组系统的维修成本和维修时间。

2）提出了一种部件维修任务分配算法，实现了维修人员和部件维修任务的优化匹配，使得动车组系统维修时间最短。

3）本文以动车组系统为研究对象制定维修策略，但受研究层次的局限性，策略制定方不能从全局角度统筹规划动车组维修策略。今后应将研究对象进一步扩展至动车组车队，从车队运维的角度进行研究，使动车组维修计划更全面且可协调。