整车质量与道路坡度同步估计算法对比

王 虎, 余 强, 李学博, 王 姝

(长安大学 汽车学院,陕西 西安 710064)

在现代车辆控制中,若可以准确地实时估计整车质量和道路坡度这2个重要参数,则许多车辆控制策略能够得到改进,进而提高车辆的性能。整车质量会随乘客数量和载货质量变化,尤其是重型汽车,其质量变化能够达到400%[1],而质量的变化对许多主动安全控制系统有着重要影响。随着智能驾驶水平的不断提高,整车质量和坡度的精确辨识能有效地改善包括自适应巡航控制系统(adaptive cruise control,ACC)、自动紧急制动系统(automatic emergency braking,AEB)等先进驾驶辅助系统(advanced driving assistant system,ADAS)的性能,为驾驶员提供更加安全和方便的驾驶体验[2]。此外精确的质量和坡度对剩余续驶里程的预测、换挡质量和坡度对剩余续驶里程的预测及换挡策略的优化而言,都是必不可少的。

整车质量和道路坡度的估计方法通常分为基于传感器的方法和基于模型的方法[1]。基于传感器的方法需要在车辆上使用额外的传感器,从而估计1个或多个参数,如道路坡度可以通过倾角传感器或加速度传感器间接测量[3]；但这些方法所需要的设备比较昂贵,不适合量产车使用,因此基于模型的方法受到了更多的关注。基于模型的方法利用车辆纵向动力学模型和通过控制器局域网络(controller area network,CAN)获取相关数据,如发动机扭矩、转速、车辆速度和变速器传动比等,建立状态方程,并采用各种算法对整车质量和道路坡度参数进行估计。

目前,在整车质量和道路坡度估计方面,国内外学者已经提出了多种方法,大体可以分为以下2类。

(1) 同步估计方法,即同时估计这2个参数。文献[4]提出了基于稳态卡尔曼滤波的车辆质量与道路坡度估计;文献[5]提出了基于扩展卡尔曼滤波(extended Kalman filter,EKF)的车辆质量与道路坡度估计;文献[6]提出了基于多遗忘因子最小二乘法的整车质量和道路坡度同时估计方法;文献[7]采用前馈神经网络(feedforward neural network, FFNN)对整车质量和道路坡度进行估计。

(2) 分步估计方法。文献[8]建立双层估计器结构对整车质量和道路坡度进行估计,第1层对整车质量、轮胎惯性矩和平路坡度等慢变参数进行估计,第2层将第1层的估计量作为已知参数对不平路面的坡度等快变参数进行实时估计;文献[9]提出了用于估计整车质量和道路坡度的自适应分级(two-stage)估计器,第1阶段利用自适应参数估计器得到整车质量,并作为第2阶段自适应非线性快变系统估计器的常数输入对道路坡度进行估计;文献[10]提出了一种适用于商用车质量估计的双层结构估计器,第1层基于加速度传感器信号采用最小二乘法对坡度进行估计,其中考虑了商用车悬架变形对其估计值的影响，第2层将第1层估计得到的坡度值作为观测量之一,采用EKF对整车质量和坡度进行估计。

对于双遗忘因子递归最小二乘法(recursive least square with multiple forgetting factors,RLS-MFF)、EKF和无迹卡尔曼滤波(unscented Kalman filter,UKF)3种常见的算法,在整车质量和道路坡度这2个变化速率不同的参数估计中,RLS-MFF采用2个遗忘因子淡化2个参数的历史数据对估计结果的影响[11],通过递推关系得到下一时刻的估计值;而2种滤波算法采用状态方程,通过上一时刻状态变量的估计值和当前状态变量的测量值得到当前状态变量的估计值[5],估计过程中EKF需要对非线性系统进行线性化,而UKF通过无迹变换(unscented transform,UT)避免了这个步骤。RLS-MFF中遗忘因子的取值直接影响估计效果的好坏,EKF中线性化会引起误差,而UKF没有以上问题,属于精度相对较高的算法。

本文通过车辆纵向动力学模型,设计基于UKF的整车质量和道路坡度联合估计器,并通过CarSim中建立的车辆、道路模型得到试验数据传输至MATLAB,并将得到的离线估计结果与RLS-MFF和EKF算法的估计结果进行对比。

1 车辆纵向动力学模型

汽车加速上坡行驶过程中的受力情况分析如图1所示。

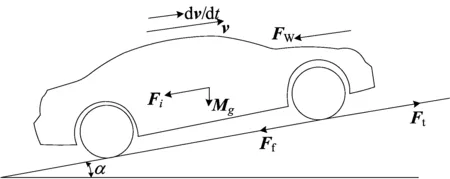
图1 汽车加速上坡受力分析

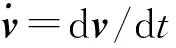
(1)

根据汽车理论中相关公式,车辆的纵向动力学方程可写为:

(2)

其中:Ttq为发动机转矩;ig为变速器的传动比;i0为主减速器的传动比;ηT为传动系的机械效率;r为车轮半径;g为重力加速度;f为滚动阻力系数;α为坡道角;CD为空气阻力系数;A为迎风面积;ρ为空气密度;v为行驶速度[11]。

根据我国公路路线设计规范,一般道路的坡度均较小[12],此时sinα≈tanα=i,cosα≈1,故(2)式可写为:

(3)

其中,i为道路坡度。

2 UKF算法

2.1 UKF算法

卡尔曼滤波器用反馈控制的方法估计过程状态，即滤波算法估计过程中某一时刻的状态,然后以(含噪声的)测量变量的方式获得反馈[4]。在几何上,卡尔曼滤波器可以看作状态变量在由观测生成的线性空间上的射影,因此对于非线性系统滤波问题,卡尔曼滤波不再适用。常用的EKF是利用线性化技巧将非线性系统滤波问题转化为近似的线性滤波问题,一般围绕滤波值将非线性函数通过泰勒展开并保留一阶近似项得到,但此过程必定会引入线性化误差,且线性化假设不成立时可能会造成滤波器发散。UKF采用卡尔曼线性滤波框架,对于一步预测方程,使用UT来处理均值和协方差的非线性传递问题。UKF是对函数的概率密度分布进行近似,从而逼近状态的后验概率密度,没有忽略高阶项,因此对于非线性分布的统计量有较高的计算精度,克服了前2种滤波的缺陷[13],而相对于RLS-MFF,UKF只用到上一时刻的状态而不需要之前所有的状态,不用淡化历史数据的影响。

2.2 UKF算法实现

非线性系统的状态估计模型可以通过状态空间方程的形式来表示,包括状态方程和观测方程,其离散化后的方程形式为:

(4)

其中:f为非线性状态方程函数;h为非线性观测方程函数;xk为k时刻的状态向量;zk为k时刻的观测向量;uk为k时刻的输入向量;Wk、Vk分别为过程噪声向量和观测噪声向量。

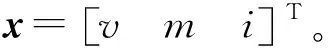
(5)

观测方程为:

(6)

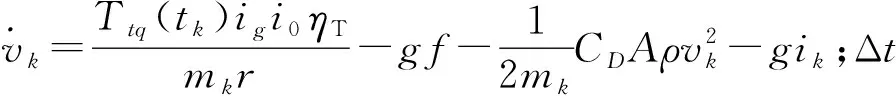
设Wk具有协方差矩阵Q,Vk具有协方差R。UKF算法的流程[14]如图2所示。

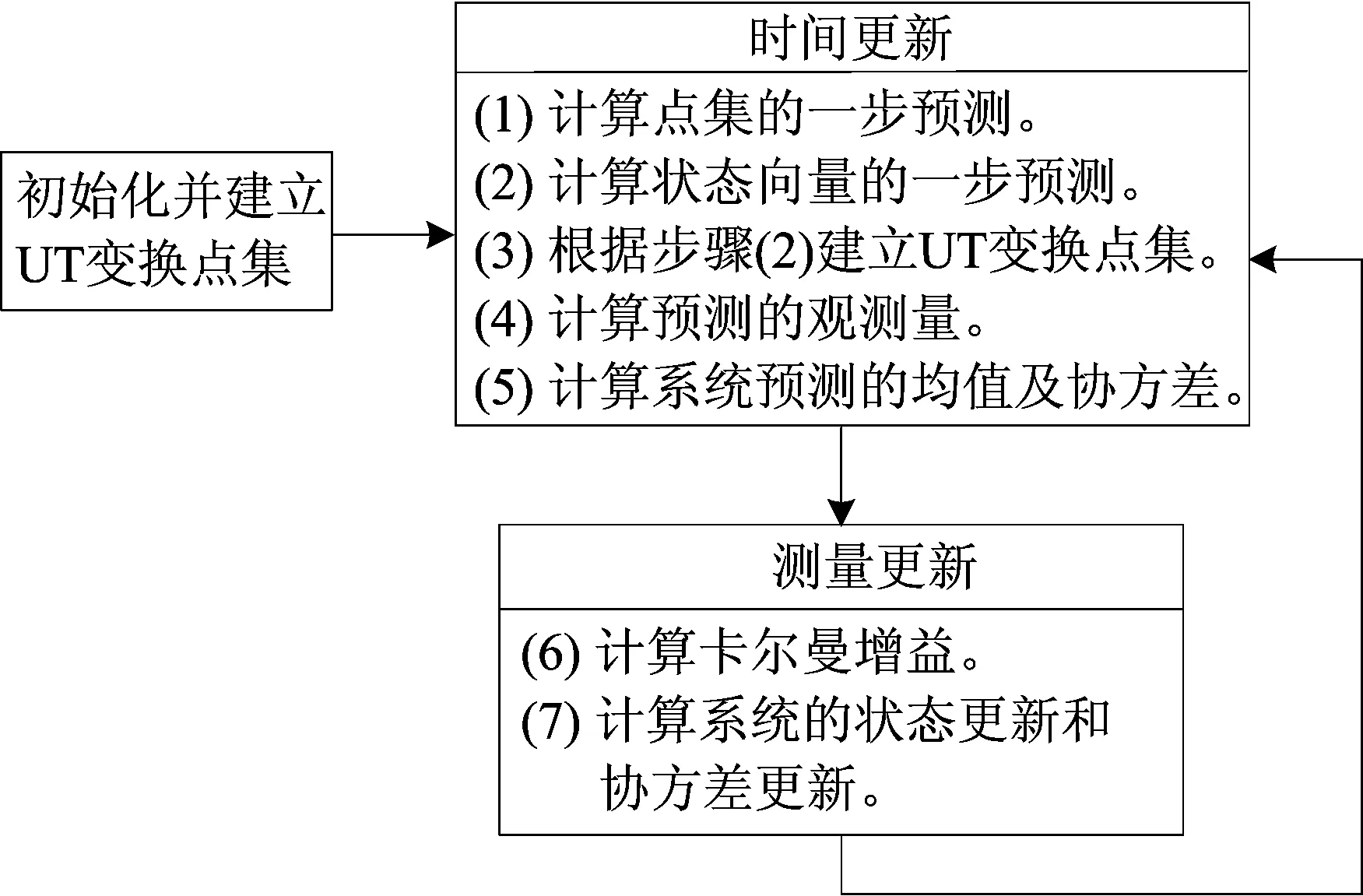
图2 UKF算法流程

UT变换方程为:

(1) 计算2n+1个Sigma点。计算公式为：

(7)

(2) 计算这些采样点相应的权值。计算公式为：

(8)

其中:下标m表示均值;下标c表示协方差;n=3;λ=a2(n+κ)-n，a的选取控制了Sigma点的分布状态,通常选取较小的正值10-4≤a≤1,本文取a=0.01，κ为待选参数,通常n+κ=3;β为一个非负的权系数,它可以合并高阶项的动差,对于服从高斯分布的状态变量,β=2是最优的[13]。

时间更新方程为:

(9)

(10)

(11)

(12)

(13)

(14)

(15)

测量更新方程为：

(16)

(17)

(18)

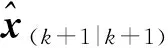
3 仿真实验

采用计算机虚拟仿真试验对3种同步估计算法性能进行对比。在CarSim中建立车辆、道路模型并完成车辆模拟仿真试验,通过接口将包括车速、发动机转矩、变速器挡位、实时坡度在内的数据传输至MATLAB。同时,为了反映更加真实的估计效果,参考CAN总线数据采集的实际情况,在MATLAB环境中对车速与发动机转矩数据分别加入高斯白噪声,最终完成实时估计,仿真原理图如图3所示。

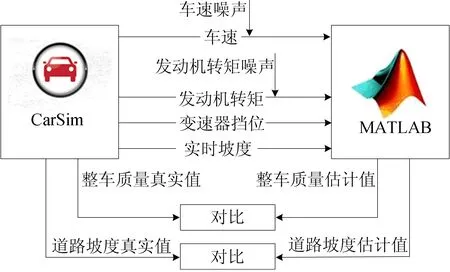
图3 仿真原理图

其余车辆模型中的参数均视为已知参数,具体见表1所列。

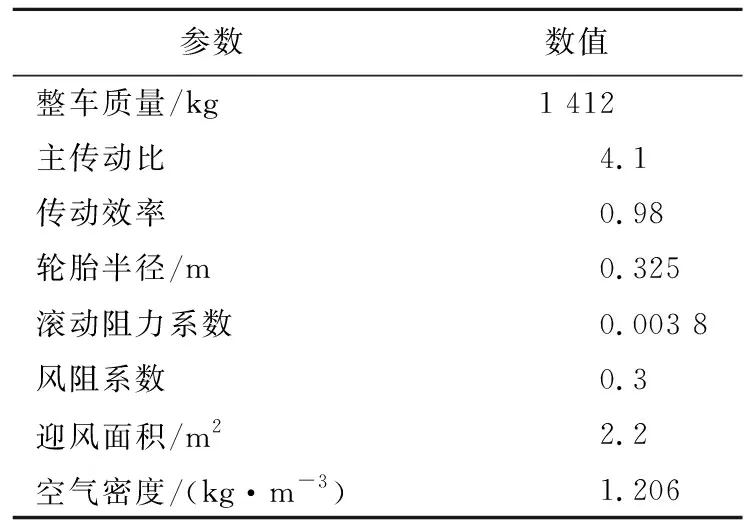
表1 车辆参数

为了验证在不同道路状况下估计算法的性能,在CarSim中分别构建定坡度道路与变坡度道路,在2种道路条件下进行3种估计算法的对比分析。

车辆由车速为0开始以固定节气门开度(0.13)加速,期间未进行换挡与制动操作。

在RLS中,整车质量与道路坡度所对应的遗忘因子λ1、λ2分别设为1和0.6。在EKF和UKF中,过程噪声协方差矩阵Q设为diag[10-41 10-4],测量噪声协方差R设为0.1。

3.1 定坡度道路

定坡度道路由一段平路与一段固定坡度(约5.7°)的上坡路组成,两者之间通过缓变坡度平滑过渡。仿真时长为30 s,数据采样频率为10 Hz。仿真模拟得到的车速和发动机转矩如图4所示。

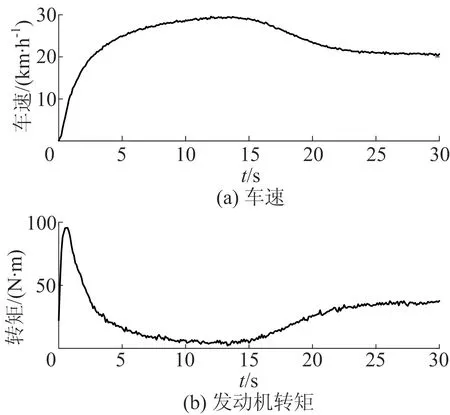
图4 定坡度道路试验结果

3种同步估计算法在定坡度道路下的整车质量与道路坡度估计结果及误差如图5所示。从图5可以看出,RLS-MFF、EKF和UKF算法对整车质量与道路坡度的估计结果与真实值都较为一致。对于EKF和UKF算法,道路坡度值会在估计初期出现较大的波动,这是由整车质量的预设初始值与真实值存在一定的偏差所导致,随着质量收敛到真实值(约2 s时),道路坡度估计误差也逐渐变小趋于稳定;当坡度发生变化时,EKF和UFK的坡度估计值存在一定的迟滞,而RLS-MFF算法的估计结果始终与真实值偏差较小。3种算法对于整车质量的估计都有一定误差,其中EKF算法表现最好,RLS-MFF算法表现较差。

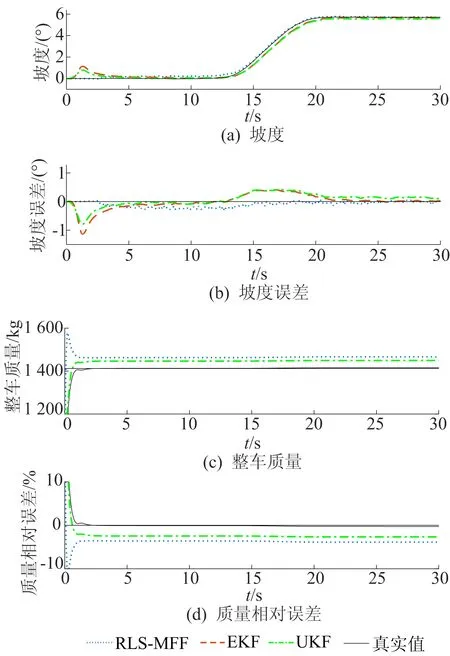
图5 定坡度道路估计结果及误差对比

3.2 变坡度道路

变坡度道路中,坡度由0°开始进行无规则地连续变化,最大坡度达到约10°,仿真过程中的车速与发动机转矩如图6所示。

3种同步估计算法在变坡度道路下的整车质量与道路坡度估计结果及误差如图7所示。从图7可以看出,RLS-MFF、EKF和UKF算法对整车质量与道路坡度的估计结果都存在较小的误差。在连续的坡度变化中道路坡度估计的误差会出现上下波动,且随着算法的运行误差逐渐减小,其中UKF算法表现介于RLS-MFF和EKF算法之间。对于整车质量的估计UKF算法相较于定坡度道路表现更好,更加逼近真实值。

图6 变坡度道路试验结果

图7 变坡度道路估计结果及误差对比

3.3 估计精度与实时性分析

为了更加直观地对比3种估计算法在整车质量和道路估计方面的性能,从估计精度和实时性2个角度进行定量分析。选择均方根误差(root mean square error,RMSE)与平均绝对误差(mean absolute error,MAE)作为估计精度的量化分析指标,其计算公式分别为:

(19)

(20)

选择单次迭代时间作为算法实时性的量化分析指标,即每进行一次迭代计算得到当前这一时刻估计值所用时间的平均值。本文将每种算法分别运算10次取平均值,作为最终评价指标。所用计算机CPU型号为Intel Core i5-3230M(主频为2.60 GHz),运行内存为6 GiB,运算环境为MATLAB R2016a。

3种算法在变坡度道路上的估计误差和运算时间统计见表2所列。算法精度方面,3种算法均存在较小的误差,RLS-MFF算法所估计的坡度误差最小,质量误差最大,小于5%;UKF的质量估计误差与EKF相差甚小,但坡度估计的精度明显优于EKF。实时性方面,RLS-MFF的运算时间最短,UKF运时间最长,单次迭代时间为1.223 6×10-4s,满足估计算法的实时性要求。

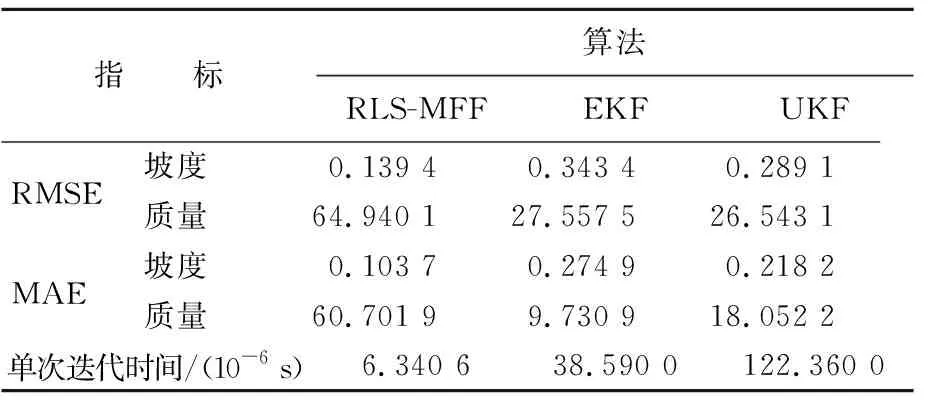
表2 估计误差和运算时间

4 结 论

(1) 本文提出了基于UKF整车质量与道路坡度的估计算法,以车辆纵向动力学模型为基础,推导系统的状态方程和观测方程,并给出UKF算法的流程图及相应的公式。

(2) 利用CarSim/Simulink联合搭建的仿真平台比较了3种算法的估计效果,并利用RMSE与MAE评价算法的计算精度,利用单次迭代时间评价算法的实时性。结果表明UKF算法在估计精度方面表现良好,实时性较差,但能够满足算法的实时性要求,其估计结果可用于进一步的车辆控制当中。