《笔算乘法（不进位）》教学设计

2022-05-06汪慰生

小学教学设计(数学) 2022年4期

文|汪慰生

【教学内容】

人教版三年级上册第60页。

【课前思考】

以教材、学情的分析为导向，帮助学生建构数学模型为基准，我对本课的教学设计有三点思考：一是学生已有知识经验丰富，是否可以去情境化，从数学本源探究乘法竖式计算？二是在前测中，有的学生根据加法竖式来列乘法竖式计算，是否可以通过加法竖式与乘法竖式的直观比较，制造认知冲突，从本质上加强学生对乘法竖式计算的认知清晰度？三是数小棒、画图、加法计算等方法处在辅助理解的位置，是提倡算法多样化，再来学习乘法竖式计算，还是先让学生直接尝试乘法竖式计算，再有选择地利用上述的辅助方法帮助理解？

基于以上思考，我对教材编排有两点较大的改动：一是将北师大版的点子图改为摆小棒，我认为摆小棒对于12的组成是更直观的表示，一个12是一捆小棒（10）和2根小棒，更为有效体现12×3是由3个2和3个10相加而来；二是导入环节我在口算乘法的基础上去情境化，学生对于乘法的意义在口算乘法这节课上已经有了一定的认知经验，并且学生对于列乘法竖式是有一定的提前接触，并不完全是一张白纸。直接从加法竖式和乘法竖式的迁移冲突中直奔本课乘法竖式计算的意义和算理，在比较中认知、感悟，让学生对加法竖式和乘法竖式模型有更清晰的认识和辨析。生活创造了数学，数学就应回到生活中、运用到生活中，所以我在后续环节还为学生提供了数学联系生活的时间与空间。

因此，我融合北师大版、人教版、浙教版教材，创新性地使用教材设计教学，并付诸教学实践，对《笔算乘法（不进位）》一课进行研究。

【教学目标】

1.体会多位数乘一位数笔算乘法的意义，理解乘法竖式的算理，掌握算法。

2.在学生自主探索和说理交流的过程中，建构乘法竖式计算的模型。

3.体会数学与生活之间的联系，感悟数学学习的阶梯性与必要性，激发学生的探究兴趣。

【教学重、难点】

理解笔算乘法的算理，建构数学模型。

【教学准备】

课件、磁性小棒。

【教学过程】

一、十位上的1为什么要乘3

师：同学们，我们学过加法竖式计算，12+3会算吗？

（课件出示12+3的竖式计算）

生：等于15。

师：今天，我们要学笔算乘法，12×3你会列竖式计算吗？

（课件出示12×3的竖式计算）

师：拿出练习本，试试看！

（学生独自尝试列乘法竖式计算，教师巡视，查看学生完成情况）

师：同学们，大家列乘法竖式计算的方式有这两种。

（大部分学生都是第二种算法）

师：12×3等于16还是36？

生：等于36，16是错的。

师：（看着第一种算法的学生）他说你做错了，做这道题时，你是怎么想的？

生：我是先算二三得六，再把1写下来。

师：是啊，刚才我们算加法也是这么算的，先算个位，2+3等于5，再把十位上的1照写下来，乘法不也是一样吗？

生：不一样，1还要乘3。

师：他说十位上的1要乘3，你有什么想问他的吗？

生：1为什么要乘3？

师：是啊，为什么十位上的1要乘3呢？

生：因为有十位所以要乘。

生：因为它是乘法，所以3要乘十位上的1。

生：因为整个12都要乘3。

师：加法中的整个12加3和乘法中的整个12乘3，它们有什么不一样？也就是说12×3表示的是什么？

生：3个12相加。

师：能用小棒来摆一摆吗？你能说一说为什么这么摆吗？

（学生边说，教师在旁边列出加法竖式）

师：加法是怎么算的？先算3个2相加，再算——

生：3个10相加。

师：知道为什么1要乘3了吗？

师：是的，12×3表示的是3个12相加，所以不仅要算3个2相加，也要算3个10相加。

【设计意图：原教材的处理是从学生的已有经验出发，通过加法、口算、点子图等，帮助学生理解掌握乘法竖式计算的算理和算法。但是前测结果告诉我们，大部分学生都是会乘法竖式计算的，但有一部分学生对于乘法竖式计算的认知并不是建立在理解的基础上。因此，本环节先让学生直接尝试乘法竖式计算，制造加法竖式和乘法竖式之间的认知冲突，以“十位上1为什么要乘3”为问题导向，有需要的前提下，借助数小棒、加法竖式等已有知识经验辅助思考，引导学生在对加法与乘法意义的探究讲理过程中进入知识深处，对乘法有更深层次的认识。】

二、36是怎么得来的

师：老师的外甥也是列乘法竖式计算，但是和你们列的不一样，他算出来也等于36，这种方法大家认同吗？

（有少部分学生认同）

师：你认为是对的，你是怎么想的？

生：首先2和3相乘等于6，然后10乘3等于30，两个加起来等于36。

师：谁听明白了？

生：他第一步先算2×3，第二步再算10×3，最后得数加起来。

师：能在小棒图上圈一圈吗？

（学生上台圈出6和30分别在小棒图上的部分）

生：6是3个2相加，30是3个10相加。

师：看明白计算过程了吗？谁能再结合加法竖式计算说一说？

师：看来我外甥的算法是正确的，这么说你们做的就是错的？

生：一道题不可能只有一个答案。

师：他说的答案是计算结果吗？那是什么意思？

生：算法有很多种，答案只有一个。

师：你说的答案是这个意思吗？能说清楚了吗？

生：两种方法都是对的，计算的方法可以有很多种。

师：你们是怎么算的呢？

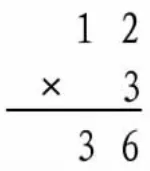
师：他算了几步？

生：两步。

师：两步？我没看出来，谁来说说？

生：第一步算2×3=6，第二步算10×3=30，相加等于36。

师：30里的0跑哪里去了？

生：6和30相加等于36，0就省略了。

师：是的，两种方法都是一样的，都算了两步，只是为了简便，习惯上采用你们这种方法。

【设计意图：本环节围绕“36是怎么得来的”问题展开学习，引导学生观察、比较、辨析、表达，在已有经验基础上，借助数形结合等方式交流想法，在对两种竖式计算步骤的探讨过程中，梳理乘法竖式计算的算理，建构起清晰的乘法竖式模型，完善认知结构，从而知算理、明算理。】

三、算法的感悟、总结

师：今天学习了笔算乘法，我们不仅列出乘法竖式计算，还用了数小棒、加法竖式计算的方法，请同学们比较一下，这些方法有什么相同点？

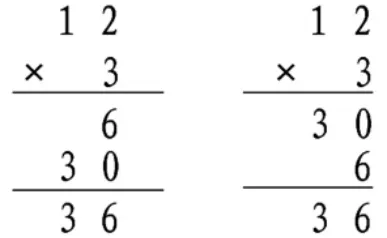
生：有的是先算2×3，再算10×3；有的是先算10×3，再算2×3；最后再相加。

师：第一种算法中，2×3、10×3各表示什么？36表示什么？

生：3个2相加，3个10相加，36是两部分相加的得数。

师：第二种算法中，10×3、2×3又各表示什么？36呢？

生：3个10相加和3个2相加，36也是两部分相加的得数。

师：发现了吗？这些方法虽然不一样，但都是先把3分别和每一位上的数相乘，再把分开乘后的两个得数加起来，这就是它们的相同点。

师：同学们，学数学就是要在生活中运用，你能根据12×3编一个生活中的数学问题吗？

生：妈妈买了12颗糖果，爸爸和姐姐又各买了12颗糖果，一共买了多少颗糖果？

生：我一天种12棵树，种了3天，一共种了几棵树？

生：我今天买了3个文具盒，一个文具盒12元，一共多少元？

……

师：有关12×3的问题说得完吗？是的，生活中处处都有数学！

【设计意图：本环节意在突出两点：第一，沟通各种算法之间的联系，建立乘法与加法之间的纽带，引导学生归纳各种算法的算理，明白算法不一样、算理却一样的数学道理，感悟数学思想；第二，加强数学与生活之间的联系，积累基本的数学生活经验以及启发学生运用数学知识解决生活问题，让数学回归生活。】

四、巩固反馈

师：大家都会列乘法竖式计算，现在能说清计算道理了吗？完成这两道题，并和同桌说一说。

课件出示练习一：

（学生独立完成后同桌交流）

师：如果是三位数乘一位数的竖式计算，你们会吗？试试看。

课件出示练习二：

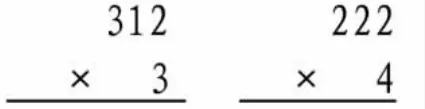
师：三位数乘一位数，你们学过吗？没学过怎么会呢？你们是怎么想的？

生：与刚才两位数乘一位数是一样的道理，先算2×3，再算10×3，然后算300×3，最后加起来。

生：第二题就是2×4、2×4、2×4，然后相加。

师：你们听明白了吗？

生：第二题应该是这么算的，先算4个2，再算4个20，接着算4个200，最后相加，计算道理都是相同的。

师：是的，看来把算理说清楚很重要！那么，如果是四位数乘一位数？五位数乘一位数？甚至是多位数乘一位数呢？

生：计算道理也是一样的。

师：是的，它们的计算道理都是一样的，都是在算有几个几相加。

课件出示练习三：

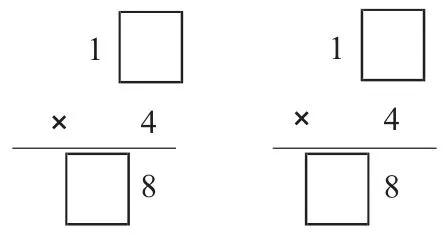
师：方框里要填几？你是怎么知道的？

师：当遇到要进位的情况，你们是选择从个位算起还是从高位算起呢？大家回去可以思考一下，我们在下一节课《有进位的笔算乘法》中展开研究！

【设计意图：本环节通过练习检验学生对乘法算理的认知程度，三位数乘一位数的竖式计算是对学生知识迁移能力的考验，利用已有经验解决类似的数学问题；222×4是对乘法算理的最终梳理，明白讲清计算道理的重要性；练习三的设置是为下节课《进位的笔算乘法》做铺垫，让学生对乘法竖式计算从个位算起的简便留下思考；另外，在前面环节为给学生留足思考、说理的时间和空间，练习量相对进行了减少。】