直尺衍射现象及分析

姜向前，王 莹，宋 扬，赵春宇，张 宇

(哈尔滨工业大学 物理学院，黑龙江 哈尔滨 150001)

光波遇到障碍物时发生偏离直线传播的现象称为光的衍射，是光波动性的一个重要特征.衍射现象具有两个鲜明的特点，即限制与扩展[1]，只要光在波前传播方向受到限制则产生衍射，那么远处屏上的衍射光强就沿该方向扩展开来.障碍物的尺度与波长之间的关系决定了衍射现象的强弱.只要障碍物的尺寸在λ～103λ之间就会得到明显衍射现象.

由于衍射结构与衍射图样是一一对应的，因此可利用衍射图样进行结构分析、形貌表征.大学物理实验中利用衍射进行测量的简单例子是光栅衍射测光栅常数和波长[2,3].激光入射光栅，由衍射光斑即可实现对波长的测量.直尺刻线亦可认为是光栅结构，利用直尺衍射也可实现对光波长的测定.但在测量过程中发现一个有趣的现象，当入射光斑照射到直尺边缘或钢尺表面非刻度区时衍射屏上出现半圆形衍射光斑.由于衍射光斑与衍射结构一一对应，本文将理论结合实验针对直尺的衍射现象开展研究.

1 直尺衍射图样及其表面形貌

无论对于塑料尺还是钢尺，如图1(a)所示，不论入射光照射刻度线侧边缘还是照射非刻度线边缘都会出现如图1(c)所示的衍射图样.若将激光束入射直尺表面空白区域如图1(b)所示，对于塑料尺与亚光钢尺衍射屏上只有反射光斑，无半圆形衍射光斑出现.对于抛光钢尺，衍射光斑沿x方向向两侧扩展，有半圆形衍射图样出现如图1(d)所示.由此可判断，对于塑料尺与亚光钢尺表面无规则结构, 而对于抛光直尺表面应该存在规则结构.无论入射钢尺表面与边缘都会有半圆形衍射图样出现意味着表面与侧面具有类似的微观结构.为了证实这种判断，将利用光学显微镜对直尺表面与侧面进行表征, 如图2所示.

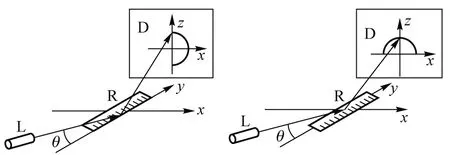
直尺边缘衍射 直尺表面衍射

抛光钢尺表面成像 亚光钢尺表面成像

由表征结果可知，塑料直尺与亚光钢尺表面并无规则结构，因此只在反射点处得到一个亮斑，光斑并未发生扩展.塑料直尺侧面与抛光钢尺表面、侧面发现复杂条形结构.尽管出现规则的条形结构却并不能得到明确的周期，但可认为是多套条形光栅的叠加.虽然由表征结果得到了规则的衍射结构，但这种条形结构的衍射图样为什么是半圆形仍不得而知，为了解释半圆形衍射光斑，下面我们将从简单的二值光栅的衍射理论出发给出结果分析.

2 直尺衍射图样理论分析

为了解释直尺侧面与抛光钢尺表面的半圆形衍射图样，考虑最简单的情况，即二值光栅的衍射.文献中已有很多二值光栅的衍射行为的讨论[4-8]，Harvey和Vernold[5]利用方向余弦解决了二值光栅的圆锥衍射问题.基于圆锥衍射我们将讨论存在微结构的直尺表面的衍射问题.

首先考虑一束光入射标准光栅如图3所示，θi为入射角，φ0和φ为方位角，θ0为极角.光栅矢量G平行于α轴，而光栅槽沿β轴，直角坐标系中r(x,y,z)在方向余弦空间中的3个分量为

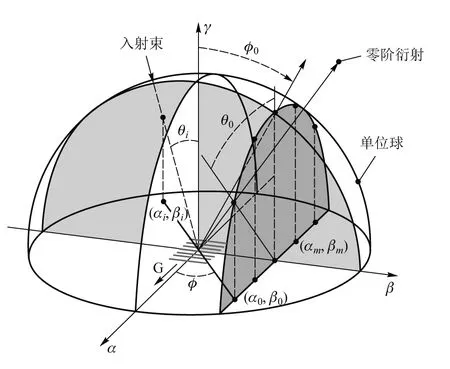
图3 方向余弦空间中反射光栅的圆锥衍射

(1)

α,β,γ满足α2+β2+γ2=1.

入射光与单位球面的交点在αβ平面上的投影为(αi,βi)，由图可知

(2)

整理得

(3)

由图3可知β轴方向波矢分量为βm=ky/k0=sinθisinφ，由于入射角θi与方位角φ是确定的值，则β方向波矢分量为定值，即所有衍射级次位于同一个垂直β轴的平面上，进而可得βm+βi=0.由式(3)可得

βm=-sinφ0

(4)

(5)

由式(5)可知αm、γm在半径为|cosφ0|的圆周上.下面我们进一步讨论各衍射级次的间距问题.由光栅方程αm+αi=mλ/d(m为整数，d为光栅周期)[6]可得

(6)

由式(6)可得

(7)

由式(5)和式(7)可知，所有衍射级次等间距分布在同一圆上.下面给出衍射光斑的尺寸，假定光栅距衍射屏距离为L，考虑特殊情况即入射面为βγ平面，入射角为θi，则有tanθi=L/r，其中r为衍射屏上对应圆衍射光斑的半径，整理得

(8)

至此，我们已经推导了光入射条形光栅各衍射阶次的分布规律，发现对于标准二值光栅各衍射级次离散分布在一个与栅屏距L、入射角θi相关的一个圆上.若入射反射光栅，衍射光斑为半圆；若入射透射光栅，衍射光斑离散分布在整圆上.由二值光栅衍射结果可知，对于存在条形结构分布的直尺侧面与表面，均可看成是多套光栅的叠加，叠加的结果导致衍射光斑不再离散分布，而是连续分布形成一个圆.

为了验证式(8)，表1给出了两个入射角下衍射光斑半径r与衍射屏距离为L的关系.由式(8)可得到衍射角分别为34.7°和65.2°.由表1可看出当改变不同的衍射距离L时，半圆形衍射光斑的半径随之改变，二者满足式(8).

表1 衍射光斑半径与入射角的关系

3 结论

本文理论结合实验解释了直尺表面、边缘的衍射问题，研究发现直尺侧面与抛光钢尺表面的衍射光斑呈半圆形.光学显微镜观察直尺侧面与钢尺表面存在类光栅结构.基于二值光栅衍射理论，给出了圆形衍射光斑的定性解释.直尺表面的类光栅结构可看作是多套二值光栅的叠加，光栅衍射的叠加导致了半圆形衍射光斑的出现.另外，对于标准的光栅，衍射光斑并不存在展宽.但直尺表面不同周期的光栅的槽深是不同的.与深槽和浅槽对应的零级衍射斑在衍射屏上的高度不同，因此深浅不一的光栅的衍射导致了衍射光斑在Z方向出现一定程度展宽.