肥皂膜过滤器的性能探究

马舟阳，关 舟，赵述敏，方爱平,,4，赵 迪,,4

(1.西安交通大学 物理学院，陕西 西安 710049；2.西安交通大学电气学院，陕西 西安 710049；3.西安交通大学 物理学院 物质非平衡合成与调控教育部重点实验室，陕西 西安 710049；4.西安交通大学 物理学院陕西省量子信息与光电量子器件重点实验室，陕西 西安 710049)

近几个世纪以来，针对不同物质的分离一直是一个很重要的研究和应用方向.近年来物质分离在很多方面都有重要的应用，比如废水处理、海水淡化[1].物质分离中最常用的工具就是“选择性透过膜”，它表现为能让具有一些特性的物质穿过而让具有相反或其他特性的物质停留在膜上.针对粒子体积进行分离的过滤膜是最常见、最简单的一种分离技术.传统的过滤膜是多孔的，允许比孔径小的颗粒通过，但比孔径大的颗粒会保留并停留在膜上.然而，允许大颗粒通过而保留小颗粒的薄膜很难人工制造，却常见于自然界中.例如，细胞膜是一种由磷脂双分子层为基本骨架构成的膜，它可以通过胞吞和胞吐等形式让大分子透过.这种膜必须是动态的、自愈合的才能够长期稳定的存在.这种特性在液体中十分常见，然而这种动态自愈合的过滤膜很难人工制造.受到液体自愈功能和细胞膜内吞作用的启发，Birgitt Boschitsch Stogin、Luke Gockowski等人[2]证明了完全由液体组成的液膜可以被设计成保留小于临界尺寸粒子而透过大尺寸粒子的过滤膜.

本文基于液膜的悬链曲面模型解析讨论了液膜临界透过条件，在实验上通过调整由纯液体(肥皂液)组成的液膜的浓度、成分等参量改变液膜的表面张力系数，实现了一种保留小于临界透过半径的粒子而透过大于临界透过半径粒子的选择性透过膜，验证了液膜临界透过条件，并实现了对同种粒子速度的筛选功能.这种液膜可以实现传统过滤膜无法实现的粒子分离机制，这对未来新型液膜过滤技术的研制和开发具有启发意义.

1 理论分析

为分析方便，我们假设：粒子为球形；当没有粒子穿透液膜/停留在液膜上时，液膜为无厚度的圆平面；当粒子停留在液膜上，液膜被拉伸为两个高度不同的同心圆构成的曲面.在无外力影响下，液膜有收缩至最小面积的趋势.由三维空间的极小曲面定理可知，2个高度不同的同心圆构成的极小曲面为悬链曲面.即，液膜只能以平面或悬链曲面的结构存在才能保持稳定.因此，对粒子穿透液膜过程的讨论可简化为对小球停留使液膜形成悬链曲面过程的分析.

1.1 悬链曲面方程推导

我们引入Young-Laplace方程[3]推导液膜的悬链曲面模型.通过液面附加压力、表面张力系数及曲率半径之间的关系计算液面方程，得到Young-Laplace方程：

(1)

其中R1、R2为界面主曲率，γ为液膜表面张力系数.由式(1)可得，小球停留在液膜上时液膜形状的具体形式为[3]

(2)

对式(2)进行两次积分即可求得悬链方程：

(3)

至此，我们得到了液膜稳定时的悬链曲面模型.其中C1和C2为液膜具体的形状参量.

1.2 小球临界透过条件分析

实验中，我们从液膜上方不同高度处释放小球使其下落，通过重力势能转化为动能对实现小球穿过液膜的速度控制.小球在打入液膜前的动能Ek来源于小球从高处自由下落的重力势能：

(4)

其中ρb、Rb分别为小球密度和半径，H为小球初始高度，Ef为小球下落过程中与空气摩擦造成的能量损失.小球下落过程中空气阻力正比于速度的平方，即

(5)

其中阻力系数k取0.3，在我们后续的实验中，小球半径取0.2 cm.在我们的实验条件下，即小球短距离自由下落，小球速度只能达到约0.1 m/s.在这种情况下，小球下落所受的摩擦力约为

Ff=3.76×18-8N

实验中小球的质量为0.1 g.因此，空气阻力远小于粒子自身的重力，在后续讨论中可忽略不计.

在小球打入液膜过程中，小球会受到液膜的“阻碍”作用，而液膜同样会受到小球的“拉伸”作用.基于能量守恒，小球初打入液膜时的能量全部转化为“试图穿透液膜”这一过程中产生的摩擦损耗和最终液膜表面能的增加.

首先，我们计算液膜表面能的增量.由上节可知，小球在穿透膜这一过程中液膜始终保持悬链曲面.二维截面中，设小球质心到液膜交点的连线与竖直方向夹角为α，如图1所示.在小球穿透液膜过程中，随着小球不断拉伸液膜，液膜的表面张力逐渐增加，并始终沿液膜与小球交点处液膜的切线方向.随着α的减小，小球受到的向上的表面张力逐渐增大，并在α=90°时达到最大值Fm，之后逐渐减小.若小球的重力小于Fm，则小球可以稳定的停留在液膜上，且α<90°；若小球的重力大于Fm，则小球将无法稳定停留在膜上并最终下落；当小球的重力恰好等于Fm时，小球恰好可以停留在液膜上，即临界状态，此时小球与液膜相切于两者的交点处(α=90°)，如图1所示.结合式(3)可得临界状态下液膜曲面满足的方程为[2]：

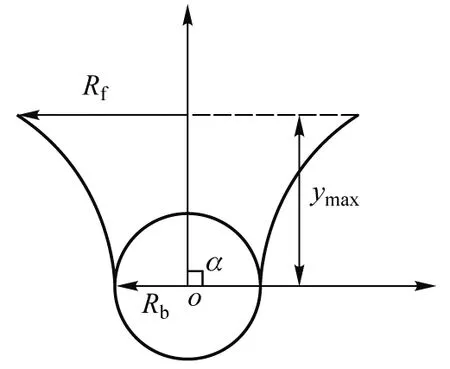
图1 能量小球边界条件示意图

(6)

其中Rf为膜的半径，Rb为小球半径，ymax为小球中心到膜的垂直距离.

解上述方程组(6)可得悬链曲面的最大扩张条件以及最大垂直扩张距离分别为：

(7)

将方程(7)绕y轴旋转后，得到液膜的表面积为

(8)

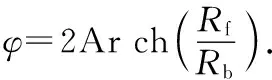
(9)

然后，当液膜和小球的交界线沿着小球下滑时，会有摩擦力造成的能量损失.根据杨式方程，摩擦力表现为液体移动时浸湿和干燥固体做功[4]：

dW=γωdl(cosθR-cosθA)

(10)

其中ω=2πRbsinα，θA为前接触角,θB为后接触角，α为小球与肥皂膜交线在截面上与小球竖直轴线形成的夹角，如图2所示.沿小球下滑曲线进行积分，其中α从0变化到π，可得小球打入液膜后沿液膜下滑摩擦造成的能量损失为

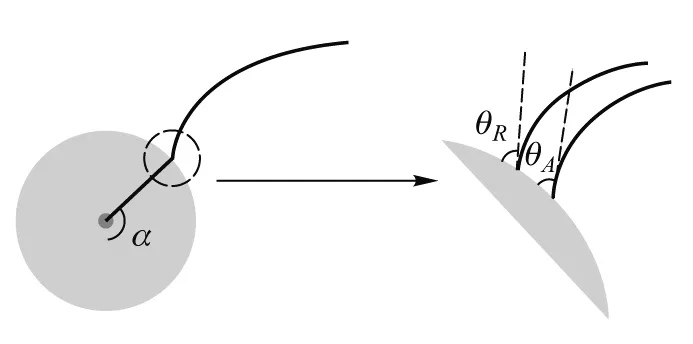
图2 杨式方程摩擦力接触角示意图

(11)

我们分别计算ln(ES/Ek)和ln(EP/Ek)随小球下落高度的变化曲线.基于实际实验参数，计算中小球半径取0.2 cm，膜半径取20 cm.表面张力系数γ从0.035 N/m变至0.065 N/m.数值计算结果如图3所示.摩擦耗能低于初打入能量和表面能增量3-4个数量级.因此，摩擦耗能可以忽略不计.

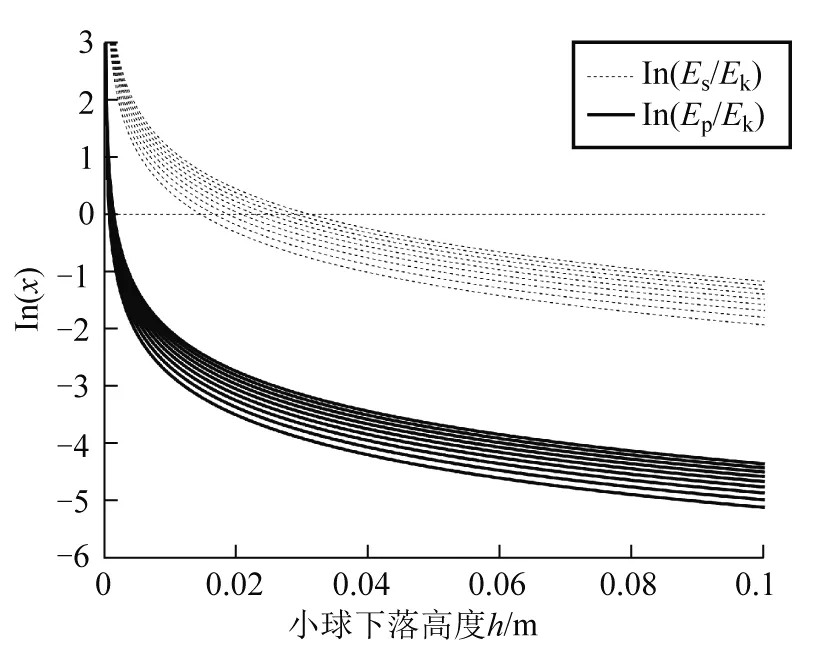
图3 ln(ES/Ek)和ln(EP/Ek)随小球下落高度的变化曲线

综上，在我们的实验条件下空气摩擦、液膜摩擦耗能均可忽略不计.表面能式(9)与动能式(4)之比，可给出小球与液膜相互作用过程的能量关系判定函数[4]：

(12)

若比值大于1，表明液膜极限表面能增量大于小球动能，小球能够停留在肥皂膜上；若比值小于1，表明液膜极限表面能增量小于小球动能，粒子将会穿透液膜；比值等于1即为液膜的临界透过条件.

2 实验验证

实验中我们配制不同表面张力系数的溶液(肥皂水)，测定配制溶液的YJ-JC-4A表面张力综合实验仪如图4所示.然后选取不同大小的塑料圈制备液膜.令不同规格、材质的小球穿过液膜进行实验.小球规格参数如表1所示.由于实验使用的小球半径、质量较小，不易制作精密的发射装置，因此实验中将套有不同表面张力系数的肥皂膜的塑料环固定在支架上，于肥皂膜上方不同高度处释放小球使其下落，通过重力势能转化为动能对实现小球穿过液膜的速度控制.

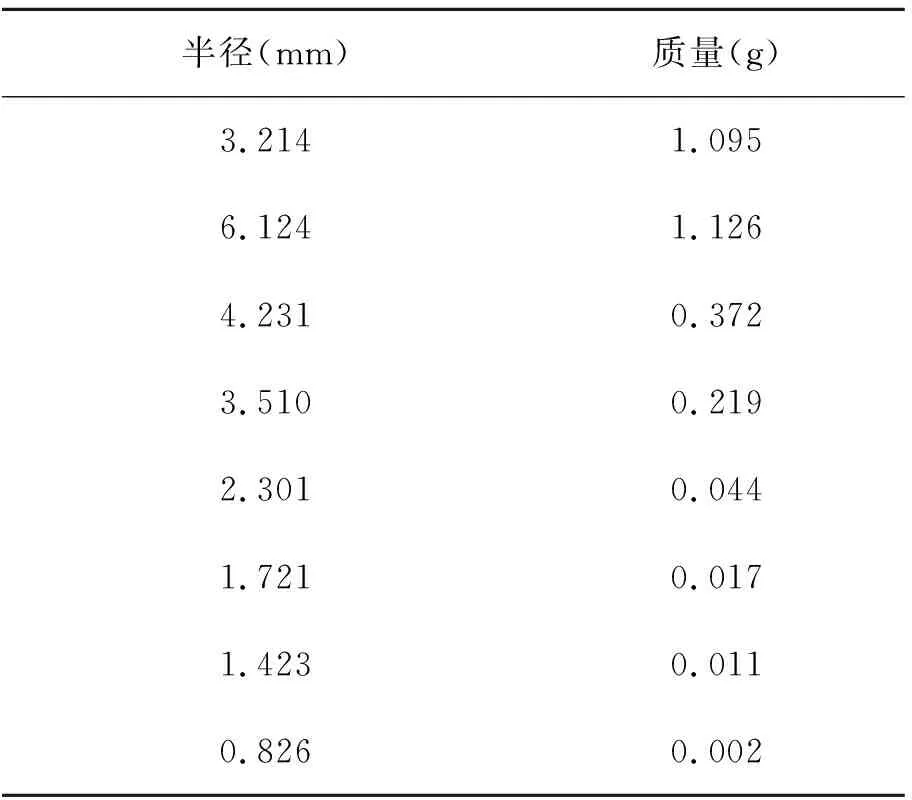
表1 小球材料与规格参数

图4 测量装置

2.1 悬链曲面验证

由1.1理论分析可知，肥皂膜在小球穿透的过程中始终保持悬链曲面.由于难以在下落过程中拍摄并提取清晰准确的帧，我们令铁球透过由直径为5.170 cm的塑料环形成的肥皂膜并将其置于桌上,如图5所示.此时铁球重力被桌子提供的支持力部分抵消，因此我们可将此时肥皂膜状态等效为粒子稳定停留在液膜上时的状态.使用Tracker对画面建立坐标系并进行定格描点.经测量，选取的时间帧中膜与铁球接触的圆环直径为2.273 cm.通过Tracker建立的坐标系记录膜上的5个点，获取坐标并带入Matlab中进行悬链曲面的拟合.

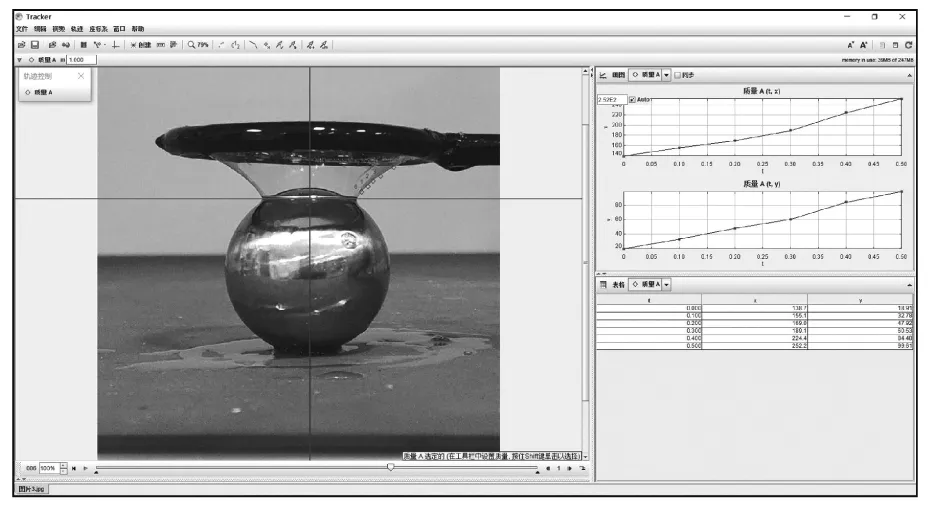
图5 实际Tracker帧分析采样示意图

为保证拟合的精度与合理性，我们分别在靠近塑料环、小球与肥皂膜交线的位置各进行了1个点的采样，并在中间高度进行了3个点的采样.图6为经Tracker帧分析导出的5个数据点在Matlab中的图像，其中上端虚线对应塑料环所处高度，其与实线的交点横坐标即为塑料环半径；下端虚线对应肥皂膜与小球交线(一个圆环)所处高度，其与实线的交点横坐标为交线环半径.菱形点为帧分析采样的5个数据点，实线为Matlab拟合的悬链曲线.由图可知，小球穿透过程中液膜形状符合悬链曲面模型，验证了1.1节的理论分析结果.

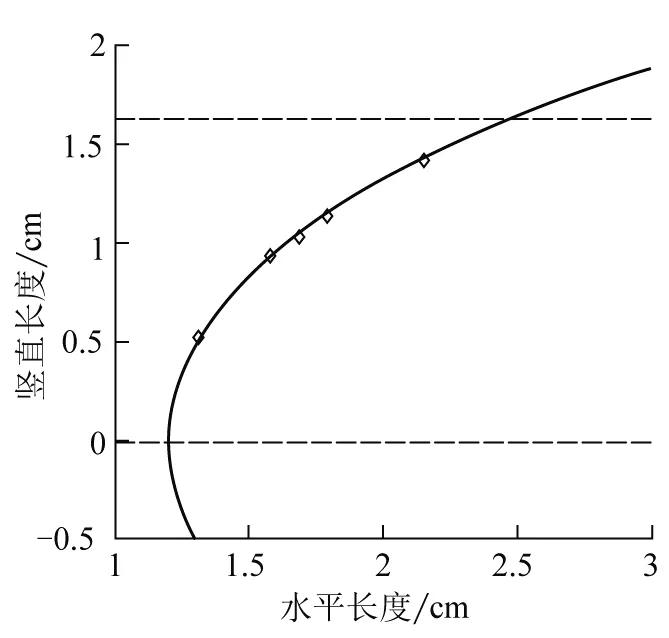
图6 悬链曲面模型验证图

2.2 临界透过条件验证

我们使用蜡和聚甲基丙烯酸甲脂(PMMA)两种材质的不同规格小球，通过调节小球初始释放高度验证临界透过条件，即式(12).图7—图9分别为液膜直径为5.170 cm、17.510 cm和25.215 cm条件下的实验结果图.图中横坐标为实验小球半径，纵坐标为实验小球的密度×初始释放高度.实验中，若小球最终穿透肥皂膜，则在图中相应坐标用实心圆点标记；若小球不能穿透肥皂膜，最终稳定停留在肥皂膜上，则在图中相应坐标处用空心菱形标记.同时，图中实线为满足临界透过条件，即ES/Ek=1，的对应曲线.在实线以下的部分，ES/Ek>1，即穿透过程中表面能大于动能，小球不能穿透肥皂膜并最终停留在肥皂膜上；实线以上的部分，ES/Ek<1，即穿透过程中动能大于表面能，小球最终能穿透肥皂膜.

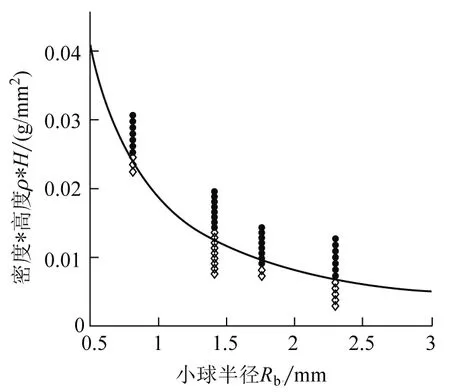
图7 膜直径5.170 cm条件下的临界透过条件验证图

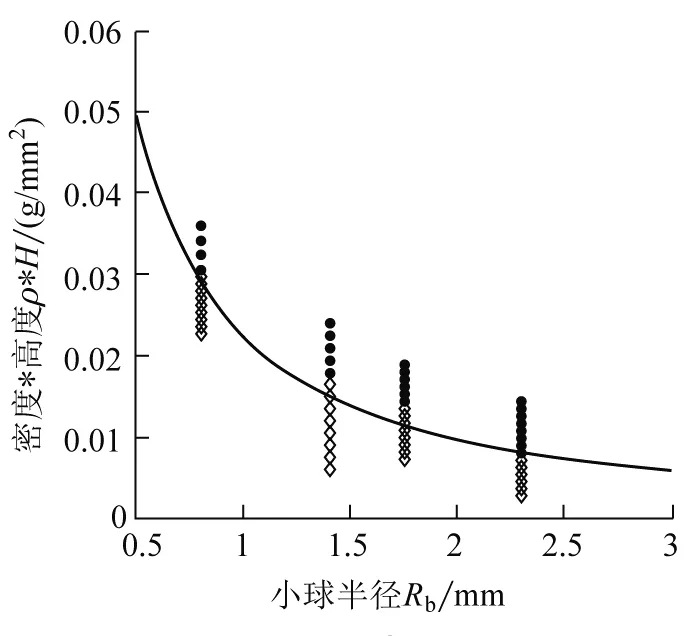
图8 膜直径17.510 cm条件下的临界透过条件验证图

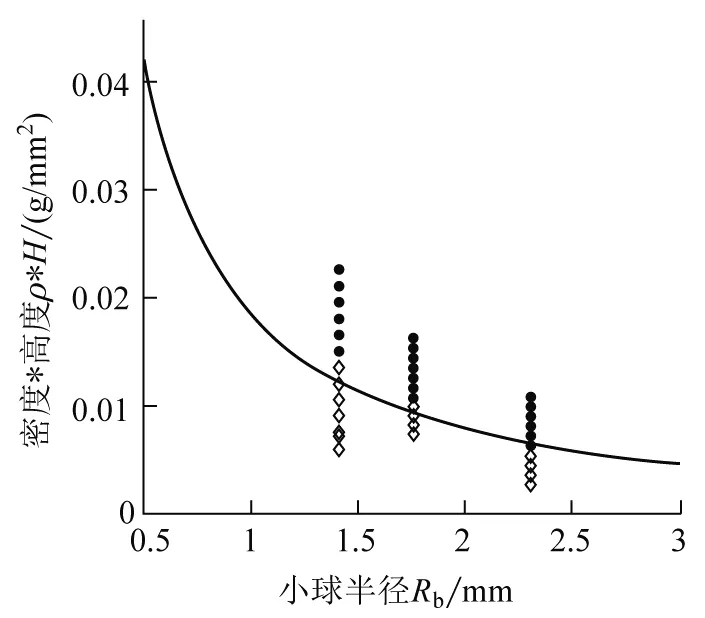
图9 膜直径25.215 cm条件下的临界透过条件验证图

图7—图9表明，实验结果较好的验证了理论上解析推导得到的小球临界透过条件，式(12)，的有效性.当小球半径较大(大于2 mm)时理论与实验结果吻合良好；而小球半径小于2 mm时，理论值与实验结果存在一定误差.这是由于当小球半径较小时，半径较小的小球在释放及下落过程中更容易受到阻力、气流扰动带来的影响；半径较大的小球在释放和下落过程中则表现出一定的稳定性.同时，我们可以看到，当从相同高度释放不同半径的小球时，大于临界透过半径的小球会穿过肥皂膜，而小于临界透过半径的小球会被留在肥皂膜上，实现了选择性透过功能.

2.3 小球速度筛选

对应临界透过条件，即ES/Ek=1，存在临界高度Hc，即小球从该高度下落时恰好停留在液膜上.式(12)表明，在小球参数确定的情况下，临界高度Hc与液膜表面张力系数γ成正比.将套有不同表面张力系数的肥皂膜的塑料环固定在支架上，于肥皂膜上方不同高度处释放小球使其下落，并记录小球的临界高度Hc.上一节中的实验结果表明，小球半径小于2 mm时实验结果与理论结果有一定偏差.因此，我们采用半径2.301 mm的石蜡小球进行实验.实验测得的小球临界高度与表明张力系数的关系如图10所示.其中，菱形标注为不同表面张力系数下的小球临界高度，直线为理论计算结果.

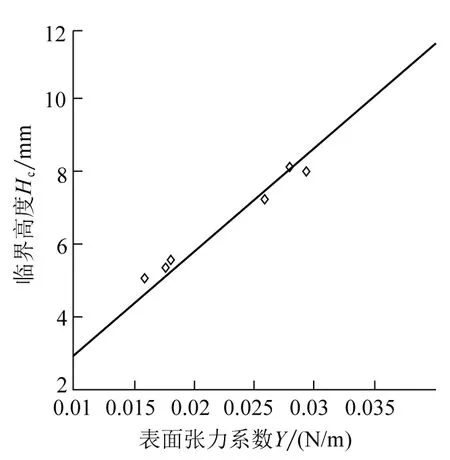
图10 表面张力系数与临界高度关系图

理论计算和实验结果表明，临界高度Hc与表面张力系数γ成线性关系.由实验设置可知，临界高度对应着小球的临界穿透速度.因此，当小球参数确定时，可以通过调节肥皂膜的表面张力系数，让速度大于临界穿透速度的小球透过肥皂膜，而保留速度小于临界穿透速度的小球，从而实现对小球速度的筛选.

3 总结

本文讨论了一种用肥皂膜制作的液膜过滤器，其特性是重粒子可以透过而轻粒子可以停留.本文从极小曲面定理入手，通过求解杨-拉普拉斯方程得到肥皂膜稳定时的悬链曲面模型；通过对粒子打入过程的动能、液膜表面能及摩擦耗能的分析与比较，得到了粒子打入过程的临界透过判定函数；实验上，首先通过粒子打入过程分析验证了悬链曲面模型的合理性，通过调节释放高度和小球半径对小球的临界透过条件进行验证.实验结果表明，在小球半径大于1.5 mm时与理论吻合较好.另外，基于小球临界穿透速度(高度)与液膜表面张力系数的线性关系，实现了对小球速度的筛选.为进一步深入细致研究液膜过滤器性质及应用提供了理论基础和实验参考.

4 致谢

致谢：感谢西安交通大学物理学院实验教学中心王雪冬老师对本实验的支持.