COVID-19 空气传播的动力学研究
2022-05-05欧忠文刘俊兵王月明
欧忠文,刘俊兵,王月明
(山西大学 物理电子工程学院,山西 太原 030006)
自 2019 年底以来,COVID-19 病毒已经对全球人民的生命健康造成了巨大的灾难和威胁,截至2021年8月3日全球被感染人数达 198 778 175 人,死亡 4 235 559 人[1].各国人民和政府采取各种措施从不同层面共同抵抗COVID-19 病毒的传播[2-4].我们知道,通常由于咳嗽、打喷嚏、说话或者呼吸所释放出的液滴会包含大量致病的微生物,比如细菌、病毒、真菌等.携带病原体的液滴能通过呼吸系统以气溶胶的形式或者以握手等直接接触的方式从一个被感染者转移到一个健康者身上.建立数学和物理模型来解释和预估 COVID-19 病毒的空间和时间传播属性也是一个研究热点[5-7].在本文的研究中,我们针对不同大小的液滴采用不同的物理模型,分别用牛顿运动方程和扩散方程来描述液滴的运动,计算液滴在正常呼吸、咳嗽或打喷嚏时的水平漂移距离、扩散距离以及在空气中的滞留时间,特别在液滴半径非常小的时候我们对空气黏度进行了修正.
1 模型说明
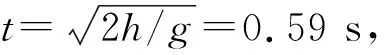
2 竖直方向上的动力学方程
首先考虑在竖直方向上在重力和黏滞力作用下的动力学方程,其中液滴半径为r(0.05~100 μm),液滴的质量为m,液滴的密度ρs=103kg/m3,空气密度为ρg=1.29 kg/m3,当液滴半径非常小的时候,其量级接近空气分子的平均自由程,故要考虑空气黏度的修正η′=η/(1+b/pr).而当液滴的半径较大时有η′=η,故我们直接用η′替代η,从而使得黏度的形式不发生变化,其中空气的黏度η=1.82×10-5Pa·s,修正系数b=6.17×10-5m·mmHg,大气压强p=760 mmHg,此时空气对于球形液滴的黏滞力可以写为f=6πη′rv,当然雷诺数要满足Re=ρgvr/η′<1[11],在后面我们会证明空气黏滞力的形式在大范围内是准确的.从而我们可以写出牛顿动力学方程:
(1)
考虑到人体通过正常呼吸或是咳嗽、打喷嚏排出的液滴在竖直方向上没有初速度,即方程的初始条件为v(0)=0 m/s,这样我们便可以得到竖直方向速度的含时解为
(2)
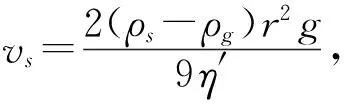
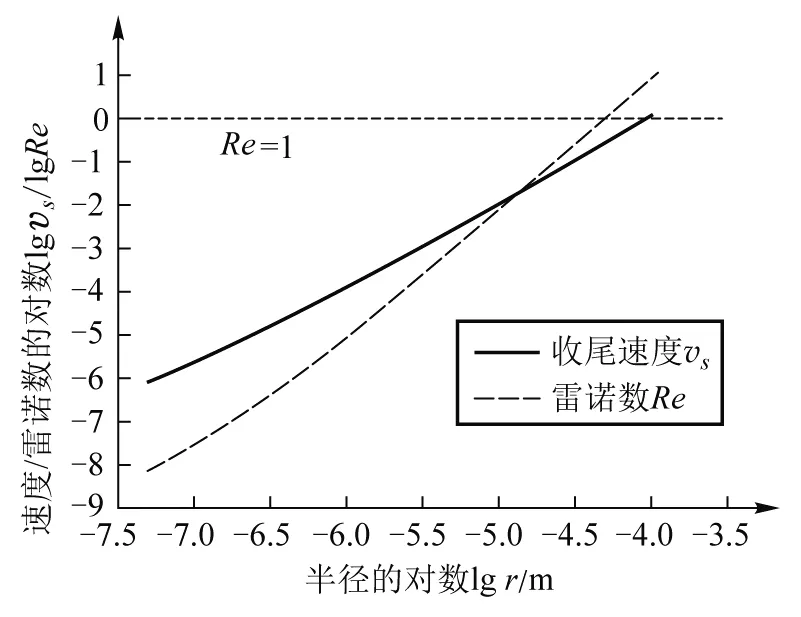
图1 收尾速度以及达到收尾速度时的雷诺数
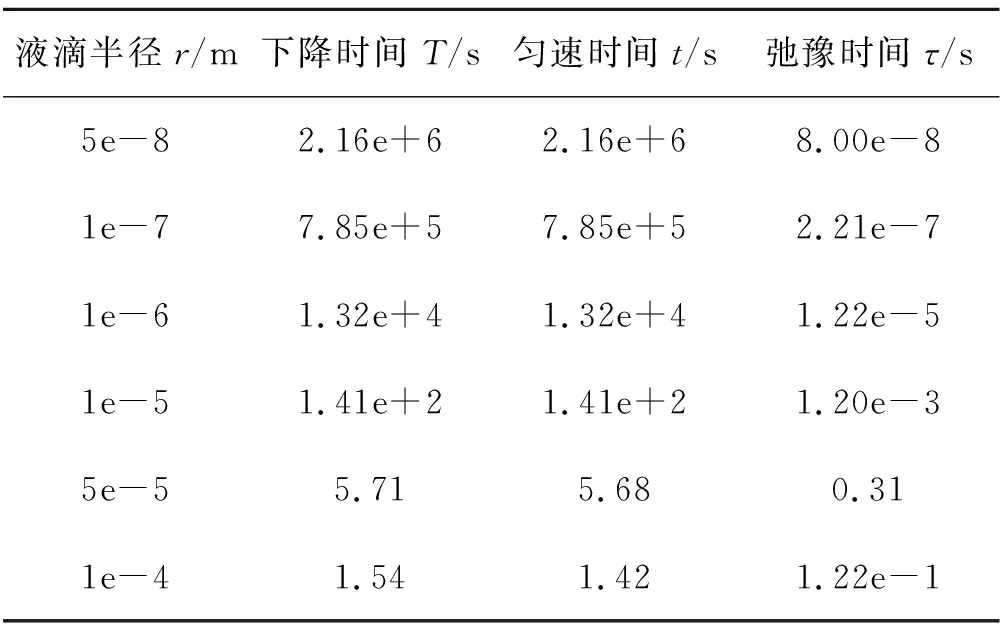
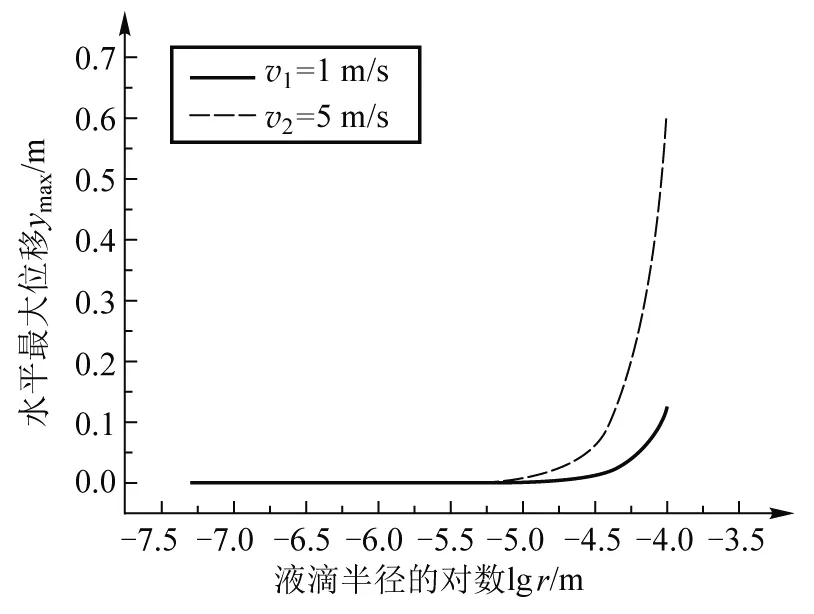
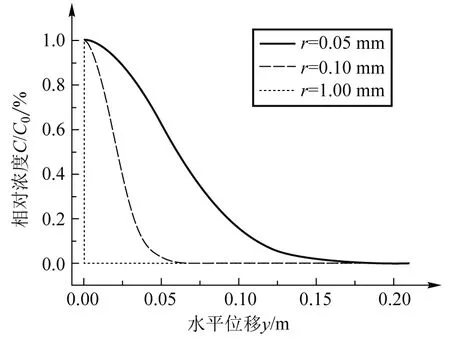
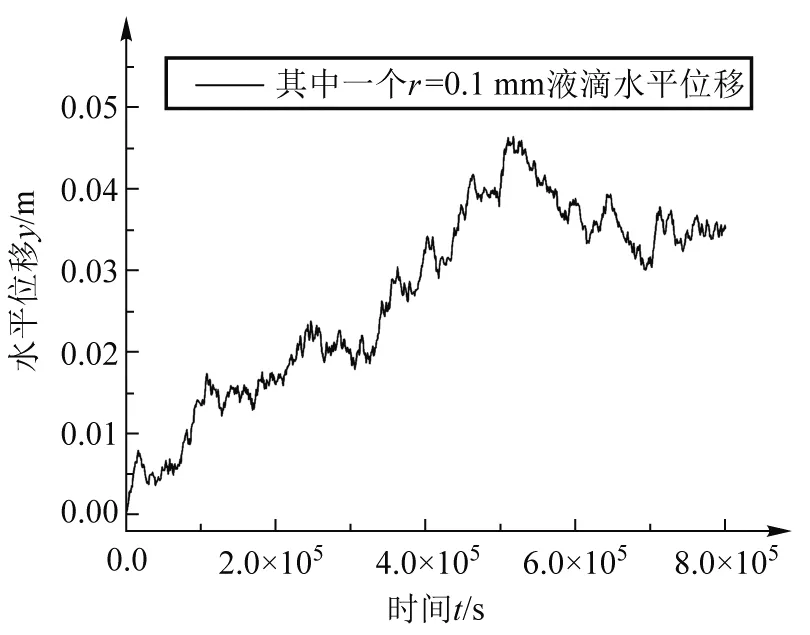
从上面的图1中可以看出液滴的半径r<50 μm时,在此范围内满足雷诺数Re<1,即在此范围内黏滞力的形式是准确的.而当50 根据上面的结果,可以假设一个匀速运动时间t.从人口腔排出液滴的一般高度为h=1.7 m,我们暂时忽略液滴在空气中的向下加速过程,下面我们会证明这个假设是合理的,此时我们假设全程以收尾速度运动,其运动的时间t=h/vs,同时根据上面的计算结果知道弛豫时间τ,即到达(1-1/e)vs所需时间.图 2给出了不同半径下t和τ的变化趋势图. 图2 不同半径液滴的匀速运动时间和弛豫时间 从图 2 中可以看到弛豫时间和匀速运动时间不在同一个量级,可以看出匀速运动时间t>>τ,即可以忽略弛豫时间或者说是加速到收尾速度这一段时间,此时在竖直方向上液滴的运动可以近似为一段以收尾速度做匀速运动的过程[10].同时根据下面的表格(T是考虑到加速过程的运动时间),可以看出当液滴半径很小的时候,有T=t,而在液滴半径接近100 μm时,有T≈t.也可以看出下落时间随液滴半径逐渐增大而减小,且当液滴半径在病毒尺寸时,可以在空气中停留长达25 天,当然前提是病毒在空气中的寿命可以达到这个时间.当半径r=1 μm时,液滴在空气停留的时间为3.7 h,而当半径到了100 μm时停留时间只有1.5 s,此时液滴会在短时间内下落到地面. 表1 不同半径液滴各种时间的比较 接下来我们继续考虑液滴在水平方向上的动力学方程,可以知道水平方向只受到黏滞力作用,且通过人体正常呼吸排出液滴的速度一般为v1=1 m/s,通过咳嗽或者打喷嚏排出的液滴速度一般大小为v2=5 m/s[10],即可以得到水平方向的初始条件为vy(0)=v2,同时根据初始速度v2=5 m/s和液滴半径r=100 μm,可以计算得到最大的雷诺数Re=36.当1 (3) (4) (5) 根据水平速度的表达式,可以看出水平方向的速度呈指数衰减,当t=τ时,vy=vy(0)/e ,根据前面计算可知,τ远小于运动时间T,所以我们可以将水平运动最远距离写为ymax=vy(0)τ,图 3 给出了不同速度和半径的液滴在水平方向上运动的最大距离. 图3 不同半径液滴的水平运动最大距离 (6) (7) (8) 图4中的结果是在经过沉降时间T后得到的溶度分布,其中相对溶度是指相对y=0处的溶度,可以看到对于一定半径的液滴,其扩散溶度会迅速减少,而随半径的增大,能够扩散到的范围也会逐渐减少,当r>1 μm时,可以扩散的范围y<2 mm,也就是说r>1 μm时扩散效应可以忽略,关于这一点前面已经说明.当r=0.1 μm时,扩散范围也可以达到6 cm,而当半径r=0.05 μm,即达到病毒线度时,水平方向上的扩散范围最大可达到17 cm,此时扩散效应已经相当明显 , 当然此时我们并没有考虑到竖直方向扩散效应对液滴沉降时间的影响,通过后面的数值计算我们将说明这是合理的. 图4 经过沉降时间T水平方向液滴的扩散分布 从上面可以看出当r<1 μm时,扩散效应已经不能忽略,此时必须考虑在竖直方向上扩散效应对沉降时间的影响,而沉降时间又会影响水平扩散分布.根据前面分析可知此区间的液滴在竖直方向会迅速达到收尾速度,即此时在竖直方向上∑Fi-γvs=0,其中Fi为外力,γ=6πη′v,而在水平方向上速度也会迅速减为零,这都是上面已有的分析结果.考虑到布朗运动,此时我们利用朗之万方程[15,16]: (9) (10) 其中初始条件为xi(0)=0和yi(0)=0,考虑到粒子运动时间过长以及步长对BD方法模拟无影响[18,19],故我们选择的步长Δt=1 000 s,当有一个微粒在竖直方向运动的距离x=h=1.7 m时,我们便停止计算,经过数值计算[17,18],得到下列结果(见图5,图6). 图5 经过沉降时间T后半径r=0.1 μm 液滴的模拟结果 图6 经过沉降时间T后半径r=0.05 μm液滴的模拟结果 从图中我们可以得r=0.1 μm时,液滴在空气中的扩散时间在7.7×105s左右,水平方向上有少数液滴可以扩散到5 cm处,大部分扩散范围在3 cm;对于r=0.05 μm的液滴,液滴在空气中的扩散时间在2.0×106s左右,在水平方向上有少数液滴可以扩散到15 cm,大部分扩散范围在10 cm以内.我们可以看到理论计算与数值计算的结果几乎是一致的,同时也可以得到这样的结果,即扩散效应对沉降时间并无多大影响. 从图中我们可以得r=0.1 μm时,液滴在空气中的扩散时间在8×105s左右,水平方向上有少数液滴可以扩散到5 cm处,大部分扩散范围在3 cm;对于r=0.05 μm的液滴,液滴在空气中的扩散时间在2.2×106s左右,在水平方向上有少数液滴可以扩散到15 cm,大部分扩散范围在10 cm以内.我们可以看到理论计算与数值计算的结果几乎是一致的,同时也可以得到这样的结果,即扩散效应对沉降时间并无多大影响. 通过上面的理论计算和数值计算发现,我们关注的半径r范围是0.05~100 μm,当r>10 μm时,通过正常呼吸或者咳嗽排出的携带病毒液滴在空气中停留的时间为1.5~140 s, 但是通过咳嗽和打喷嚏可以将病毒运送到0.61 m处,而通过正常呼吸,病毒在水平方向的运动距离为0.12 m.而对于半径在1 μm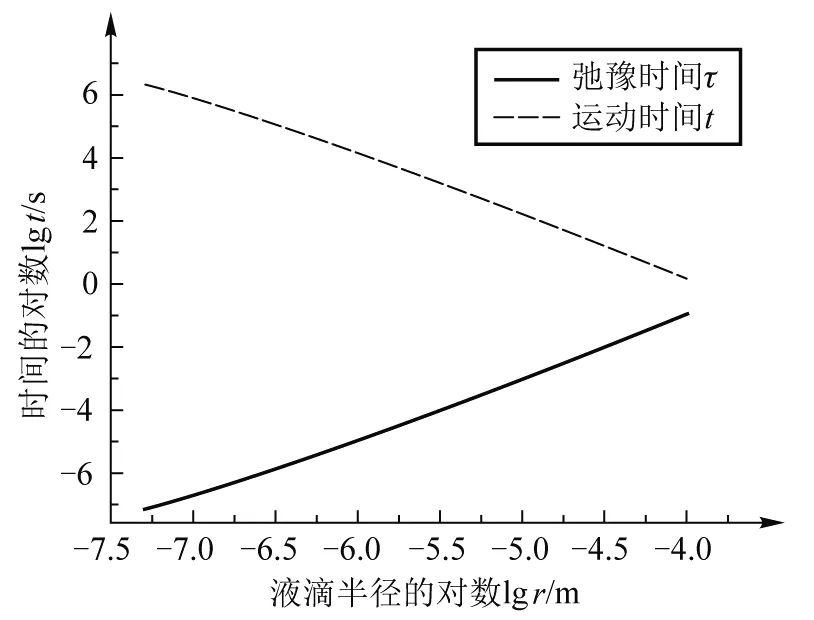
3 水平方向上的动力学方程
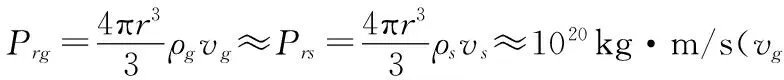
3.1 扩散方程
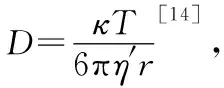
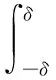
3.2 数值计算
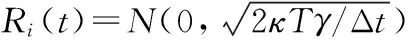

4 总结
