通过完整的麦克斯韦方程导出电磁场的相对论变换
2022-05-05黄永义
黄永义
(西安交通大学 物理学院,陕西 西安 710049)
电磁场相对论变换的导出对于理解狭义相对论是必要的,有好几种导出的方法.1905年爱因斯坦创立了狭义相对论,把洛伦兹变换应用到真空的麦克斯韦方程,由简单的偏导数变换第一次导出了电磁场的相对论变换公式[1].相对性原理要求麦克斯韦方程在所有惯性系都成立,麦克斯韦方程可以写成电磁场张量Fμv的形式,从电磁场张量的变换公式也能导出电场强度E和磁感应强度B的变换公式[2-4].不过张量和张量变换对学生来说有点抽象,不易理解.带电粒子在电磁场中运动受到洛伦兹力q(E+v×B),其运动满足牛顿方程dp/dt=q(E+v×B),从dp/dt和速度v的变换也能导出电磁场的变换公式.这种变换实际上用带电粒子的动力学定义了电磁场,导出过程需借助于相对论力学,因此不够直接[5,6].Smith和Purcell考虑了不同惯性系中电荷分布和电流分布的变换关系,可以推导出两个惯性系中电磁场的关系,实际上也完成了电磁场的变换[7,8].一个惯性系中大的平行板电容器两极板间存在匀强电场,在运动的惯性系观测两极板间存在的电场和磁场,应用相对论速度合成公式和电荷不变假设,Griffiths得到电磁场的变换[9].Jefimenko从电磁场推迟势的积分也导出了电磁场的变换[10].Ferraro从平面电磁波在所有惯性系中都是平面波这个事实出发直接得到了电磁场的变换关系[11].也有一些作者采用了类似爱因斯坦的做法,先从电荷守恒定律的协变性导出电流密度矢量j、电荷密度ρ的相对论变换,在此基础上从完整的麦克斯韦方程进一步导出其他电磁场(电场强度E,磁感应强度B,电位移矢量D,磁场强度H)变换关系[12,13].一般的共识是电荷守恒定律是麦克斯韦方程的推论,因此借助于电荷守恒定律的协变性再从完整的麦克斯韦方程导出电磁场的变换总觉得不够严谨.本文避开电荷守恒定律的协变性,只从完整的麦克斯韦方程和相对性原理导出电磁场之间的相对论变换关系:电场强度E,磁感应强度B,电位移矢量D,磁场强度H,电荷体密度ρ和电流密度矢量j.首先导出磁感应强度B、电场强度E的变换关系,其次导出电位移矢量D、电荷密度ρ的变换关系,再次导出磁场强度H和电流密度矢量j的变换关系,最后给出文章小结.
1 导出磁感应强度、电场强度的相对论变换
考虑两个参考系S和S′,它们的3个坐标轴相互平行且方向相同,S′系沿S系x轴方向以速度u匀速直线运动.参考系里的时空坐标分别为(x,y,z,t)和(x′,y′,z′,t′),为了简单,假设初始时刻S系和S′系的坐标原点重合.两个参考系时空坐标的洛伦兹变换为
(1)
式中c为真空中的光速,γ=(1-u2/c2)-1/2.洛伦兹逆变换为
(2)
从洛伦兹变换式(1)及逆变换式(2)可得如下微分关系:
(3)
S系完整的麦克斯韦方程为
(4)
式中B为磁感应强度,E为电场强度,D为电位移矢量,ρ为电荷体密度,H为磁场强度,j为电流密度矢量.相对性原理要求S′系中对应于S系的麦克斯韦方程式(4)为
(5)
S系中,对于B,式(4)具体为
(6)
S′系中对应式(4)的式(5)具体为
(7)
将微分关系式(3)应用到式(6)可得
(8)
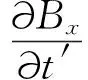
(9)
将微分关系式(3)应用到式(9)可得
(10)
将式(10)代入式(8),整理得
(11)
式(11)和式(7)对照,得磁感应强度的变换关系:
(12)
从两个微分方程式(11)和式(7)相同,可以得出被求导的电场强度分量、磁感应强度分量相同的结论,即式(12),其原因是两个微分方程中除了被求导的电磁场分量以外,其他都是一致的,那么两个方程中被求导的对应位置的电磁场分量应当是一致的.当然严格来说,两个方程对应位置的电磁场分量还包含一个以牵连速度u为自变量的函数因子,爱因斯坦已证明这个函数因子只能等于1[1].
为了导出电场强度的变换关系,我们需要式(4)和式(5),它们的分量形式分别为:
(13)
(14)
将微分关系式(3)应用到式(13),可得
(15)
将式(7)和式(12)代入式(15)可得
(16)
将式(16)和式(14)对照可得电场强度y分量、z分量的变换:
(17)
为了得到Ex的变换,将微分关系式(3)应用到式(13),得
上式整理可得
(18)
(19)
2 导出电位移矢量、电荷密度的相对论变换
S系中式(4)和S′系中式(5)的第3式可写为
(20)
(21)
将微分关系式(3)应用到式(20),可得
(22)
(23)
将微分关系式(3)应用到式(23),得
(24)
将式(24)代入到式(22)可得
(25)
式(25)和式(21)对照可得电位移矢量和电荷密度的变换关系:
(26)
3 导出磁场强度、电流密度矢量的相对论变换
为了导出磁场强度的变换关系,我们需要式(4)和式(5),它们的分量形式为
(27)
(28)
(29)
将式(21)代入式(29),得
(30)
将式(26)变换代入式(30),注意1+γ2u2/c2=γ2,得
(31)
式(31)和式(28)对照可得磁场强度y分量、z分量,电流密度x分量的变换关系为
(32)
将微分关系式(3)应用到式(27)得
(33)
式(33)整理一下,得
(34)
式(34)和式(28)对照,可得Hx、jy的变换关系为
(35)
将微分关系式(3)应用到式(27)得
(36)
式(36)整理后得
(37)
(38)
4 小结
通过完整的麦克斯韦方程和相对性原理我们直接导出电场强度E、磁感应强度B、电位移矢量D、磁场强度H、电荷体密度ρ和电流密度矢量j的相对论变换.计算过程有点繁琐冗长,但很容易被学生掌握,因为他们仅仅需要对函数的偏导数的知识.计算的逻辑也很清楚,就是麦克斯韦方程,包括它们的分量方程都要满足相对性原理,即物理定律的形式在所有的惯性系中都相同,因此本文有助于学生深刻理解麦克斯韦方程和狭义相对论.在导出电磁场的相对论变换过程中只使用了完整的麦克斯韦方程的协变性,而没有使用电荷守恒定律的协变性,从一个侧面也说明电荷守恒定律只是麦克斯韦方程的一个推论.
