基于高斯声束模型解释水中声速测量异常现象

王可欣，周诗韵

(复旦大学 物理学系，上海 200433)

共振干涉法测量声速是高校经典物理实验之一，其原理和实验现象备受关注和讨论[1-3].通常，其物理模型被描述为：接收换能器与发射换能器的表面互相平行，从发射换能器发出的平面波与接收换能器反射的波干涉叠加，形成驻波.因此，当接收换能器逐渐远离发射换能器时，会经过一系列波腹，表现为接收声压经过一系列极大值，且间距恰好为声波的半波长.结合声源的频率，即可计算得到声速[4].这种方法可以用于测量空气和水中的声速，对于学生理解波的反射与叠加很有帮助.

然而，该物理模型作了一定程度的简化，实际上只是一个一维模型，并没有考虑一些实际因素.例如，实验室中的发射换能器是有限大小的活塞，不能发射理想的平面波；测量水中的声速时，容器大小有限，导致声波在水缸壁、水面上也有反射.因此，简化模型无法完全解释实验现象，如声压幅值的异常变化、次级大现象等.已有文章指出，使用换能器间多次反射叠加和球面波模型修正[5,6]，或者二次相位合成的方法[7]，可以解释空气中的近场效应[8]；考虑水-空气界面反射，可以解释水中异于空气中的特殊现象，即声压极大值随换能器间距的非单调变化[9].然而，到目前为止，还没有定量解析此异常现象与水面高低关系的报道.由于水中声场会在水-空气以及水-水缸壁界面发生反射，使用球面波模型非常复杂.常见的点对点积分(point-by-point integration)也很难处理该情况，当考虑四周界面反射时，难以确定接收换能器上的每一个点的声压到底由哪些反射贡献.

为模拟水中的声波反射叠加，引入多元高斯声束模型[10,11]，将换能器发出的声束拆分为一组高斯声束的叠加，并借用光学镜像法中虚光源的概念[12]，提出虚声源模型，最终根据一定标准进行截断，得到反射叠加后接收换能器上声压的解析表达式.数值计算结果表明，模拟得到的声压极大值与距离的关系与实验现象相符，且整体变化模式与水位的关系与实验结果一致.

1 实验现象与结果

实验装置示意图如图1所示.不考虑换能器发出或接收声波的电声耦合过程，将换能器等效为半径为a的刚性圆板，且不计其厚度.发射换能器位于左侧水缸壁，其中心到水缸前后侧壁的距离是b，到上水面的距离是hu，到水缸底的距离是hd，接收换能器正对发射换能器，相距为d.

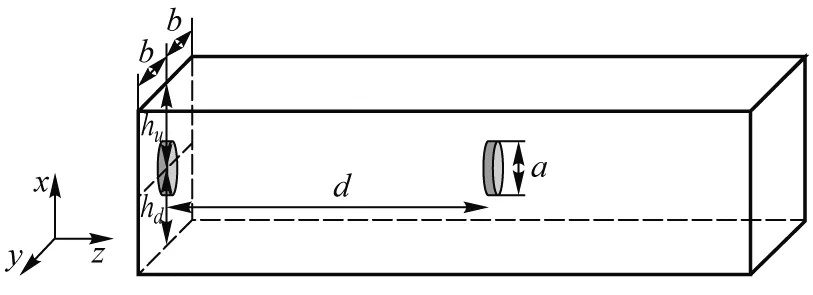
图1 实验装置示意图

实验开始时，换能器相距5 cm，再逐渐移动接收端，使两者间距增加，测量并记录出现的声压极大值及其位置.在相同条件下，仅改变水缸内液面的高度，并始终保证液面高于换能器探头，进行多组实验.以单次实验中首次出现的声压极大值p0进行归一化，作声压的相对大小p/p0随位置的关系图，如图2所示.可以发现，声压极大值并非随换能器间距增加而单调递减，而会在一定情况下发生反弹，且反弹的幅度及位置与水位h=hu+hd有关.

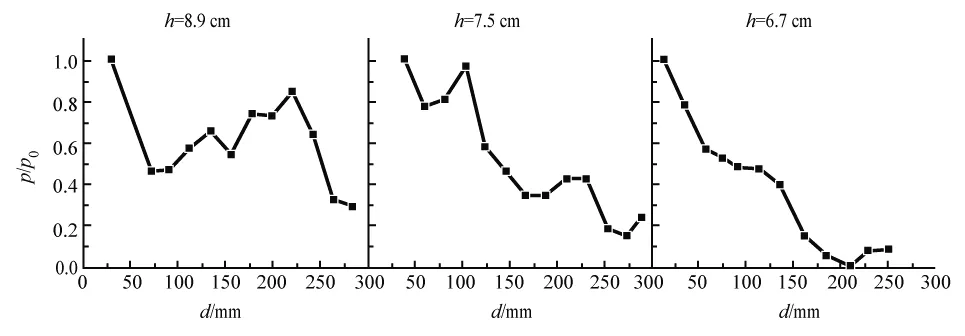
图2 声压极大值随距离变化的异常现象.从左到右，水位h分别为8.9 cm、7.5 cm和6.7 cm

如果仅使用驻波模型，声压极大值应该不随换能器间的距离而发生变化；如果考虑声波传播中的衰减损耗，则声压极大值应该随换能器间距单调减小.因此，观察到的声压极大值反常变大的现象不能用已有模型或者常识简单推演解释.注意到随着液面降低，反弹幅度减小，反弹出现的位置延后.该现象说明液面高度的变化对声压极大值的影响较大，据此推测，液面的反射是重要影响因素之一.

2 理论推导和模型建立

理想模型中，换能器发出的平面波仅在换能器之间反射[4]，则液面高度对声压测量值无影响.因此，必须假设声场分布发散，才能引入液面处的反射.同时，理想的平面波应由无限大平板产生，而实际情况下，换能器探头尺寸有限，客观上也不满足激发平面波的条件.因而，使用非平面波声场来修正物理模型是十分合理和必要的.本实验中圆形换能器的声场，可以用多元高斯声束的模型来近似处理，而该声场在界面处的反射，可以用虚声源的模型计算处理.

2.1 多元高斯声束模型

假设换能器的探头是绝对刚性的正圆铝片，振动发声，其振动速度V(r)垂直于探头表面，且满足下列函数关系：

(1)

其中r是探头所在平面内任一点到探头中心的距离，a是探头的半径.设其对应的声波的速度势为ψ，则根据Helmholtz方程有

2ψ(r,t)+k2ψ(r,t)=0

(2)

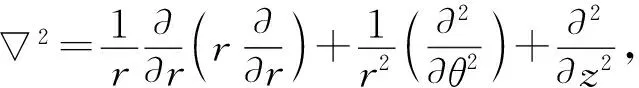
(3)

再假设试解u(r,z)=g(z)ef(z)r2，代入式(3)可以得到

(4)

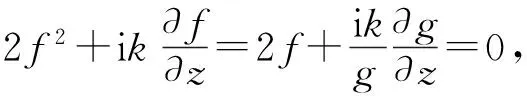
(5)

其中B是任意常数.因此速度势可以写成N个系数为an、形式为高斯函数的解的叠加，即

(6)

这就是多元高斯声束模型[10].

在该模型中，参与叠加的高斯声束数目N越多，模拟声场的结果就越准确.但对于圆形换能器在远场部分的辐射声场，仅使用15个高斯声束叠加，即可较好地描述[13].这里远场的定义为距离换能器表面大于菲涅耳距离z0=a2/λ的部分，其中a是探头的半径，λ是超声波的波长.若进一步增大N，例如N=25，将使更靠近换能器的声场描述更加准确，而对远场影响不大.此外，即使增大到无穷项，该模型也无法描述距换能器表面小于换能器直径2a范围内的声场[13].在本实验中，菲涅耳距离为2 cm，而本文关心的是5 cm之外的声场，因此，使用15个高斯函数进行叠加即可.

(7)

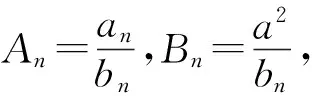
(8)

其中系数An和Bn的确定可用拉格朗日乘子法，具体结果见表1[14].

表1 高斯声束系数[14]

使用与实验中一致的参数进行模拟：水的密度ρ=997.7 kg/m3，水中声速c=1 489 m/s，换能器发射信号频率υ=36.22 kHz，半径a=1.9 cm，换能器中心距离水缸两侧壁距离b=3.0 cm，距离上水面距离hu=3.0～6.0 cm，距离下界面hd=3.0 cm.

首先利用这15个高斯型函数模拟刚性平面圆板表面的声压，结果如图3所示，模拟效果较好.如果假设的圆板非绝对刚性，即速度分布在圆板边缘不是阶跃函数，则模拟所需的高斯函数数量甚至可以进一步减少.此后，在不考虑反射的情况下，模拟计算该高斯声束的归一化声场，x=0的横截面的声压幅值分布图如图4所示，注意图4中纵坐标范围是±4b，其中虚线表示y=±b的位置，即水缸侧壁.从图4中可见，换能器声场的发散不可忽略.同时，由于圆形换能器具有中心对称性，在当前实验条件下，需要同时考虑水缸侧壁和上下界面的反射声场.

图3 绝对刚性圆形平板表面声压分布模拟.其中pc是平板表面中心声压，用于归一化

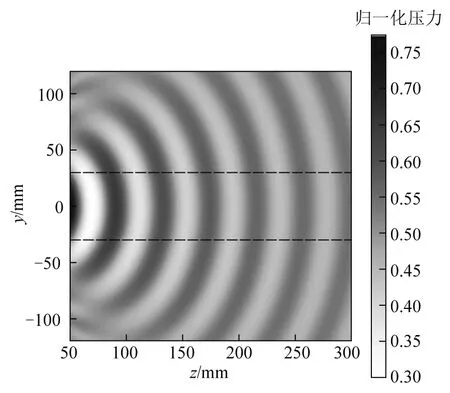
图4 x=0横截面处，不考虑反射时的多元高斯声束声场分布.虚线表示水缸侧壁位置

2.2 虚声源模型

类比于光学镜像法中虚光源的处理方法[15]，可以认为声压经水-空气、水-水缸壁界面反射后，对接收换能器的作用相当于一个与原声源关于界面对称处的等大虚声源直接发射的声场到达接收换能器的效果.从水入射到介质x的反射系数rx由声阻抗Z计算得到

(9)

在模拟计算中，取水的声阻抗为1.489 3×106kg/(m2·s)，铝制换能器的声阻抗为1.702 4×106kg/(m2·s)，水缸壁材质为有机塑料，声阻抗为3.176 6×106kg/(m2·s)，空气的声阻抗为411.60 kg/(m2·s)[16].计算可得，水-空气界面反射系数rair=-0.999 4，水-水缸壁界面反射系数rtank=0.361 6，水-换能器界面反射系数rpiston=0.839 1.

如果考虑处于位置(x,y,d)处的微元接收到的声压，则仅经过一次水-空气界面反射的声线的贡献如图5所示，可以表示为

图5 x方向虚声源模型示意

rair·p(x-2hu,y,d)

(10)

而仅经过一次y=-b处的水-水缸壁界面反射，如图6所示，相当于叠加上声压：

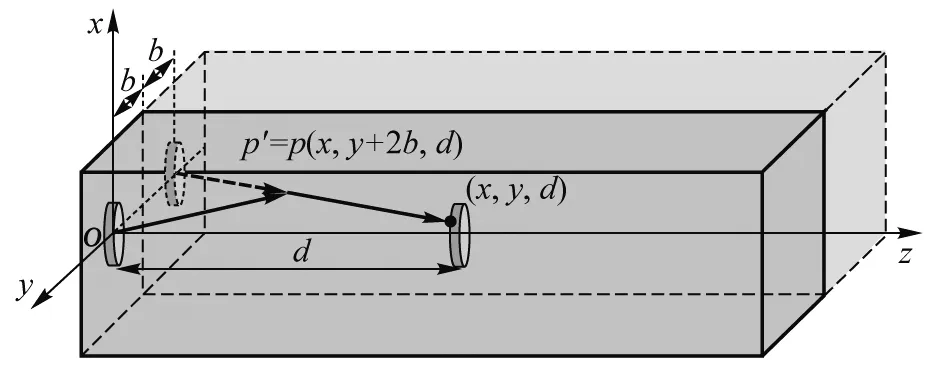
图6 y方向虚声源模型示意图

rtank·p(x,y+2b,d)

(11)

以此类推.

由于声波在水中衰减很小(α=2.621×10-4dB/m)[14]，理论上声场可以在各种界面上进行无限次反射，这必将导致虚声源模型的结果不能收敛[6]，因此必须在模拟计算中进行人为截断.本文的截断标准是：其他界面的反射声压不能大于换能器之间的直接反射声压pdirect，同时，为计算方便，忽略比pdirect小一个数量级以上的反射声压.因此，在模型中，最多只考虑3次界面反射，列出如下8种不同的反射途径.

1)直接到达对侧换能器的声压.

经数值计算可知，在实验条件范围内(5～30 cm)，至少需要20次反射，才能令接收声压不再随反射次数的增加而变化，因此有

(12)

2)只经过一次水-空气界面反射：

pair-water(x,y,d)=rair·p(x-2hu,y,d)

(13)

3)只经过一次水-水缸壁界面反射：

ptank-water(x,y,d)=rtank·p(x+2hd,y,d)

+rtank·p(x,y±2b,d)

(14)

4)只经过一次水-空气和一次水-水缸壁界面反射：

peither-one(x,y,d)=

rairrtankp(x+2hu+2hd,y,d)+

rairrtankp(x-2hu-2hd,y,d)+

rairrtankp(x-2hu,y±2b,d)

(15)

5)只经过两次水-水缸壁界面反射：

(16)

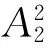
6)只经过三次水-水缸壁界面反射：

(17)

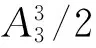
7)只经过两次水-水缸壁和一次空气-水界面的反射：

p(x±2(hd+hu),y±2b,d)]

(18)

8)只经过一次水-水缸壁和两次空气-水界面的反射：

(19)

通过以上分析可以看出，各反射途径贡献声压的相对大小，与水位h、换能器间距d、换能器表面具体位置(x,y)均有关.其中2)—8)中的反射声压大小相对于直接反射声压pdirect，在水位h=8 cm，间距d=25 cm时取得最大值，因此在此条件下考虑截断条件.

作出反射途径1)—8)中声压的相对值(即p/pdirect)在接收换能器x=0横截线上的大小随y坐标的变化，如图7所示.可以发现，除了反射7(即ptank2-air1)外，其他的反射声压都低于直接反射声压pdirect.因此，反射7)可能是虚声源带来的发散效应，在理论计算中不予考虑.综上，接收换能器上总声压为

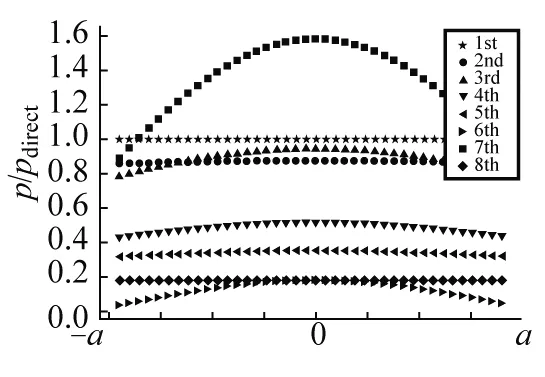
图7 h=8 cm,d=25 cm时，接收换能器x=0横截线上反射函数1)—8)的声压相对途径反射函数1)(pdirect)的大小随y坐标的变化，其中换能器半径为a

p(x,y,d)=pdirect(x,y,d)+pair-water(x,y,d)+

ptank-water(x,y,d)+peither-one(x,y,d)+

ptank2(x,y,d)+ptank3(x,y,d)+

ptank1-air2(x,y,d)

(20)

3 结果与讨论

由图7还可以发现，在换能器表面声压变化幅度较小，因此可以用中心点声压p(0,0,d)的实部而非积分值代表与发射换能器相距d处的接收换能器感受到的总声压，即实验测量声压值.代入数值后，计算声压p极大值随距离的变化，每种水位下均用第一个极大值进行声压的归一化，结果如图8所示.可以发现，模拟结果中也出现了与实验相似的异常现象，即声压极大值随换能器间距的增加而呈现非单调变化.当降低水面高度h时，该异常反弹的幅度减小，位置延后.这一变化模式和相同水位下的实验现象(图2)较为符合.由此，本文认为使用多元高斯声束模型和虚声源模型可以较好地描述水中声速的测量实验.

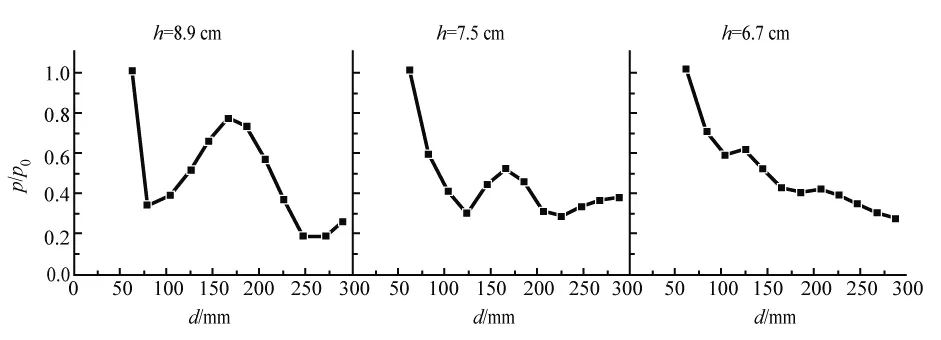
图8 模拟计算对应实验水位下，约化声压极大值p/p0与换能器间距d的关系

3.1 无限大水缸

根据前文分析，水中测声速的异常现象主要来源于水缸侧壁和上下界面的反射，如果令水缸无限大，则本文研究的异常现象应该消失.由于设备限制，在实际实验中无法验证这一推断，但可以通过数值模拟来验证.

扩大换能器中心到侧壁的距离b和到上下界面的距离hu、hd到原来的10倍，使用相同的方法，作接收声压随换能器间距d的变化曲线，如图9所示，可以发现，此时声压的变化模式和空气中的实验现象大致相同，不再出现声压极大值先增后减的异常现象.这一验证表明，水中声速的声压异常变化，确实是由于水与其他介质的界面反射导致的.

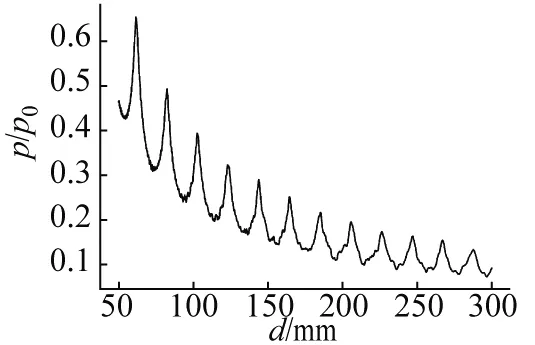
图9 模拟水缸无限大时，接收声压随间距d的变化

3.2 分析评价

本文模型较好地模拟出水中声速测量时的异常现象，但是与实验相比仍有一定误差，这可能是因为截断条件比较粗糙.如果能直接找到叠加函数的收敛形式，比如可以收敛到一个特殊函数上，则结果会更加完备.

现阶段的修正模型是在当前实验条件下的一个较好的近似.数值模拟上，可以通过简单计算，快速得到不同水位下的声压随距离的变化情况(如图9仅需20 s计算时间)，并且可以通过调节介质参数、各界面反射系数等，模拟不同实验条件下的声速测量，甚至可以据此开发一个模拟声速测量的软件，帮助学生更深入地理解实验中的声学现象.

4 结论

本文使用多元高斯声束模型和虚声源模型，解释了水中测量声速时，接收声压极大值随换能器间距非单调变化的异常现象.写出了换能器的接收声压解析表达式，代入实验参数后，模拟计算结果与实验现象较为符合，验证了本方法的合理性.此外，数值模拟了水缸无限大的条件，验证了异常现象消失的推测，进一步证明了水中异常现象的主要来源是水缸侧壁以及上下界面的反射.基于本文的模型，可以进一步开发水中声速测量的模拟软件，通过对水深、介质等参数的便捷调节，向学生展示水中声波的复杂现象，引导学生对理想化模型与实际实验间的差异进行深入思考.