基于t分布随机近邻嵌入的测井数据降维方法研究
2022-05-05邓力珲张俊杰
邓力珲, 曹 丽, 张俊杰
(合肥工业大学 数学学院,安徽 合肥 230601)
测井,也叫地球物理测井,是地质勘查和油气资源评价的一种有效技术手段,它主要利用岩层的电化学特性、导电特性、声学特性、放射性等地球物理特性来测量地质体的地球物理参数特征[1-2]。测井数据隐含着丰富的地质信息,实际工作中需要运用适当的数学物理方法建立相应的测井解释模型,以实现地质体和地质现象由地球物理参数向地质信息的映射转换,如岩性、泥质含量、孔隙度、渗透率等[3-5]。因此,测井数据在地质科学中有着广泛的应用前景[6]。
测井曲线数据是测井资料处理和地质解释工作的重要依据。测井曲线种类众多、数据量大,具有多维、多类、多量、多尺度等显著特征[7]。然而,维度过高必然增加测井解释模型的复杂程度,降低模型的构建及工作效率[8];因此,对测井数据进行降维处理,优选最佳维度及参数,对于提高测井解释工作的效率具有重要意义。根据测井数据从高维空间到低维空间的变换关系,通常可分为线性降维和非线性降维[9-14]。线性降维方法主要包括主成分分析(principal component analysis,PCA)、线性判别分析(linear discriminant analysis,LDA)、独立成分分析(independent components analysis,ICA)等。由于线性降维方法具有计算简便、原理简单、易于解释等特点,在测井数据处理和解释工作中已有一些较好的研究和应用。文献[10]借助PCA进行测井数据降维,并结合K近邻方法对中东Y油田沉积相进行了预测建模;文献[11]运用LDA进行测井数据降维以识别岩性;文献[12]使用ICA与支持向量机(support vector machine,SVM)相结合的方法对沉积相进行定量识别,识别率优于PCA-SVM方法。然而,因为复杂地质作用下的岩体具有非均质性,测井数据的分布往往是非线性的,与地质信息的映射关系亦为复杂的非线性结构,线性降维技术不能保留测井数据的非线性特征,在处理测井数据时存在一定的局限性,所以研究适合测井数据特点的非线性降维方法有利于提高测井数据处理及解释工作的精度和效率。
非线性降维方法主要包括核主成分分析(kernel principal component analysis,KPCA)、等距映射(IsoMap)算法等。文献[13]借助KPCA对煤与瓦斯的特征进行降维,结合概率神经网络对瓦斯突出强度进行识别;文献[14]使用IsoMap作为数据降维方法,结果显示,IsoMap-SVM瓦斯突出预测模型精度高于PCA-SVM模型。上述研究表明,非线性降维方法能够保留复杂数据中的非线性特征,有效地提高了数据处理的质量。但是上述非线性降维方法的可视化程度较低,影响了测井数据的可解释性,从而对后续训练模型的精度产生影响。
t分布随机近邻嵌入(t-distributed stochastic neighbor embedding,t-SNE)算法[15]是一种比PCA更有效的高维数据非线性降维算法,且能通过减少聚集点的生成,提高可视化效果。本文针对测井数据多维度、非线性的特点,引入t-SNE算法对测井数据进行降维处理。以澳大利亚苏拉特盆地Lauren煤层气田测井数据为实验对象,研究基于t-SNE算法的测井数据非线性降维方法及算法实现,并结合SVM,构建t-SNE-SVM岩性解释模型,实现基于测井数据的岩性智能识别。研究结果表明,使用t-SNE降维处理后的测井数据分类明显,保留了原始数据的非线性结构,进而提高了t-SNE-SVM岩性识别模型的透明度和可解释性。
1 t-SNE算法基本原理
t-SNE算法是一种非线性降维技术,该算法是随机近邻嵌入(stochastic neighbor embedding,SNE)算法的改进算法[15-17],主要思想是将高维空间数据点间的欧氏距离转化为联合条件概率,通过计算条件概率的大小来判断数据点的远近程度,进而在低维投影空间重组数据点的空间位置。
假设高维空间中的数据点xi和xj之间的相似性距离用条件概率pj|i表示,计算公式如下:
(1)
其中,σi为以xi为中心的高斯分布的方差。通常最佳σi是借助困惑度Prep,并利用二分法确定的。因此高维空间数据点的联合概率pij可用下式求得,即
(2)
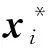
(3)
t-SNE算法通常借助2个分布的KL散度(Kullback-Leibler divergence)确定低维投影空间数据点的相对位置,即计算损失函数C的极值,计算公式为:
(4)
通常利用梯度下降法求取C的最小值,并确定低维投影数据。梯度计算公式为:
(5)
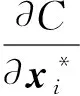
α(t)(X*(t-1)-X*(t-2))
(6)
其中:X*(t)为第t次迭代后的低维样本;η为学习率;α(t)为动量因子。
2 基于t-SNE的测井数据降维算法
2.1 测井数据t-SNE降维基本过程
测井数据降维通常包含数据预处理、数据分析、数据标准化、t-SNE数据降维等过程,如图1所示。
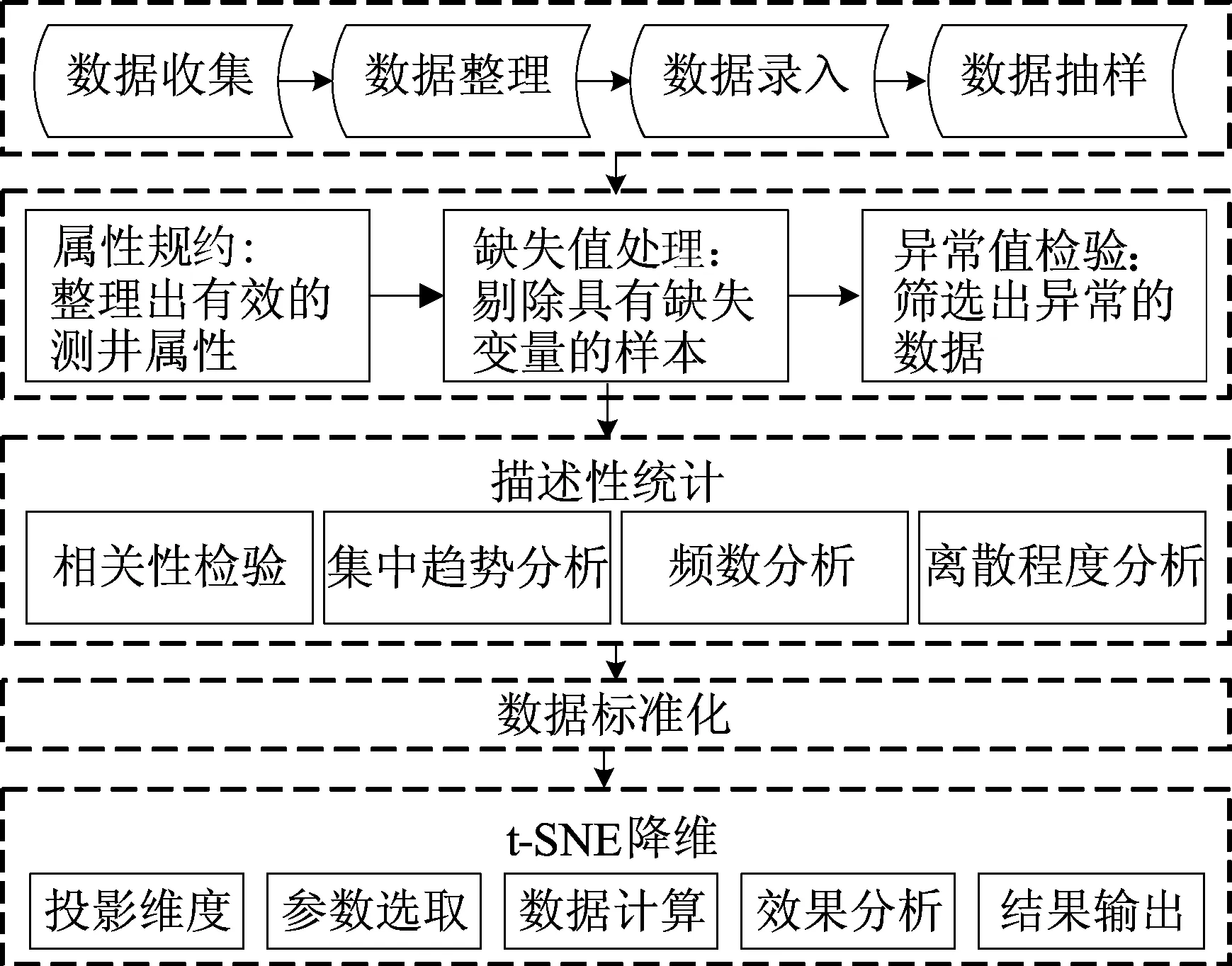
图1 测井数据降维主要工作流程
(1) 数据预处理。因为测量环境、条件及仪器使用不当等主、客观因素影响,测井数据通常存在各种误差,所以首先要对原始数据进行预处理,主要包括:属性规约、缺失值处理和异常值检验等。
(2) 测井数据分析。主要包括相关性检验、集中趋势分析、频数分析和离散程度分析等。
(3) 测井数据标准化。由于不同测井曲线的数值范围存在较大差异,需要对数据进行标准化处理以消除量纲影响,如z-score标准化。
(4) t-SNE测井数据降维。该过程主要包括投影维度确定、参数选取、数据计算等。
2.2 t-SNE测井数据降维算法设计

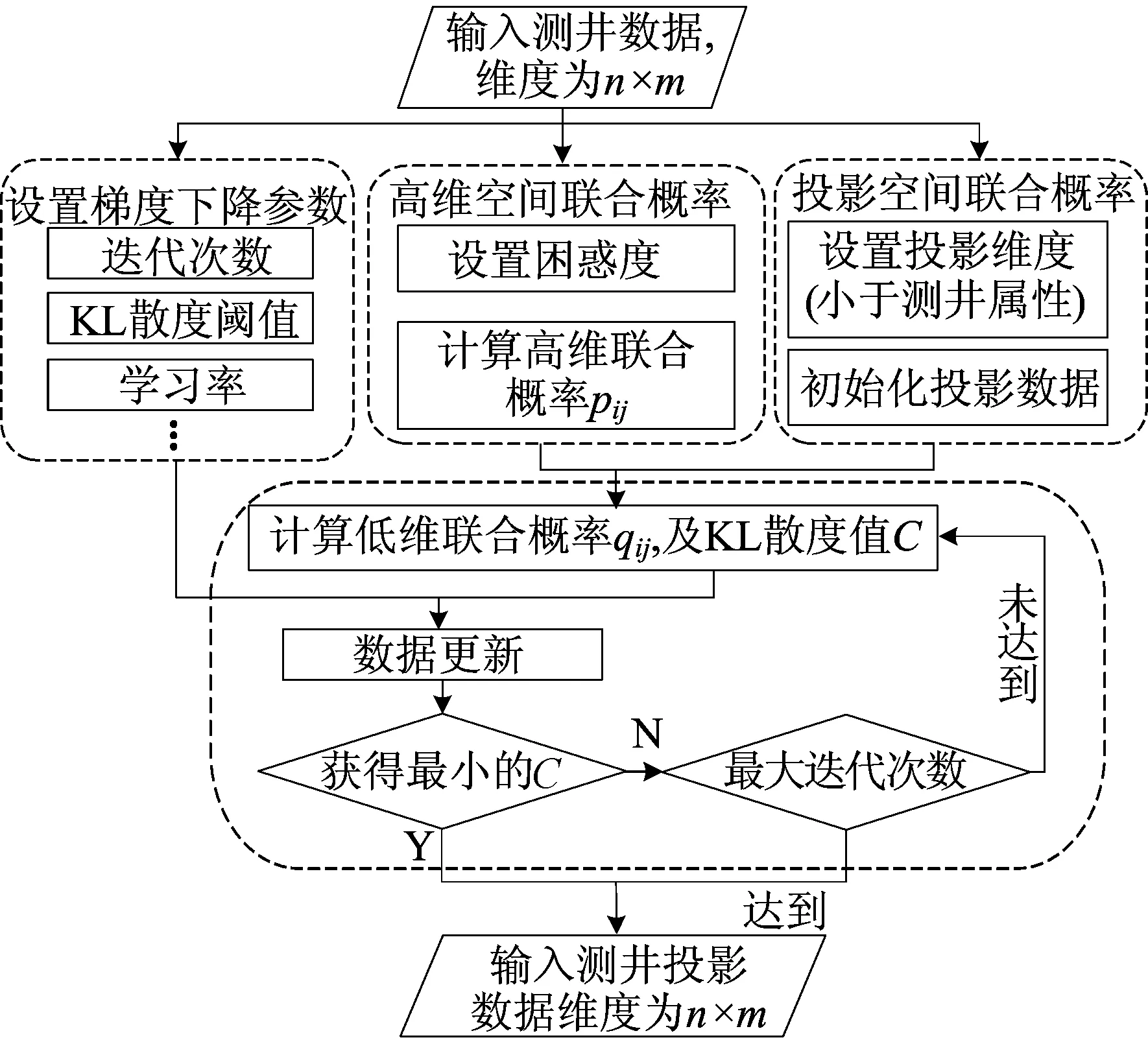
图2 基于t-SNE测井数据降维算法
数据输入:n×m维测井数据。
算法步骤如下:
(1) t-SNE参数初始化。主要包括困惑度Prep、梯度下降最大迭代次数t、学习率η、动量因子α、投影空间维度m′、KL散度C的阈值Cmin等。
(2) 计算高维空间联合概率。通过Prep值计算测井数据方差σi,进而计算测井数据的联合概率pij。
(3) 低维空间投影数据初始化。将每个投影数据随机初始化为m′维向量,将总投影数据记为n×m′的矩阵X*(0)。
(4) 通过最小化KL散度找到最优投影结果。首先使用X*(0)计算低维联合概率qij;然后计算KL散度C(0);最后使用梯度更新规则对投影数据进行迭代更新。若第k次更新后的投影数据为X*(k),迭代次数k>t或C(k) 本文以澳大利亚苏拉特盆地Lauren煤层气田测井数据为例,进行基于t-SNE算法的测井数据降维研究,实现复杂高维测井数据的非线性智能降维。 根据测井原始数据特点,经属性规约、缺失值处理、异常值检验等预处理过程,整理出与测井解释高度相关的测井曲线,用于t-SNE降维算法研究。主要包括自然伽马GR、补偿密度DEN、井径CAL、浅电阻率RS、深电阻率RD等11个维度。 测井曲线数据分布统计结果见表1所列。 表1 测井曲线数据分布统计结果 此外,在测井数据预处理过程中,还得到岩性学习样本348个。由表1可知,这些测井曲线数据存在数据离散及波动程度较大等问题,需要进行标准化处理,以消除量纲影响,提高数据质量和精度,其标准化公式为: (7) 其中:μi表示xij的均值;σi表示xij的标准差。经过标准化,测井数据的分布情况比较稳定,如图3所示。 图3 测井数据标准化结果箱线图 根据t-SNE原理可知,影响最终结果的主要参数包括投影维度、困惑度等。先对相关参数进行确定;为了确定最优参数,以KL散度作为衡量指标,KL散度越小,说明降维效果越好。因为困惑度与投影维度间存在相互影响关系,所以使用穷举法优选最佳参数。 首先,通过固定困惑度,计算投影维度1~11间的KL散度值。经对比分析,投影维度为2时,KL散度最小,且投影维度增大,KL散度逐步增大,如图4a所示;依据优选的投影维度,将困惑度的范围限定为5~50[13],计算KL散度值,如图4b所示。可以看出随着困惑度增大,KL散度呈波状递增,确定最佳困惑度为5。 图4 KL散度趋势 最后,利用梯度下降法对X*进行迭代运算,输出结果即为低维空间的投影数据。 传统的线性降维方法PCA在低维空间的主元相互独立,这就导致在高维空间中不相关,但距离很近的数据点在低维空间可能会相距较远。但是在t-SNE算法中,投影样本的相关系数不需要为0,因此能够在低维空间中保持高维空间中数据的近邻关系,使得同簇的样本更加邻近,不同簇的样本相互远离,保留了原始数据的局部结构特征。因此,从数据可视化角度来看,t-SNE算法具有更好的可视化效果,如图5所示。 图5 t-SNE和PCA投影 SVM是机器学习中最流行的模型之一,能够执行线性或非线性分类,应用十分广泛。下面将本文的t-SNE-SVM岩性识别模型和PCA-SVM岩性识别模型进行对比分析。在对测井数据预处理和降维后,确定SVM模型输入维度为2,输出类别为3类,并且通过测试训练确定模型核函数为径向基核函数(radial basis function,RBF),惩罚系数为1,最终t-SNE-SVM模型结果见表2所列。结果表明,模型训练精度为92.53%,砂岩判断准确率为93.53%,砂泥岩判断准确率为90.23%。PCA-SVM模型最终结果见表3所列,模型训练精度为86.49%,砂岩判断准确率为86.57%,砂泥岩判断准确率为83.24%。 表2 t-SNE-SVM岩性识别模型训练精度 表3 PCA-SVM岩性识别分类结果 针对测井数据维度高、结构复杂等特点,本文提出使用非线性降维方法t-SNE对测井数据进行降维处理,构建了t-SNE-SVM岩性识别模型,并与PCA-SVM岩性识别模型进行了对比;同时从可视化角度、模型训练精度和岩性判断准确率等方面和传统线性降维方法PCA进行对比分析。结果表明,t-SNE-SVM岩性识别模型精度更高,可解释性更强。因此将非线性降维方法t-SNE应用于测井数据的降维对后续测井数据的相关定量评价分析具有一定的参考价值。3 基于t-SNE的测井数据降维
3.1 测井数据预处理
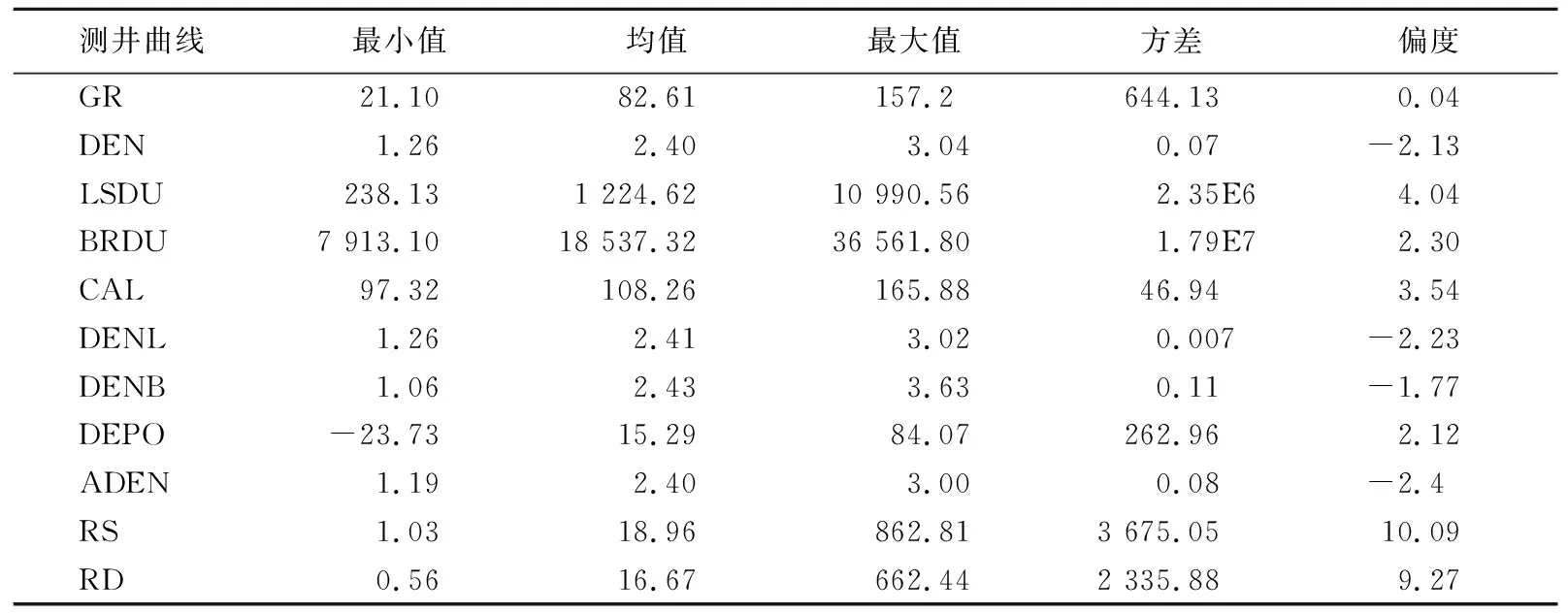
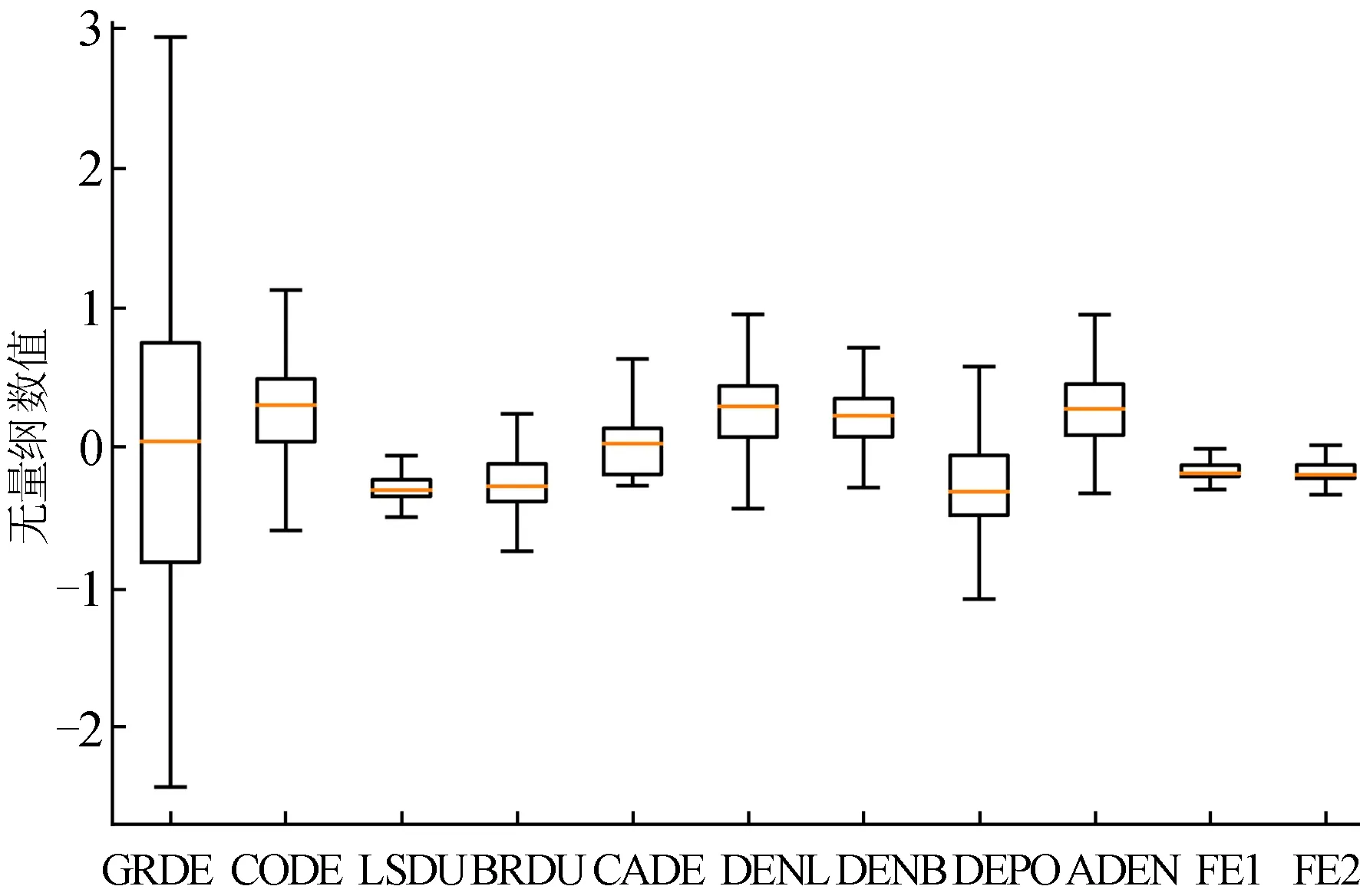
3.2 基于t-SNE的测井数据降维
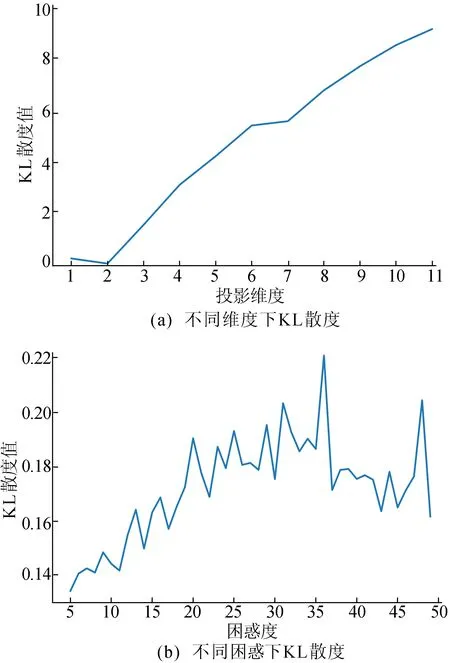
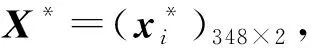
4 t-SNE测井数据降维效果分析
4.1 t-SNE与PCA可视化效果对比
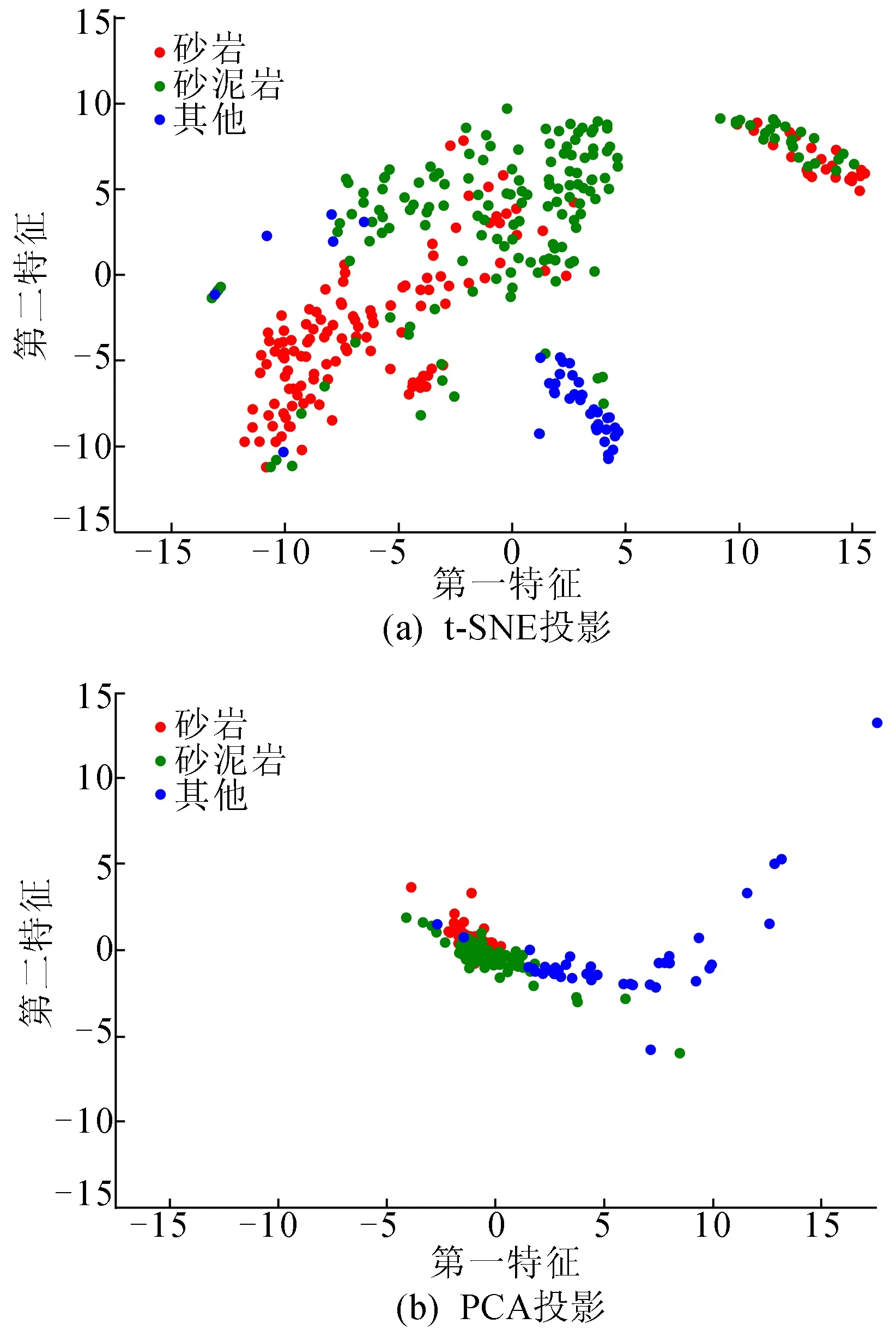
4.2 t-SNE-SVM和PCA-SVM效果对比
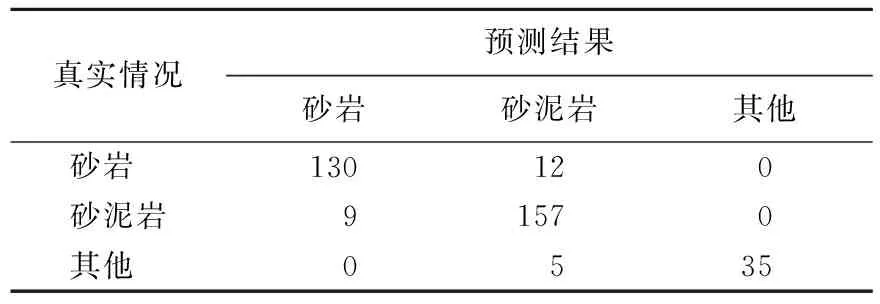
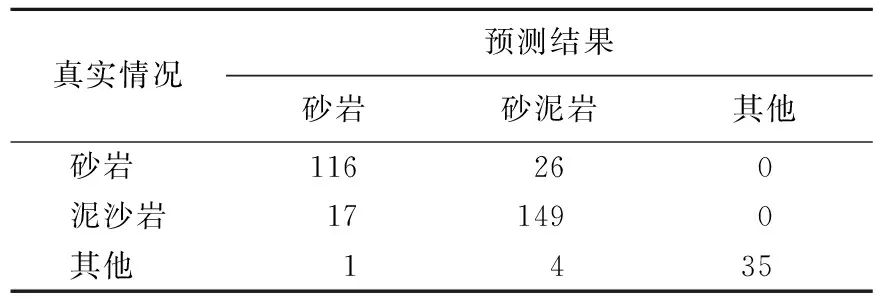
5 结 论
