根式基础极限承载力预测的修正双曲线法

沈浩浩, 罗晓光, 余 竹

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.安徽省交通控股集团有限公司,安徽 合肥 230088)

0 引 言

根式基础或根桩是一种新型基础形式[1],它是通过将预制的根键顶入桩身预留的孔中而形成的一种异形桩,因形似树根而得名,已成功应用于马鞍山长江大桥、池州长江公路大桥中。根式基础通过顶入根键来提高承载力并减小沉降,充分发挥根键的作用,现场试桩的荷载试验表明效果显著,具有很好的应用前景。

根式基础竖向和水平承载力研究已经取得一些成果[2-3]。桩-土相互作用的机理较为复杂,引入水平的根键后更难处理,具有较大的不确定性,因此现场载荷试验的结果是确定根式基础承载力的最可靠方法[4]。然而由于现场静载试验费用大,受制于现场条件可能无法加载到根式基础破坏就停止加载,很难得到根式基础的最终极限承载力。从已有的试桩资料统计来看,一些根式基础的试桩结果未达到相应规范要求的极限承载力,因此如何通过已有的试桩数据准确预测根式基础的极限承载力是当前需要考虑的问题[5-6]。

为了解决普通桩的极限承载力预测问题,文献[7]采用双曲线模型模拟桩的荷载-沉降曲线,预测单桩的承载力;文献[8]采用完整指数模型拟合单桩荷载-沉降曲线;文献[9-10]利用完整指数模型等数学模型,估算试桩未达破坏时的单桩极限承载力;文献[11]对比分析了几种单桩竖向极限承载力的预测模型;文献[12-13]分别提出基于Boltzmann函数及Usher生长模型的单桩极限承载力预测模型。

本文在普通桩极限承载力预测的双曲线模型基础上,结合根式基础的特点,即考虑根键的作用,提出一种修正双曲线模型,能够更好拟合根式基础的荷载-沉降(Q-s)曲线;进行根式基础的极限承载力预测,并与完整指数模型及现场试桩实测结果进行对比分析,验证所提出修正双曲线模型预测根式基础极限承载力的有效性。

1 根式基础承载力预测模型

1.1 修正的双曲线模型

传统的双曲线模型和完整指数模型可以用来描述桩顶Q-s关系,能基本拟合桩基静荷载的Q-s曲线。

双曲线模型假设桩基础的Q-s曲线符合双曲线方程,即

(1)

其中:Q为作用于桩顶的荷载;s为桩顶沉降量;a为Q-s曲线原点的切线斜率的倒数;b为基础极限承载力的倒数。

完整指数模型假设桩基础的Q-s曲线符合指数方程,即

Q=Qu(1-e-b′s)

(2)

其中:Qu为基础的极限承载力;b′为经验参数。

为了更好地模拟实际工程的情况,一些研究者对双曲线模型作出相应的修正。文献[14]在预估试桩极限承载力时提出调整双曲线模型;文献[15]在研究嵌岩预应力高强混凝土(prestressed high-intensity concrete,PHC)管桩承载特性时提出修正双曲线模型;文献[16]在描述抗拔挤扩支盘桩Q-s曲线时提出相应的修正双曲线模型。

大量工程实践证明,传统的双曲线模型在桩基的弹性变形阶段能够很好地拟合Q-s关系,但是当荷载水平较高时,进入塑性变形阶段后拟合效果并不是很理想,导致拟合的Q-s曲线尾部误差较大,最终的单桩极限承载力预估值与现场实测值产生偏差。

针对根式基础的特性,为了体现根键对于极限承载力的影响,提高拟合精度,考虑到双曲线模型应用的广泛性,本文在双曲线模型的基础上建立如下修正的双曲线模型:

(3)

其中,分母增加ce-ds这一影响因子,即引入新的c、d经验参数,使得该模型能够更好地拟合根式基础Q-s曲线。可以看出,当c=0时,(3)式为普通的双曲线模型,为本文修正模型的一个特例。

该修正模型用于调整桩顶Q-s曲线弹性变形阶段和弹塑性变形阶段,应同时满足双曲线模型的2个明显特征:当s取值为0时,Q取值为0;当s→∞时,Q=Qu。因此,(3)式中需要d>0,c没有特定的要求,拟合时无取值限制。

1.2 模型参数确定

对于修正的双曲线模型(3)式,只要求得模型中的参数a、b、c、d,即可进行根式基础极限承载力预测。根据根式基础现场载荷试验的试桩资料,可获得一系列的桩顶荷载Qi与相应的竖向沉降si(i=1,2,3,…,m;m为荷载施加级数)。只需对Q-s曲线进行非线性拟合,即可得出这些参数的取值。

为了保证实测的桩顶荷载Qi与拟合的桩顶荷载Qi′总体偏离度最小,保证偏差的均值达到最小,取目标函数为:

(4)

其中,Δ为相对误差。采用最小二乘法非线性拟合桩顶Q-s曲线,可以找到使目标函数取得最小值时相应的参数。

最小二乘法非线性拟合采用Levenberg-Marquardt算法,该算法是对Gauss-Newton算法的一种改进,利用如下线性方程组的解dk作为在点xk处的一个搜索方向:

(J(xk)TJ(xk)+μkI)dk=-J(xk)TF(xk)

(5)

dk=-(J(xk)TJ(xk)+μkI)-1J(xk)-1F(xk)

(6)

其中:k为迭代次数;I为单位矩阵。为书写方便,下文将J(xk)、F(xk)分别简记为Jk、Fk。

Fk=[F1(x)F2(x) …Fn(x)]，F1,F2,…,Fn均为(x1,x2,…,xn)上的多元函数,Jk为Fk的Jacobi矩阵。Fk和Jk矩阵维度应根据实测荷载级数确定,本文采用信赖域的方法,引入参数μk>0,克服Jacobi矩阵奇异所带来的搜索困难,从而获得全局收敛的解。μk计算公式为:

(7)

其中,θ为给定参数,0<θ<1;αk为调整因子,迭代过程中通过不断调整其大小来改变参数μk的大小,(5)式的解与参数μk相关。

该算法迭代过程如下:

(1) 给定x1∈Rn,ε≥0,α1>q>0,0≤p0≤p1≤p2<1,k∶=1。其中:q为给定参数,是αk的下界,当迭代解靠近方程组真实解时,防止试探步过大引起的数值计算困难;p0、p1、p2为给定参数,按照信赖域方法的普遍做法,取p0=0.000 1,p1=0.25,p2=0.75,迭代过程中其大小不变。

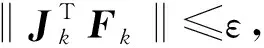
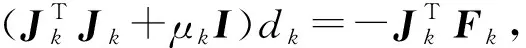
(3) 定义第k步实际下降量Adk和预估下降量Pdk分别为:

Adk=‖Fk‖2-‖F(xk+dk)‖2,

Pdk=‖Fk‖2-‖Fk+Jkdk‖2。

计算rk=Adk/Pdk,通过rk来判断试探步dk是否可以接受,并调整每次迭代过程中参数μk的取值。令

(4) 计算αk+1,即

令k∶=k+1,返回步骤(2)继续迭代。

2 工程实例验证

对池州长江公路大桥(简称“池州桥”)、秋浦河特大桥(简称“秋浦河桥”)、淮河特大桥(简称“淮河桥”)、望东长江公路大桥(简称“望东桥”)工程中共计5根根式基础现场荷载试验结果进行模拟和验证。池州桥有2根试桩,其中1根试桩采用堆载法进行加载,其余4根试桩均采用自平衡法进行加载,在试桩下部位置埋设一个大型荷载箱,桩身埋设测试元件,待桩身砼龄期达到测试要求后进行加载。

池州桥覆盖地层第1层至第8层为第四系全新统冲积层,下伏基岩为白垩系下统杨柳湾组泥质粉砂岩、砂岩和粉砂质泥岩。

淮河桥地表出露地层为第四系全新统、上更新统,其下伏基岩为上太古界霍邱群、上寒武统、下奥陶统、二叠系、白垩系、下第三系。

望东桥覆盖地层主要由第四系冲积成因的黏性土、粉细砂及卵石、碎石土组成,下伏基岩为第三系双塔寺组砾岩、二叠系灰岩。

秋浦河桥下伏基岩以白垩系上统宣南组砾岩为主,局部夹透镜体状泥质粉砂岩,岩面平缓,上部砾岩胶结程度相对较弱,下部砾岩胶结较好。5根根式基础的试桩详细参数见表1所列。

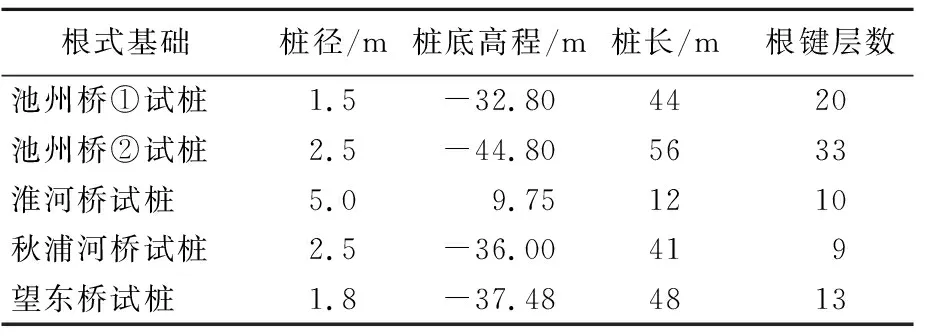
表1 根式基础试桩参数

为了比较分析,5根根式基础分别采用传统双曲线模型、完整指数模型和本文修正双曲线模型3种模型进行Q-s曲线拟合,拟合结果如图1～图5所示,并与实测数据进行比较。从图1～图5可以看出,本文修正双曲线模型能够更好地拟合根式基础的Q-s曲线,主要体现在曲线的尾部。当荷载等级较低时,3种模型均能较好地拟合根式基础的承载特性,但当荷载逐渐增大直至停止加载,双曲线模型和指数模型的拟合曲线都出现一定程度的偏离,没有很好地体现根式基础的极限承载力,而本文修正双曲线模型可以更好地拟合根式基础Q-s曲线,与实测数据较为相符,其预测的根式基础极限承载力也具有更高的可信度。

5根根式基础拟合的相关系数见表2所列。从表2可以看出,本文修正双曲线模型的拟合效果均好于双曲线模型和完整指数模型,相关系数(R)达到0.995 4以上,平均为0.998 5,高于双曲线模型的0.992 0和指数模型的0.996 7。

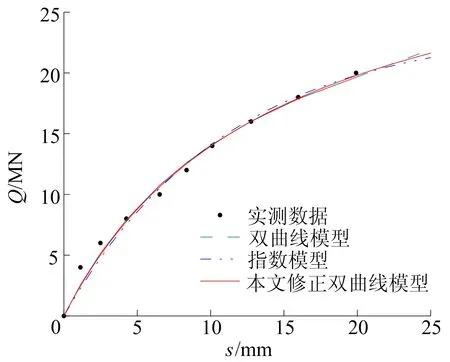
图1 池州桥①试桩拟合结果

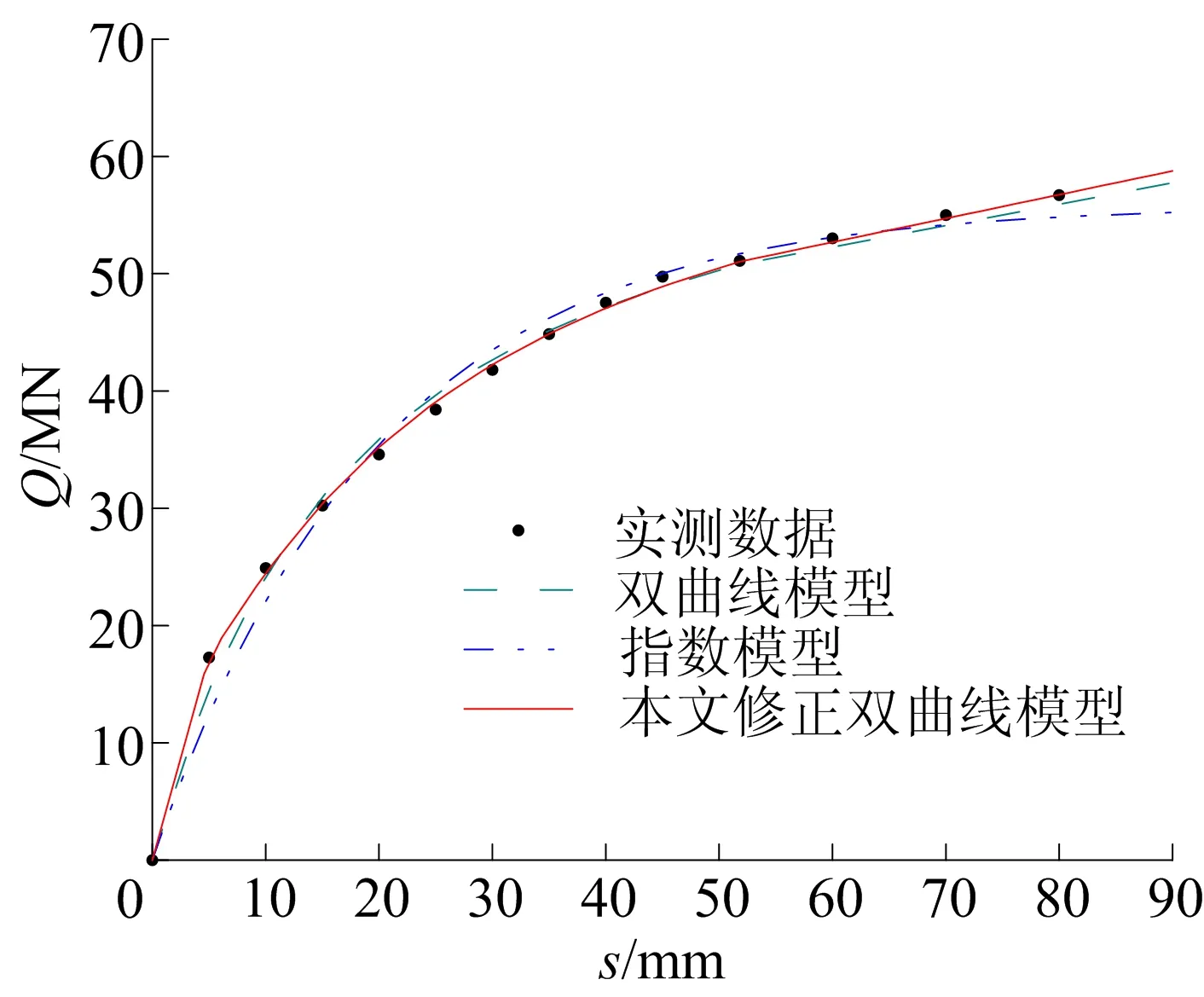
图2 池州桥②试桩拟合结果

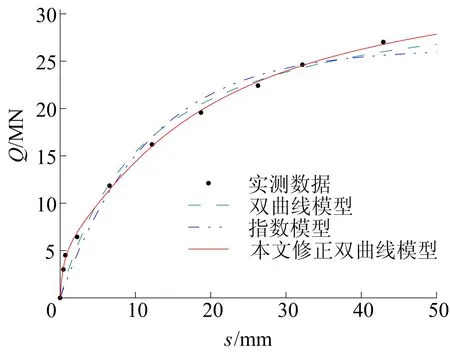
图3 淮河桥试桩拟合结果

图4 秋浦河桥试桩拟合结果

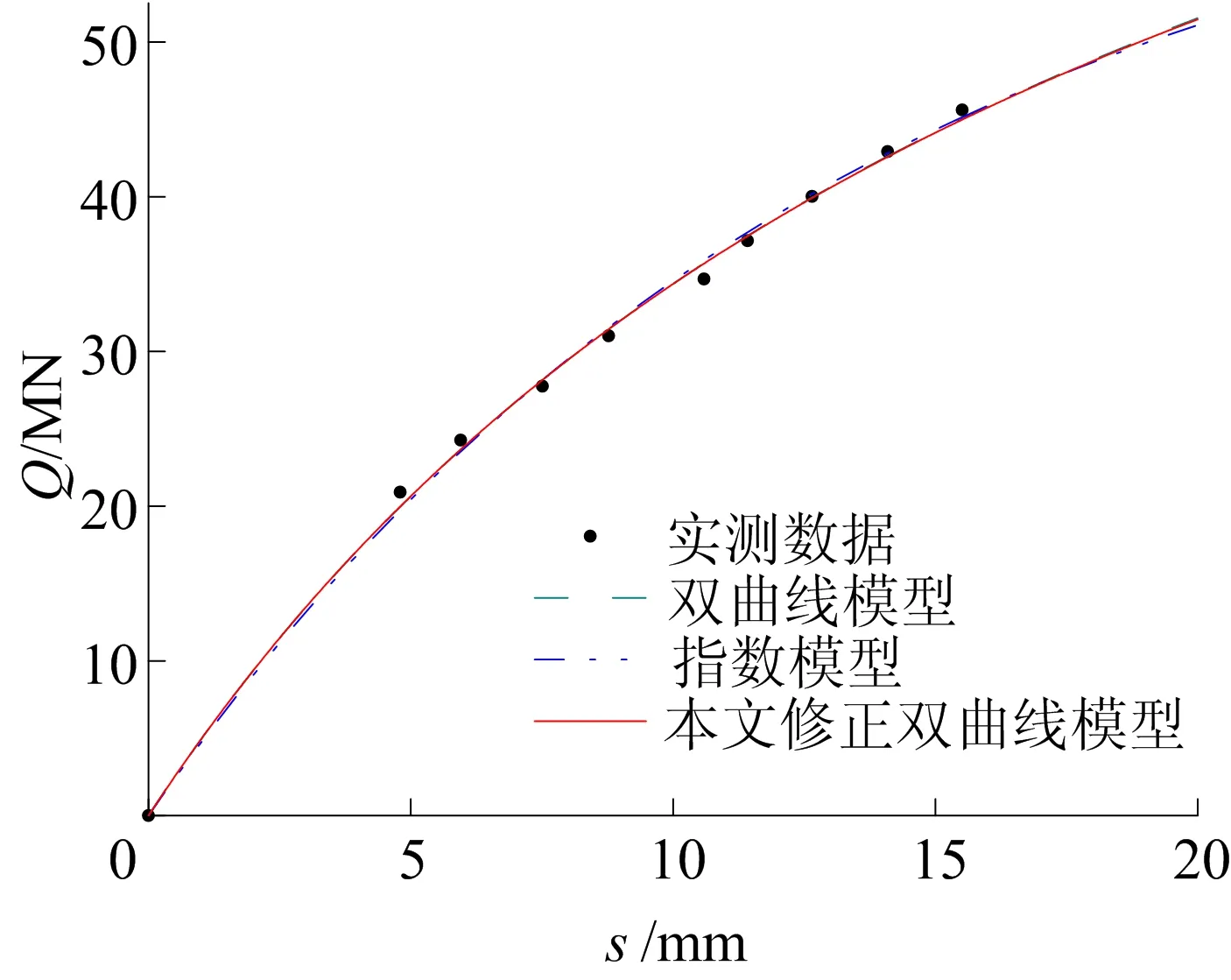
图5 望东桥试桩拟合结果

以淮河桥试桩(R=0.998 4)拟合曲线为例,对各级荷载的拟合值进行验证,结果见表3所列。从表3可以看出,淮河桥试桩各级荷载最大相对误差为3.547 3%,平均相对误差为1.789 9%,拟合效果很好,在荷载等级较高时相对误差均较小,对曲线尾部拟合精度较高,能够很好地描述荷载等级较高时根式基础的承载特性。

以池州桥②试桩(R=0.995 4)为例进行拟合曲线的验证,取前10级荷载进行曲线拟合,得到相应的拟合参数后,通过拟合曲线对最后3级承载力进行预测,并与实测值对比,结果见表4所列。由表4可知,池州桥②试桩最后3级荷载的实测值与预测值非常接近,平均相对误差为0.756 5%,拟合曲线的结果具有较高的可信度,可用来进行根式基础极限承载力预测。

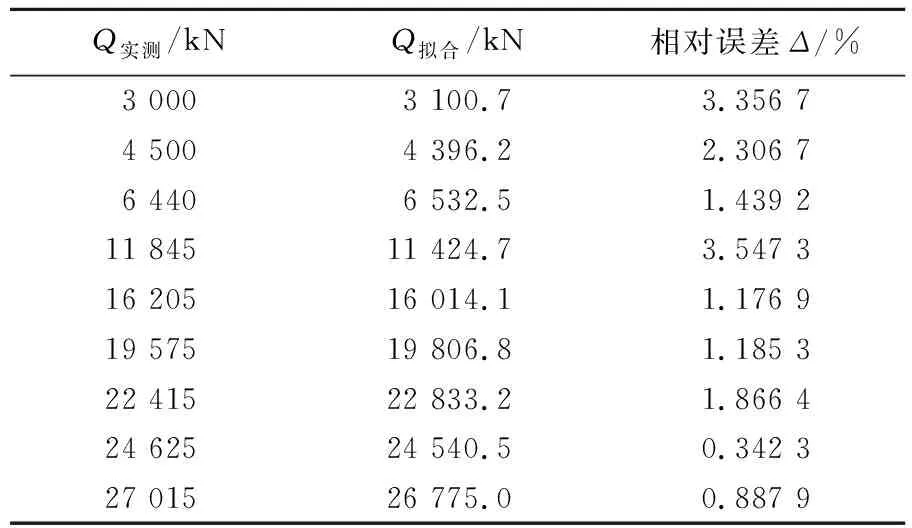
表3 淮河桥试桩拟合值验证

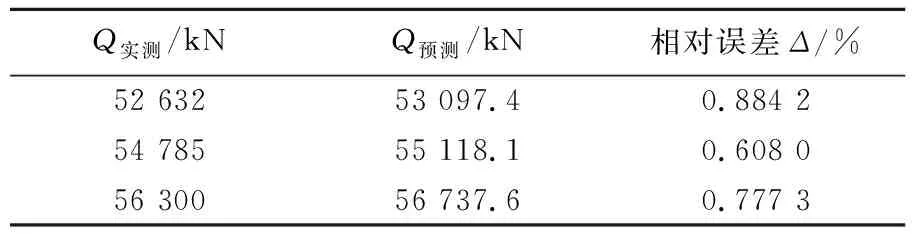
表4 池州桥②试桩最后3级荷载预测值验证

3 根式基础极限承载力预测

根据文献[17],试桩极限承载力的确定主要有以下方式:对于陡降型Q-s曲线,取其发生明显陡降的起始点对应的荷载值;对于缓变型Q-s曲线可根据沉降量确定,宜取s=40 mm对应的荷载;对于直径大于或等于800 mm的灌注桩或闭口桩,可取s=0.05D对应的荷载值。

根式基础由于根键的存在大大提升了承载力和抗变形能力,Q-s曲线均表现为缓变型,确定承载力时要考虑土体结构对基桩沉降的要求。当Q-s曲线呈缓变型且桩长超过40 m时,可加载至桩顶总沉降超过80 mm,故根式基础采用80 mm与0.05D中的较小值对应的荷载值为相应的极限承载力。根式基础的极限承载力现场实测结果和本文修正双曲线模型预测结果对比见表5所列。

从表5可以看出,根式基础的预测极限承载力均高于现场实测的承载力,这是由于受到现场加载条件的限制,现场试验均无法加载到根式基础破坏。对于采用自平衡法测试的根式基础,上段桩先于下段桩达到试验终止的条件,未得到下段桩的极限承载力。

望东桥试桩由于桩底嵌岩,且桩身进行了注浆,极限承载力较大,受限于加载条件,达到荷载箱最大加载能力时,根式基础的沉降仅有15 mm,远没有达到文献[17]要求的极限值,因此极限承载力远远超出现场实测值。

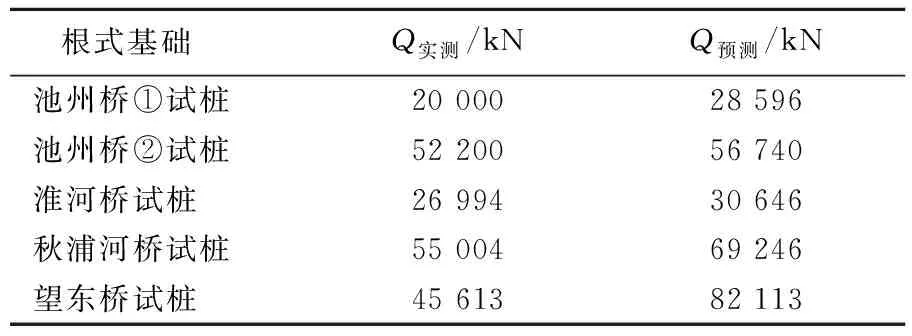
表5 根式基础极限承载力预测结果与实测结果对比

4 结 论

根式基础是一种新型的桩基础,本文提出修正的双曲线模型预测根式基础的极限承载力,并与传统模型和实测结果进行比较,得到以下结论:

(1) 传统的双曲线模型、完整指数模型和本文修正双曲线模型对根式基础的拟合表明,本文修正双曲线模型具有更高的拟合精度,拟合效果更好,相关系数均在0.995 4之上,平均相关系数为0.998 5。

(2) 基于本文修正双曲线模型的根式基础荷载的计算值与实测值之间的误差较小,且曲线尾部与实测结果吻合更好,拟合精度更高,表明本文修正双曲线模型可用来预测根式基础的极限承载力。

(3) 从承载力预测结果可以看出,根键的存在大大提高了根式基础的竖向极限承载力,受到现场试桩条件的限制,根式基础现场实测极限承载力过于保守,按照现场实测极限承载力进行设计具有很高的安全系数。