基于非结构化数据的LLE-WOA-LSSVR碳价格组合预测模型
2022-05-05周熠烜陈华友周礼刚朱家明
周熠烜, 陈华友, 周礼刚, 朱家明
(1.安徽大学 数学科学学院,安徽 合肥 230601; 2.安徽大学 互联网学院,安徽 合肥 230039)
0 引 言
在控制全球变暖的过程中,减少碳排放是至关重要的环节和有效途径。为了控制二氧化碳的排放,全球碳交易市场应运而生。碳交易有利于合理地对碳配额进行分配,进而减缓全球变暖的进程。因此,如何有效预测碳价格是学术界需要解决的重要而迫切的研究课题。
传统的组合预测模型使用的数据大多来源于政府或相关统计部门,这些数据为年度统计数据,并有一定的滞后期,此类数据为类型单一的结构化数据。然而在网络环境下,搜索引擎的使用越来越频繁,从而导致非结构化数据广泛存在,因此有必要探讨非结构化数据所提供的有效信息来提高预测的准确度。
实际上,百度指数就是一类重要的非结构化数据。它以关键词的搜索次数为基础,科学地分析计算各关键词在百度搜索中的加权和,进而揭示大众关注对信息的影响机制[1]。文献[2]利用格兰杰因果关系检验分析实际游客流量和网络搜索量之间的联系,构建了基于百度指数的故宫游客流量预测模型;文献[3]利用百度指数衡量用户关注度,探究普通投资者的关注程度对股票流动性及股票收益可能造成的影响。
近年来,人工智能算法得到了很大程度的发展,相比较传统的组合预测方法具有更高的鲁棒性和精确性。因此结合人工智能算法构建组合预测模型能提高容错率,挖掘数据中的潜在信息,提高预测精准度。文献[4]应用改进的v-支持向量回归(v-support vector regression,v-SVR)模型预测股票价格;文献[5]采用粒子群优化算法改进支持向量机模型,并用改进后的模型进行房价预测;文献[6]运用神经网络集成学习方法建立模型对股票市场进行预测;文献[7]运用非线性自回归神经网络(nonlinear autoregressive neural network,NANN)对大气密度进行了预测;文献[8]应用最小二乘支持向量机(leasts squares support vector machine,LSSVM)方法对太阳黑子进行预测,并对模型中的参数进行优化,取得了很好效果。
国内外对碳市场价格的分析与研究一直是学术界关注的热点问题之一[9],国内外学者提出了多种方法实现对碳价格的预测。文献[10]考虑灰色理论的特点,利用带有残差修正的GM(1,1)结果优化模型对碳交易试点的价格进行预测;文献[11]结合灰色预测方法和马尔科夫理论,使用改进的Grey-Markov模型对碳价格的波动进行预测;文献[12]应用差分整合移动平均自回归模型(autoregressive integrated moving average model,ARIMA)模型和LSSVM组合模型预测国际交易市场的碳交易价格;文献[13]针对焦炭消费的特点,构建了带BP神经网络的半参数组合预测模型。实验表明上述模型具有较高的预测精度。
然而,上述有关碳价格预测模型利用的数据均是结构化数据,并没有考虑非结构化数据对碳价格的影响。因此,目前的碳价格预测若采用传统的组合预测模型,则存在一定的缺陷。具体表现为传统的组合预测模型大多对单项预测结果进行线性的加权平均获得预测结果,因此预测精度过分依赖于单项预测模型的选择。例如,假设某个指标的实际值为100,而3种单项预测结果均大于110,因此线性加权算术平均导致组合预测的结果也至少是110以上,从而造成较大的误差。实际上,碳价格预测考虑到非结构化数据的影响,在混合数据结构下碳价格和影响因素呈现非线性数据特征,这是传统的组合预测方法所不能反映的。本文所构建的基于局部线性嵌入和鲸鱼优化算法的最小二乘支持向量回归(locally linear embedding-whale optimization algorithm-least squares support vector regression,LLE-WOA-LSSVR)预测模型改变了传统的组合预测模型的思路,把组合预测看成是一个预测过程。先考虑对众多的非结构化数据进行降维处理,提取出数据有效信息特征,降低一些次要的或偶然因素对系统行为扰动的影响。在此基础上,利用机器学习算法LSSVR进行非线性建模,并对模型的参数利用鲸鱼算法(whale optimization algorithm,WOA)进行优化,从而进一步改进传统的组合预测方法。
为此,本文在现有文献基础上,构建新的基于非结构化数据的LLE-WOA-LSSVR碳价格组合预测模型。该模型具有如下创新性:
(1) 为了克服结构化数据包含信息的不全面性,本文考虑非结构化数据对碳价格的影响,调查碳价格相关关键词的百度指数,并运用局部线性嵌入(locally linear embedding,LLE)算法对数据进行降维。
(2) 利用WOA算法优化LSSVR模型中的参数,并利用优化后的模型对碳价格数据进行训练、测试和预测。
(3) 通过比较4种不同预测方法的碳价格预测结果。实例分析表明,本文提出的组合预测模型合理且有效。
1 非结构化数据与单项模型基本原理
1.1 非结构化数据
非结构化数据是指数据结构不规则或不完整,没有预先定义的数据。相比较结构化数据,非结构化数据隐藏着很多重要的信息,引入非结构化数据,可以完善数据提供的信息,使得信息更加全面,有利于获得更加精准的预测结果。
本文利用百度指数作为非结构化数据来源,通过相关关键词在百度的每日搜索量,分析并预测未来碳价格的变化趋势。假设样本集X={X1,X2,…,Xn}为影响碳价格影响因素的指标集合。
1.2 LLE算法
LLE算法是文献[14]提出的一种流行的学习非线性降维方法。该方法假设高维空间内的样本点在局部内的关系是线性的,即一个样本点可以由若干个相邻的点来线性表示。通过LLE算法降维后,样本点集合在低维空间中仍保持这样的线性关系不变。
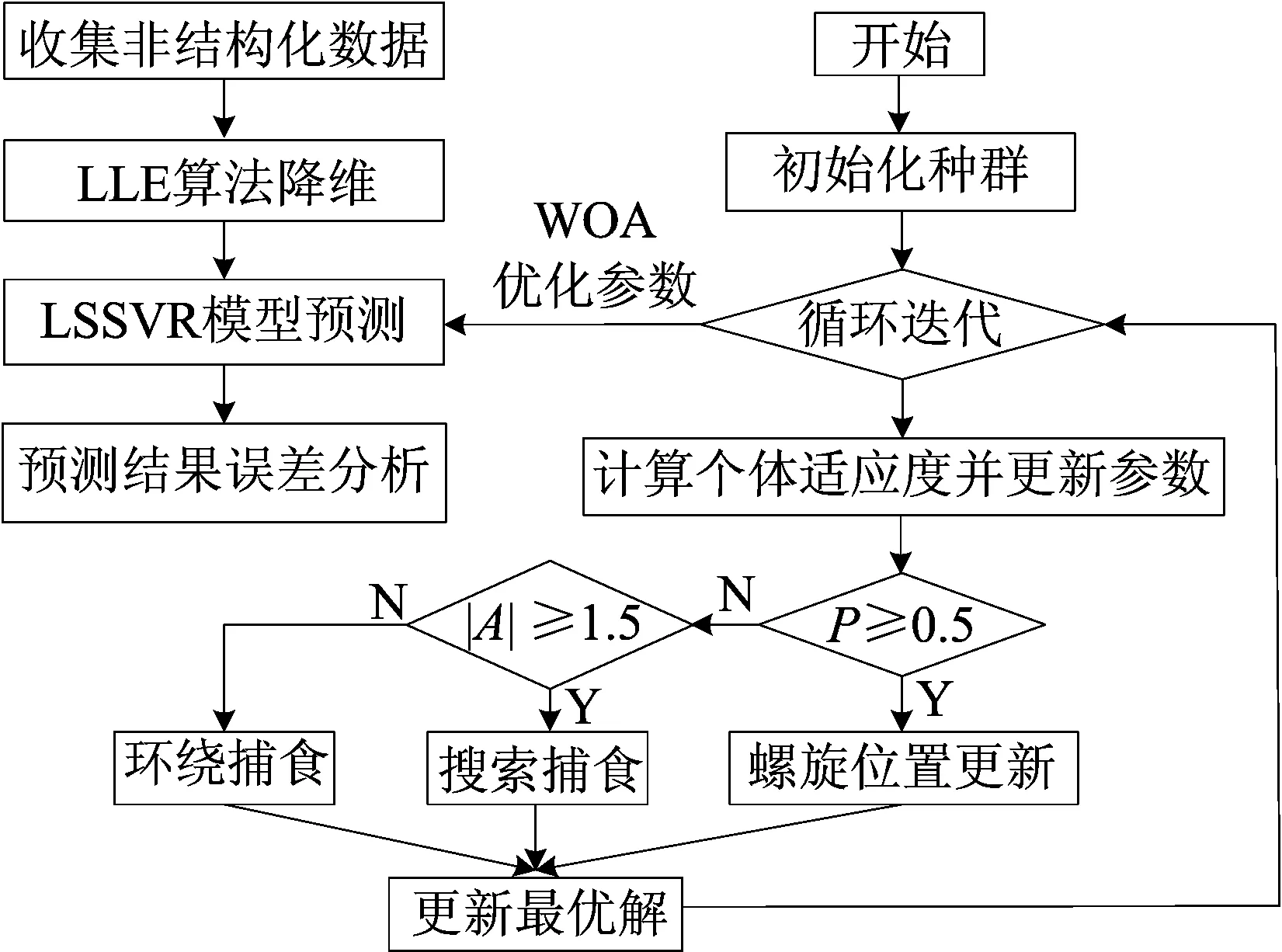
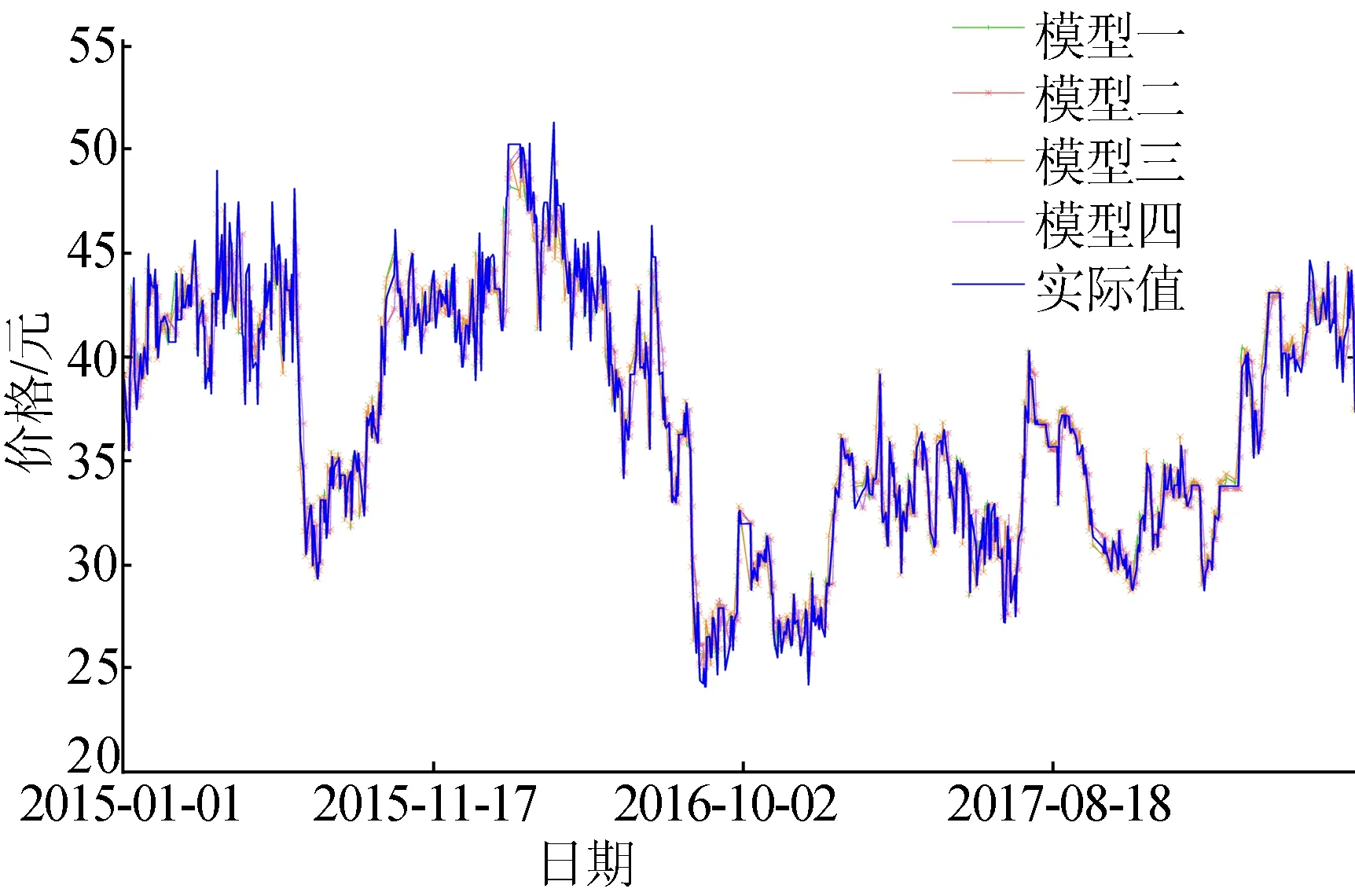
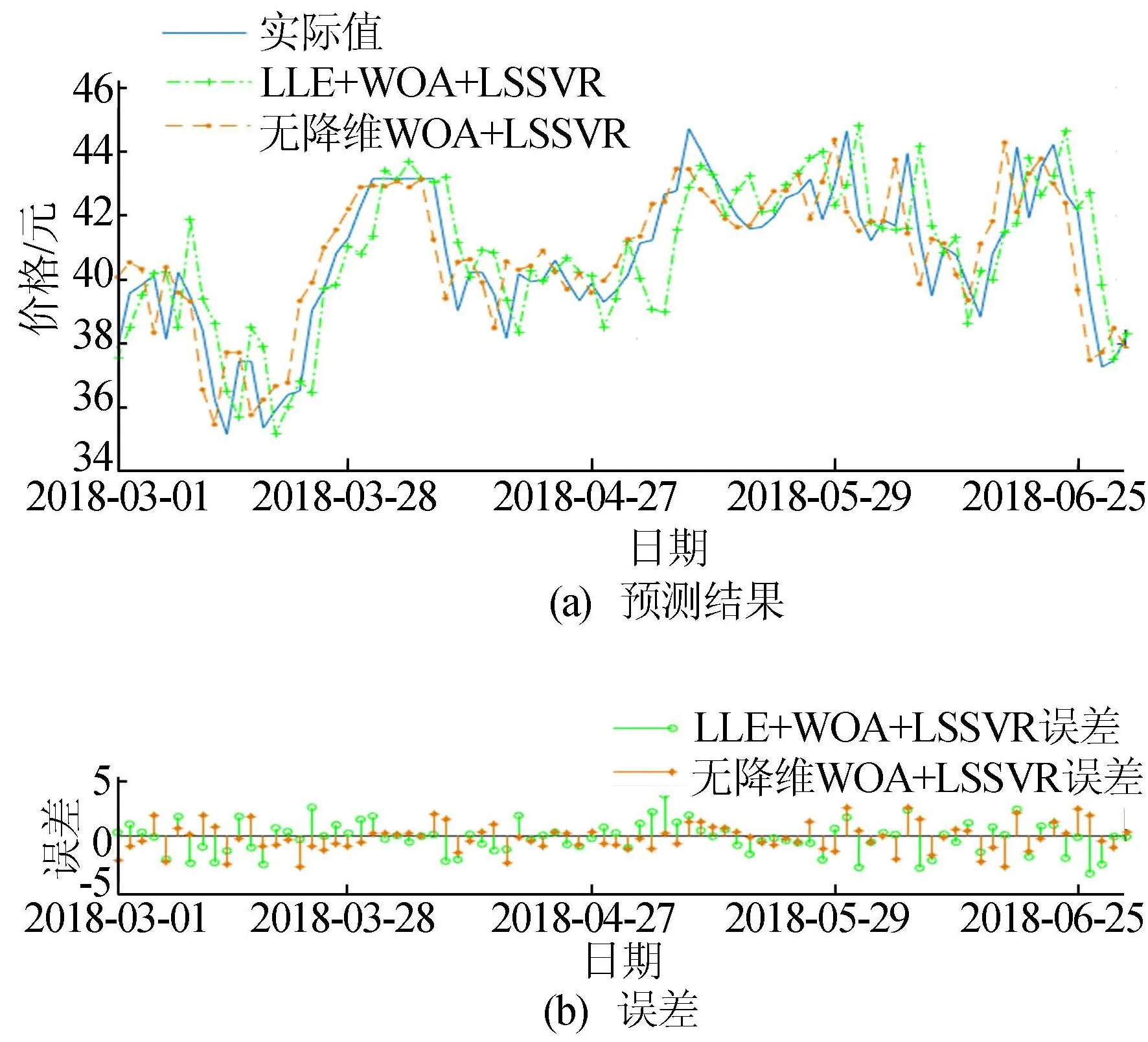
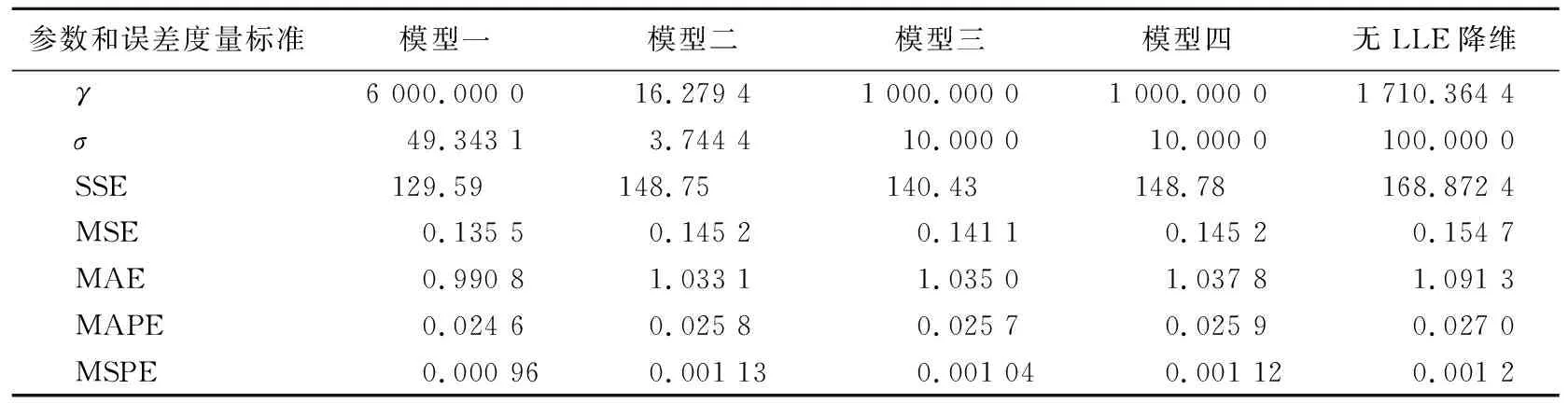
LLE算法基本思想是将高维样本数据集X={X1,X2,…,Xn}(Xi∈Rd)映射到低维样本数据集Y={Y1,Y2,…,Yn}(Yi∈Rd′),其中维数d′ (1) 对于高维空间的样本集X={X1,X2,…,Xn}中的元素,计算每个样本点Xi和剩余的n-1个样本点之间的欧式距离dij=|Xi-Xj|。按距离从小到大进行排序,选择前K个距离Xi最近的样本点作为xi的近邻点集合Qi。 (1) (2) LSSVR是文献[15]对支持向量回归的改进,在标准算法的基础上将最小二乘估计引入SVR算法中,通过把原算法中的不等式约束转化为等式约束,对二次线性规划问题的求解转变为对线性方程组的求解,可以极大地减少运算量,提高运算效率。在原始的低维空间中,线性回归的问题可以由如下线性方程表示: f(x)=ωTx+b (3) 其中:ω为权重向量;b为偏差。在选用合适的核函数映射到高维特征空间后,线性回归的问题可以由下式表示: y=ωTφ(x)+b (4) 其中,φ(x)为非线性变换。和SVM算法相类似,根据结构风险最小化原则,LSSVR算法的优化目标函数可以表示为: (5) 其中:ei为误差;γ为惩罚系数。 (5)式是一个等式约束非线性规划问题,引入Lagrange函数将其转化为无条件极值问题,有: (6) 其中,αi为Lagrange乘子。 对(6)式中的ω、b、ei、αi分别求偏导,可得(6)式的驻点,即令: i=1,2,…,N, 从而如下方程组成立: (7) 消去(7)式中的ω和ei,可以将(7)式化为如下的线性方程组: (8) 其中:1=[1 1 … 1]T;Ω=(Ωij)n×n,Ωij=φ(xi)Tφ(xj)=K(xi,xj);α=[α1α2…αn]T;Y=[y1y2…yn]T。 由(8)式可以得到模型参数b和α1,α2,…,αn的估计,从而LSSVR算法的预测模型为: (9) 鲸鱼优化算法(whale optimization algorithm,WOA)是由文献[16]于2016年提出的模仿座头鲸捕猎行为的一种新的仿生智能算法,具有操作简单,调整参数较少和跳出局部最优解的能力强等特点,可运用于模型参数优化等问题。 在WOA算法中,假设在一个D维的空间中,有n个鲸鱼组成了一个种群X={X1,X2,…,Xn},其中个体Xi=(xi1,xi2,…,xiD)是该鲸鱼在空间中的位置,它表示解空间中的一个解;解空间中的最优解可以抽象为猎物的位置。WOA算法分为3个部分,分别是环绕捕食、泡泡网攻击以及搜索捕食。 (1) 环绕捕食。座头鲸在捕食时,可以识别猎物的位置并对其进行包围,该行为可以由下式表示: Xi(t+1)=X*(t)-A·D (10) D=|C·X*(t)-Xi(t)| (11) 其中:“·”为矩阵的Hadamard积;| |为向量的每一个分量取绝对值后构成的新向量;X*(t)为迭代到第t次时当前种群最优解的位置;A=a(2r-1)、C=2r为系数向量,1=[1 1 … 1]T,r为[0,1]上的随机向量,a为在迭代的过程中从2到0线性下降的控制参数。 (2) 泡泡网攻击。在WOA算法中,运用收缩包围机制和螺旋更新位置机制模拟泡泡网攻击的行为。 收缩包围机制可以通过减少a的大小实现,当A的每个分量在[-1,1]时,鲸鱼会通过(10)式、(11)式在原始位置和当前最优位置之间选择任意的位置。 螺旋更新位置机制的实现是通过在鲸鱼和猎物之间建立螺旋方程,即 Xi(t+1)=D′eblcos(2πl)+X*(t) (12) D′=|X*(t)-Xi(t)| (13) 其中:b为控制螺旋形状的参数,通常取b=1;l为[-1,1]上的随机数;| |含义同上。 为了模拟泡泡网攻击行为,WOA算法认为这2种机制发生的概率相同,即各为50%。因此构建如下的算法模型: (14) (3) 搜索捕食。在实际的捕食过程中,个体会根据其他个体的位置随机搜索食物,在搜索捕食的机制下,个体通过随机选择其他个体的位置代替最优个体的位置,以增强算法在全局范围内的搜索能力。该机制的算法可以表示为: Xi(t+1)=Xrand(t)-A·D (15) D=|C·Xrand(t)-Xi(t)| (16) 搜索捕食机制是通过控制参数a的变化来控制的。当|A|<1时,选择最优个体位置更新,即(10)式、(11)式;当|A|≥1时,选择随机个体位置更新,即(15)式、(16)式。 在用LSSVR模型对数据进行预测时,预测精度很大程度上依赖于γ和σ的选取。其中:γ为惩罚系数;σ为核函数半径。γ越大,分类越严格,允许错分的样本受到的限制越大,错分的样本数少,容易出现过拟合,泛化能力差;γ越小,允许错分的样本受到的限制越少,容易出现欠拟合。σ越小,模型只作用于支持向量样本附近,训练效果好,但预测效果差;σ越大,越容易出现平滑效应,造成训练效果差。因此选取合适的γ和σ显得尤为重要。 本文结合WOA算法对LSSVR中的参数γ和σ进行优化,利用最优的参数对数据进行预测。同时为了防止过拟合导致训练效果好但预测效果差,本文运用留出法(hold-out)将数据X分为训练集S、验证集T和测试集P。在训练集S上训练模型,用验证集T评估模型的测试误差,作为对泛化误差的估计。为此,本文构建新的基于非结构化数据的LLE-WOA-LSSVR组合预测模型的流程如图1所示。 图1 基于非结构化数据的LLE-WOA-LSSVR组合预测模型 基于非结构化数据的LLE-WOA-LSSVR预测模型的步骤如下: (1) 收集相关的非结构化数据X={X1,X2,…,Xn}。 (2) 运用LLE降维方法对原始样本集X进行降维处理,得到低维样本集Y,并将样本集Y划分为训练集S、验证集T和测试集P。 (3) 利用WOA算法优化LSSVR模型参数γ和σ。 1、在高位推动上联合。切实把宣传定位于卫生计生工作的重要位置,纳入卫生计生目标管理责任,在日常工作中更加突出宣传先行先导的作用。 (4) 结合优化后的γ和σ,利用LSSVR模型对训练集S进行训练,适应度函数为验证集T的误差平方和。 (5) 利用训练后的模型对测试集P中的数据进行预测,并进行误差分析,比较多种预测方法之间的优劣。 为了评价基于非结构化数据的LLE-WOA-LSSVR预测模型的有效性,本文利用2015年1月1日至2018年6月30日的百度指数数据对碳价格进行预测。通过在百度指数中输入相应的关键词,可以得到每日用户对关键词的搜索量。本文选取碳汇、碳足迹、碳交易、碳关税、碳排放、低碳经济、减排、碳中和、低碳生活和低碳这10个关键词作为影响碳价格的因素。所有实验是在Windows 10,MATLAB R2017a环境下进行的。 运用LLE算法对10组数据进行降维处理,本文将数据降成二维数据h1、h2,选取参数为k=3,每个样本点距离最近的3个点作为近邻点。运用得到的h1、h2和前一期的碳价格作为训练集,运用LSSVR算法预测碳价格。 为了防止过拟合,本文采用留出法,选取2015年1月1日至2017年12月29日的数据作为训练集,2018年1月2日至2018年2月28日的数据作为验证集,2018年3月1日至2018年6月30日作为测试集。利用WOA算法优化参数γ和σ,以验证集的误差平方和为适应度函数;另外,WOA算法的相关参数中,令种群数量为30,最大迭代次数为500,γ的取值区间为[0.01, 6 000],σ取值区间为[0.01, 100],得到γ=6 000,σ=49.343 1为最优参数。运用最优组参数,使用LSSVR工具箱程序预测数据,得到预测结果。 为了说明本文方法的有效性,选取如下预测模型进行对比分析: (1) 采用非结构化数据加入WOA算法寻优的LLE-WOA-LSSVR组合预测模型,记为模型一,即本文算法。 (2) 采用结构化数据且加入WOA算法寻优的模型,记为模型二。 (3) 采用非结构化数据未加入WOA算法寻优的模型,记为模型三。 (4) 采用结构化数据且未加入WOA算法寻优的模型,记为模型四。 (5) 无LLE降维算法,采用非结构化数据加入WOA算法寻优的模型,记为模型五。 本文采用的结构化数据是碳价格的时滞为3期的数据,即利用前3期数据作为预测下一期的标准。先将前4种预测方法的结果进行比较,如图2、图3所示。 图2 4种预测方法训练和测试结果 从图2可以看出,4种预测方法的训练和测试结果,与实际值相比,趋势基本一致,拟合程度较好,没有太大的误差。为了对比4种预测方法的泛化能力,对预测集结果进行单独比较,结果如图3所示。 图3 4种预测方法预测集结果 从图3可以看出,4种方法和实际值相比,整体变化趋势一致,误差在可接受范围内,本文所用的方法与实际值更接近。此外,为了分析降维方法对预测模型是否有效,比较模型一和模型五,分析降维方法引入的合理性,结果如图4所示。 图4 有LLE降维和无降维模型预测结果和误差图 从图4可以看出,引入LLE降维方法后,结果与无降维方法,直接使用WOA+LSSVR预测模型的结果总体差距不大,从误差大小来看,本文提出模型总体误差较小。为了比较不同模型更加精确的预测能力,现引入5种误差度量标准进行误差分析。 为了比较不同预测模型之间的优劣性,体现非结构化数据和WOA算法优化参数对模型求解的优势,多种误差标准被用来评价模型的有效性。本文采用的误差度量标准是SSE、MSE、MAE、MAPE和MSPE,见表1所列。 表1 5种误差度量标准 将本文模型(模型一)得到的预测结果与其他4种方法得到的预测结果进行比较,得到测试集的误差结果见表2所列。 表2 4种预测方法参数和测试集误差结果比较 从表2可以看出,本文所提出的组合预测模型一在5种误差标准下的值均为最小,这表明本文所用的方法是4种预测方法中最优的。 另外,对比模型一和模型三,可以发现运用了WOA算法寻优后,效果比直接运用LSSVR模型预测的精度要高,说明将智能算法和仿生寻优算法结合的可行性与有效性。对比模型二和模型四也有类似的结论。对比模型一和模型二,可以发现在考虑非结构化数据后,效果相较于只考虑结构化数据得到的结果要优,这表明非结构化数据在数据预测方面提供更多的信息。对比模型三和模型四,也有类似的结论。 同时,将无LLE降维的模型和其他4个模型对比可以发现,本文提出的模型一在各项误差上都有显著提高,并且模型二至模型四的误差也略优于无LLE降维的模型,这说明运用了LLE降维算法后,预测的精度有明显提高,表明降维并没有导致主要信息的缺失,同时降维后数据量的减少会提高模型计算的效率,说明降维算法在实际问题中的合理性。 综上所述,本文提出的基于非结构化数据的LLE-WOA-LSSVR碳价格组合预测模型具有较好的可行性和适用性。 为了解决碳价格的预测问题,本文首先引入非结构化数据,完善数据的信息完整性;其次利用LLE降维算法,将搜集到的10个影响碳价格的非结构化数据降成二维数据,并与滞后一期的碳价格构成影响碳价格的因素,运用LSSVR模型对训练集数据进行训练,并将测试集数据的误差作为适应度函数,结合WOA优化算法对参数优化,得到预测结果;最后比较4种不同预测方法的预测结果并分析误差,发现本文提出的基于非结构化数据的LLE-WOA-LSSVR碳价格组合预测模型的精度最高,说明本文模型具有较高的可行性和有效性。在未来的研究中,可以对WOA方法中的参数,以及种群初始化进行优化调整,使算法收敛速度更快,提高运算精度和运算时间。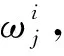
1.3 LSSVR
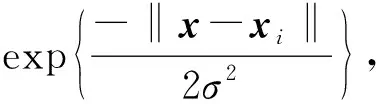
1.4 WOA优化算法
2 LLE-WOA-LSSVR组合预测模型构建
3 案例分析

4 5种预测模型的误差分析

5 结 论
