大跨度桥梁颤振时域的直接分析法

张鸣祥, 廖海飞, 王建国, 周晨曦

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.土木工程防灾减灾安徽省工程技术研究中心,安徽 合肥 230009)

通常的桥梁风振分析多借助于频域内的分析方法,因而多局限于线性范围。近年来超大跨度桥梁不断兴建,有必要在风振响应分析中计入结构及荷载的非线性影响,故有必要讨论风致振动的时域分析。文献[1-3]提出用单位脉冲响应函数描述自激力,文献[4-5]将其在三维空间内扩展;文献[6]建立基于自激力脉冲响应函数的桥梁颤振运动方程并给出2种时域求解方案;文献[7-8]发现静风作用引起的结构动力特性对大跨度桥梁颤振稳定性的影响显著,必须在颤振分析予以准确考虑;文献[9]结合断面的颤振导数,采用文献[10-11]提出的阶跃函数对桥梁断面自激力进行模拟,并对模拟准确性进行分析与校核,推导出时域颤振动力有限元分析中自激力的递推表达式;文献[12]运用状态空间法对大桥进行三维颤振分析;文献[13]提出统一的颤振和抖振时程分析方法,并考虑结构的几何非线性和气动非线性,该方法以非线性有限元的直接积分法为基础,在研究中具体解决了随机风速场的模拟、耦合自激力的时域计算和统一的颤抖振时程分析流程等关键问题。

本文采用三维空间内的单位脉冲响应函数描述自激力的方法,改进传递函数最小二乘法的拟合方法,从自激力时域描述公式中分离出气动质量,使得公式中的时间历程与当前时间无关,以期消除迭代计算中由自激力时域公式引起的荷载非线性,提高计算速度和计算精度。

1 基本理论

结构在均匀流作用下的颤振响应动力微分方程组为：

(1)

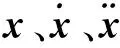
1.1 自激力的脉冲函数

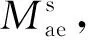
(2)

其中:Frs(r=D,L,M;s=h,p,α)为各自对应的脉冲响应函数,h、p、α为主梁竖向、横向及扭转位移关于时间t的函数;B为桥面宽度。以FM α(t)为例,其表达式为:

(3)

其中:ρ为空气密度;u为风速;C1,C2,…,Cn,d3,d4,…,dn为待定系数,且满足

(4)

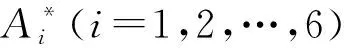
(5)

Rk=dku/B,

观察(5)式发现,其中含有ti+1项,即当前时刻项,并不是单纯地与ti+1之前的时间历程有关,若直接用于计算,则须进行迭代[14]。为此,设

(6)

(7)

将(5)式代入(6)式可得:

(8)

再将(7)式代入(8)式可得:

(9)

如此,可得到新的递推公式,即(3)式可以写成:

(10)

kM α=ρu2C1,

(11)

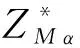
1.2 待定系数的求解

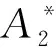
(12)

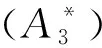
使用同样的方法依次求得FL h、FL p、FL α、FD h、FD p、FD α、FM h及FM p的待定系数和表达式。由于目前试验条件和方法的限制,对于不能获得的颤振导数一般设为0。

2 有限元程序设计

当使用有限元软件分析时域内的颤抖振时,每个单元上所作用的气动力和抖振力均可以分离出气动刚度、阻尼、质量及节点荷载向量。

对于空间梁单元所受的气动力,按(2)式可以分离出气动刚度、阻尼和质量,若按照类似于集中质量矩阵处理方法,分别可以表示为:

(13)

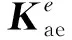
(14)

(15)

(16)

对于剩下的时间历程项,则可以作为节点荷载来处理,即

(17)

(18)

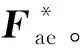
根据上述分析可以得到结构在均匀流作用下的颤振响应动力微分方程组为:

(19)

可采用ANSYS的Matrix27单元输入自激力的气动刚度矩阵、气动阻尼矩阵和气动质量矩阵,在每个要求计算自激力的节点施加3个Matrix27单元,每个单元的一个节点为施加自激力的结构节点,另一个节点全约束。ANSYS中自激力分析示意图如图1所示,单元e的节点i处用于模拟气动刚度、气动阻尼及气动质量的单元分别为e1、e2、e3,e1、e2、e3共用节点i、j。此时单元e分配到节点i、j的气动刚度矩阵、气动阻尼矩阵和气动质量矩阵作用于各Matrix27单元的气动刚度矩阵、气动阻尼矩阵和气动质量矩阵可以分别为:

(20)

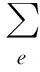
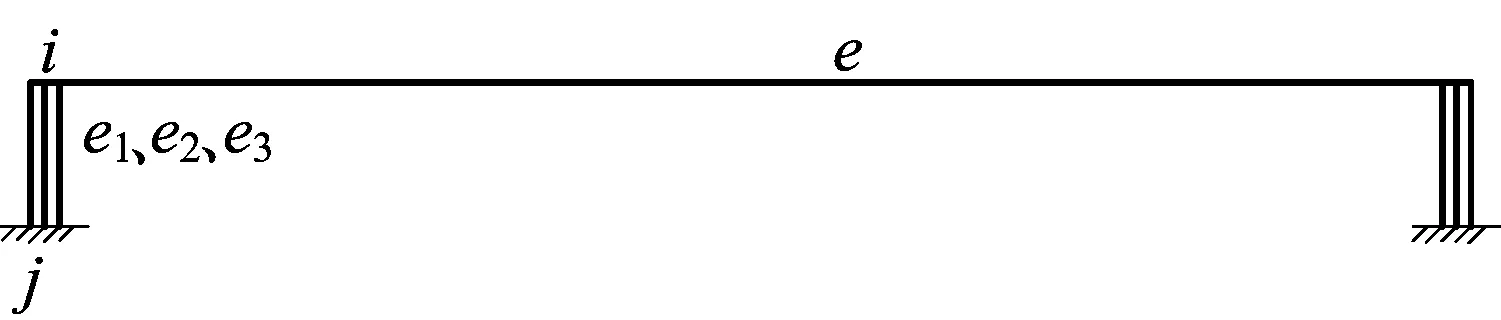
图1 ANSYS中自激力分析示意图

因此,根据上述分析,利用ANSYS中提供的APDL语言和应用MATLAB编制的自激力传递函数拟合程序在ANSYS中能够实现颤振时域时程分析程序。

3 算 例

3.1 具有理想平板截面的简支梁

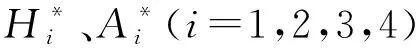
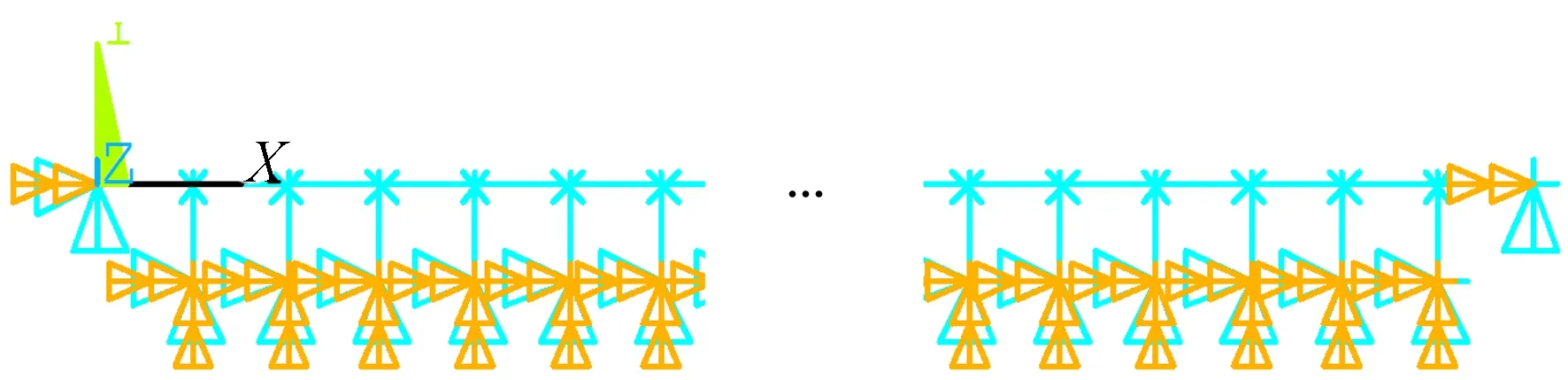
图2 理想平板简支梁的颤振时域分析有限元模型

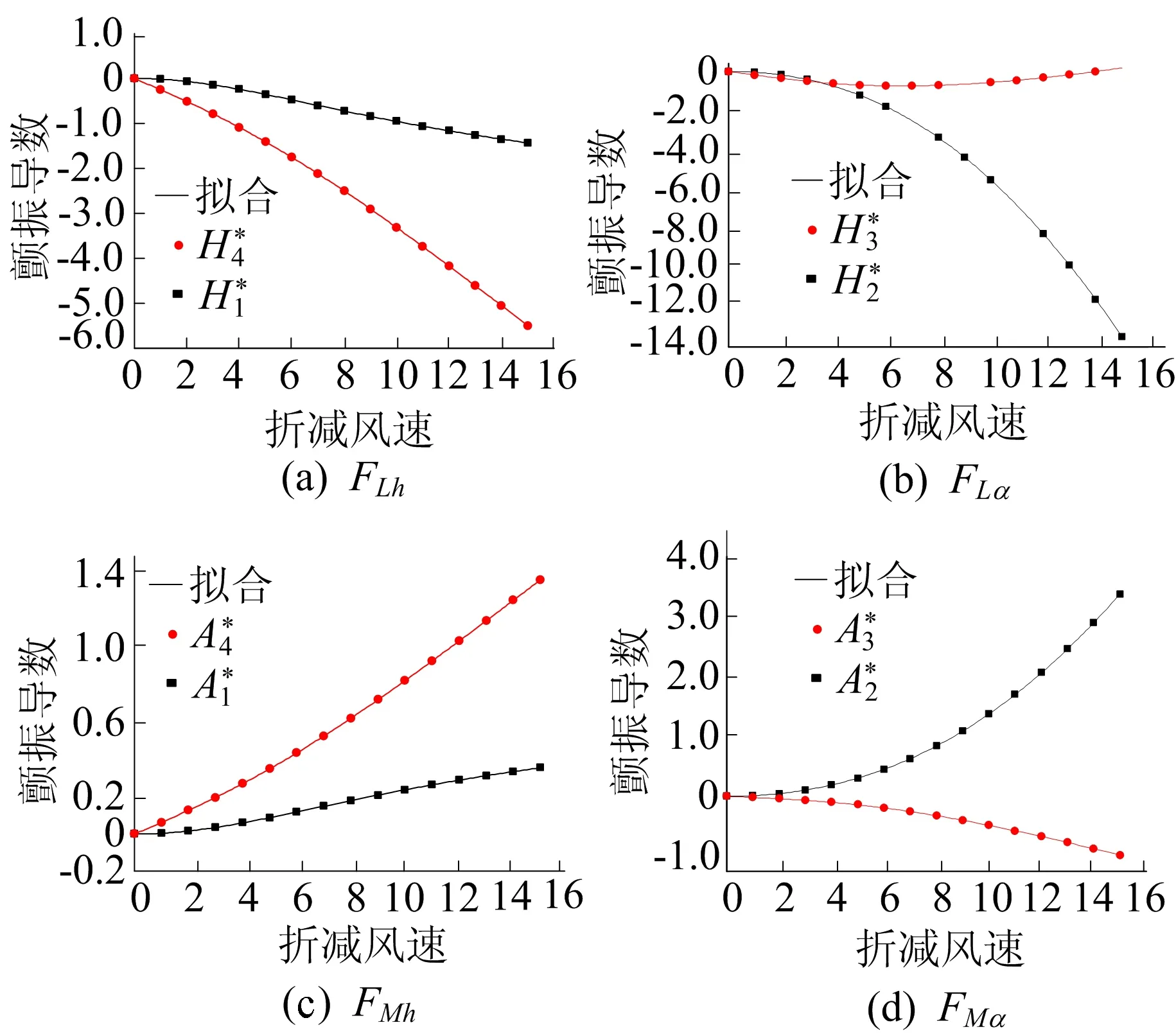
图3 理想平板简支梁拟合、实际颤振导数曲线对比

0°风攻角时,风速分别为135.00、137.50、140.00 m/s作用下简支梁颤振响应如图4所示。

图4d～图4f为竖向位移时程的快速傅里叶变换(fast Fourier transform,FFT)分析结果。理想平板简支梁颤振时域、频域分析的误差见表1所列。从图4、表1可以看出，结构在风速为137.50 m/s的均匀风作用下,处于颤振临界状态,频率为0.391 4 Hz,与频域分析结果较为接近,验证了本文分析方法在颤振临界风速和颤振频率上均具有足够的精度和可靠性,并具有非线性计算的能力。

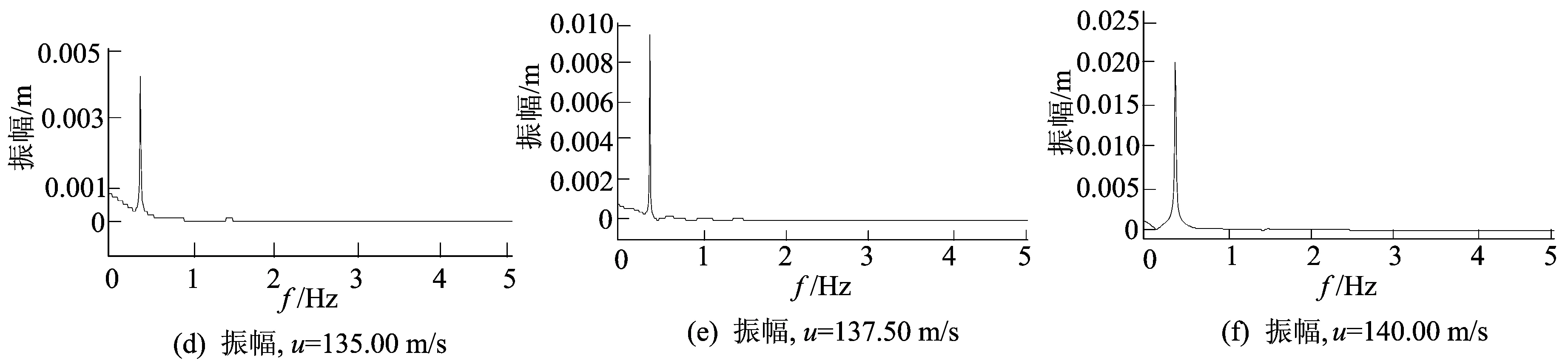
图4 均匀风3种风速作用下理想平板简支梁的颤振响应

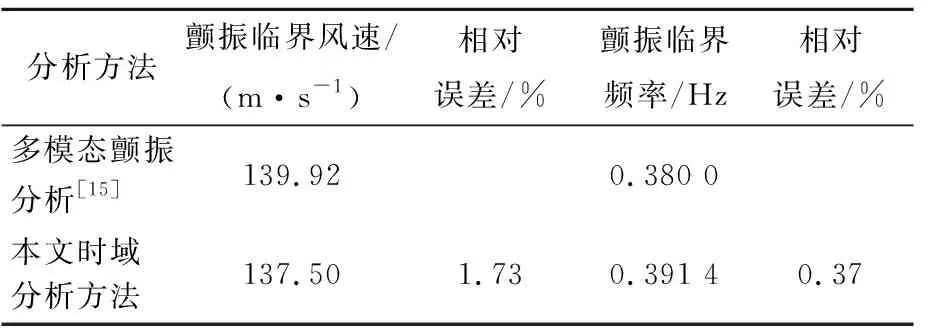
表1 理想平板梁颤振时域、频域分析误差

3.2 马鞍山长江大桥右汊桥

马鞍山长江大桥右汊桥(简称该桥为“大桥”)为主跨2×1 080 m三塔悬索桥,跨径布置为360 m+1 080 m+1 080 m+360 m=2 880 m,加劲梁采用闭口扁平钢箱梁,加劲梁高3.5 m宽38.5 m,加劲梁设上、下斜腹板构成导风嘴。索塔总高178.3 m,2条主缆横向间距为35.8 m。桥塔主体混凝土浇铸,成H型桥塔,中塔采用扩大三角支撑。大跨度三塔悬索桥与两塔单跨悬索桥相比,结构更为复杂,其中塔塔梁固结,全桥的振动响应与两塔单跨悬索桥有很大区别。建模采用单主梁模型,如图5所示,主要构件截面特性部分参数见表2所列,加劲梁泊松比为0.3,横向惯性矩为207.04 m4,竖向惯性矩为3.22 m4,质量惯性矩为2.59×106kg·m。

图5 马鞍山长江大桥右汊桥全桥有限元模型

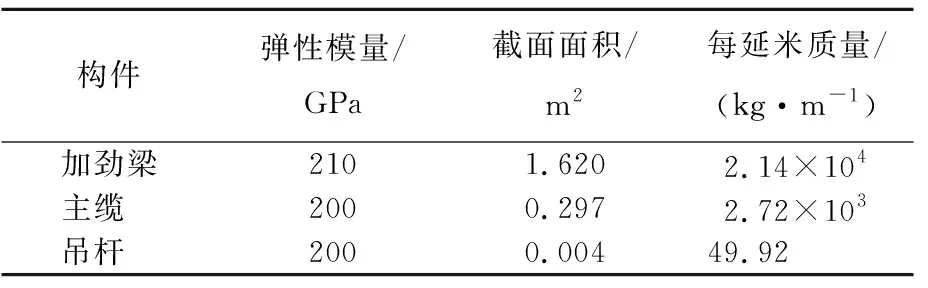
表2 大桥主要构件截面特性部分参数

大桥断面气动力传递函数系数拟合结果如图6所示。

图6中,离散数据为主梁节段风洞试验取得的颤振导数试验值。

根据桥梁场地情况,离地高度约为z=57.8 m,地面粗糙长度z0取0.01 m,假定所有的模态阻尼比为0.005。添加402个Matrix27单元模拟大桥自激气动力,其中134个Matrix27单元模拟气动刚度,134个Matrix27单元模拟修正气动阻尼,134个Matrix27单元模拟修正气动质量。

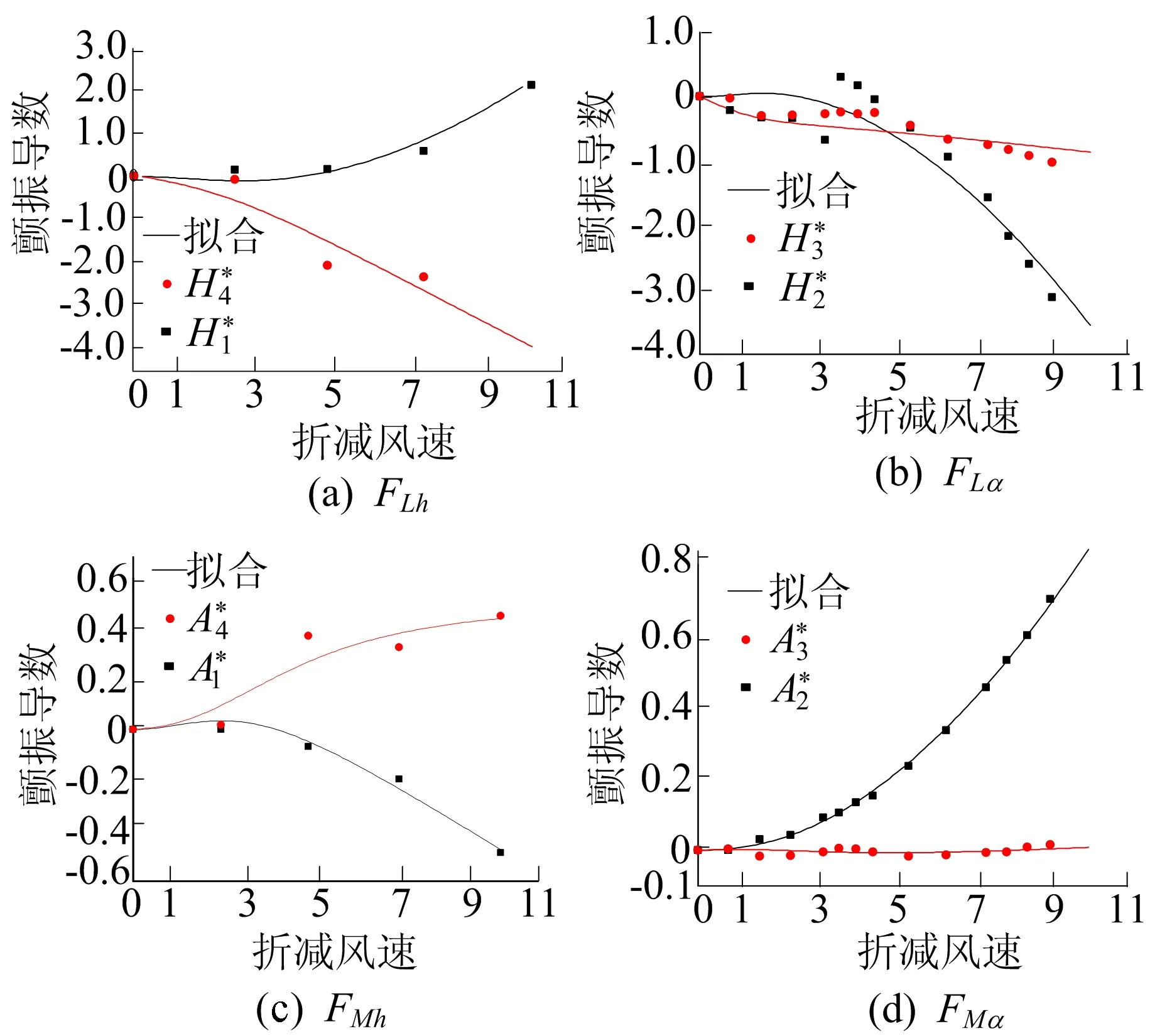
图6 大桥断面气动传递函数系数拟合结果

0°风攻角下,风速分别为60.0、64.0、69.0 m/s作用下大桥的颤振响应如图7所示。图7b、图7d、图7f为位移时程的FFT分析结果。大桥时域、频域的分析误差见表3所列。从图7、表3可以看出，结构在风速为64.0 m/s的均匀风作用下,处于颤振临界状态,频率为0.207 4 Hz,同频域分析结果较为接近。

由于该桥的颤振导数数量相对较少且连续性较差,与具有理想平板截面的简支梁的结果相比,该桥时域、频域颤振分析结果的相对误差较大,可见颤振导数连贯性对颤振临界风速和颤振频率的分析影响较大。

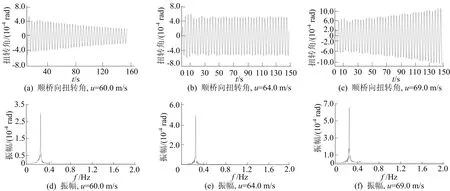
图7 均匀风3种风速作用下大桥的颤振扭转响应

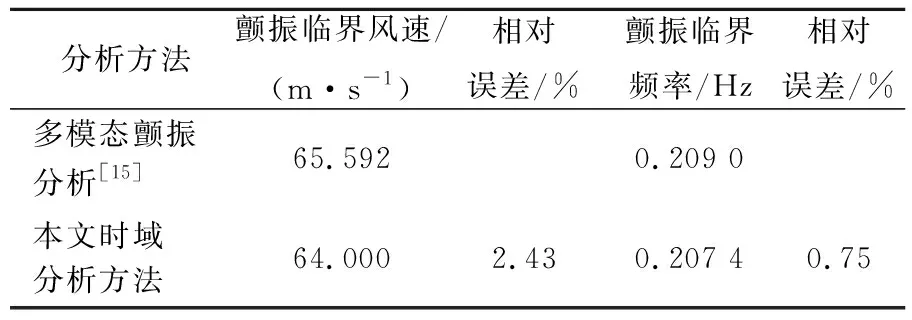
表3 大桥的时域、频域颤振分析误差

4 结 论

(1) 本文采用三维空间内单位脉冲响应函数描述自激力的方法,改进传递函数最小二乘法的拟合方法,并从自激力时域描述公式中分离出气动质量,使得公式中的时间历程与当前时间无关,消除了迭代计算中由自激力时域公式引起的荷载非线性,提高了计算速度和计算精度。

(2) 对具有理想平板截面的简支梁颤振时域分析结果表明，本文分析方法在颤振临界风速和颤振频率上均具有足够的精度和可靠性,并具有非线性计算的能力。

(3) 以马鞍山长江大桥右汊桥(三塔两跨悬索桥)为例,进行颤振的时域数值计算,结果表明时域、频域计算结果较为接近,但是相对误差较具有理想平板截面的简支梁有所扩大。实际工程中颤振导数连贯对传递系数的拟合有重要的影响,颤振导数连贯性对时域内颤振临界风速和颤振频率的分析影响较大。