“四个理解”视角下的椭圆及其标准方程的教学研究

安徽省宿州学院附属实验中学 马 杰 （邮编：234000）

安徽省宿州市第三中学 王 辉 （邮编：234000）

2017 年4 月，在“以核心素养为纲的数学教学改革”的研讨会上，章建跃博士完善了他提出的“四个理解”，即理解数学、理解学生、理解教学、理解技术.这为广大一线教师的教学提供了风向标，是数学教学活动的基础，也是教学的一个重要抓手.2021 年11 月4 日，笔者在宿州三中的录播室中聆听了王辉老师的一节示范课，课题名称是“椭圆及其标准方程”，教学设计理念来自于对“四个理解”的认识，教学思路清晰，教学手段丰富，以小组合作探究的方式完成了本节内容的教学，培养了学生的数学抽象、直观想象、逻辑推理、数学运算等核心素养.现把王老师的教学思路和笔者的一些教学思考，整理成文，以飨读者.

1 从概念本质特征上——理解数学

美国认知教育心理学家奥苏贝尔曾说：“在向学生传授新知识之前，给学生一个短暂的具有概括性和引导性的说明.”本节是北师大版选择性必修第一册第二章“圆锥曲线”的起始课，在教材的章节导入语中，明确了“圆锥曲线”的概念，即用平面去截圆锥面，根据截面与圆锥面的轴的夹角不同，所得的截线分别是圆、椭圆、抛物线、双曲线，并把它们统称圆锥曲线.它揭示了该章名称的由来，作为学生对圆锥曲线认知的起点，能有效激发学生对本章的整体认知结构，建立与前面已学的知识联系，引导学生我们接下来需要研究的主题，因此，本节课的教学无论从数学思想上，还是数学方法上对全章起到引领作用，有效地发挥了章节导入语的价值.

理解数学重在抓住数学的本质，椭圆的本质特征就是椭圆上的任意一点到平面两定点的距离之和为常数（该常数大于两定点之间的距离），这也是1579 年意大利画家蒙蒂对椭圆的定义.教学中充分利用几何画板、细绳画椭圆以及丹德林双球模型的微视频，目的是让学生用数学的眼光去观察动点在运动变化中的规律，寻找运动变化中的不变性，有利于学生抓住这一根本，明晰椭圆的概念，理解数学知识，从而为探究椭圆的方程和性质奠定坚实的基础，也为本单元的知识学习整体构建框架，符合新课程倡导的单元教学理念.

2 从学生思维规律上——理解学生

在此之前，学生在上一章已经学习了直线和圆，已经初步经历和体验了研究解析几何的方法——坐标法，所以，学生对用坐标法研究本节内容，并不陌生，已有相关知识经验，为顺利开展本节课的教学提供了方法保障.由于本节课的教学重点就是椭圆的定义和标准方程的推导，同时这也是本节的难点.教学中，让学生根据动画演示、微视频、细绳画椭圆，都是为了激发学生的数学思维，经过教师的引导，类比圆的定义，抽象出椭圆的定义.在得到椭圆的标准方程之前，教师设计了一系列的问题，提醒学生遵循对称的观点建立合适的坐标系，利用推导圆的标准方程的方法，得出方程2a，对方程的化简到(a2-c2)x2+a2y2=a2(a2-c2)后，引导学生类比圆的标准方程的简洁、优美的形式，小组讨论，得到椭圆的标准方程，这个运算过程需要学生有沉着冷静的思维品质，特别有利于提升数学运算这一核心素养.因此，理解学生就是要遵循建构主义的观点，既不能把问题设计的太难，也不能把问题设计的没有思维含量，要以“不捅破窗户纸为最佳”.这样才能做到，通过教师的教学帮助学生逐步学会更清晰、更深入、更全面的、更合理地进行思考，并能由“理性思维”逐步走向“理性精神[1]”.

3 从把握教学规律上——理解教学

课堂是教师教学的主阵地，是学生学习知识的加油站.充分把握教育规律，遵循学生的认知心理，循序渐进，逐步让学生自主构建知识.学生的学习就是在澄清问题、分析问题、解决问题的过程中得以不断推进的[2].因此，课堂教学中，王老师采用以问题为导向，注重对学生思维的引导，加强学生的理解力的培养，从而给学生提供一个知识架构.主要教学过程,摘录如下:

3.1 认识椭圆

问题设计请大家观察幻灯片中常见的图片，如图1、图2，回答问题：

图1

图2

你看到了什么形状？你还有哪些生活经验能生成椭圆？

设计意图从行星运动轨迹到生活中的椭圆，学生在感叹大自然的神奇的同时，激发学生的学习兴趣.

3.2 形成概念

在教学中，如何点拨才能让学生发现椭圆的本质特征.王老师采取了三个措施：利用微视频播放丹德林双球模型、利用几何画板动态演示、学生合作用细绳画出椭圆，三个活动都具有明确的指向性——凸显椭圆的本质，进而构建概念.

图3

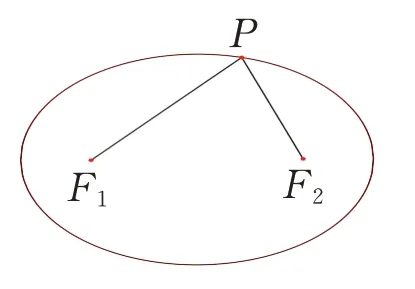
图4

问题设计观看丹德林双球模型的微视频你发现了什么？根据几何画板的动态演示，观察动点的运动过程，有什么样的发现？利用细绳画出的椭圆的过程中，什么是一直不变的？当绳长等于两定点距离以及小于两定点之间的距离的时候，能画出动点的轨迹吗？

追问你能类比圆的定义得到椭圆的定义吗？

设计意图心理学家皮亚杰指出:“活动是认识的基础，智慧从动手开始.”学生在实验操作中，体会椭圆的定义特征；在小组活动中，培养学生的合作、探究意识，通过设置的问题的引导，自然生成了椭圆的概念.

3.3 推导方程

问题设计推导直线和圆的方程的方法是什么？能利用这种方法去推导椭圆的方程吗？

请小组讨论如下建系方案：

方案1以定点F1为原点，两定点的连线为x轴；

方案2以定点F2为原点，两定点的连线为x轴；

方案3以定点F1、F2的连线为x轴，它的垂直平分线为y轴；

方案4以定点F1、F2的连线为y轴，它的垂直平分线为x轴；

根据你建立的坐标系，你能写出动点满足的集合吗？

追问1类比圆的标准方程如何化简这个方程吗？（小组合作，利用平板电脑上传化简结果，教师进行分析）

追问2当椭圆的焦点在y轴上时,它的标准方程是怎样的呢?

设计意图让学生在实际操作中，体会到数学的对称之美、简洁之美.建立平面直角坐标系，得到点P满足的集合{ }P||PF1|+|PF2|=2a，利用两点间的距离公式容易得到方程，引导学生从不同的思路去化简.当椭圆的焦点在y轴上时,学生经过观察、思考会发现，只要交换坐标轴就可以了，从而得到了焦点在y轴上的椭圆的标准方程.

这种小组的合作讨论，学生体验了不同思路的思维碰撞（有的平方化简，有的分子有理化等），体会求曲线方程的一般方法即建系、设点、列式、化简、检验，形成了学习椭圆知识过程中基本活动经验，为抛物线、双曲线的后续学习提供建构基础.

3.4 知识深化

问题设计请同学们完成以下表格

x2 y2 y2 x2标准方程b2=1(a ＞b ＞0)a2 +b2=1(a ＞b ＞0)____a2 +不同_______点相同__________点图形形状焦点坐标______________________________________椭圆________________________________________定义a、b、c 三者关系_____________________________________

设计意图让学生对椭圆知识结构有一个整体的认知，把知识系统化、网络化，培养学生直观想象、数学抽象等素养，让学生体验数形结合、分类讨论等数学思想.

3.5 巩固应用

例1（1）在平面内，若动点P到A(-3,0)，B(3,0)的距离之和为8，则点P的轨迹是______;

（2）在平面内，若动点P到A(-4,0)，B(4,0)的距离之和为8，则点P的轨迹是______;

（3）在平面内，若动点P到A(-1,0)，B(1,0)的距离之和为1，则点P的轨迹是______.

例2已知椭圆的两个焦点F1、F2坐标分别为(-2,0)，(2,0)，点，求椭圆的标准方程和三角形PF1F2的周长.

设计意图通过例题的学习，重点考察椭圆的基础知识，让学生理解的基础上掌握椭圆的概念和求椭圆标准方程的基本方法.

3.6 课堂练习

（2）求适合下列条件的椭圆标准方程：

①a=，b=1，焦点在x轴上；

②焦点为（0，-3）,(0,3)且a=5.

（3）（思考题）已知点C(2,0)为圆A：（x+2）2+y2=36 半径上一点，点M在圆A上，作MC的中垂线交AM于点P，当点M在圆A上运动时，求点P的运动轨迹.

设计意图课堂练习分层，起到了巩固椭圆知识的作用，思考题是本节课数学思想与方法的延续，起到单元教学的一体性的作用.

4 从服务数学教学上——理解技术

《普通高中数学课程标准（2017 年版2020 修订）》（以下简称《标准》）在教学建议中要求，“重视信息技术运用，实现课堂技术与数学课程的深度融合[3]”.为了把本节教学与信息技术充分融合，选择的教学场所是一间多功能教室，兼有智慧课堂和录播室的功能.因此，无论是教师的教学展开还是学生对问题的解决，都可以平板电脑上进行，这也为学生的深度学习提供一个环境和氛围.节约了和认知体验.例如，先利用微视频播放丹德林双球模型，再到运用几何画板制作的动画展示等内容，直观地展示了椭圆形象，这既节约了时间又增加了课堂教学容量；在课堂练习环节，老师先设置好答案，充分利用平板电脑的统计和投屏功能，及时总结学生的错误地方，特别对那道思考题的教学，部分学生利用几何画板自主探究了动点的轨迹问题.这些认知体验，是无法由他人替代的，印象是深刻的，促进了对学生椭圆概念的理解，对凸显教学重点、突破教学难点提供帮助，有利于培养学生的直观想象、逻辑推理等素养，为教学的顺利开展提供了积极的辅助作用.

5 教学思考与启示

《标准》指出：通过高中数学课程的学习，学生能获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验（简称“四基”）[3].本节课在“四个理解”的基础上，以问题为引领，以信息技术为辅助，围绕“平面内与两个定点F1、F2的距离之和等于常数（常数大于|F1F2|）”来设计教学，落实教学的基本知识；运用所学的知识解决椭圆的问题，促进了学生基本技能的发展；利用平面直角坐标系推导出椭圆的标准方程，体现了数形结合的基本思想；学生经历了由形入数，再由数入形的过程，在这个过程中，让学生获得关于椭圆知识的这一基本活动经验.因此，“四个理解”是指导教师进行课堂教学的定海神针，能培养学生的“四基”，发展学生的数学核心素养，当然“四个理解”是一体的，互为表里，不能割裂，才能落实新课程下的单元教学理念.