基于特征系数灵敏度的鲁棒极点配置＊

蒋小平,陈晓飞

(中国矿业大学(北京)机电与信息工程学院，北京 100083)

1 引言

鲁棒性原是统计学中的一个专门术语，20 世纪70年代初开始在控制理论的研究中流行起来，用以表征控制系统对特性或参数摄动的不敏感性[1]。由于鲁棒性这一性质，随着在工程中对控制系统的精度以及稳定性的要求逐渐严格，鲁棒控制便早已成为控制届的重要问题，在控制理论课程中的地位也是愈来愈重要。极点配置作为改善线性时不变系统性能指标的常用技术方法之一，其鲁棒极点配置的相关问题研究相应有着很重要的教学和研究意义。关于鲁棒极点配置问题的研究，为了方便鲁棒系统设计，要引入了一些鲁棒指标，进而提出了各种最优鲁棒极点配置方法。但遗憾的是，大多指标较难计算，且最优鲁棒极点配置方法具有一定的局限性。考虑特征系数灵敏度计算简单，本文把加权后的特征系数灵敏度作为鲁棒指标，目标函数的极小化采用标准的具有二次收敛性质的参数最优化方法。并且本着控制课程教学的目的，对原理进行详细讲解，设计实例验证算法的可行性。

2 线性系统

线性系统通常因某些不确定因素而无法精确建立，这就导致了系统的不确定性[2]。

具有不确定参数的线性时不变多变量系统可用下列状态方程描述[3-5]：

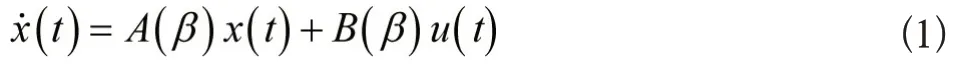
式中，x(t)∈Rn为状态向量；u(t)∈Rm为输入向量；β∈D∈Rr为不确定性参数向量(D 为β 的取值区域)，其名义值为β0；A(β)∈Rn×n，B(β)∈Rn×m是依赖于不确定性参数向量β 的系统矩阵和控制矩阵。

系统的特征多项式为：

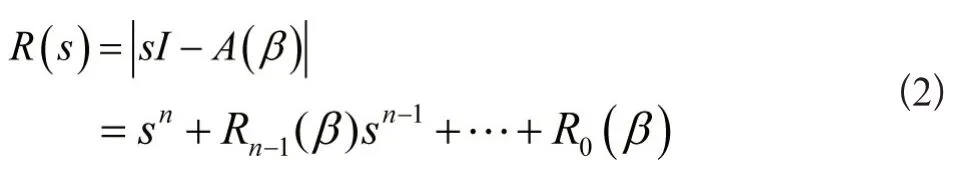
特征系数灵敏度定义为[6]：

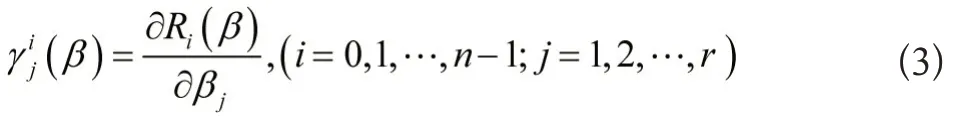
3 鲁棒极点配置

对于(1)式的线性时不变多变量系统，设计一个定常状态反馈控制器即可使系统具有期望的极点，从而满足系统的性能指标。

构成控制：

此时闭环系统变为：

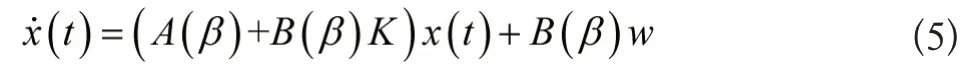
式中，K∈Rm×n为状态反馈增益矩阵；w∈Rm为外输入向量。

当不确定参数向量处于其名义值，即β=β0时，加了定常状态反馈器的系统极点精确的位于期望极点。当参数β 偏离名义值时，应保证系统的极点尽可能小的偏离期望极点，这就是鲁棒极点配置。一般的方法是极小化闭环极点对不确定参数向量β 的灵敏度来实现。根据文献[7-8]可知，极小化特征系数对不确定参数向量β 变化的灵敏度也可以有效实现鲁棒极点配置[5]。

β=β0时，假设[A(β0)，B(β0)，]能控，则根据极点配置原理知识可知，必定存在状态反馈矩阵为K 的定常状态反馈器，使该闭环系统具有期望极点。同时，若B(β0)的秩大于1时，参数在名义值状态下，可使闭环系统具有期望极点的状态反馈矩阵K具有无穷多个，这些K值共同构成一个集合。此集合中的每个K值对应的系统都有着不同的特征系数灵敏度，故只需取由特征系数灵敏度组成的某一式子作为性能指标，集合中的K值作为自变量，变化K值，使这一性能指标取得最小，就能很好的实现系统的极点鲁棒性。

假设闭环系统的期望极点均为单极点，取由特征系数灵敏度组成的性能指标

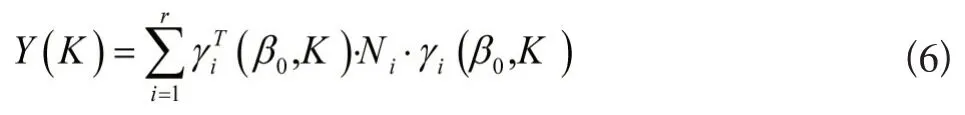
关于加权矩阵Ni的选取如式(7)所示：

式中，θi为与不确定参数βi变化范围的宽度成正比的正数，为期望极点对特征系数变化的灵敏度矩阵，如式(8)所示，其上标H表示共轭转置[9]。

不难证明：

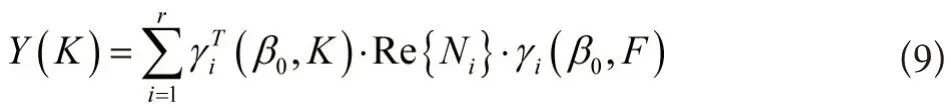
Re{Ni}表示取实部。

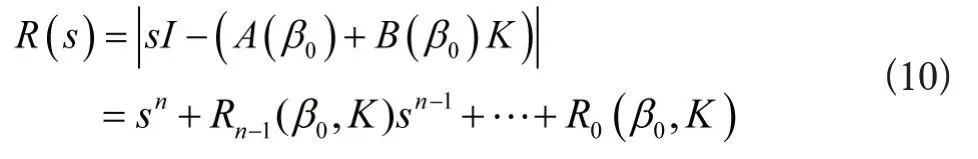
故此鲁棒极点配置问题转化成了有约束的最优化问题，如式(11)。

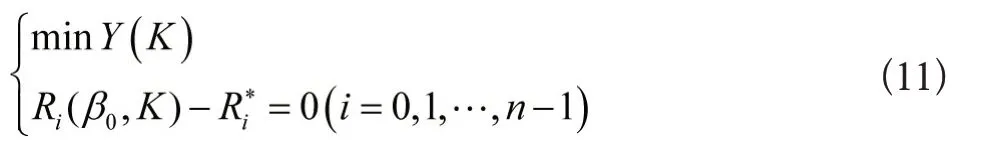
对此最优化问题，可采用外部罚函数将其转化为无约束最优化问题，转化后如式(12)。

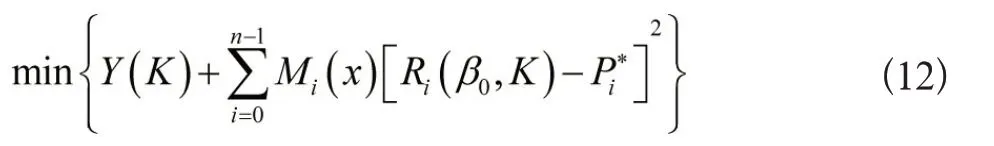
外部罚函数的具体步骤如下：

(1)初始化，给出K0初始值，惩罚因子Mi(1)的值和终止界限ε的值，令x=1。

(2)Yx-1为初始值，采用DFP算法求式(12)的极小值点Yx。

4 设计实例

假设具有参数不确定性线性系统的系统矩阵和控制矩阵分别为

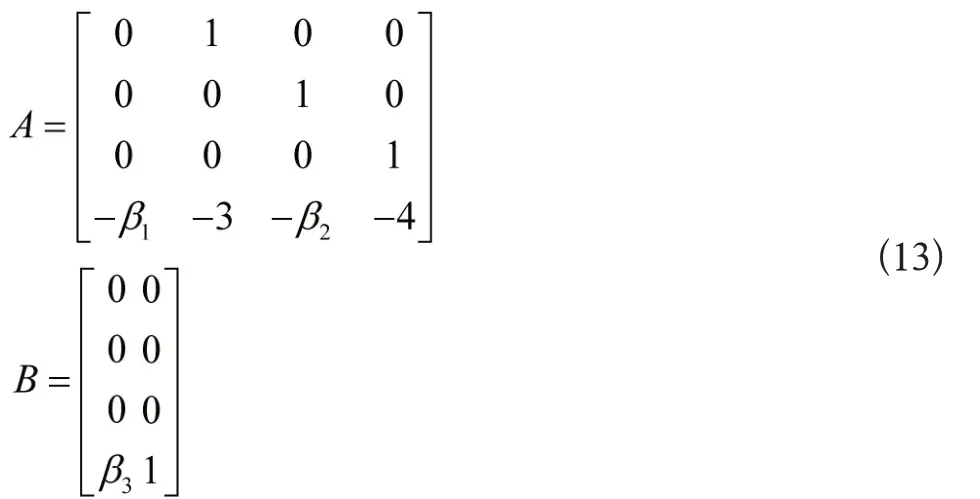
其中β1∈[0.8，1.2]，β2∈[1.9，2.1]，β3∈[0.7，1.3]。各不确定参数名义值为β1=1，β2=2，β3=1。闭环系统的期望极点分别为-1，-2，-1±j。

设状态反馈增益矩阵如式(14)，加了状态反馈控制器后的系统的特征方程式如式(15)

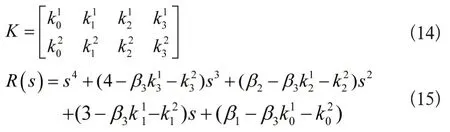
根据期望的闭环极点求出对应的特征方程如式(16)

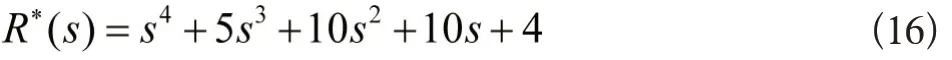
通过对特征系数灵敏的计算，求出其目标函数为式(17)

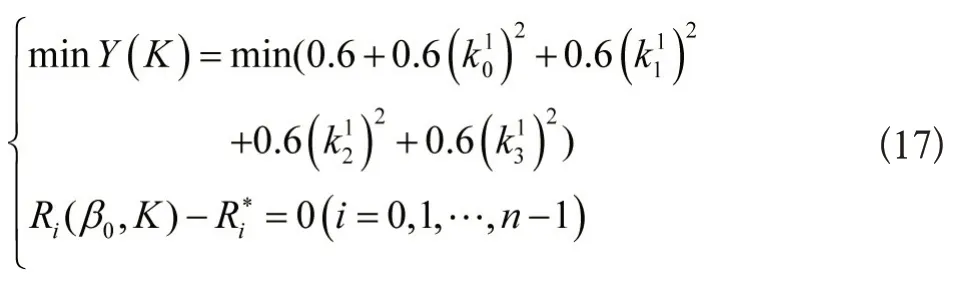
利用外部罚函数对此目标函数求解[10]，可得到极小值点为Yx=0.8895，此时的状态反馈增益矩阵为：

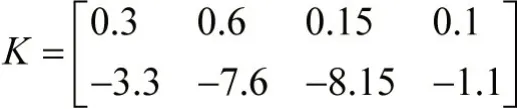
未进行极点配置的系统零极点图如图1所示，经过鲁棒极点配置后的系统的零极点图如图2所示，由图可知，闭环系统极点可以很好的置于期望极点处。

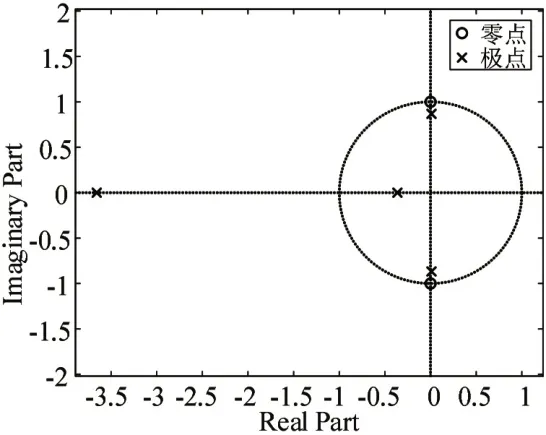
图1 原系统零极点分布图

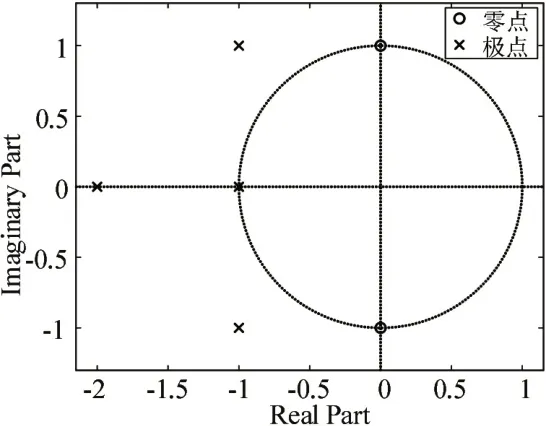
图2 鲁棒极点配置后系统零极点分布图

若将不确定变量中变化范围最大的β3由其名义值1 变为1.3，则此时系统的闭环零极点分布图如图3所示，图中可以看出系统的闭环极点并没有较大的偏离期望位置，故此时系统的极点具有相对较好的鲁棒性。

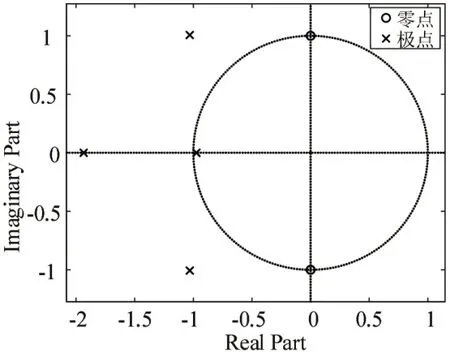
图3 β3为1.3时系统零极点分布图

5 结束语

本文利用加权的特征系数灵敏度作为鲁棒指标，介绍了一种鲁棒极点配置的方法，通过实例计算结果表明，高阶系统通过此算法可以得到理想的鲁棒极点配置效果，这也是该方法的显著优点。介绍该方法并且设计实验，对加深学生对相应的现代控制原理课程的重点内容的理解有着良好的促进作用，同时，理论联系实际，在提高学生学习和探究兴趣等方面也有着较好的促进作用。此方法中关于特征系数灵敏度组成的性能指标和式(7)所表示的加权矩阵还可进一步完善，实现系统更好的鲁棒性，这也为同学们留下了思考空间。