改进TOPSIS-RSR法在数控机床质量评价的应用

杨寒石,郑凯文,谭纪尧

（黑龙江大学电子工程学院，黑龙江哈尔滨 150080）

1 引言

数控机床是工业生产中金属零件加工环节的“机器母机”，是集成电、机、控制等多领域的复杂系统。在工业生产过程中，一旦数控机床出现质量问题导致停机生产中断，会严重影响企业效益。因而，在购置机床之前综合评价数控机床的质量显得至关重要。

评价的关键步骤是如何合理的计算指标的权重和选择评价方法。邱玉婷等人运用了熵权法计算了电能质量各项指标的客观权重，提出了相对贴近距离的概念，对传统TOPSIS 综合评价模型中存在某些情况下无法比较评价目标优劣的问题进行了改进，结合秩和比法，提出了基于改进的TOPSIS-RSR 的电能质量评价模型[1]。刘玉梅等人应用AHP 法计算可靠性每个等级的评价权重，并在物元模型中引入疲劳累积损伤理论和雨流计数法，提出了高速轨道车辆传动系统可靠性评价的物元模型[2]。胡国强等人应用AHP法和熵权法分别确定主、客观权重，并根据最小相对信息熵理论和拉格朗日乘数法计算得到组合权重，提出了高等学校讲师教学质量评价模型[3]。邱玉婷等人采取熵权法计算评价指标的权重，尽管能够体现指标的信息量，但没有参考评价指标的实际情况，使得所求权重可能会与实际情况不符。刘玉梅等人引入AHP 法确定权重，尽管考虑了评价指标实际的重要程度，但结果易受主观因素干扰。胡国强等人基于最小相对信息熵原理将主、客观权重结合起来，构建组合权重修正了邱玉婷等人和刘玉梅等人存在的缺点[1-2]。因此借鉴胡国强等人的组合权重计算方法[3]，提出改进的TOPSIS-RSR 法综合评价数控机床质量。分别应用AHP 法和熵权法计算指标的权重，依据最小相对信息熵理论，并结合拉格朗日乘数法计算组合权重。在组合权重基础上，利用改进的TOPSIS 模型对数控机床质量进行评价，引入邱玉婷等人的相对贴近距离代替传统TOPSIS 模型的相对贴近度，使评价结果更加准确。最后通过RSR 法对改进的TOPSIS 法中的相对贴近距离的标准正态离差进行分档、排序，减少评价过程中的信息损失，科学的评价数控机床的质量。

2 数控机床质量评价指标体系的建立

数控机床质量评价指标体系的建立应以评价的完整度高、目的准确、可拓展性强等作为原则，张根保等人对数控装备质量评价指标进行了详细分析[4]，因此根据文献[4]确立数控机床质量评价指标体系。如表1所示。

表1 数控机床质量评价指标体系

3 数控机床质量评价指标权重的确定

3.1 评价指标原始数据预处理

现假设有m个待评价数控机床，每个机床分别有n个质量评价指标，第i个机床的第j个评价指标值为x(i，j)。

对评价指标数据矩阵进行标准化处理，统一所有评价指标的量纲。

对于成本型指标(指标数值越小越优)：

对于收益型指标(指标数值越大越优)：

3.2 层次分析法确定主观权重w1

层次分析法(AHP)是一种定性与定量分析相结合的多准则决策方法，可有效解决多因素复杂问题[5]。其具体求取过程见文献[3]，这里不再重复叙述。

3.3 熵权法确定客观权重w2

1)计算第i个机床的第j个指标的权重。

2)计算第j个指标的熵值。

3)计算第j个指标的熵权。

3.4 最小相对信息熵原理确定组合权重[6-9]

综合评价指标的主观权重w1和客观权重w2计算组合权重wk，k=1，2，3，，…，n。显然wk与w1和w2都应尽可能接近，根据最小相对信息熵原理可知：

用拉格朗日乘数法优化可得组合权重计算公式：

4 改进的TOPSIS-RSR综合评价法

4.1 改进的TOPSIS法(逼近理想解排序法)

TOPSIS法的基本思想是构造正、负理想解，并以距正理想解最近且距负理想解最远的目标作为最优解[10]。传统TOPSIS 法是通过单纯的比例公式即式(8)来计算相对贴近度Ci，对数控机床质量进行综合评价。这种评价方式有一定的缺陷，如图1所示，假设a代表正理想解，b代表负理想解，c，d，e分别代表三个数控机床评价目标，且线段ce垂直平分线段ab。因此易知c，d，e到正理想解a和负理想解b的距离相等，即=，=，=。因此由式(8)可以计算出c，d，e三个数控机床评价目标的相对贴近度Ci=0.5，但是c，d，e到正负理想解的距离不同，即≠≠≠≠。此时无法对它们的优劣性进行区分。

图1 TOPSIS缺点描述

本文采用邱玉婷等人提出的一种改进的TOPSIS 法[1]，以相对贴近距离Di代替相对贴近度Ci，Di的计算公式如式(9)所示。通过比较评价目标与最理想参照点的距离，等权重地考虑了各评价目标与最理想参照点的相对接近度，以修正上文提出的传统理想解法的缺点。

4.2 改进的TOPSIS-RSR综合评价法应用步骤

4.2.1 改进TOPSIS法与RSR(秩和比)法结合的合理性分析

RSR 法广泛地应用于多指标综合评价、统计质量控制等方面[11]，是一种粗略的参数估计方法，应用参数统计的思想对评价目标进行分档、排序。应用RSR法进行评价时，会抛弃指标数据的信息，并会掩盖两个评价个案在某个评价指标上的微小差别，导致评价结果不准确。改进的TOPSIS法中的相对贴近距离Di是利用原始数据矩阵正向化和标准化之后的统一量纲矩阵计算得到的，能够较好的反映指标数据的信息。因此，利用TOPSIS-RSR 法对数控机床质量进行评价分析能够获得较为准确的结果。

4.2.2 应用步骤

1)运用AHP法、熵权法分别求出数控机床评价指标的权重，根据式(7)计算组合权重。

2)利用改进的TOPSIS 法求出相对贴近距离Di。具体求解过程见文献[1]，这里不再叙述。

3)对Di值进行编秩。因为Di为低优指标(值越小越优)，因此从小到大编秩。

4)计算RSR值。计算频数f，累计频数∑f。秩次R，平均秩次R。向下计算累积频率P=/n。根据《百分数与概率单位对照表》[12]，将累计频率P换算为概率单位Probit，Probit为百分率P对应的标准正态离差u+5[13]。

5)以相对贴近距离Di为因变量，概率单位Probit为自变量用MATLAB的cftool工具箱拟合出一次线性回归方程。

6)分档归类。根据评价对象数量，一般可分为3～5挡，也可根据组间方差F 值大小，选择分档数，并评价各档间差异[14]。根据线性回归方程计算临界Probit值对应的临界Di值，从而对各数控机床评价目标的Di值进行分档、排序。常用的分档数及对应的概率单位临界值见文献[10]。

5 实例分析

为了验证该方法的实用性和评价的准确性，引用文献[15]的5个数控机床的原始样本数据进行分析，数据如表2所示。

表2 数控机床评价指标原始数据[15]

1)表2中的购买价格、定位精度、重复定位精度、最小分辨率、平均故障维修时间、故障率、换刀时间是成本型指标，用公式(1)进行标准化[16]。进给速度、主轴最大转速、使用可用度、平均故障间隔时间是收益型指标，用公式(2)进行标准化[16]。引用张根保等人的专家判定矩阵作为AHP法的评价指标判定矩阵[4]。根据AHP法的一致性判断条件CR＜0.1，对判断矩阵进行一致性检验：一致性指标CI=0.0651，一致性比例CR=0.0428＜0.1，因此判断矩阵一致性检验合格。

经计算，AHP法的评价指标权重向量为：

W1={0.2326，0.1327，0.0765，0.1807，0.0830，0.0621，0.0246，0.1085，0.0267，0.0359，0.0368}

熵权法计算的评价指标权重向量为：

W2={0.0977，0.2015，0.112，0.133，0.0012，0.1145，0.0001，0.136，0.007，0.2015，0.0017}

由式(7)计算得到的评价指标组合权重向量为：

Wk={0.1720，0.1866，0.1056，0.1769，0.0115，0.0962，0.0015，0.1387，0.0050，0.970，0.0089}

2)根据改进的TOPSIS 法计算数控机床评价目标的相对贴近距离结果见表3。

表3 改进TOPSISI法评价结果

数控机床评价目标的Di值越小，质量越优。由表3可知，数控机床质量的排序结果为：个案1＞个案3＞个案2＞个案5＞个案4。

3)以相对贴近距离结合RSR 法，按照文4.2.2 节步骤3、4求出Di值对应的概率单位值Probit，结果见表4。

表4 相对贴近距离分布

4)以相对贴近距离Di为因变量，概率单位Probit为自变量用MATLAB 的cftool 工具箱拟合出回归方程，如公式(10)和图2所示。

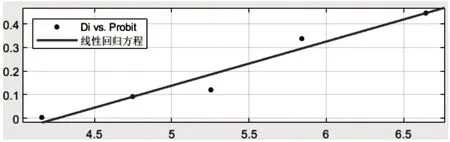
图2 线性回归方程

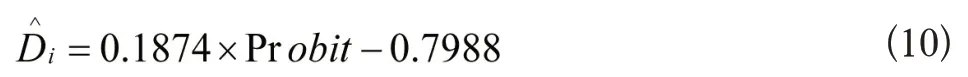
5)因为有5个数控机床评价目标，所以将质量分成1-5五个等级，其中1 级最优，5 级最差。根据文4.2.2 节步骤6的常用的分档数及对应的概率单位临界值，通过式(10)计算得到五个等级对应的临界相对贴近距离。再根据表3求出的数控机床个案的相对贴近距离进行等级划分。如表5所示。

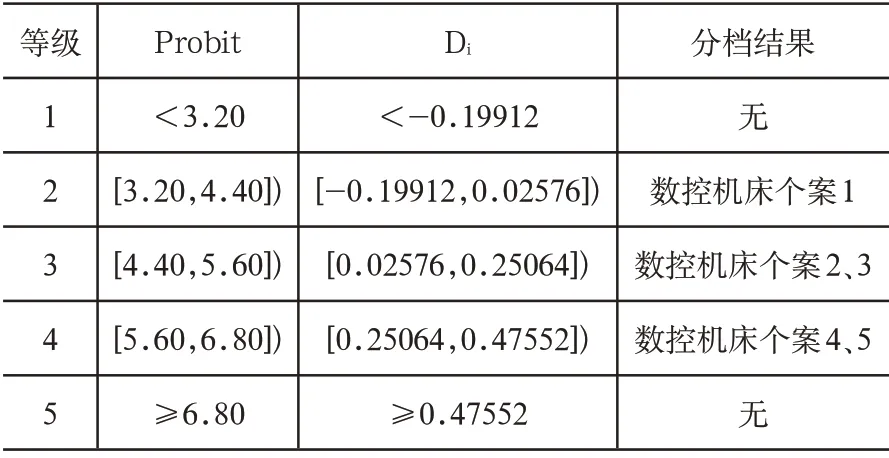
表5 改进的TOPSIS-RSR法数控机床质量分档结果

结合表3数控机床个案的Di值和表五的分级结果可知，1号机床的综合质量最好，2号机床、3号机床次之，4号机床的综合质量最差，与参考文献[4]、[16]的研究结果基本一致。由此可见，基于改进TOPSIS-RSR 法的数控机床质量评价模型是可行的。相比于文献[16]基于PP模型的数控机床质量综合评价方法，具有模型简单，原理清晰，工程实用性强的特点。

6 结束语

数控机床质量评价是一个综合性问题。考虑数控机床质量特征指标的实际价值量，参考专家经验，应用AHP法得出评价指标的主观权重。考虑到特征指标的变异性水平，应用熵权法确定客观权重。基于最小相对信息熵理论和拉格朗日乘子法计算组合权重。在组合权重的基础上，应用改进的TOPSIS-RSR 法获得数控机床质量综合评价结果。最后通过现实案例和与其他评价方法结果的对比证明了该方法是可行的。为数控机床质量评价提供了一个切实可行的方案。