基于核密度估计的重载组合列车纵向载荷谱外推研究
2022-04-26胡李军
胡李军,薛 海,周 宇
(兰州交通大学 机电工程学院,兰州 730070)
随着我国重载货运技术的发展,以及大功率交流传动电力机车、无线重联同步操作控制、大轴重、轻质铝合金车体以及3辆货车为一个固定单元、两端采用旋转式自动车钩、货车中间采用牵引杆连接等新技术的应用,货物运输由目前5 000-7 000 t的普通单元货运列车,提升为1万t重载单元或组合列车,重载化已成为铁路货运的发展趋势[1-2].纵向载荷谱作为重载列车关键技术基础性研究方向之一,表征了载荷大小与出现次数之间的关系,是重载列车整车和关键承载部件结构设计、安全评估和维修策略制定的理论基础.
由于受测试条件、经济成本、技术手段等因素限制,目前重载组合列车纵向载荷谱的外推方法是将雨流矩阵乘以测试里程的倍数,实现频次上的增加[3-5],而未充分考虑线路条件、机车操纵、载荷工况等不确定性因素,缺少纵向载荷及其出现次数在数理统计层面的特性表征,准确度较差.此外,载荷谱中小载荷的出现次数占总次数的大多数,而大载荷出现次数较少,有限测试里程的载荷数据不遵循均值服从正态分布、幅值服从威布尔分布的假定[6],从而使得在谱级数选取不合理的情况下,存在载荷谱拟合效果差、多级载荷段表征不连续、极值载荷确定样本不足等问题.针对上述重载组合列车纵向载荷谱外推存在的问题,结合目前铁路重载化发展趋势,以某线路1万t重载组合列车为研究对象,对数据分布形式不需要假定的条件下,运用核密度估计的非参数统计方法进行载荷谱外推,建立高表征度的重载组合列车纵向载荷谱.
1 纵向载荷特性分析
重载组合列车在牵引、启动、制动调速、进站停车期间,车辆之间存在着拉伸或压缩运动,产生的纵向载荷通过车钩缓冲装置进行传递.由于重载组合列车采用非刚性的自动车钩,且钩体尾部弧面与从板球形弧面之间有一定的活动间隙,存在垂向和横向运动.为获得较为准确的纵向载荷,通过在钩体钩身位置处沿纵向粘贴多组应变片筛选中性层的方法制作测力车钩,以此排除横向载荷和垂向载荷的影响.试验车辆为由117辆C80型铝合金敞车组成的1万 t运煤重载列车,从控机车位于第60辆货车前部.
根据纵向载荷频谱特性和信号采集相关理论,设置采样频率为500 Hz.图1为测试某一趟的重车和空车纵向载荷-时间历程,可知:不同工况下纵向载荷呈非对称性,且在空、重车条件下,最大拉伸载荷分别为733 kN和1 224 kN,最大压缩载荷分别为637 kN和1 030 kN,均方根值分别为153 kN和362 kN,重车时的纵向载荷大于空车的载荷;若取车钩材料E级钢的疲劳性能参数m值为4,则空、重车纵向载荷所造成的损伤占比分别为88.2%和11.8%,说明重车时的纵向载荷是造成重载组合列车部件损伤的主要原因.

图1 纵向载荷-时间历程Fig.1 Longitudinal load-time history
采用雨流计数获得纵向载荷-时间历程的雨流矩阵,分级数取为128级,统计分析纵向载荷均值与幅值的概率分布特性,结果如图2所示.

图2 载荷概率统计Fig.2 Probability statistics of load
取显著性水平α=0.05,将所有均值分成k个互不重迭的小区间,每个小区间的频数记作ni,根据式(1)获得总体样本落入第i个区间的概率pi,进而依据式(2)对均值是否符合正态分布进行χ2非参数假设检验.
(1)
(2)
式中:ai-1、ai分别是第i个区间的左、右端点;μ为总体样本的均值;σ为总体样本的标准差;n为样本总数.
2 载荷的非参数统计
由于重载组合列车纵向载荷受机车操纵、空重车状态、线路条件、运行工况等因素的影响较大,综合比较多种载荷谱外推方法,采用基于核密度估计的非参数统计方法外推,一方面该种方法不依赖样本的具体分布形式,可以克服纵向载荷分布呈现的不规则特性,获得较好的统计稳健性,另一方面统计结果高度依赖有限的样本,可以全面地反映多种影响因素导致的结果分散性,得到与实际情况相符的结果[7-9].
采用雨流计数法,对纵向载荷-时间历程进行编谱,得到相应的均值-幅值(Fm-Fa)二维雨流矩阵.由于在连挂车辆间存在着相对的拉伸-压缩运动,根据纵向载荷作用方向的不同,依据式(3)~(4)分别获得拉伸载荷FL和压缩载荷FY为:
拉伸载荷:
(3)
压缩载荷:
(4)
由于在同一车位、不同测试下雨流矩阵的各级载荷不相等,不易实现各次数对应维度元素的叠加计算,为此,考虑载荷均值对结构损伤的影响,根据疲劳累积损伤理论和材料的S-N曲线,通过Goodman公式修正载荷幅的方式计算各级载荷所造成的结构损伤占比di为:
(5)
式中:Di为修正的载荷幅Fa1i造成的结构损伤;DZ为载荷造成的结构总损伤;Ni为Fa1i对应的出现次数.
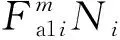
(6)
式中:h为带宽;K(·)为选取的核函数;nj为测试次数.
由于带宽取值的大小决定了核密度估计函数的平滑程度,影响估值的结果.为此,采用积分均方误差(MISE)进行最佳带宽的选取,其表达式为:
(7)
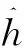
(8)
(9)
在损伤一致的条件下,保证总损伤不变,通过改变前后各级载荷对应损伤的缩放修正,可实现修正的载荷幅Fa1与所造成结构损伤Di的关系表达式,使其具有通用性.与此同时,依据式(4)~(9),可获得总损伤DZ的概率分布.
由于较大载荷是造成重载组合列车承载部件损伤的主要原因,为此,在不同概率对应的载荷谱外推过程中,需要确定载荷的最大值.考虑载荷波动连续性对载荷最大值的影响,通过载荷数据的分组整合进行倒序排列,分别提取同一车位、不同测试雨流矩阵中出现1次的载荷,提取截至到出现次数为2次的载荷,采用核密度估计的方法,依据式(4)~(9),可获得载荷谱中最大级载荷的概率分布.
设概率P对应获得的最大级载荷为FmaxP,谱级数为NP,总损伤为DZP,则外推所得载荷谱中各级载荷对应次数Ni的表达式为:
(10)
式中:f(·)为载荷幅Fa1与造成的结构损伤Di的关系表达式.
3 纵向载荷谱的外推
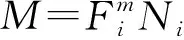
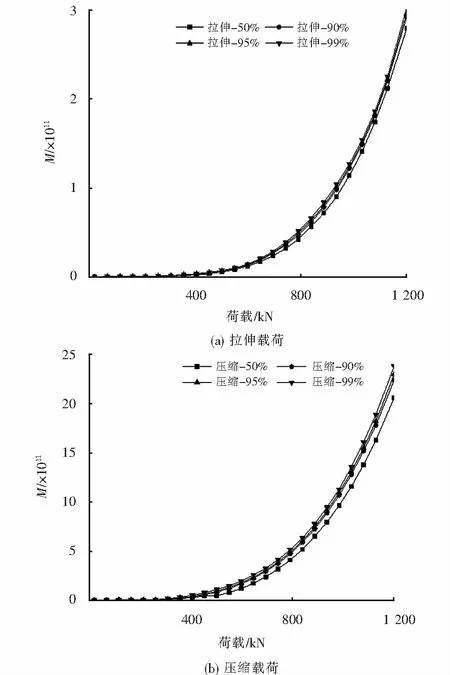
图3 不同概率下的载荷-损伤关系Fig.3 Load-damage relationship under different probabilities
对比分析多种曲线拟合模型,采用表达式(11)所示的一元高次多项式模型,进行载荷与所造成损伤关系曲线拟合的效果较佳,从而定量分析不同概率下载荷-损伤关系,结果如表1所示.采用优度系数对拟合效果进行检验,其中99%概率下拉伸载荷-损伤拟合效果最差,为0.914,所有拟合值都接近1,说明拟合效果较好.

表1 不同概率下的载荷-损伤关系表达式系数
D(F)=A0F4+A1F3+A2F2+A3F+A4.
(11)
分别选取各测试次数对应的总谱级损伤,采用核密度估计的方法,获得拉伸载荷和压缩载荷所造成的损伤概率分布曲线,结果如图4所示,以50%概率对应的谱级损伤为基准,得到50%、90%、95%和99%概率下, 拉伸载荷对应的总谱级损伤比为1∶1.23∶1.29∶1.39,压缩载荷对应的总谱级损伤比为1∶2.02∶2.14∶2.37.同理,可获得拉伸载荷和压缩载荷最大值的概率分布曲线.

图4 损伤的核密度估计分布Fig.4 Damaged nuclear density estimation distribution
根据式(10)得到不同概率下载荷-次数-谱级损伤的关系.图5为50%、90%、95%和99%概率下载荷-次数-损伤关系曲线,从中得出:随着载荷的增加,外推的载荷和次数同时发生了变化,且次数变化差异性不大,但所造成的损失呈指数级增加.
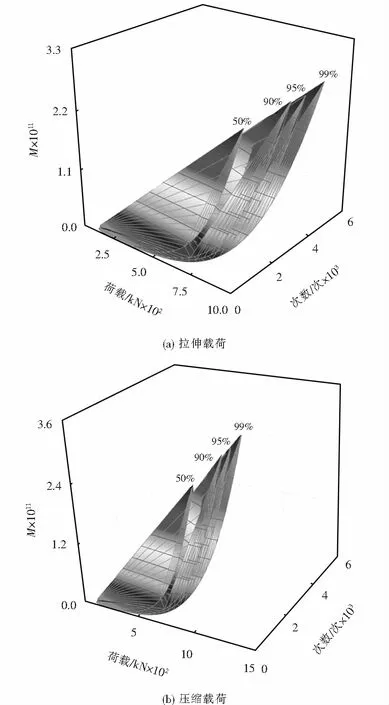
图5 载荷-次数-损伤的关系Fig.5 Load-time-damage relationship
取载荷大于1 000 kN的谱级,得到50%、90%、95%和99%概率下所外推的载荷-次数关系如图6所示,从中得出:随着统计概率的增加,载荷和次数同步增加.
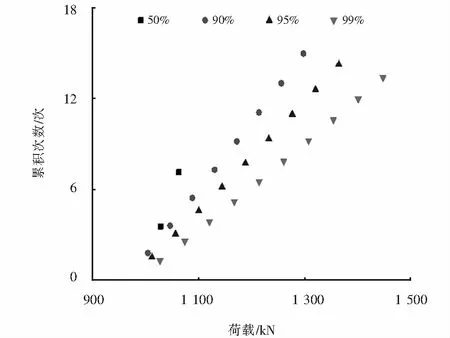
图6 载荷-次数关系Fig.6 Load-time relationship
4 外推载荷谱的等效变换
在重载组合列车承受纵向载荷的结构设计时,根据结构的重要程度选取不同的可靠度,从而需确定相对应概率外推下的载荷谱,当谱级数选取过多,降低了设计效率,不宜用于结构设计.在开展重载列车结构纵向疲劳试验时,设备可施加的载荷受其技术参数的制约,考虑试验时间和成本的因素,需要在充分利用试验设备的同时尽可能减少试验次数.为此,在保证损伤一致性的前提条件下,需要对不同外推概率下的载荷谱进行等效变换.根据式(10),在保证损伤不变的情况下实现载荷-次数的变换.
图7取最大载荷为1 063 MPa时,等效变换所得到的不同概率下的载荷-累积次数关系曲线,从中得到:50%、90%、95%和99%概率下,取编谱公里数为测试公里数的100倍,则拉伸载荷的次数分别为425、516、525、581次,压缩载荷的次数分别为186、372、389、429次,而当载荷次数统一取为2次时,对应的拉伸载荷分别为642、673、677、693 kN,压缩载荷分别为928、1 103、1 116、1 144 kN,从而通过缩减次数、增加载荷的方式实现载荷谱的等效变换.
从图7可以看出,在90%、95%和99%概率下外推的结果与原测试载荷(概率50%)下的趋势基本一致,较好的保留了测试载荷的分布特征,且外推获得了不同概率下大、中载荷对应的循环次数,相对于线性外推方法具有明显优势.
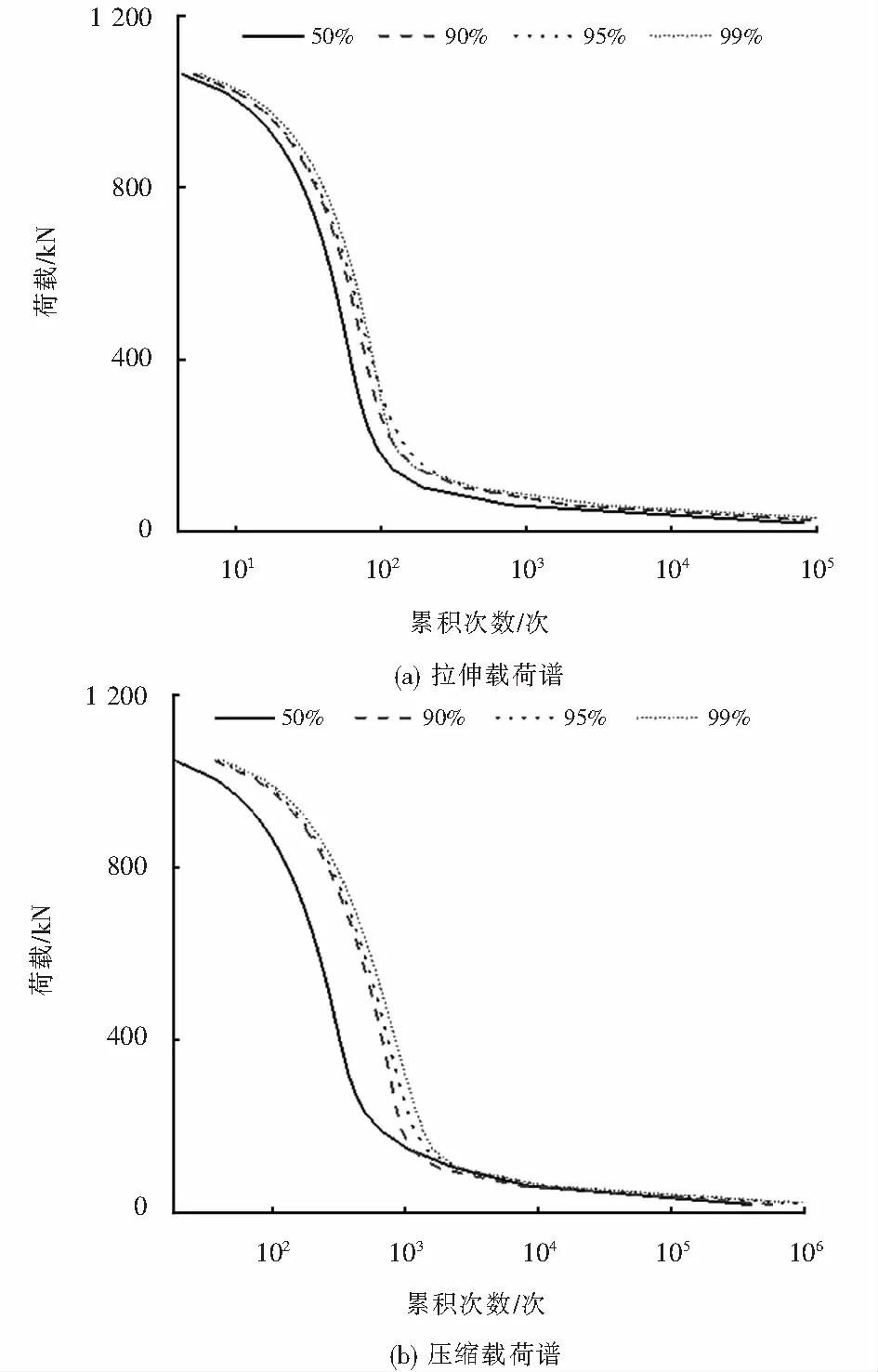
图7 外推载荷谱的等效变换Fig.7 Equivalent transformation of extrapolated load spectrum
5 外推载荷谱的验证
为验证上述所得不同概率下外推载荷谱的有效性,目前所采用的方法主要有统计参数检验、拟合度检验、疲劳损伤检验等[13-14].由于载荷谱是进行结构疲劳设计和疲劳试验的前提,同时也是制定疲劳规范和安全评定的基础,为此,选用疲劳损伤检验的方法进行1万t重载组合列车纵向载荷谱外推有效性的验证.由于纵向载荷-时间历程是通过测力车钩获得,为此,以车钩为验证对象.
根据参考文献[15]得,车钩拉伸载荷和压缩载荷的应力转换系数分别为0.36 MPa/kN和0.14 MPa/kN,车钩材料E级钢的疲劳极限δe=143.8 MPa,所对应的疲劳寿命为2×106次,疲劳性能参数m值取为4,考虑车钩疲劳性能的分散性,通过数理统计和曲线拟合获得99.5%可靠度下的P-S-N曲线为:
S4·N=8.55×1014,
(12)
根据结构疲劳损伤理论,得到第i级载荷对应循环次数ni下的车钩疲劳损伤为:
(13)
式中:Fi为第i级等效载荷,f为应力转换系数.
依据表达式(13),得到拉伸载荷谱和压缩载荷谱在车钩服役100万km对应的损伤计算结果见表2.
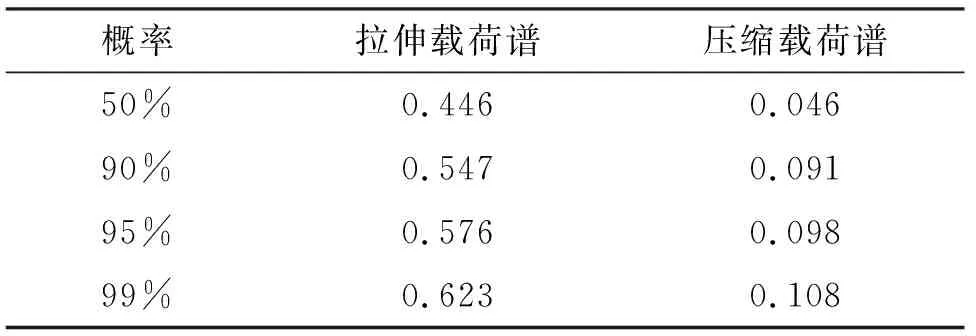
表2 不同概率下的载荷总损伤对比结果
结合表2和图7可以得出,随着外推概率的增加,较大载荷循环产生的次数明显增多,造成的累积损伤也随之增加.与概率为50%的结果相比,在概率为99%的情况下,拉伸载荷谱所造成的总损伤是50%概率对应损伤的1.40倍,压缩载荷谱所造成的总损伤是50%概率对应损伤的2.35倍,与载荷谱外推理论实际情况相符,从而证明了外推结果的有效性.
6 结论
1) 采用核密度估计的非参数统计方法,建立不同概率下载荷谱的外推,在保证结构损伤一致的条件下,不依赖样本的概率分布可通过各级损伤的缩放修正,实现不同概率下载荷-次数-谱级损伤关系的外推,并根据实际情况实现载荷谱的等效变换.
2) 随着外推载荷谱中载荷的增加,各级纵向载荷所造成的结构损伤呈指数式变化,且大载荷级造成的损伤占比较大,而在不同的外推概率下,小载荷区载荷级所造成的损伤差异性较小.
3) 通过不同概率下外推结果,可以得出随着概率的增加,外推获得了较多低周、较大载荷,外推概率99%下的拉伸载荷谱疲劳损伤损伤比实际测试的增加40%,压缩载荷谱增加135%.为此,在载荷谱编制时有必要获得可能出现的较大载荷.
4) 根据结构所受载荷特点,可将基于核密度估计的纵向载荷谱外推方法,推广应用到其他轨道车辆装备零部件载荷谱的外推,以此考虑载荷分散性的前提条件下,实现高表征度纵向载荷谱的外推.
