基于预滤波器和两级AIME的GNSS/INS超紧组合慢变故障检测

刘士明，李四海，郑江涛，付强文，陶渊博

1.西北工业大学 自动化学院，西安 710072 2.中国兵器工业导航与控制技术研究所，北京 100089

卫星/惯性组合导航可以一定程度上弥补卫星导航系统(GNSS)和惯性导航系统(INS)独立使用的缺陷。在已有的组合形式中，GNSS/INS超紧组合在不良信号环境中具有明显的性能优势，得到了研究人员的广泛关注。由于采用了矢量式跟踪架构，超紧组合中未被检测到的故障会在跟踪通道间传播。因此同松组合和紧组合相比，故障对超紧组合的影响更为严重。在所有的故障类型中，小变化率的慢变故障是最难检测的一类故障。慢变故障在开始时幅度比较小，需要累积较长的时间才有可能被检测到。对于超紧组合系统而言，减小慢变故障的检测时间，有助于抑制故障在通道间的相互传播，能够极大地提升系统的鲁棒性。

GNSS/INS组合系统通常利用Kalman滤波器实现状态的最优估计。Kalman滤波器的状态方程和量测方程为故障检测提供了解析余度信息。因此基于Kalman滤波器的故障检测方法在GNSS/INS组合导航领域被广泛采用。

多解分离法是一类重要的完好性监测(RAIM)方法。Honeywell公司利用多解分离法设计了一种GPS/INS紧组合系统的完好性监测算法。Rockwell Collins公司提出了一种归一化解分离故障检测方法。多解分离法是一种单历元检测方法，对慢变故障的检测存在较大延迟。而且这类算法包含多个子滤波器，计算效率不高。

Kalman滤波器的量测新息可以衡量量测和状态估计的一致程度。基于新息序列的故障检测是另一类重要的组合导航故障检测方法。新息卡方检验法利用单历元新息向量构造故障检测统计量，对突变故障有很好的检测效果，但是对慢变故障的检测并不十分有效。利用多历元新息序列构造检测统计量是检测慢变故障的一种有效方法。Litton公司提出的AIME(Autonomous Integrity Monitored Extrapolation)方法是一种最为经典的多历元新息检测方法。文献[13]对比分析了解分离法和AIME 2种方法，表明AIME方法对慢变故障的检测更有效。文献[14]使用AIME故障检测量的变化率作为检测量，能够明显减小慢变故障的检测时间。文献[15]把AIME方法和最小二乘支持向量机结合起来，提升了GPS/INS紧组合系统对慢变故障检测的实时性。基于AIME的改进方法还应用在GNSS/INS组合系统的欺骗干扰检测中。

虽然对GNSS/INS松组合和紧组合的故障检测已经进行了大量研究，但是目前针对深组合和超紧组合故障检测的研究还比较缺乏。文献[17]利用惯导信息辅助标量式深组合系统检测伪距粗差和多径引起的伪距偏差。文献[18]提出了一种利用滑模微分速率检测器检测深组合慢变故障的方法。文献[4]研究了GNSS矢量式接收机的完好性监测问题。文献[19]提出了一种基于预滤波器的超紧组合故障检测方法，但是并未披露算法的实现细节。文献[20]通过对矢量接收机的架构进行改进，提升矢量式接收机的RAIM性能。

GNSS/INS超紧组合有相干式和非相干式等多种不同的实现形式。超紧组合系统的故障检测应当充分利用其具体的实现架构，以达到更好的故障检测效果。本文针对包含预滤波器的GNSS/INS非相干超紧组合系统，提出了一种减小慢变故障检测时间的新方法。由于预滤波器专属于跟踪通道，而且新息序列的采样率更高，因此更适合于故障通道的检测和隔离。基于经典的AIME算法，设计了一种基于预滤波器的两级AIME故障检测方法。第1级AIME检测基于预滤波器实现，并且构造关于第1级AIME检测统计量的单状态Kalman滤波器。第2级AIME检测基于这个单状态Kalman滤波器实现。仿真结果表明，新方法可明显减小慢变故障的检测时间，并且能够有效抑制故障在跟踪通道间的传播。

1 GNSS/INS非相干超紧组合模型

在GNSS/INS非相干超紧组系统中，相关器输出的相干积分结果首先输入到码和载波鉴别器，获得环路跟踪误差参数。有关鉴别器的详细内容可以参考文献[23]。

码鉴别器和载波频率鉴别器得到的跟踪误差，转换为伪距和伪距率残差作为导航Kalman滤波器的量测。

(1)

需要注意的是，鉴别器更新频率通常高于组合滤波器的量测更新频率。为了降低噪声，应采用平均的方式而不是上采样的方式，把高采样率的鉴别器输出转换为低采样率的量测。

(2)

式中：为鉴别器更新频率和组合滤波器量测更新频率的比值。

超紧组合Kalman滤波器采用如下17维的状态向量,包括惯性导航误差，惯性器件测量误差和接收机时钟误差。

=

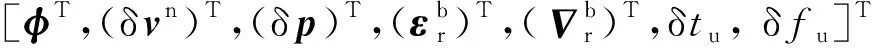
(3)

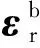
组合Kalman滤波器的离散时间动态模型为

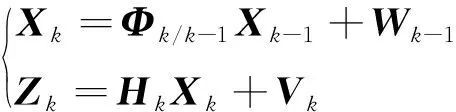
(4)

式中：下标表示当前历元；-1表示上一历元；-1为状态转移矩阵；为量测矩阵；-1和分别为系统噪声向量和量测噪声向量。状态转移矩阵和量测矩阵与常规紧组合滤波器相同，详细内容可以参考文献[10,25-26]。

组合滤波器量测向量为

=

(5)

2 基于预滤波器的慢变故障检测

2.1 AIME故障检测方法

Kalman滤波器的量测新息定义为真实量测和量测预测值之差，可表示为

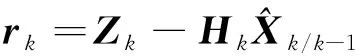
(6)

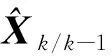
根据Kalman滤波的基本理论，当系统无故障时，新息序列是零均值的高斯白噪声序列，其协方差矩阵为

(7)

式中：-1为状态一步预测均方误差矩阵；为量测噪声方差矩阵。

AIME算法的检测统计量定义为

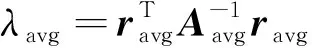
(8)

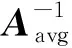
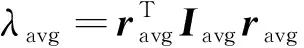
(9)

新息序列加权平均值和其信息矩阵由如下信息融合公式给出:

(10)

(11)

式中：表示用于新息序列平均的历元数。

当无故障时，服从自由度为的中心卡方分布，为量测维数(即新息的维数)。当存在故障时，服从自由度为的非中心卡方分布。检测门限根据系统虚警率设定，二者的对应关系为

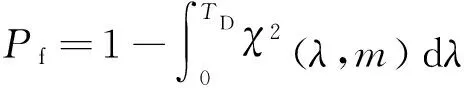
(12)

2.2 基于预滤波器的AIME

非相干超紧组合系统的一种典型实现是在每个通道配置一个通道预滤波器。预滤波器的量测更新频率通常高于组合滤波器。在不采用数据比特擦除的情况下，以GPS L1 C/A码信号为例，相干积分时间是20 ms，预滤波器的量测更新频率是50 Hz。因此利用通道预滤波器进行故障检测，有利于缩短故障检测时间。另外，每个通道的预滤波器在形式上是相互独立的，在检测到故障的同时也实现了故障通道的识别与隔离。

通道预滤波器包含3个状态参数，码相位误差，载波频率误差和载波频率误差的变化率δ。预滤波器的离散时间系统模型为

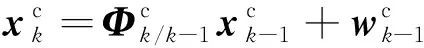
(13)

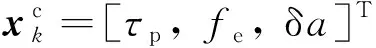
状态一步转移矩阵为

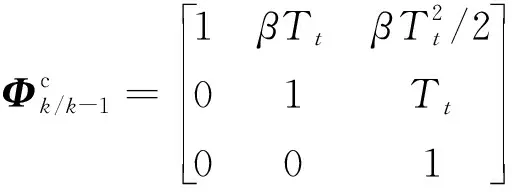
(14)

式中：为时间更新周期；=为转换系数；为伪码码率；为标称载波频率。

预滤波器量测模型为

(15)

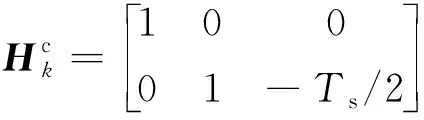
(16)

式中：为预滤波器的量测更新周期。

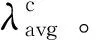
超紧组合系统利用惯导信息计算得到本地复制信号的控制参数。惯导信息的精度直接决定了环路跟踪误差和预滤波器的量测精度。因此惯导精度对基于预滤波器的故障检测依然有着至关重要的影响。

2.3 慢变故障的影响分析

存在慢变故障时，系统量测模型可表示为

=++

(17)

式中：为慢变故障向量。

不失一般性，假设故障从=1时开始，慢变故障存在时新息序列的期望为

(18)

式(18)等号右边第1项是当前故障向量，第2项表示历史故障的影响，其中,+1的具体形式为

(19)

式中：=+1(-)；为单位矩阵。

在标准Kalman滤波中，增益计算回路不受滤波计算回路的影响，慢变故障存在时的新息协方差矩阵和式(7)相同。

在式(18)中，等号右边的2项通常不能相互抵消，即新息序列不再是零均值的时间序列。此外可以看出，当前历元的故障向量直接影响同一时刻的新息期望。历史故障对新息期望的影响是逐步累积的，通过状态转移矩阵、量测矩阵和增益矩阵的组合进行传递。

对于标准Kalman滤波，在滤波达到稳态后，滤波增益阵会趋近于数值很小的稳态值。由于增益阵的衰减，历史故障对当前新息向量的影响也相对减弱。式(18)中当前故障占据主导作用,新息期望的绝对值将逐渐增大。此时，AIME检测量服从非中心卡方分布，非中心参数为

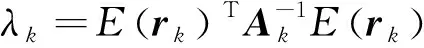
(20)

新息期望绝对值的增大导致非中心参数增大。AIME检测统计量会出现逐渐增大的趋势(受噪声和历史故障的影响非严格单调递增)，在文献[13-15]中也可观察到这种变化趋势。另外，即使故障变化率很小，AIME通过长时间的平均也可以减小平均新息的协方差从而使得检测统计量增大。

3 基于预滤波器的两级AIME检测算法

根据2.3节的分析可知，如果采用标准的Kalman滤波器，一般情况下，当存在慢变故障时，AIME的检测统计量随时间呈现出逐渐增大的趋势。与之相反，在不存在慢变故障时，检测统计量则不会出现递增趋势。图1展示了在无故障和伪距慢变故障2种情况下，AIME故障检测统计量的典型变化趋势，其中慢变故障从第100个检测历元开始引入。

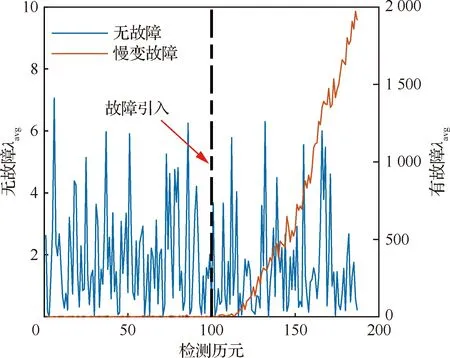
图1 AIME故障检测量的典型趋势Fig.1 Typical trends of AIME test statistics

合理地利用检测量的递增变化趋势，可以减小慢变故障的检测时间。这里提出一种基于预滤波器的两级AIME故障检测方法，以加快对慢变故障的检测。

首先，为每个跟踪通道设计一个关于预滤波器AIME检测量的Kalman滤波器，以下简称为检测量Kalman滤波器。各通道的检测量Kalman滤波器独立运行，每个检测量滤波器只包含一个状态变量。因为在无故障时，检测量不会出现大幅度的变化，因此把检测量建模为一个随机游走过程。滤波器的离散时间状态方程为

=-1+-1

(21)

滤波器量测为2.2节中预滤波器使用AIME方法计算而得的检测统计量，量测方程为

=+

(22)

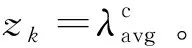
系统噪声本质上是检测量变化扰动白噪声，噪声方差设置为10。采用一种基于Allan方差的量测噪声自适应方法，实时确定量测噪声方差。

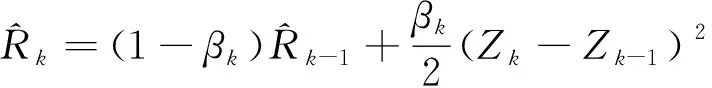
(23)

(24)

式中：初始值=1；衰减因子0<<1，通常取=09～0999。

由前文分析可知，当存在慢变故障时，检测量逐渐增大。对于检测量Kalman滤波器而言，递增的检测量，也可以视为存在慢变类型的故障。因此基于检测量Kalman滤波器再次使用AIME故障检测方法。

检测量Kalman滤波器的量测新息为

(25)

新息方差为

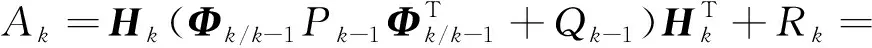
-1+-1+

(26)

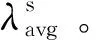
检测量Kalman滤波器的状态和量测均为标量，在计算过程中不涉及矩阵计算。和其他AIME改进方法相比，具有实现方式简单以及计算效率高的优点。

在预滤波器中使用的AIME故障检测被称作第1级AIME故障检测。相应地，检测量Kalman滤波器中的故障检测被称作第2级AIME故障检测。这种使用两次AIME进行慢变故障检测的方法被称作基于预滤波器的2级AIME故障检测方法，其工作流程如图2所示，图中的、和为预先设置的固定值。

在两级AIME故障检测中，第1级AIME检测量不再直接用于故障检测，而是作为检测量Kalman滤波器的量测，真正用于故障检测的是第2级AIME检测量。由于第1级AIME不直接用于故障检测，因此这种方法并不会导致故障检测的虚警率增高。

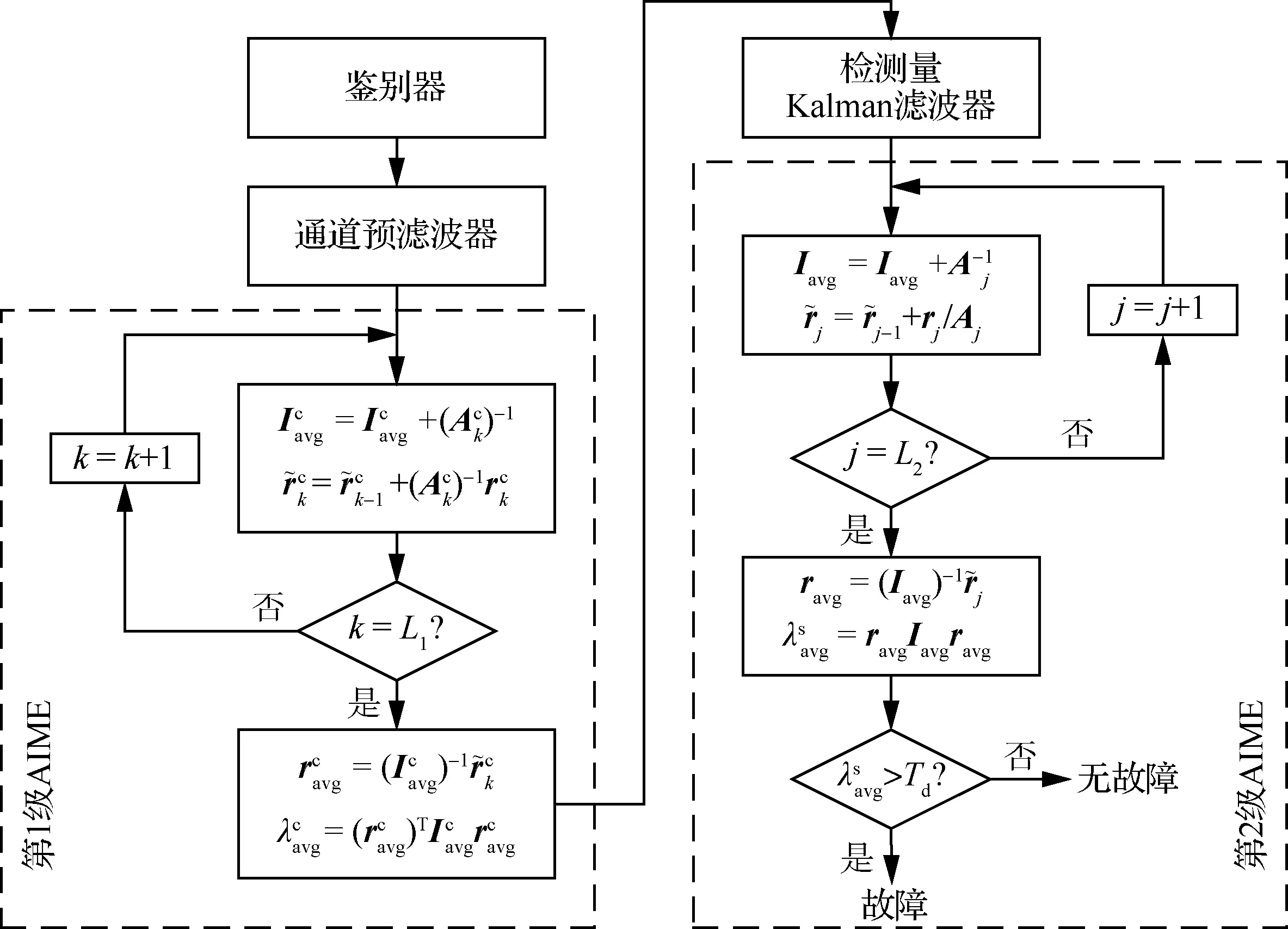
图2 基于预滤波器的两级AIME算法流程Fig.2 Flow diagram of two-stage AIME algorithm based on prefilters

4 仿真结果与分析

利用计算机仿真试验的方法评估本文所提出的故障检测方法的检测性能。对比分析了3种故障检测方法：基于组合滤波器的AIME故障检测(以下简称为M1)、基于预滤波器的AIME故障检测(以下简称为M2)和基于预滤波器的两级AIME故障检测(以下简称为M3)，对伪距慢变故障的检测性能。仿真的故障场景包括单星故障和2星故障2种场景。

4.1 仿真设置

利用一条仿真的运动轨迹作为参考轨迹，基于参考轨迹产生卫星导航信号与IMU测量数据。仿真轨迹的总时长为250 s。载体三维运动轨迹和运动速度分别如图3和图4所示，最大加速度为6 m/s。仿真过程中可见卫星的伪随机码(PRN)编号为：1，3，11，17，19，22，28，30。

仿真轨迹输入高性能卫星导航信号模拟器产生射频信号。射频前端把射频信号转换为数字中

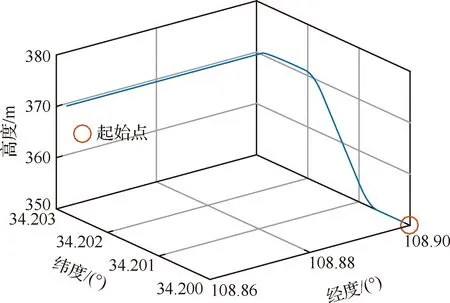
图3 仿真参考轨迹Fig.3 Simulation reference trajectory

图4 仿真载体运动速度Fig.4 Velocity of simulation vehicle

频信号并存储在计算机上。在卫星导航信号模拟器中可设置伪距的故障类型和大小。此外，基于仿真轨迹产生惯性测量单元(IMU)的陀螺和加计数据。仿真中所采用的IMU误差参数见表1。

表1 IMU仿真误差参数Table 1 IMU simulation error parameters

最后，以数字中频信号和IMU数据作为数据源，利用基于软件接收机的GNSS/INS超紧组合仿真系统进行后处理仿真分析。在仿真程序中，软件接收机跟踪环路的相干积分周期设置为20 ms，因此通道预滤波器的量测更新频率是50 Hz。组合滤波器的量测更新频率设置为1 Hz。

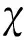
M1和M2的新息平均时间设置为20 s，对应的平均历元数分别是20和1 000。M3中第1级AIME新息平均时间设置为2 s，第2级AIME的新息平均时间设置为10 s。

4.2 单星故障仿真结果

首先考虑单颗星伪距慢变故障，从70 s开始引入慢变故障，选择PRN17为故障卫星。由于对变化率1 m/s以上的慢变故障，经典的AIME方法已经有很好的检测效果。因此这里只考虑小变化率的慢变故障，变化率分别为0.05 m/s，0.1 m/s，0.2 m/s和0.5 m/s。首先在强信号环境下进行仿真分析，载噪比设置为48 dB·Hz。

图5为故障变化率0.05 m/s时的检测统计量对比。可以看出M1方法的故障检测统计量始终小于故障检测门限，因此没有能够检测到故障的存在。与之相反，M2和M3方法均成功检测到了故障。在70～100 s，3种方法的检测统计量均没有明显的增长。在100 s之后，M3检测统计量的变化率明显高于M2检测统计量的变化率。M3在故障注入57 s后检测到故障存在。M2故障检测时间约为 85 s。

图6对比了故障变化率0.05 m/s时3种方法的归一化新息，归一化新息的定义参考式(27)。由于M1和M2的新息是矢量，选择和故障直接相关的新息分量构建归一化新息。对于M1，选择对应于伪距残差的新息分量。对于M2，选择对应于码相位误差的新息分量。M3的归一化新息对应于第1级AIME的故障检测统计量。

(27)

从图6可以看出，M3的归一化新息明显大于其他2种方法，因此M3的故障检测时间远小于M1和M2。虽然M1的归一化新息略大于M2，但是M2对应的新息序列采样率更高，有助于故障的累积。因此M2的故障检测时间小于M1(在仿真中M1没有检测到故障)。表明提高新息序列的采样率和构建幅值更大的归一化新息均有助于加快慢变故障的检测。

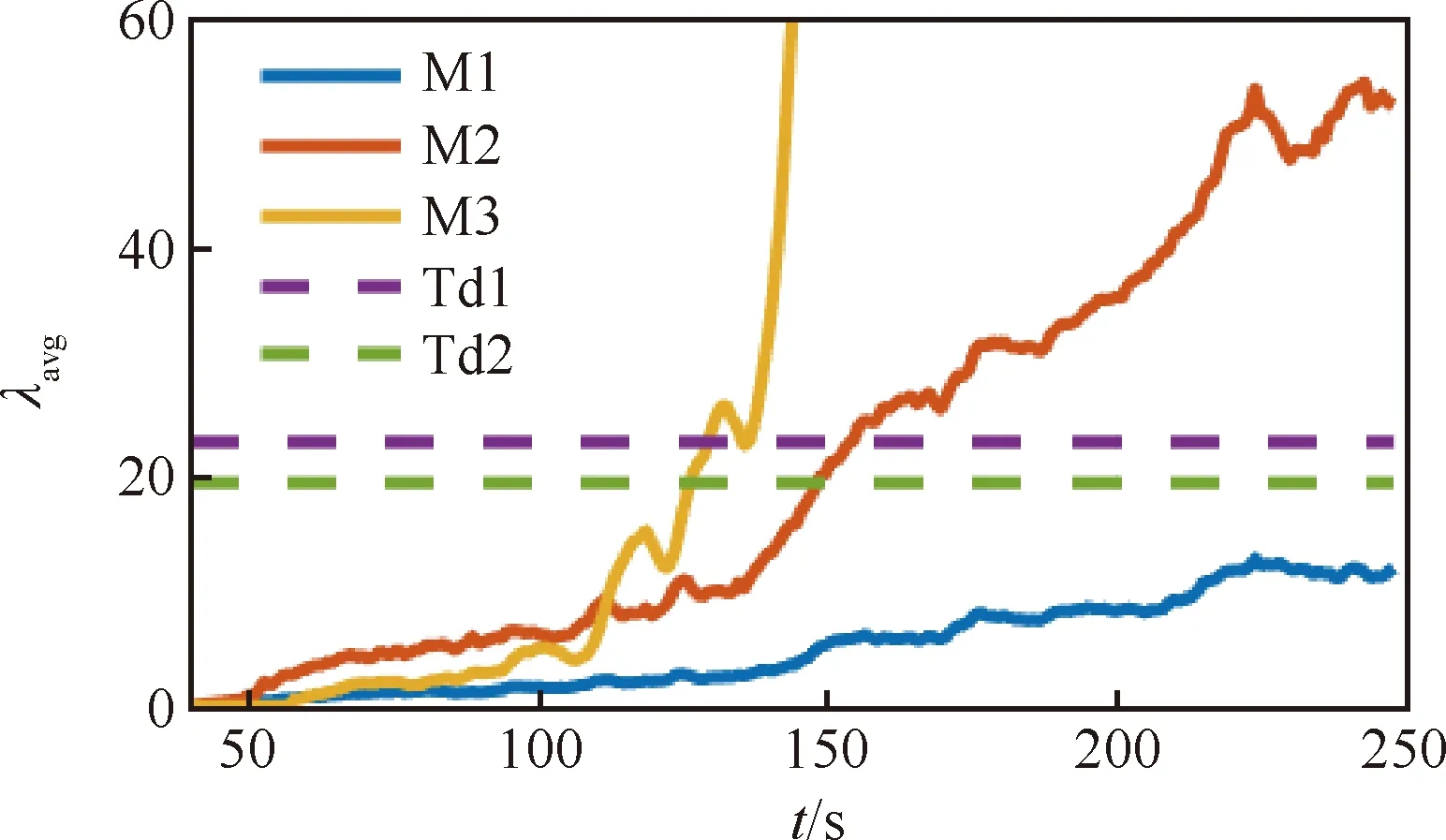
图5 故障变化率0.05 m/s时检测统计量Fig.5 Test statistics for faults with a rate of 0.05 m/s

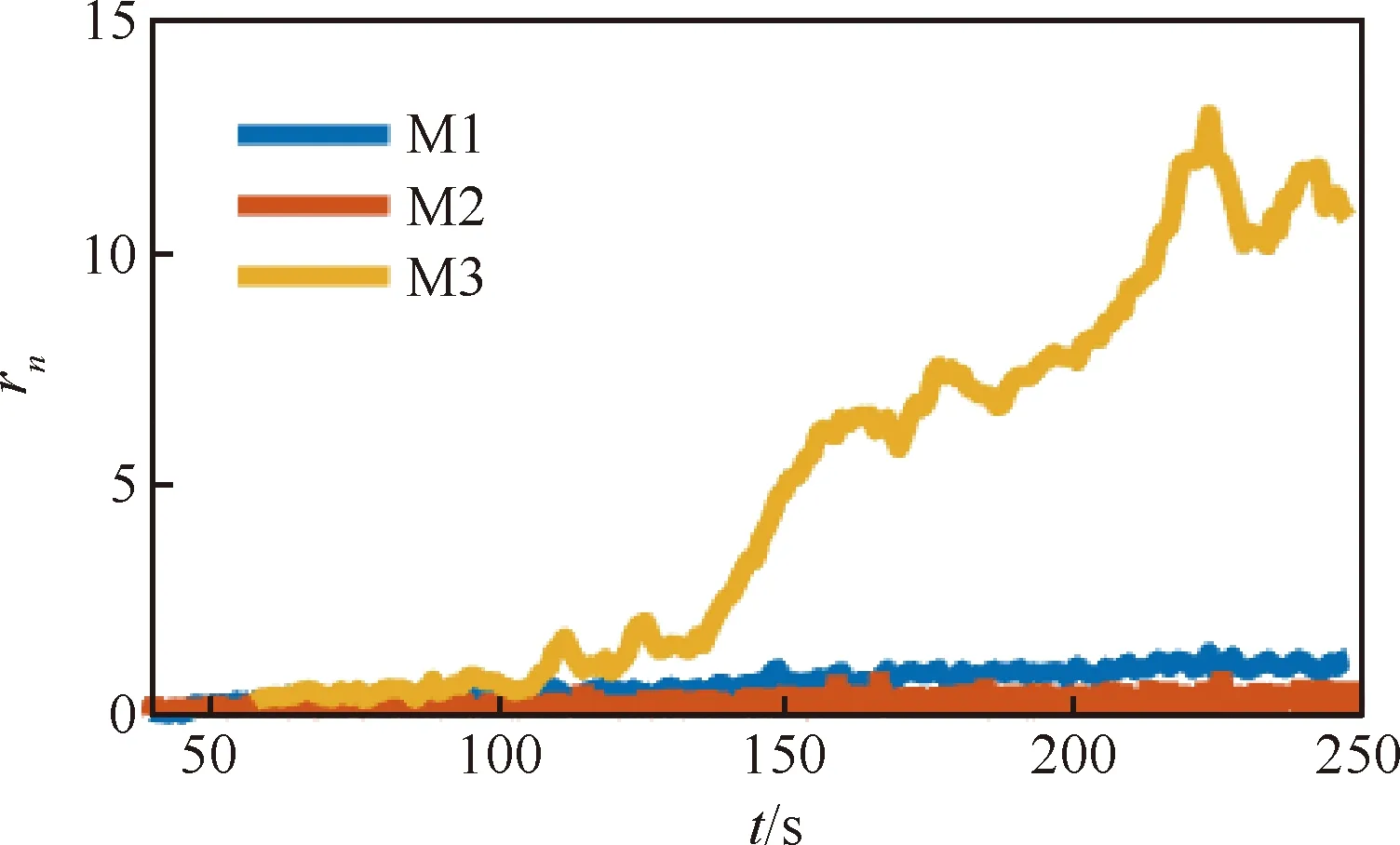
图6 归一化新息Fig.6 Normalized innovations

图7展示了故障变化率0.1 m/s时3种方法的检测统计量。M2的检测时间约为57 s，M3的检测时间约为41 s。虽然M1方法可以检测到故障的存在，但是其检测时间约为154 s，远大于M2和M3的检测时间。

对应于故障变化率0.2 m/s的检测统计量如图8所示。M1的故障检测时间约为72 s。M2的故障检测时间约为44 s。M3的故障检测时间约为35 s。和前面的仿真结果相比，由于故障变化率的增加，故障检测时间相对减小。

图9为故障变化率0.5 m/s时的检测统计量对比。M1的故障检测时间约为41 s。M2的故障检测时间约为25 s。M3的故障检测时间约为19 s。3种方法的检测时间依然是M1最大，M3最小。但是和前面的仿真结果相比，3种方法在故障检测时间上的差异明显减小。

为了更准确地对比3种方法的慢变故障检测时间，进行了100次蒙特卡洛仿真，平均检测时间如图10所示。在仿真时间内，M1未能检测到0.05 m/s的慢变故障，因此图中没有显示M1对于0.05 m/s的慢变故障的检测结果。3种方法中，M1的故障检测时间最长，M3的故障检测时间最小。而且从图中还可以明显看出，故障变化率越小，M3在故障检测时间上的优势越明显。

图7 故障变化率0.1 m/s时的检测统计量Fig.7 Test statistics for faults with a rate of 0.1 m/s

图8 故障变化率0.2 m/s时的检测统计量Fig.8 Test statistics for faults with a rate of 0.2 m/s

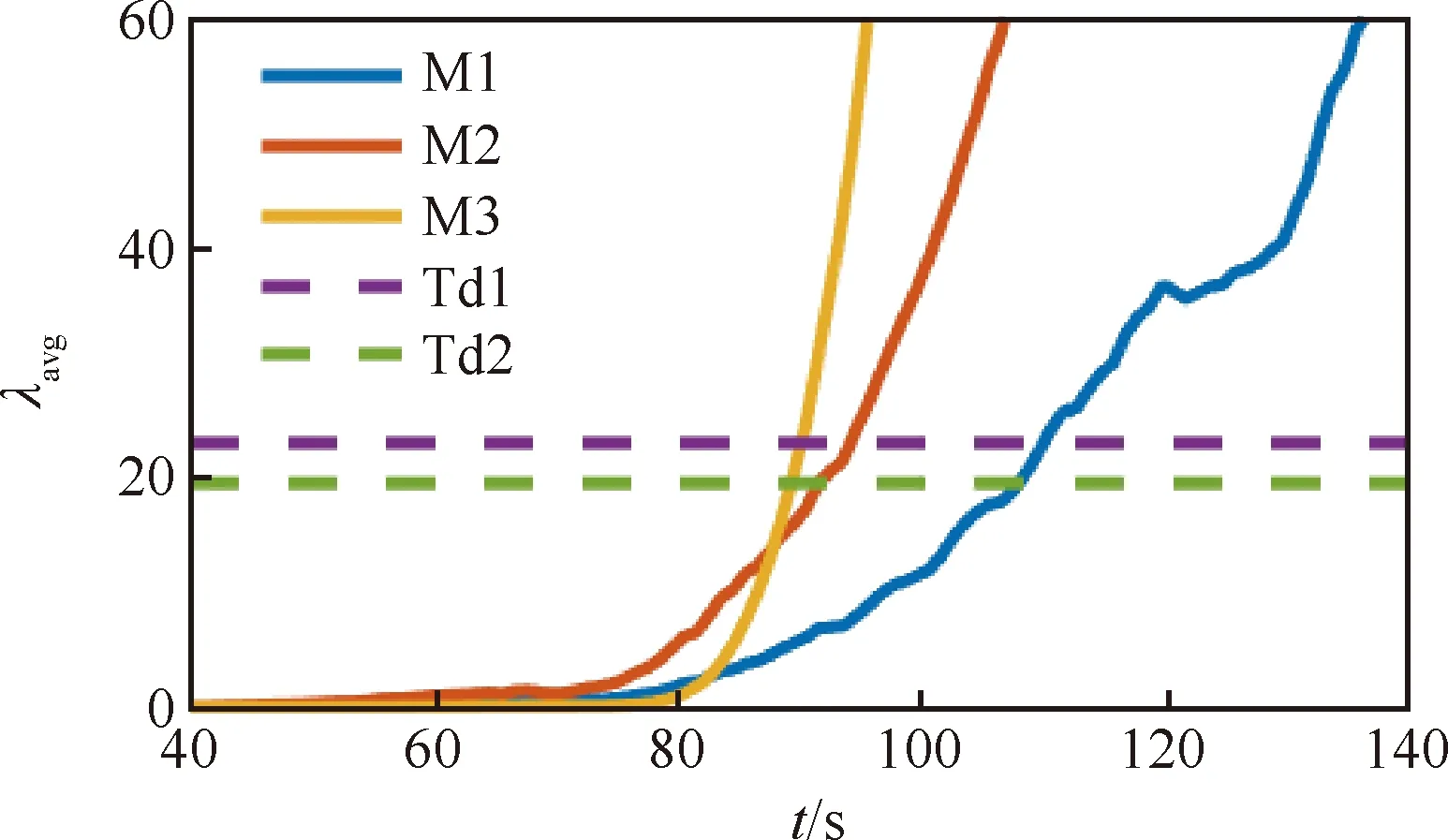
图9 故障变化率0.5 m/s时的检测统计量Fig.9 Test statistics for faults with a rate of 0.5 m/s

接下来评估在弱信号环境中的检测性能，信号载噪比设置为28 dB·Hz。表2为100次蒙特卡洛仿真结果(保留整数)，其中“-”表示没有检测到故障。可以看出，三者中检测时间最小的依然是M3。此外弱信号环境中量测噪声增大，检测时间明显滞后于强信号环境中的仿真结果。

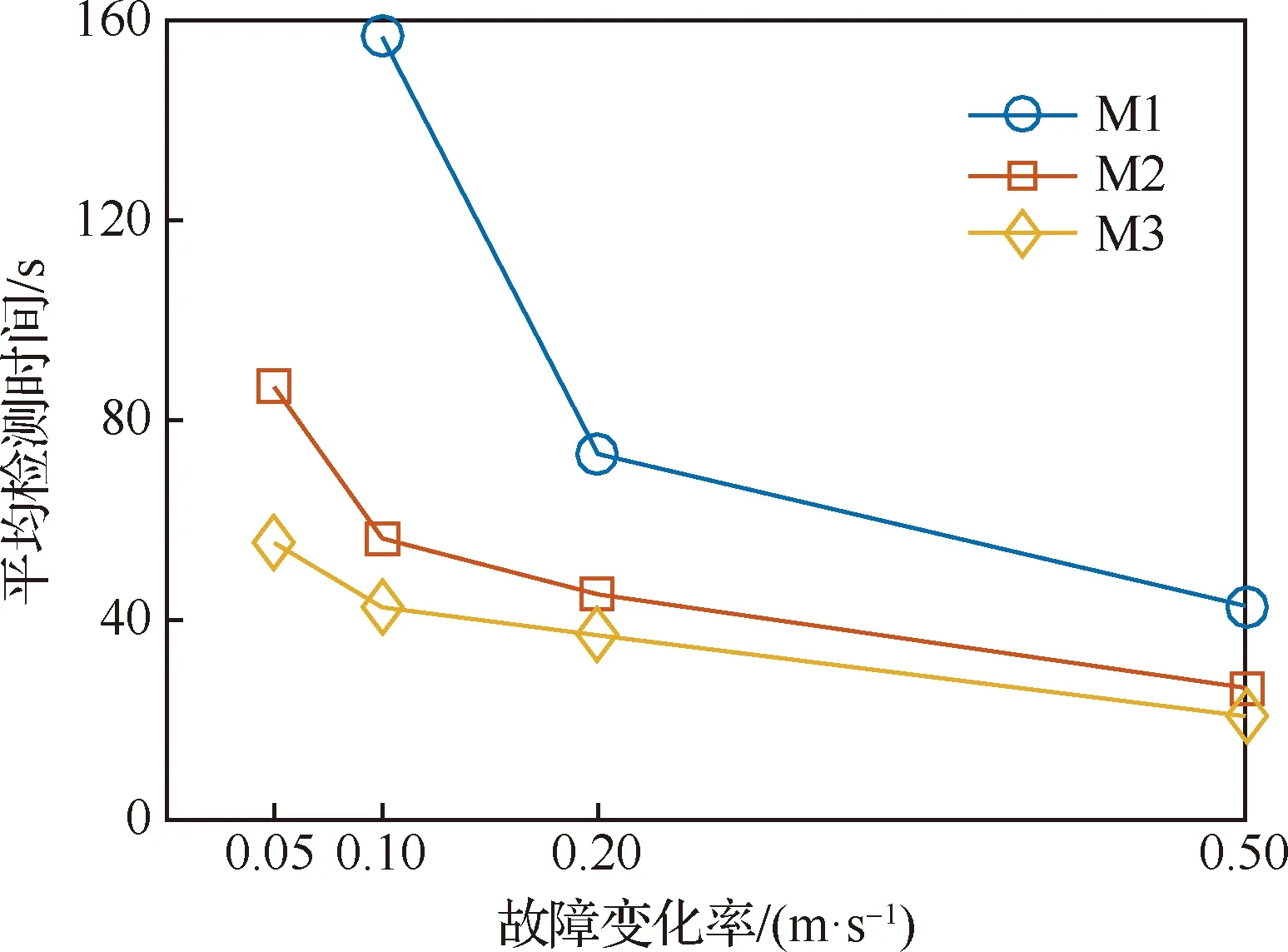
图10 慢变故障平均检测时间Fig.10 Average detection time for slowly growing faults

表2 弱信号环境下的检测时间Table 2 Detection time in weak signal environment

4.3 两星故障仿真结果

本节验证在2颗星同时发生慢变故障时的检测性能。和4.2节相同，依然是在伪距上加入慢变故障，故障开始时间为70 s。故障卫星编号为PRN17和PRN28。2颗星的故障变化率均设置为0.1 m/s。载噪比设置为48 dB·Hz。

图11为M3对全部8颗可见卫星的故障检测统计量。在无故障时(70 s之前)，全部卫星的故障检测量均为小量。在70 s之后，PRN17和PRN28的故障检测统计量迅速增大并超过故障检测门限。而其他无故障卫星由于第1级AIME检测统计量没有增长趋势，所以第2级故障检测量继续保持为很小的值。说明在两颗星同时发生小幅度慢变故障的情况下，基于预滤波器的两级AIME的方法能够正确识别故障卫星。

下面对比分析M1、M2和M3对2颗星故障的检测时间。图12和图13分别为PRN17和PRN28的故障检测统计量。对于PRN17，M1在仿真时间段内未能检测到故障存在。M2的故障检测时间是88 s。M3的故障检测时间为48 s。对于PRN28，M1在仿真时间段内也未能检测到故障存在。M2的故障检测时间是98 s。M3的故障检测时间是55 s。对于2颗卫星，M3的故障检测时间都是最小的。而且和单颗星故障仿真结果相比，M3和M2在故障检测时间上差异更大，即M3的优势更加突出。另外，和单颗星故障相比，两颗星故障时的检测时间更长。主要原因是，存在两颗故障星时，伪距故障对组合导航解的影响更大，滤波器的误差跟踪效应更强，导致故障

图11 基于预滤波器的两级AIME检测统计量Fig.11 Test statistics of all visible satellites based on prefilters and two-stage AIME method

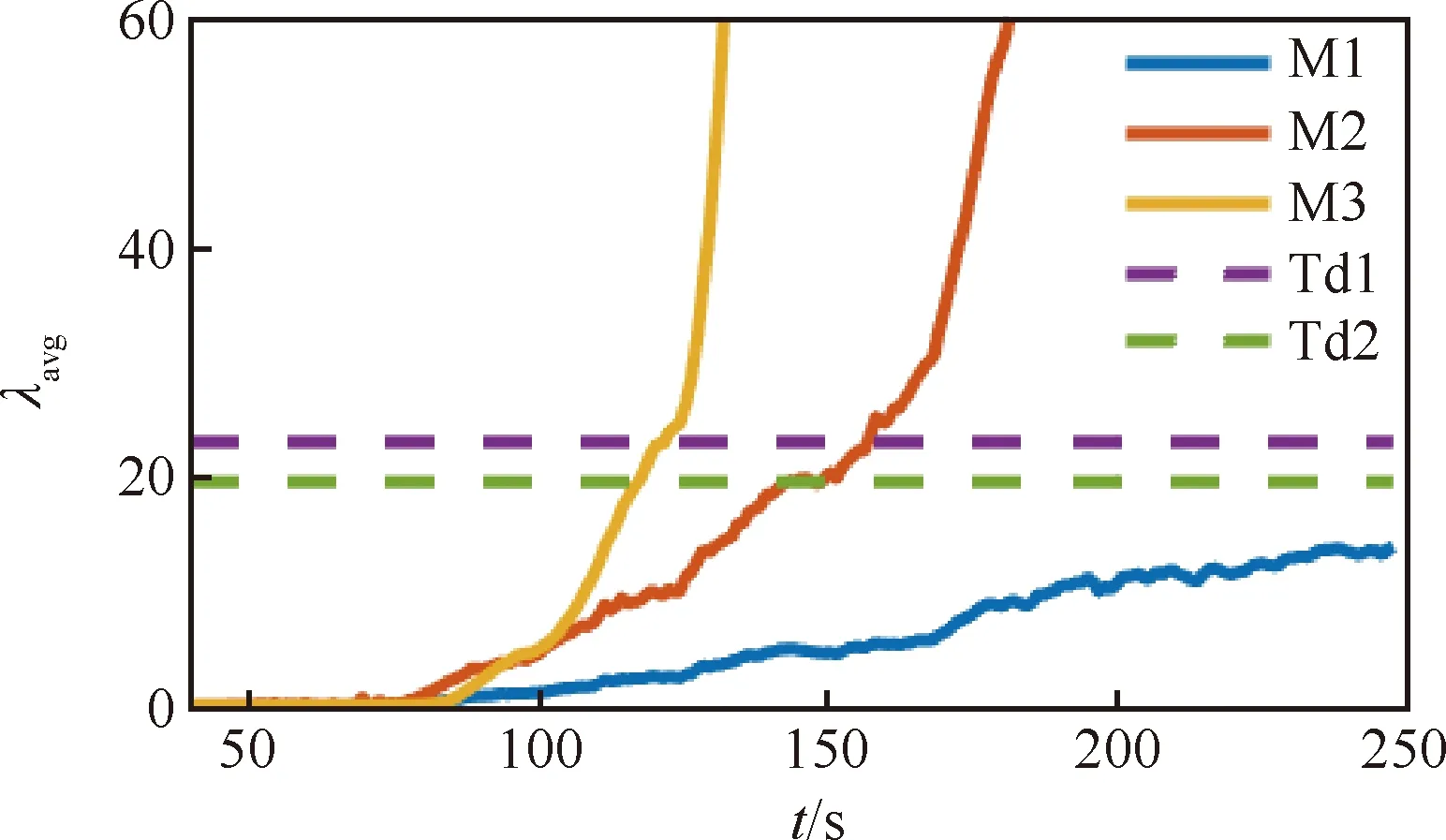
图12 PRN17的故障检测统计量Fig.12 Fault test statistics for PRN17

图13 PRN 28的故障检测统计量Fig.13 Fault test statistics for PRN 28

检测时间相对延长。

图14和图15分别为使用M2和M1时，所有可见卫星的检测统计量。从图14可以看出，由于使用M2时故障检测时间较长，在100 s之后，除2颗故障卫星外，无故障卫星的检测量也稍有增加，说明故障已经传播到其他正常跟踪通道。而使用M1时，由于不能隔离故障通道，故障对正常通道的影响更加严重。在图15中，PRN03和PRN19的检测统计量明显增大。对比图11、图14和图15可以看出，由于能减小故障检测时间，及早隔离故障通道，M3可有效抑制慢变故障在跟踪通道间的传播。

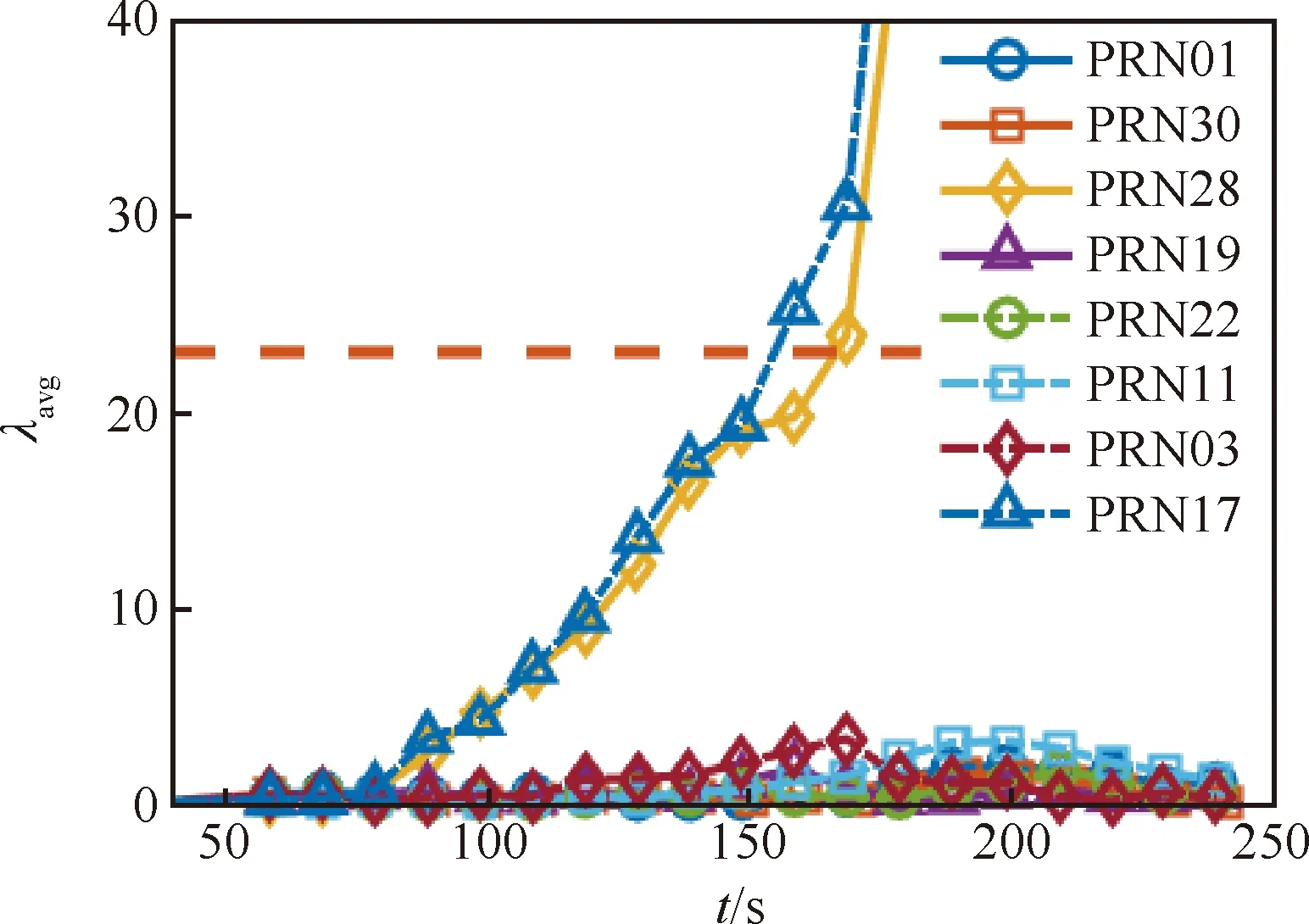
图14 基于预滤波器的AIME全部可见星检测统计量Fig.14 Test statistics of all visible satellites based on prefilters and AIME method

图15 基于组合滤波器的AIME全部可见星检测统计量Fig.15 Test statistics of all visible satellites based on integration Kalman filter and AIME method

5 结 论

1) 针对一种GNSS/INS非相干超紧组合架构，提出了一种基于预滤波器的两级AIME慢变故障检测方法，重点关注小变化率(小于1 m/s)慢变故障的检测。在单星故障场景下，对3种故障检测方法进行了对比分析。仿真结果表明，在存在慢变故障时，所提方法具有最大的归一化新息和最小的故障检测时间。从蒙特卡洛仿真结果来看，故障变化率越小，所提方法在检测时间方面的优势越明显。

2) 对于两星同时发生故障的场景，新方法能够正确识别故障卫星，并且故障检测时间也是3种方法中最小的。和单星故障相比，两星故障对组合导航解的影响更大，导致两星故障的检测时间大于单星故障的检测时间。由于能及早检测到故障卫星，新方法可有效抑制故障在跟踪通道间的相互传播。

目前未考虑稀疏可见星情况，可见星数目对所提故障检测方法的影响还需要进一步研究。