从误到悟：指向数学运算素养培养的教学策略探讨——以“三角函数”习题课为例

文∣陈姗姗

《普通高中数学课程标准(2017年版)》把数学运算定为六大核心素养之一，数学运算是解决数学问题的基本手段。数学运算是演绎推理，是计算机解决问题的基础。实际教学中，数学运算的重要性得到了广大师生的高度认可，但是落实不够。尽管师生都知道运算非常重要，但却不愿意花时间和精力培养运算素养。主要原因不外乎两方面：一是混淆运算错误的归因，二是忽视从错误中得到启示。数学运算尤其是三角函数，涉及公式多，运算量大，学生常把精力放在记忆公式上，忽视对运算的要求。本文以三角函数习题课为例，探究培养学生运算素养的教学策略。

一、误的表现及原因

“误”的归因有很多，但不少学生习惯把运算错误归为“失误”，从而降低了对运算的要求。学习本来就是一个不断出错的过程，我们总是期待学生不要出错，这是不可能的。不回避错误，善待错误才能解决问题，学生的错误也是思维的一种体现。

(一)会而不对：运算对象不明确

考试结束后学生常常感到很懊恼，会而不对；也有学生会轻视这个问题，他们觉得这不是什么大问题，下次注意就行了；还有的学生会把丢失的分加到自己的分数中，认为自己应该考这么多分。这样的侥幸心理会导致学生在以后的学习中对运算的不重视。学生可以如此，但是教师却不能，教师应该针对学生的每一个错误进行剖析，引导其深刻的反思，“会”了什么，“不对”又是怎么造成的。例如已知同角三角函数sinα,cosα,tanα中的一个值求另外两个值的问题，该类问题要根据角的范围对三角函数的取值进行判断。但由于学生对运算对象理解不到位，会因不明确运算对象的具体意义而导致计算错误。准确理解运算对象是正确进行数学运算的必要条件，准确理解运算对象即学生通过阅读、审题，厘清题目情境、设问、条件与结论，正确表征题目的条件与结论，这是数学运算的重要环节，直接决定着数学运算质量的高低、效果的好坏，学生数学运算中的错误往往都是由此引起的。因此，培养数学运算的第一步就是明确运算对象。

大黄鱼体色按照国际发光照明委员会CIE（CIE,1976）的规定测定，L*代表亮度值、a*代表红色值、b*代表黄色值。使用CR-400型色彩色差计（柯尼卡-美能达，日本）于夜间20:00至24:00进行测定，避免外源性光照对大黄鱼体色的影响。每个网箱随机取5尾鱼，在背部和腹部皮肤分别选取2个点测定体色值，尽量保证检测部位的一致性。

(二)对而不全：运算法则不清晰

“对而不全”的现象比较严重，其主要原因是学生对知识一知半解，如概念模糊，公式记不全，定理不理解等。所有这些都会导致运算法则不清晰。

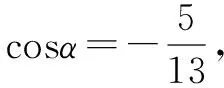
适当提早播种。山地油菜应在9月中、下旬播完，争取冬前长出较大的营养体，使其扎根深、早封行，从而提高抗旱能力。

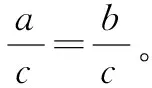
(三)全而不优：运算结果不严谨

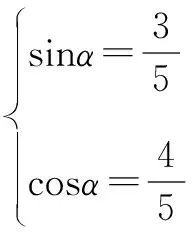
二、悟的内涵及策略

(一)悟本质：追本溯源

理解数学的本质是深度学习的前提，而理解数学既不能仅靠教师的讲解，也不能靠大量地做题，而是学生对数学对象本质的领悟。

按照管理和业务职能分开的原则，同时结合人影业务五段式业务流程，调整了市级人影部门内部机构，市级人影部门分为人工影响天气管理办公室和人工影响天气指挥中心，彻底结束了既当裁判员又当运动员的模式，完全实现管办分离，提升了工作效率。市局人影中心分为：综合保障股、业务管理股、预报与评估股、指挥调度股、飞机增雨股、飞行观测股、科研管理股、空域请示股、紧急联络股等。

讲解此类题时，并不是复述等式的性质，而是追问一句：为什么c≠0？从而找到问题的本质。

(二)悟方法：一题多解

对于同一道题，不同的学生会选择不同的方法来解答，每个学生观察问题的差异和观察问题的角度不同，而且知识储备不同。一题多解也恰好反映了不同知识点的魅力所在，实现知识点的融会贯通，实现知识的网络化，构建有效的知识体系。

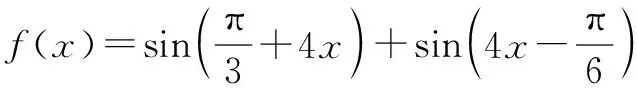
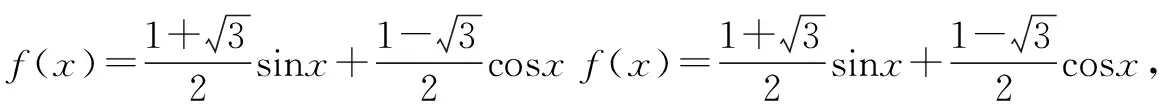
(三)悟规律：变式教学

欣竹走后，思雨就有些后悔，因为他当时想向欣竹要一根头发，然后把两根头发放在一起认真地比较一下，看看究竟是不是欣竹的长发。可当时他没有张开口。他也的确不知道怎么张口向欣竹要一根头发。思雨这么一想，竟然吓了一跳，如果这根长头发真的是欣竹的，那不更加麻烦了？在妻子面前就真的是跳进黄河洗不清了。但刚才看欣竹的头发时，又的确觉得那根长发丝跟欣竹的头发一样。那根长发丝如果真的是欣竹的，又怎么会沾到自己的毛衣上呢？同欣竹根本就没有过什么近距离的接触。他跟欣竹就是上下级的严肃关系，连手都没碰过。思雨觉得自己是越想越多了，应该先把这根头发搞清楚是谁的再说。找到了这根长发丝的主人，其他的事以后再说。

两天后，他带着丝缕的愧疚百分的底气给辛娜打了一个电话，彼时，两人缓解了冷战级别，建立了对话平台，此时，坐在沙发上百无聊赖的王树林突然灵感激发，产生了某种原始的亢奋。他拿起手机，拨通了辛娜的电话，满脑子是互信共建和共赢，满肚子是点火挂挡和起步。他太想证明自己有按时下课的能力了。

变式教学是数学教学中常用的教学方法，能有效培养学生的迁移能力，深受广大教师的欢迎。但是如果不从变式教学中悟出规律，是达不到以点带面效果的。

抗战开始以后，南京政府摒除社会力量，建立起统一的合作行政体系，将农业合作事业置于政府控制之下，形成对农业合作事业的强制性制度推进。在强制性制度安排之下，中国农业合作事业完全丧失发展的自主性，无论从发展模式、发展速度亦或业务经营等方面，均服从于政府的行政指令，农业合作组织也被作为政府推行经济政策，维护政治统治的工具之一。在此背景之下，早期农业合作事业的自助与互助性质丧失殆尽。迄今为止，对抗战以后农业合作事业及合作金融问题尚缺乏系统性研究，尤其是1946—1949年间的研究基本处于空白。通过探讨政府垄断模式下农业合作金融的兴衰变革，透视在强制性制度安排下，中国农业合作事业的被动发展历程。

不少学生苦恼听得懂课而不会做题，而此问题的根源是学生缺少“悟”。只有经过“悟”的过程，数学知识才能从课本转到自己的大脑，“悟”的过程也就是知识内化的过程，对信息加工储存的过程。教学过程中，教师要给学生“想”的空间，“悟” 的时间，“润”的氛围，让思悟数学落地生根。“悟”要如何做到？

变式3：已知sinα+sinβ+sinγ=0和cosα+cosβ+cosγ=0，则cos(α-β)的值是( )。

“不懂就问”是很多家长和教师给学生提的学习建议，但事实真的是这样吗？勤学好问是好的，但“问”能否代替“悟”呢？“悟”错误就是重组大脑中的信息，对信息再加工的过程。因此，要误中参悟、误中顿悟、误中省悟，以误促学。

这几道题均是人教版高中《数学》必修第一册中的题目，把教材中的题目以变式教学的形式串讲起来，真正做到用教材教，而不是教教材。通过变式的形式让学生逐渐悟出和差公式逆用的规律，达到举一反三的效果。

三、误到悟的原则及反思

在电解相关的实际生产中,可以根据不同生产目标,综合考虑以上各种情况来设计电解装置。所以,遇到电解相关的实际问题,在分析电解过程中离子迁移情况时要结合题给信息,进行综合分析。

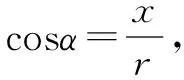
(一)误中参悟：关注运算对象的整体性

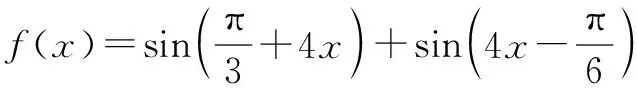
Alice (Bob)需要耗费4比特的经典信息将测量结果告知Bob(Alice)和Charlie,而Charlie需耗费2比特经典信息将测量结果告知Alice 和Bob,故本协议总的经典信息耗费为10比特。

(二)误中顿悟：寻找数学知识的联系性

数学是一个庞大的知识体系，所有的知识都不是碎片化的，而是有着千丝万缕的联系，掌握了知识之间的联系，才能形成稳固的知识网络。讲题时不能就题讲题，要能发散，也能归类。

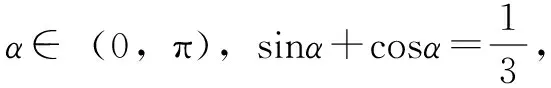
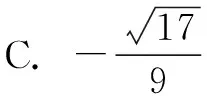
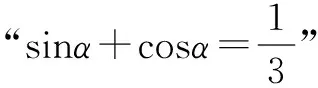
(三)误中省悟：探究解题方法的共通性

学数学的本质是学数学思想，数学知识随着时间会被遗忘，但是数学思想则不会，所以数学教学中要注重数学思想的渗透。通过不同的错误分析，探究不同的数学思想。常见的数学思想有分类讨论、数形结合、函数与方程、转化与化归。这些数学之间并不是独立的，而是相通的。

总是有学生抱怨考试时间不够用，其实运算占了很大的原因，学生不习惯对运算对象进行分析，总是希望一看就会，但是往往是一做就错。“磨刀不误砍柴工”，学生要舍得在分析运算对象、设计运算路径上下功夫，很多题目从条件到结论之间很难看出它们之间的联系，需要尝试、试错，然后不断地调整，在错误中参悟、顿悟和省误，才能逐渐走出误区。