基于模拟退火算法的人工势场法路径规划研究*

赵炳巍，贾 峰，曹 岩，孙 瑜，刘一鸿

(西安工业大学机电工程学院，陕西 西安 710021)

1 引言

近几年，得益于传感器技术、计算机科学和人工智能技术的快速发展，移动机器人在各个领域已受到广泛研究，并取得了巨大的进展。移动机器人对不同环境导航技术提出了更多的要求[1-3]。路径规划是移动机器人自主移动的核心技术之一。现有的路径规划方法主要分为传统规划方法和智能规划方法。传统规划方法主要有人工势场法和A*算法[4]等。智能规划方法主要包括遗传算法、粒子群算法、模糊控制法和神经网络等。其中，人工势场法有反应速度快、计算量小、便于实时控制和生成的路径平滑等优点，因此得到广泛应用[5]。

人工势场法原理是假设工作环境中存在虚拟势场力，目标点对移动机器人具有吸引力，而障碍物对其具有排斥力，这2种力的合力控制着移动机器人的运动。但是，人工势场法存在局部极小点的问题。为了解决此问题，国内外学者进行了大量的研究，Abadlla等[6]提出了一种改进的人工势场法与模糊逻辑法相结合的新方法。该方法克服了传统人工势场法局部极小点问题，提高了复杂环境下的导航性能,但未能完全克服机器人剧烈震荡问题。Mabrouk 等[7]引入移动机器人内部运动学主体状态方程，以解决传统人工势场方法的局部极小点问题。陈金鑫[8，9]等基于改进的势场函数，使用了增加控制力的方法来使机器人移出局部极小点区域，新的斥力势场函数把机器人与目标之间的相对距离也考虑进去，从而使目标点为整个势场的全局最小值点。Fazli等[10]采用沿墙避障算法来解决局部极小点问题，但是会相应地增加路径长度。程志等[11]引入机器人前进的方向向量，对斥力的生成和计算机制进行了调整，以解决其处于局部极小点情况下无法继续规划路径的问题。

针对传统人工势场法在路径规划中存在局部极小点，使得移动机器人无法达到目标点的问题,本文提出一种基于模拟退火法的人工势场法，利用模拟退火法在当前局部极小点的位置附近增设随机目标点，使移动机器人逐渐逃离出局部极小点区域。在Matlab上的仿真结果表明，此方法能够帮助移动机器人有效逃离局部极小点区域，达到目标点位置。

2 路径规划总体设计

路径规划是移动机器人执行导航和其他复杂任务的基础，其含义为查找从初始点到目标点的路径，并避免碰撞所有障碍物[12]。路径规划总体结构如图1所示。

Figure 1 Overall structure of path planning

移动机器人通过传感器采集系统，得出障碍物距离信息。基于障碍物信息，本文选用的路径规划方法为人工势场法，但其存在容易陷入局部极小点问题。因此，本文利用模拟退火算法，在局部极小点的位置附近，增设随机目标点，引导移动机器人逐渐逃离出局部极小点区域。基于模拟退火算法的人工势场法路径规划整体思路如图2所示。

Figure 2 Overall idea of path planning

3 传统人工势场法

3.1 基本原理

人工势场法是于1986年由Khatib首次提出的[13]。该方法将物理学中场的概念引入到路径规划中，其基本原理是将移动机器人假设成一个点，该点在一个虚拟力场中运动，虚拟力场由目标点对移动机器人的引力场和障碍物对移动机器人的斥力场组成。人工势场法的势场函数定义为引力场与斥力场的和，如式(1)所示：

U(X)=Uat(X)+Ure(X)

(1)

其中,X=(x,y)T为移动机器人的位置向量，Uat(X)为引力场，Ure(X)为斥力场。

势场函数的负梯度定义为人工力，其由引力和斥力组成。因此，移动机器人在势场中所受的力为引力和斥力的合力，如式(2)所示：

F(X)=Fat(X)+Fre(X)

(2)

其中,F(X)为所受合力;Fat(X)为引力，引导移动机器人走向目标点;Fre(X)为斥力，使移动机器人远离障碍物。其受力图如图3所示。

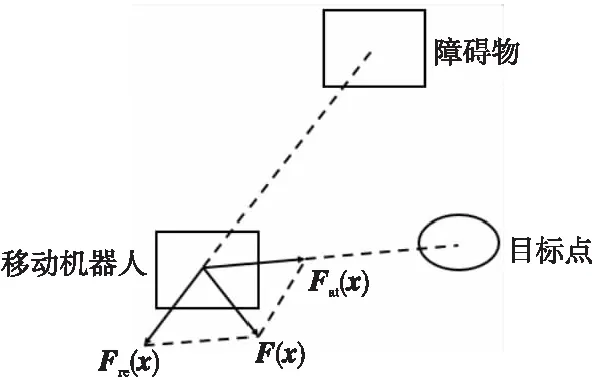
Figure 3 Schematic diagram of artificial potential field method

引力场的计算公式如式(3)所示：

(3)

其中,Kat为引力增益常数，Xg为目标点的位置向量。吸引力为引力场的负梯度，根据式(3)可得出：

Fat(X)=-Kat(X-Xg)

(4)

斥力场的计算公式如式(5)所示：

(5)

其中,Kre为斥力增益常数，pobs(X)=X-Xobs为移动机器人与障碍物的最短距离，Xobs为障碍物的位置向量，p0为单个障碍物最大影响距离。

斥力的计算公式如式(6)所示：

(6)

3.2 存在的主要问题

传统人工势场法存在的主要问题是局部极小点问题，其含义为移动机器人运动到某一点，其所受斥力等于引力，使得自身合力为零，从而导致移动机器人误以为已经达到目标点，停止运动[14]。具体局部极小点出现情况如图4所示，其中图4a表示当移动机器人移动时，障碍物和目标点在同一条线上，并且障碍物在机器人和目标点的中间。在这种情况下，斥力和引力大小相等，方向相反，导致作用在移动机器人上的合力为零，移动机器人停止移动。图4b为当目标点在障碍物的作用区域内时，障碍物的斥力将移动机器人推离目标点。当移动机器人遇到包含复杂形状障碍物的环境情况如U型障碍时，如图4c所示，机器人被困在该区域内。

Figure 4 Occurrence of local minima

4 基于模拟退火算法的人工势场法

4.1 基本原理

移动机器人在陷入局部极小点时，本文在原来所设定目标点附近位置添加随机目标点，通过在移动机器人上施加额外的力，打破原有的力平衡，从而使移动机器人在障碍物、目标点和随机目标点的共同作用下从局部极小点区域中逃脱，并继续向目标点移动。设置随机目标点受力如图5所示。

Figure 5 增设随机目标点受力分析

增设随机目标点后，受到的合力如式(7)所示：

F=Fat+Fre+Fr≠0

(7)

其中,Fr为增设随机目标点对移动机器人的引力。

4.2 增设随机目标点

本文设置随机目标点的原则是在移动机器人当前点关于障碍物取右对称点，距离为所设定一个步长值，如图6所示，增设的目标点的引力会引导机器人向着障碍物组外侧移动直至脱离其影响范围。

Figure 6 Adding random target point

模拟退火算法是一种基于蒙特卡洛的近似求最优解优化算法。算法运算过程中通常有2层循环，外部循环和内部循环，其中外部循环代表温度的连续下降，内部循环是在此温度下的多重干扰而产生的不同的态。内部循环是按Metropolis 准则接受新状态，粒子在温度T时趋于平衡的概率为exp(-ΔE/(kT))，其中E为温度T时的内能，ΔE为其改变数,k为Boltzmann常数[15]。Metropolis准则常表示如式(8)所示：

(8)

其中，Xn为后一时刻；Xo为前一时刻；E(Xn)为Xn时刻的内能；E(Xo)为Xo时刻的内能；T代表当前时刻温度。

模拟退火算法中温度T以一定的方式减小，如式(9)所示:

T(t)=αT(t-1)

(9)

其中,α为略小于1的正常数，其取值为0.85<α<1，t为迭代次数。

基于模拟退火算法的人工势场法逃离局部极小点区域的具体过程为，在当前处于局部极小点x处选择一个随机点x1,然后根据式(1)分别计算出点x与点x1处的势场U(x)和U(x1),如果满足U(x1)≤U(x),则接受点x1作为下一个点；如果满足U(x1)>U(x),则以概率p接受该点作为下一个点。基于模拟退火算法的人工势场法整体流程如图7所示。

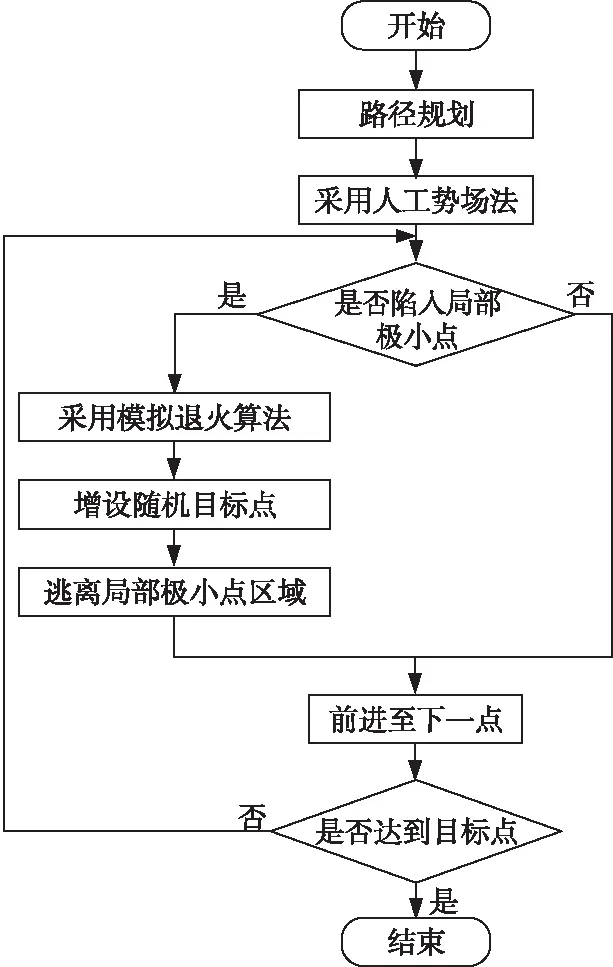
Figure 7 Whole process of artificial potential field method based on simulated annealing algorithm

4.3 具体步骤

本文方法具体流程图如8所示，其具体步骤如下所示：

步骤1判断是否陷入局部极小点，即判断移动机器人所受合力是否为0。若是则陷入局部极小点，否则无。

步骤2设置x=S(S为局部极小点)。

步骤3设置模拟退火算法温度初始值T0和终止值Tf。

步骤4根据随机目标点设置原则产生一个随机点x1=x+Δx(Δx为x一个步长)。

步骤5计算点x1处的势能U(x1)。

步骤6计算Δ=U(x1)-U(x)。

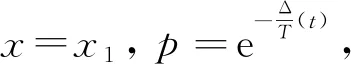
步骤8如果U(x1)≤U(S)，则成功逃离局部极小点区域。否则判断T≤Tf,如果成立则结束，代表本次逃离局部极小点失败；如果不成立，令T(t)=αT(t-1)，跳至步骤3，直至逃离局部极小点。

Figure 8 Flow chart of method in this paper

5 实验仿真结果

为了验证基于模拟退火算法的改进人工势场法路径规划的可行性，通过 Matlab R2018a分别对传统人工势场法和本文所设计的方法在局部极小点情况下的路径规划结果进行对比，初始参数设置如表1所示。

Table 1 Simulation initial parameter setting

首先，只利用传统人工势场法进行仿真。圆形表示为障碍物，虚线表示为障碍物的影响范围。黑色线段表示移动机器人的运动轨迹。本文主要针对2种情况进行仿真：第1种情况，当目标点距障碍物很近，移动机器人的起点坐标为(0,0)，终点坐标为(8,7)，仿真结果如图9所示。第2种情况，当环境中出现U型障碍物，移动机器人的起点坐标为(0,0)，终点坐标为(10,9)，仿真结果如图10所示。

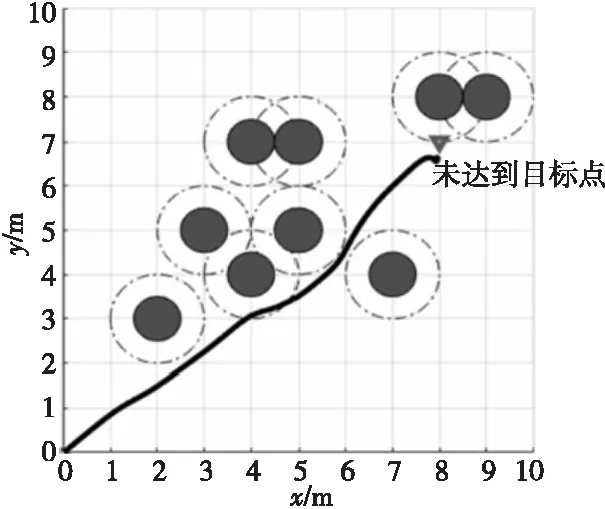
Figure 9 Not reaching the target point

Figure 10 U-shaped obstacle

从图9可以看出，当目标点靠近障碍物并且在障碍物的影响范围内时，移动机器人陷入局部极小点导致无法到达目标点。从图10可以看出，当环境中存在U形障碍物时，移动机器人无法从U形障碍物中逃脱。

利用本文所设计方法进行仿真实验。针对图9所示情况，目标点离障碍物很近，未能达到目标点，仿真结果如图11所示；在针对图10所示情况，出现U型障碍物，移动机器人未能逃离U型障碍物，仿真结果如图12所示。

通过对比可以看出，对于第1种情况，当目标点距障碍物很近时，本文所设计的方法能成功到达目标点，其中点状部分为模拟退火算法增设随机目标点过程；对于第2种情况，当环境中存在U形障碍物时，使用本文方法能成功避开U型障碍物，最终快速到达目标点。

Figure 11 Path planning of our method when not reaching the target point

Figure 12 Path planning of our method when U-shaped obstacle appeared

斥力增益常数Kre取值过大，会使移动机器人在运动过程路径产生震荡问题，因此将斥力增益常数Kre取值为30与取值为18这2种情况进行对比，如图13所示。通过对比可以看出Kre取值为30时，利用本文算法规划移动机器人运动路径并未出现震荡问题，但是路径长度有所增加。

Figure 13 Path planning with different Kre

本文选取文献[9]中改进势场函数方法与本文方法进行对比，实验参数设定如表2所示。图14所示为未达到目标点时对比情况(情况1)，图15为出现U型障碍物时对比情况(情况2)。

Table 2 Experimental parameters setting

Figure 14 Comparison of case 1

Figure 15 Comparison of case 2

本文方法和文献[9]方法在情况1与情况2时所用时间如表3和表4所示。

Table 3 Time comparison of case 1

Table 4 Time comparison of case 2

根据图14和图15、表3和表4可以看出，本文提出的基于模拟退火算法的人工势场法，所规划路径的平滑性优于文献[9]方法的，并且用时较短，能够成功让移动机器人到达目标点位置。

6 结束语

传统人工势场法容易在路径规划中陷入局部极小点，使得移动机器人无法运动到目标点。本文首先阐述了路径规划的整体思路，其次论述了传统人工势场法的基本原理，对传统人工势场法中存在局部极小点问题进行详细分析。针对此问题，本文提出一种基于模拟退火算法的人工势场法，利用模拟退火算法在当前局部极小点的位置附近，增设随机目标点，引导移动机器人逐渐逃出局部极小点区域。最后通过Matlab仿真表明，本文所设计的基于模拟退火算法的人工势场法能使得移动机器人逃离局部极小点位置，成功到达目标点位置，且用时较短。在后续的工作中，将考虑更多复杂环境且对移动机器人路径的最优性进行更进一步分析。