动态特征选择算法对恶意行为检测的优化研究*
2022-04-21王梓宇
刘 云,肖 添,王梓宇
(昆明理工大学信息工程与自动化学院,云南 昆明 650500)
1 引言
在线社交网络OSN(Online Social Net)拥有庞大的用户群,吸引来自不同行业和年龄段的用户。尽管大多数OSN主要用于各种良性用途,但其自身的开放性、庞大的用户群和消息实时扩散使OSN成为网络罪犯有利可图的目标。OSN已经被证明是一种新的具有复杂攻击和威胁的孵化器,例如网络欺凌、传播谣言、网络诈骗、发送垃圾邮件和其他非法活动[1]。如何自动分析用户行为特征以检测出在线社交网络中恶意用户行为,成为一项重要而具有挑战性的研究任务。
刘勘等人[2]提出基于随机森林分类的恶意用户检测算法,从多维度分析恶意用户的特征指标,构建对应的特征向量,并用随机森林算法设计恶意用户识别模型。Zhang等人[3]通过研究用户行为的各种区别属性和特征,提出一个动态的恶意用户行为检测框架,能自动处理不断变化的恶意用户行为。
Zadeh[4]提出的模糊集,引入了隶属函数和隶属度的思想,并由Ruspini[5]成功地将其应用于聚类中。在模糊聚类中,Dunn[6]提出的模糊C均值FCM(Fuzzy C-Means)算法是最著名的算法。模糊聚类在各种应用中被认为是一种非常强大的工具,已被广泛应用于各个领域,在基于用户行为特征的恶意用户行为检测中也卓有成效。Do等人[7]提出了基于模糊集的恶意用户检测SDAFS(Spammer Detection Algorithm based on Fuzzy Set)算法,通过使用网络方法检测恶意用户行为,然后利用FCM聚类算法找到用户所属聚类。Pinandito等人[8]提出基于模糊聚类的极限学习ELAFC(Extreme Learning Algorithm Based on Fuzzy Clustering)算法,通过分析用户个人资料、活动和相关文本等特征,采用具有特征加权的FCM聚类算法对用户行为进行聚类。Xu 等人[9]提出了一种基于网络方法检测恶意行为NADMB(Network-based Algorithm for Detecting Malicious Behavior)算法,该算法利用K-means聚类识别恶意群体。
但是,SDAFS算法由于使用模糊C均值聚类算法使得所有特征权重相同,影响了聚类精度。ELAFC算法虽然使用特征加权技术优化了在多维特征下的聚类精度,但没有考虑特征选择,冗余特征依然会影响系统性能。而NADMB算法由于使用的特征较少,导致算法只能应用于特定网络。
本文在已有研究工作的基础上,综合考虑以上算法的优缺点,提出一种动态特征选择算法DFSA(Dynamic Feature Selection Algorithm)。该算法使用具有特征加权熵的模糊C均值目标函数,为参数构建一个学习模式,通过多次迭代计算得出每个特征权重,剔除不相关或冗余的特征,对特征进行动态选择,迭代地更新隶属函数、簇中心和特征权重直到最优化为止,最终识别出具有高精度的恶意簇。仿真结果表明,对比SDAFS算法、ELAFC算法和NADMB算法,本文提出的DFSA算法在Rand指数[10]、Jaccard指数[10]和归一化互信息量3个主要性能指标上均有改善。
2 聚类模型
2.1 模糊C均值聚类框架
图1所示是典型的模糊C均值聚类框架图,由特征提取、模糊C均值聚类算法和标记3部分组成。首先,使用特征提取器从数据集中提取特征,每个特征被数字化后由一个特征向量表示。然后,通过使用模糊C均值聚类算法对新的数据集进行聚类,得出预先设定好的簇数,对模糊簇进行标记得出最终结果。
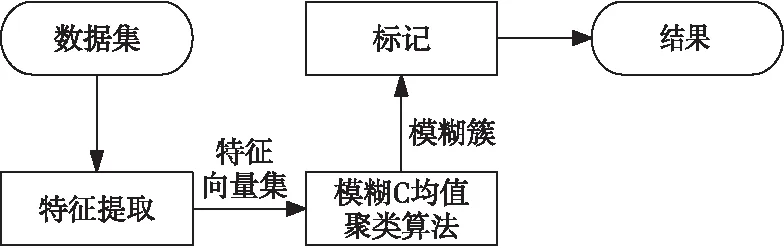
Figure 1 Framework of fuzzy C-means clustering
在恶意用户行为自动检测方法中,可将定义特征的数据集类型分为基于元数据的特征、基于内容的特征和基于社区交互的特征[3]。由于复杂的恶意用户行为可以通过使用随机数生成器算法轻松地避免基于元数据的特征,因此基于元数据的特征的区分效率较低,DFSA算法将对基于内容和基于社区交互的特征进行特征提取。现有自动检测恶意用户行为相关文献中对多个具有识别能力的特征有明确的定义,其中包括唯一URL比率 (F1)[11]、唯一提及率(F2)[11]、标签比例(F3)[12]、提及率(F4)[11]、URL比率(F5)[13]、声誉(F6)[11]、粉丝数比率(F7)[12]和聚类系数(F8)[13],在此基础上本文又定义了4个基于社区交互的新特征,包含粉丝声誉比(F9)、粉丝关注比(F10)、社区声誉(F11)和社区聚类系数(F12)。下面详细解释这4个新特征:
(1)粉丝声誉比(F9):用户的声誉通常不是他们自己的,而是从追随他们的粉丝那里继承的。通常用户无法控制其粉丝,并且难以逃避和篡改基于粉丝的特征。用户的声誉与其粉丝的声誉成正比,此特征反映了用户粉丝的声誉。用户u的粉丝的声誉为粉丝的声誉总量与粉丝总量之比。
(2)粉丝关注比(F10):恶意用户对每个请求都非常敏感,无论发件人的身份如何,他们都只是为了增加其关注者列表,而良性用户则在响应未知用户的请求时会有意识地筛选。因此,为检测用户粉丝的连接行为,可根据用户的粉丝模式来分析粉丝的关注者模式。用户u的粉丝关注比为粉丝关注数的平均值与粉丝数之比。
(3)社区声誉(F11):用户的声誉取决于与用户相关联的社区及其成员的声誉。为了计算用户u的F11值,首先从u的附近网络中找到社区;然后,计算每个社区的每个用户的声誉;最终根据其成员的声誉来计算每个社区的声誉和。
(4)社区聚类系数(F12):此特征研究用户社区成员之间的连接密度。用户u的社区聚类系数为用户所在的所有社区聚类系数的均值。
对用户特征提取和数字化后,数据集中每个用户可用如式(1)所示的特征向量来表示:
ui=〈F1,F2,…,F12〉
(1)
根据用户的关注者和粉丝之间的联系来考虑社区交互,本文使用一种快速社区检测算法[14]来识别用户交互网络中的社区。图2展示了一个用户交互网络的案例,图2b为用户A所连接的用户及其与其他用户连接形成的社区,其中C1和C2表示可能存在的社区结构。对于恶意用户来说,由于粉丝和关注者的随机性,交互网络中的用户几乎相互不认识,从而导致形成的社区非常稀疏或没有社区。因此,可以通过分析社区成员来分析用户行为。

Figure 2 User interaction network
2.2 模糊C均值聚类算法
算法中使用的大多数符号总结如表1所示。

Table 1 Symbol list
令X={x1,…,xn}是d维空间中的数据集,FCM目标函数定义如式(2)所示:
(2)
使其服从
其中μik∈[0,1],1≤i≤n,1≤k≤c。
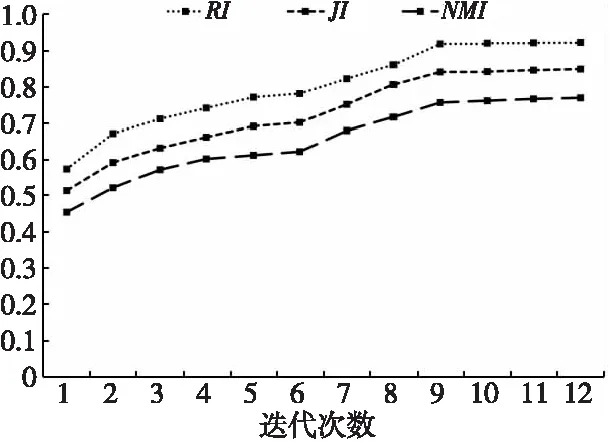
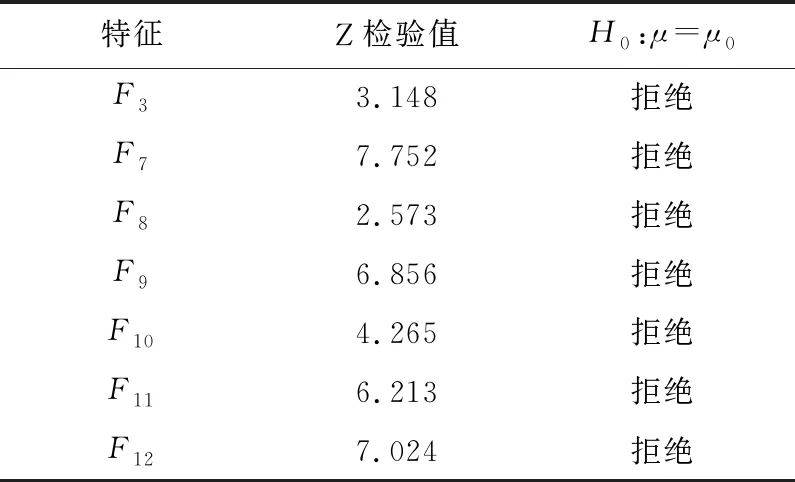
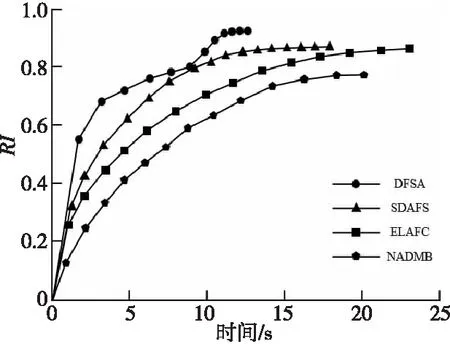
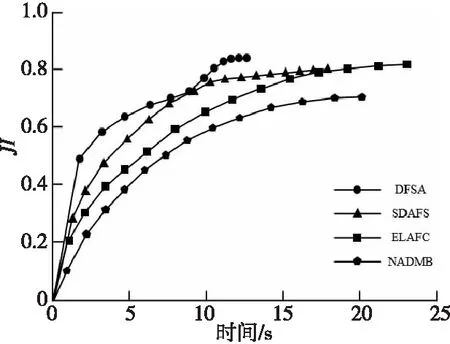
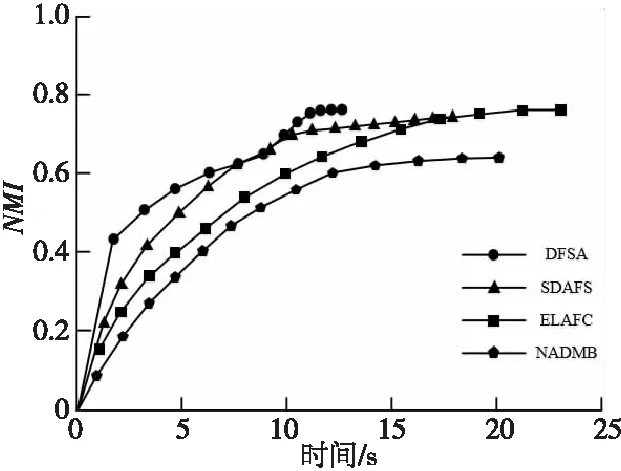
加权指数1 (3) (4) 且满足1≤i≤n。 FCM中所有的特征无论是否相关,其权重大小都是相等的,所以容易导致聚类结果不正确,其缺陷可通过例1来解释。 Figure 3 Clustering results 最后将2个簇分别标记为恶意簇和良性簇。考虑已知的用户行为特征分布情况[ 12,13],将对不同用户行为区分度较大的特征F3和F7再次使用在此任务中。将以上特征平均值高的簇标记为良性簇,另一个簇相应地被标记为恶意簇。 图4所示是动态特征选择算法框架图,由特征提取、DFSA算法和标记3部分组成。首先,使用特征提取器从用户数据集中提取12个特征,每个用户特征被数字化后由一个特征向量表示;然后,使用动态特征选择算法对用户特征向量数据集进行聚类;最终得出2个簇,并分别标记为良性簇和恶意簇。 Figure 4 Framework of DFSA algorithm 由于数据集可能包含一些冗余或不相关的特征,因此特征选择在聚类算法中非常重要。本文提出了一种动态特征选择算法,利用特征加权熵进行特征选择,以改进模糊C均值聚类算法。在此算法中,每个特性都有自己的权重,这些权重将在每次迭代时更新,并剔除权重小于阈值的特征,动态选择重要的特征分量。令X={x1,…,xn}为d维空间中的数据集,DFSA目标函数如式(5)所示: (5) 使其服从 (6) 其中δj控制特征权重。 DFSA算法通过3个最小化步骤来求解。 (7) 对式(7)的μik求拉格朗日偏导数并使其值为0,可得出式(8): (8) 从更新的式(8),可求得μik如式(9)所示: (9) (10) 由式(10)可得vkj的更新如式(11)所示: (11) (12) 由式(12)可得ωj的更新如式(13)所示: (13) (14) 其中,dnew表示更新后得到的特征成员数。 衡量离散度的一个著名指标是方差-均值比(VMR),其定义为VMR=σ2/μ,用于观察离散或聚集的数据集。离散度越小,表示数据集离簇中心越近;离散度越大,表示数据集离簇中心越远。由于需要保留离散度小的特征,抛弃离散度大的特征,因此考虑VMR的倒数,即均值-方差比(MVR)[16]。 将MVR应用在本文算法中,因为在DFSA算法中特征j的(mean(x)/var(x))j可以表示数据集中簇之间的离散度。因此,使用(mean(x)/var(x))j作为δj的值,如式(15)所示: (15) DFSA算法流程如算法1所示: 算法1DFSA算法 输入:固定ε>0,取簇数c=2,初始化簇中心V(0),初始化特征权重W(0),W(0)=[ωj]1×d,X={x1,…,xn},j=1,…,d,ωj=1/d,且令t=0。 输出:最佳聚类结果C*。 1:输入数据集X,通过式(15)计算出δj; 2:输入δj,V(t-1)和W(t-1),通过式(9)计算出隶属函数U(t); 3:输入U(t),通过式(11)更新簇中心V(t); 4:输入δj,U(t)和V(t),通过式(13)更新W(t); 5:forj≤ddo 6:dr=0; 8: 丢弃特征权重小于阈值的特征ωj; 9: 且设dr=dr+1; 10:end 11:end 12: 设共丢弃dr个特征,dnew=d-dr; 13: 根据式(14)调整W(t); 14:if|‖W(t)‖-‖W(t-1)‖|<εthenstop 15: 得出最佳聚类结果C*; 16:else 17: 令t=t+1,dnew=d返回第1步; DFSA算法首先固定ε和c的值,初始化簇中心V(0)和特征权重W(0),进入第1次迭代计算,分别得出更新后的δj,U(t),V(t)和W(t)。然后判断并丢弃权重小于阈值的特征,调整特征成员数得出新的W(t)值。最终判断聚类结果是否达到最优,若达到则退出循环并输出最佳聚类结果C*,否则开始新的一次迭代计算过程。 为进一步研究算法的计算复杂度,可将DFSA算法分为3个部分: (1)计算模糊隶属度(μik)划分需要O(nc2d); (2)更新簇中心(vk)需要O(nc); (3)更新特征权重wj需要O(ncd2)。 符号O(·)仅考虑函数增长率的上限,则DFSA算法的总计算复杂度为O(nc2d+ncd2),其中n为数据点的个数,c为簇数,d为数据点维数。 为测量聚类性能,本文选用Rand指数、Jaccard指数和归一化互信息NMI(Normalized Mutual Information)作为评价指标,其定义如下所示: 设C是数据集中的原始簇,C*是通过聚类算法得到的簇集合。对于一对点(xi,xj),E表示2个点在C和C*中属于相同簇的对数;F表示2个点在C中属于相同簇,而在C*中属于不同簇的对数;G表示2个点在C中属于不同簇,而在C*中属于相同簇的对数;L表示2个点在C和C*中都属于不同簇的对数。 (1)Rand指数RI(Rand Index)如式(16)所示: (16) (2)Jaccard指数JI(Jaccard Index)如式(17)所示: (17) (3)归一化互信息(NMI)如式(18)所示: (18) 其中,H(X)是X的熵,I(X:Y)是H(X)和H(Y)之间的互信息量。 与类似论文一致,为了验证DFSA算法的有效性,本文选取通用数据集,即从微博的登录服务器上收集到的真实登录事件的数据集[17]。该数据集中有11 000个带有标签的用户,包含10 000个良性用户和1 000个恶意用户;还包含带有标签用户的关注者和粉丝列表及其用户文件信息,如用户名、位置和用户ID;还包含微博和相关的详细信息,如微博ID、创建时间和已标记用户的收藏计数等。 表2列出了数据集的简要统计信息,其中用户总和包括标记为良性用户和恶意用户的所有关注者和粉丝。在这个数据集中,大多数良性用户没有他们的粉丝者列表,因此他们基于社区交互的特征值为零,这将会导致算法在检测时有所偏差。若只考虑有粉丝者列表的实例(218个良性用户和1 000个恶意用户),就会导致数据不平衡问题。为了解决该问题,本文使用合成少数过采样技术SMOTE(Synthetic Minority Oversampling Technique)[18],以生成与数据集少数类相关的合成样本。针对SMOTE中的样本数据点,将识别其相邻数据,并根据样本点及其相邻数据之间的差异生成合成样本。通过SMOTE生成了782个良性类的实例来平衡数据集。在公有云平台上使用具有2 GHz 64位QEMU(Quick EMUlator)虚拟CPU的虚拟主机,并使用Networkx Python Library提取连接的组件。 Table 2 Data set statistics DFSA算法首先更新集群中心和成员矩阵,然后计算新的特征权值,并在聚类过程中丢弃权值较小的特征。选择出高度关联的特征后调整数据点和聚类中心,将新的特征权重、聚类中心和隶属度矩阵代入算法第1步重新开始计算,迭代过程一直持续到目标函数最小化为止。 图5显示了DFSA算法迭代次数对应的目标函数值和迭代时间,目标函数总共经过12次迭代后收敛。经过6次迭代后部分特征被丢弃,从那时起目标函数收敛速度明显加快。同时,后几次迭代的计算时间比前几次迭代需要的时间更少。从第9次开始,迭代所需的时间比第1次迭代减少了75%以上。这意味着经过前几次迭代后,由于部分不重要的特征被丢弃,使得计算时间会迅速减少。 Figure 5 DFSA objective function convergence and iteration time 图6所示是DFSA算法每次迭代对应RI、JI和NMI的变化情况。随着迭代次数的增加,3个聚类性能指标均在提高,且第9次迭代后的聚类性能相比第6次有明显提高。 Figure 6 DFSA iterative calculation time 12个特征最初具有相同的权重,经过6次迭代之后F1、F2、F4、F5和F65个特征权重低于阈值,在聚类过程中被丢弃,算法最终保留了其余7个重要的特征。特征权重的变化也说明算法通过多次迭代后,因为特征减少明显加快了后几次迭代计算的速度。 通过统计显著性分析来验证算法所保留特征在用户间的差异是否是随机的,为了验证这个假设,对4.1节讨论的微博数据集[16]进行双边Z检验。在Z检验中,原假设下检验统计量服从正态分布,采用2种假设进行评估,即原假设(H0:μ=μ0)和备择假设(H1:μ≠μ0)。 在原假设中,假设恶意用户和良性用户之间定义的特征值的总体均值没有显著差异,而在备择假设中,假设2种不同用户特征值的均值存在显著差异。计算被算法保留的7个特征检验统计量,并与表3中在5%显著性水平下的双边Z统计量临界值(±1.96)进行比较。分析中发现,7个特征均拒绝原假设,如表3所示,因此可以看出恶意用户和良性用户的这7个特征均值存在显著差异。且从表3中可以看出,恶意用户和良性用户之间F7和F12的平均值差异最大。根据Zhang等人[3]对用户行为特征累计分布的统计及以上的显著性分析可以推断,DFSA算法所选择的特征对于分离不同用户行为是重要的。 Table 3 Z-test statistics for selected features 将本文所提出的DFSA算法与SDAFS算法、ELAFC算法和NADMB算法进行对比实验,分别得出4种算法在不同迭代时间下的Rand指数(RI)、Jaccard指数(JI)和归一化互信息(NMI)。 如图7所示,4种算法的RI都随着迭代次数的增加逐渐提高,直到最终收敛到最高值为止。DFSA算法的RI最高且收敛速度最快,SDAFS算法与ELAFC算法的RI相近,但ELAFC算法收敛速度更慢,而MADMB算法的RI最低且收敛速度也较慢。 Figure 7 RI changes with time of different algorithms 如图8所示,DFSA算法的JI最高,ELAFC算法的JI次之,SDAFS算法的JI较低,而NADMB算法的JI最低。 Figure 8 JI changes with time of different algorithms 如图9所示,仿真结果对比显示DFSA算法的NMI值最高,ELAFC算法的NMI值次之,SDAFS算法的NMI值较低,NADMB算法的NMI值最低。 Figure 9 NMI changes with time of different algorithms 通过分析3个主要性能指标随时间变化情况可知,本文所提的DFSA算法相比SDAFS算法、ELAFC算法和NADMB算法的聚类性能更好,且迭代次数更少,收敛速度明显更快。结合特征权重变化,DFSA算法剔除了冗余或不相关的特征,输出了与用户行为高度相关联的簇。SDAFS算法和NADMB算法不涉及特征选择,虽然具有较快的收敛速度,但冗余特征影响了聚类性能。而ELAFC算法计算了特征权重,一定程度上使聚类性能有所提升,但也导致了计算复杂度的增加,收敛速度变慢。 为了发现在线社交网络中进行复杂恶意活动的恶意用户簇,本文提出一种动态特征选择算法(DFSA)。不同于大多数的特征加权算法,该算法将动态特征选择模式嵌入到聚类过程中,在第1次迭代中所有的特征都会被使用,然后在每次迭代中更新特征权值,并用阈值剔除权值较小的特征,后续步骤中使用的特征数量将逐渐减少,动态选择出重要的特征分量,迭代地更新隶属函数、集群中心和特征权重,直到优化为止,最终识别出具有高聚类精度的恶意用户簇。仿真结果表明,对比SDAFS算法、ELAFC算法和NADMB算法,DFSA算法在Rand指数(RI)、Jaccard指数(JI)和归一化互信息量(NMI)3个主要性能指标上均有改善。DFSA算法相比传统算法的优势在于能动态选择重要的特征,不仅提高了收敛速度,而且通过剔除不相关的特征降低了特征维数,提高了聚类精度。在未来的工作中,将考虑使用多个社交网络用户数据集进行更多测试,包括检测算法在不同特征和不同数据集大小情况下的聚类性能,以及算法的鲁棒性。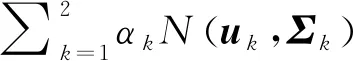

2.3 模糊簇标记
3 DFSA算法
3.1 DFSA算法介绍
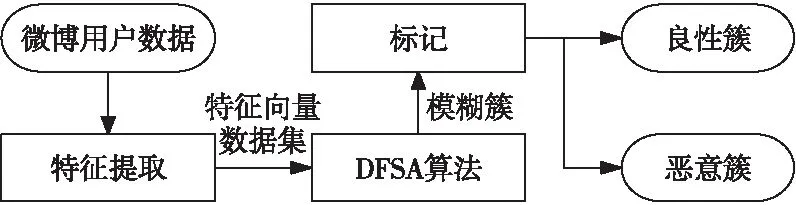
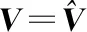
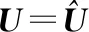
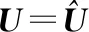
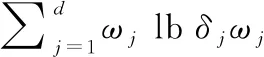

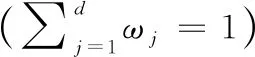
3.2 算法流程
3.3 算法复杂度分析与评价指标
4 仿真分析
4.1 数据集及仿真环境

4.2 算法目标函数与收敛性分析

4.3 聚类精度及特征显著性分析
4.4 算法聚类性能对比分析
5 结束语
