基于特征结构不变性思想的自适应在线神经网络算法

2022-04-21姜海富于化龙

江苏科技大学学报(自然科学版) 2022年1期

韦磊, 姜海富, 于化龙,2*

(1.江苏科技大学计算机学院, 镇江 212100)(2.四川轻化工大学人工智能四川省重点实验室, 宜宾 643000)

在线学习(online learning)，又称数据流学习(learning from data stream)，是机器学习领域的重要研究分支之一[1].所谓在线学习，是指数据的获取不是一次性的，而是随着时间不断动态累加的.当前，随着移动互联网与物联网等技术的高速发展，在线学习在智能交通[2]、市场分析[3]、网络安全[4]，乃至更多的应用领域都存在着广泛的应用价值.

相比于传统的依赖于静态数据的机器学习，在线学习通常要面临更多的挑战，主要包括：① 考虑到数据流高频、量大的特点，以及存储的限制，通常数据都是在使用后即被抛弃的，因此要求模型只能访问数据一次(one pass)；② 数据的分布可能会随着时间的延展而发生各种动态改变，即概念漂移(concept drift)问题[5]，因此要求模型要能实时跟踪分布的变化而不断实现自我进化.

对于one pass 问题，现有的解决策略大体可以分为两类：一是对传统的单一静态学习模型进行改进，令其可适应在线学习环境，当接收到新数据时，通过自动修正模型参数使其同时适应新旧两类数据[6-7]；二是将传统的单一静态学习模型与集成学习框架相结合，不同的个体学习器建立于不同的数据块之上，通过投票规则相关联，同时兼顾新旧经验[8-10].对于概念漂移问题，通常采用一个独立的分布漂移检测模块来对漂移的发生进行监测，进而将监测的结果反馈给单一学习模型以调控其对旧经验的遗忘[5,11-12]，或集成学习模型以分配不同个体学习器的决策权重.上述策略尽管有效，但如何设计合理的遗忘函数及决策权重分配函数却是一个困难的问题，其很可能直接影响到最终的学习效果.

文中从一个全新的角度来考虑在线学习模型对概念漂移的自适应问题，即，模型能否不通过对分布漂移的检测与量化来适应概念漂移.文献[13]研究发现：大部分所谓的概念漂移实质上只是分布的值域随时间而发生了变化，而其内在的概念结构却并未改变，因此采用增量离散化的方法来追踪特征的值域变化，从而实现了对特征结构的动态保持，有效解决了概念漂移的问题.但增量离散化也存在一个问题，即采用离散化属性值来取代连续型属性值，很可能会造成信息损失，进而影响到学习的效果.

基于特征结构不变性思想，文中提出了一种概念漂移自适应在线神经网络算法，首先采用增量离散化技术来适应概念漂移，并保持特征结构，然后利用增量聚类技术来挖掘并细化特征的内在结构，进而采用一种类似深度森林算法[14]中的特征构造策略在特征内在结构上提取连续型的辅助结构特征，最后将这些辅助特征与原始特征相结合，扩充数据的特征空间，用来训练并更新在线神经网络模型.显然，辅助特征既体现了原始特征的潜在内部结构，对分布漂移不敏感，同时又体现了样本在原始特征潜在内部结构中的细微差异性，从而为学习提供了更为丰富的信息.此外，考虑到在线学习所普遍具有的实时性需求，采用在线序列极限学习机算法(online sequential extreme learning machine，OS-ELM)[15]作为在线神经网络的训练算法，该算法同时兼具训练速度快与鲁棒性高的特点.通过8个基准的在线数据集验证文中算法的有效性、可行性和优越性进行了验证，结果表明：文中算法不但对概念漂移可以自适应，而且相比于传统的概念漂移自适应策略，要具有更好的性能.

1 研究方法

1.1 增量离散化

离散化(discretization)是数据挖掘领域中一种常用的技术，用于将连续型的属性转化为离散型属性[16].离散化技术采用设置断点的方式将连续的属性取值区间转化为若干的容器(bin)，每一个容器对应于一段连续取值区间，取值于某一区间的属性值则用对应容器的离散值来取代.

文献[13]提出了两种增量的离散化算法，分别命名为Ida和Idaw，在动态数据流中，前者可保持近似的等频分布，而后者则可保持完整的等频分布.采用增量离散化能有效追踪数据分布的变化，并很好地保留特征结构中潜在概念，适合解决概念漂移问题，但由于将连续属性转化为离散属性，也将会导致大量的有效信息损失，进而影响到最终的学习效果.

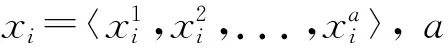
在IDA和IDAW算法中，均采用等频方式来实现属性的离散化，即保证在每一个容器内的样例数近似相等.初始的样本集记做V，首先对其等频离散化，得到断点序列〈κ1,κ2,...,κm-1〉，然后，在增量的过程中，使用新接收到的样例来取代V中的旧样例，并对断点序列进行更新，实现增量离散化.上述过程中，IDA和IDAW算法之间的不同之处在于：前者在新接收样例中随机选择个体进行断点序列的更新，且用新样例随机取代V中的样例，而后者则采用每一个新接收的样例来更新断点序列，且新样例取代V中最旧的样例.因此，相比于IDA算法，IDAW算法对数据分布的跟踪要更及时，但时间复杂度也要更高.

IDA和IDAW算法的流程简单描述如下：

算法1 s: m: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18.IDA算法thevolumeoftheuser-definedrandominstancesetthenumberoftheuser-definedbinsprocedureD=IDA(S={x1,...,xn},s,m) collecttheinitialsinstancesasV fori=1toado Qi=INITIALDISCRETIZATION(Vi,m) endfor fori=1tosdo Di=DETECTDISCRETIZATION(xi,Q,m) endfor fori=s+1tondo ifrand()≤s/ithen V=UPDATESAMPLES(xi,V) forj=1toado (Dji,Qj)=INSERTVALUE(V,m,Qj) endfor else Di=DETECTDISCRETIZATION(xi,Q,m) endif endforendprocedure

算法2 s: m: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15.IDAW算法thevolumeoftheuser-definedrandominstancesetthenumberoftheuser-definedbinsprocedureD=IDAW(S={x1,...,xn},s,m) collecttheinitialsinstancesasV putVintoabufferBbasedontheorderofreceiving fori=1toado Qi=InitialDiscretization(Vi,m) endfor fori=1tosdo Di=DetectDiscretization(xi,Q,m) endfor fori=s+1tondo (V,B)=UpdateSamples(xi,V,B) forj=1toado (Dji,Qj)=InsertValue(V,m,Qj) endfor endforendprocedure

其中，InitialDiscretization函数用于搜寻初始断点，划分容器；DetectDiscretization函数用于将原始的连续型属性值转化为对应的离散化值；UpdateSamples函数负责新样例对保留样例集V的更新；而InsertValue函数用于更新断点序列，并完成对新样例的离散化.

1.2 增量聚类

聚类技术是机器学习与数据挖掘领域的重要组成部分之一，有助于发现数据潜在的内在结构[17].其中K-means[18]最为经典.

在一个给定的数据集S={x1,x2,...,xi,...,xn}上，其中，xi∈Ra，采用K-means算法就是要根据样本在特征空间中的距离关系将S中所有样本划分入k个类簇c1,c2,...,ck，并最小化优化函数Z：

(1)

式中：ω1,ω2,...,ωk为各类簇的质心.

文中采用文献[19]中提出的序列K-means(sequentialK-means)算法来实现流数据的增量聚类，序列K-means算法每次对一个样本进行更新，即当接收到一个新样本xi时，采用下式来调整与其最近的聚类cj的质心：

(2)

式中：n为类簇cj中原有的样本数.

文中提出的IncrementalKmeans算法的流程描述如下：

算法3 s: k: 1. 2. 3. 4. 5. 6. 7. 8.IncrementalKmeans算法theuser-definedinitialnumberoflabeledinstancestheuser-definednumberofclustersprocedurec=IncrementalKmeans(S={x1,...,xn},s,k) collecttheinitialsinstancesasS0 [cl1～cls,ω1～ωk,P1～Pk]=InitialKmeans(S0,k) fori=s+1tondo findωjwhichisthenearestclustercentertoxi tuneωjwithPjandxiaccordingtoEq.(2) letcli=j endforendprocedure

其中，InitialKmeans函数在初始的S个样本上执行聚类，并为其分配类簇标记cl1～cls，生成各类簇质心ω1～ωk，以及统计各类簇中初始的样本数P1～Pk.在在线学习过程中，新接收的样例将会不断更新ω和P的取值.考虑到IncrementalKmeans算法运行于IDA或IDAW算法所构造的离散特征空间之上，故特征空间的稳定性可以得到有效保障，这也将有助于搜寻到数据真实的潜在内部结构.

1.3 结构特征抽取

在发现数据潜在内部结构的基础上，对结构进行描述，并进一步生成可量化的结构特征两方面入手：一方面提取能反应数据内部结构的全局描述特征，另一方面则充分利用聚类信息提取局部描述特征.

(3)

新的特征序列指明了样本在整体特征空间中的相对位置.

参照深度森林算法的思想，给出了一个结构特征抽取的示意图，如图1.假定真实类别数q与聚类数k均为3，则c1,c2,c3分别表示3个类簇，而g1,g2,g3表示样本到3个类簇质心的距离.从图1可以看出，在添加结构特征后，特征空间得到了有效扩充，维度从a转化为a+q+k，其中a与q是确定的，而聚类数k则是人为指定的.在实际应用中，可以通过仔细调控变量k，来保证对样本的最优描述.

图1 结构特征抽取过程

1.4 在线序列极限学习机

样本在经过维度扩增后，需要输入分类器进行学习和训练.文中采用单隐层前馈神经网络(single-hidden-layer feedback neural networks，SLFNs)作为分类模型，其优点在于可以以任意精度近似任意的非线性函数.图2为SLFNs的结构.

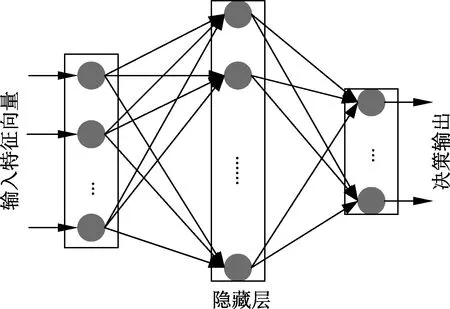
图2 单隐层前馈神经网络结构

对于SLFNs，已有多种成熟的学习算法，如误差反传(back-propagation,BP)算法[21]，但该算法需要通过迭代的方式来完成网络训练，因此，提出时间复杂度较高，极限学习机算法(extreme learning machine，ELM)算法来快速地训练SLFNs[22-23].相比于BP算法，ELM算法不但训练速度快，而且鲁棒性也通常更好[24].

假设对于一个具有n个训练样本的q分类问题，第i个样本表示为(xi,ti)，其中xi对应于一个a×1的输入向量，而ti对应于一个q×1的输出向量，若SLFNs中有L个隐层节点，且输入层与隐藏层间的权重和偏置均随机生成，则样本xi在隐藏层的对应输出可以描述为h(xi)=[h1(xi), }),...,hL(xi)]，ELM的数学模型可表示为：

Hβ=T

(4)

式中：H=[h(x1),h(x2),...,h(xn)]T为所有训练样本在隐藏层的输出；β为隐藏层与输出层间的连接权重；T=[t1,t2,...,tn]为全部训练样本的期望输出.显然，在上式中，只有β未知，故可通过最小二乘法对其进行求解，结果如下：

(5)

式中：H†为隐藏层输出矩阵H的Moore-Penrose广义逆，这可以保证所求得的解为公式(4)中方程的最小范数最小二乘解，进而保证模型的泛化性能.

对于在线学习，文献[15]基于ELM提出了一种在线序列极限学习机OS-ELM算法，该算法采用递归最小二乘策略拟合新接收的数据.通过大量理论推导，得出输出权重矩阵的更新规则为：

(6)

式中：Hi+1和Ti+1分别为所收到的第i+1个样本所对应的隐层输出和期望输出；而β(i)和β(i+1)则分别为更新前后的输出权重.Pi+1为：

(7)

表明Pi也是可以通过迭代的方式进行更新的，其初始值P0为：

(8)

式中：H0为最初的隐藏层输出矩阵.显然，无论Hi+1,Ti+1，还是Pi+1，均可用新接收的样本来进行计算和更新，故可保证β同时拟合新旧两类样本，而无需重新训练.因此，文中采用OS-ELM算法来训练在线神经网络模型.

1.5 文中算法

文中算法整合了增量离散化、增量聚类、结构特征抽取及在线序列极限学习机等技术，实现了在线学习对概念漂移的自适应.其中，增量离散化和增量聚类用于跟踪特征空间的变化，结构特征抽取用于适应概念漂移，在线序列极限学习机用于实现学习模型的动态更新.

文中提出的IncreFull算法流程描述如下：

算法4 s: m: k: L: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19.IncreFull算法theuser-definedinitialnumberoflabeledinstancestheuser-definednumberofbinstheuser-definednumberofclusterstheuser-definednumberofhiddennodesinELMprocedureΘ=IncreFull(S={x1,...,xn},s,m,k,L) collecttheinitialsinstancesasVandlabelthemast1～tsmanually Q=InitialDiscretization(V,m) D=DetectDiscretization(x1～xs,Q,m) [cl,ω,P]=InitialKmeans(D,k) [g1～gs,l1～ls]=NewFeatureExtraction(cl,ω,P) integrateg1～gsandl1～lswithx1～xstoformthenewfeaturevectorf1～fsβ=InitialElm(f1～fs,t1～ts,L) fori=s+1tondo updateQandVwithIDAorIDAW Di=DetectDiscretization(xi,Q,m) [cli,ω,P]=IncrementalKmeans(Di,ω,P) [gi,li]=NewFeatureExtraction(cli,ω,P) integrategiandlitoformthenewfeaturevectorfi Θi-s=Elm(fi,β) collecttherealclasslabeltifortheinstancexi β=OsElm(fi,ti,β) endforendprocedure

其中，NewFeatureExtraction函数用于抽取结构特征，InitialElm、Elm及OsElm函数则分别用于训练初始的学习模型，对新接收的数据进行预测及在接收到新数据时，对学习模型进行更新，而Θ则用于存储样本的预测类标，可通过与真实类标序列t的比较，计算出分类的精度.

2 实验结果与讨论

2.1 数据集

采用8个数据集验证所提算法的有效性、可行性与优越性.其中，Powersupply和HyperPlane数据集获取自Data Mining Repository；electricity来源于MOA网站；noaa数据集获取自美国国家环境信息中心，而其它4个，即SEA, spiral, Gaussian 和checkerboard，均为人工数据集，由对应的数据流生成器直接生成得到.这些数据集都或多或少地含有概念漂移，漂移类型与漂移量有所不同[25].表1给出了这些数据集的数据属性描述.

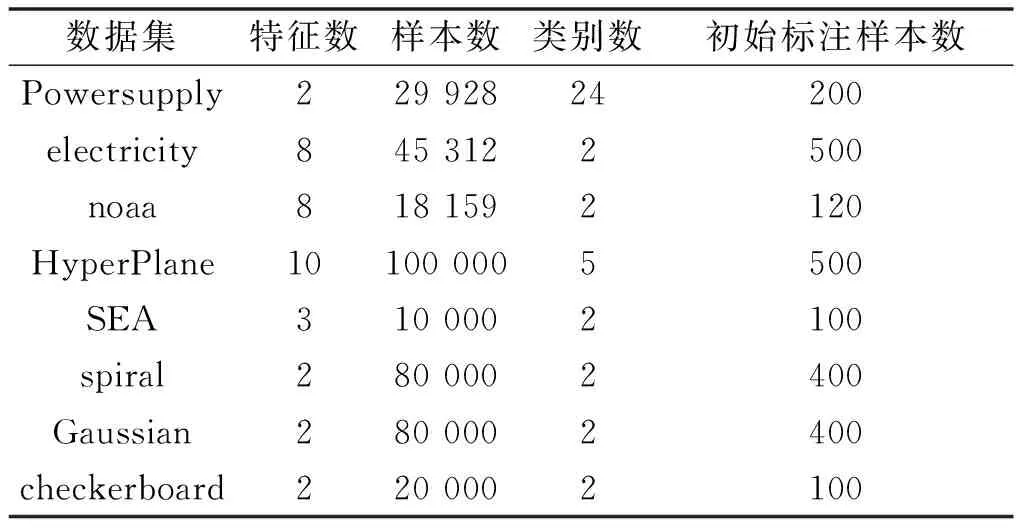
表1 数据集描述

2.2 实验设置

实验采用IDA和IDAW策略，并将算法简写为IncreFull-IDA和IncreFull-IDAW.同时，与以下几类算法进行了比较：

(1)IncreOnly: 该算法没有增量离散化，增量聚类和结构特征的提取过程，而只是采用数据原始特征结合OS-ELM算法来进行建模.

(2)IncreForg: 该算法不执行增量离散化，增量聚类和结构特征的提取过程，而是在OS-ELM模型上添加遗忘因子，遗忘系数采用缺省值0.01，即每一次更新，遗忘1%的旧经验[11].

(3)IncreDisc: 利用增量离散化技术生成离散特征，并用其取代原始的连续型特征，利用OS-ELM算法建模.

(4)IncreExtra: 该算法不执行增量离散化，而直接在原始的连续特征空间上直接进行增量聚类和结构特征抽取，并对原始特征空间进行扩增，最后通过OS-ELM算法进行建模.

(5)IncreMix: 利用增量离散化技术生成离散特征，并与原始的连续型特征进行整合，利用OS-ELM算法建模.

显然，可以将IncreOnly算法视为基线算法，IncreForg算法用于检测遗忘机制是否能真的适应概念漂移，同时与文中算法在概念漂移的适应性方面进行比较，IncreDisc与IncreMix算法用于验证采用离散化的特征是否会造成信息损失，对最终结果的影响又会是多大；IncreExtra算法用于验证增量离散化的作用，观察其是否适应概念漂移.关于各种算法分别采用了哪些功能模块，以及它们之间的具体区别，请参照表2.

表2 各种算法对不同功能模块的使用情况，√ 和 ×分别表示算法中包含/不包含对应功能模块

文中实验环境：Intel i7 6700HQ 8核CPU，每个核的主频为2.60 GHz，内存为16 G，代码运行环境为Matlab 2013a.

为了保证实验比较的公正性，所有的数据都做了标准化处理，即每个特征均等比例缩放到[0,1]区间.至于各比较算法中的共有参数，也根据经验对其进行了统一的设置，其中，离散化区间数m设为10，聚类数k设为5，ELM中隐藏层节点个数L设置为50.表1中所给出的初始标注样本数为初始模型建模的训练集，其它样本按照在数据集中的顺序逐一接收.此外，考虑到极限学习机作为在线学习器，其本身的随机性，每个实验均随机重复执行50次，并以均值±标准差的形式给出最终的结果.

2.3 结果分析

表3给出了各种比较算法的实验结果，评价指标为分类精度，其中，在每个数据集上，表现最好的算法所对应的实验结果已经做了加粗处理.

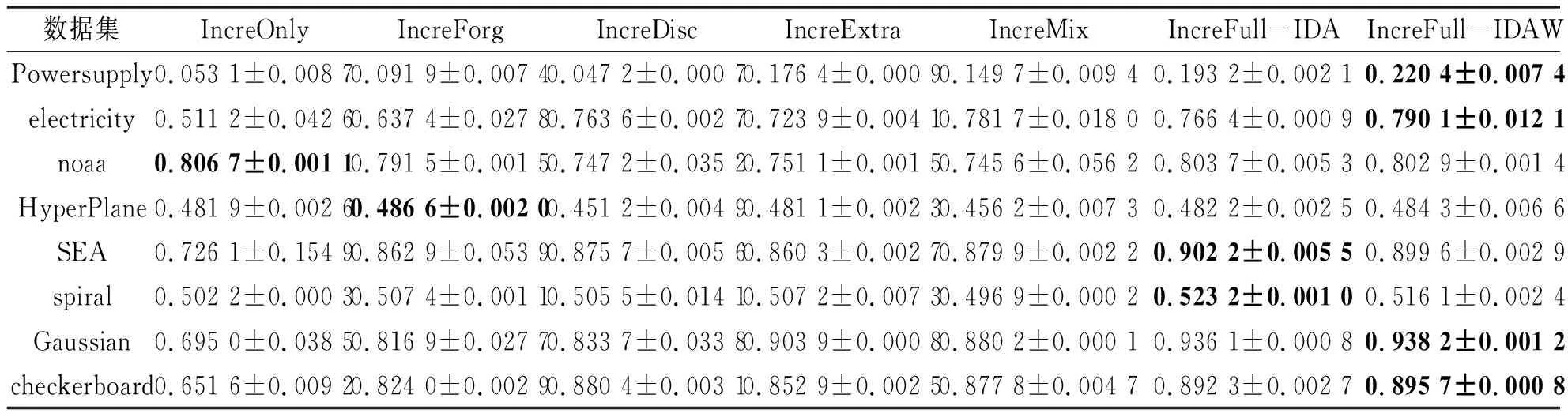
表3 各种算法的实验比较结果

从表3的实验结果中，可以得出以下结论：

(1)增量离散化策略确实可以有效地解决数据流中的概念漂移问题，这一结论可以通过比较IncreMix与IncreOnly算法的实验结果而得出，也与文献[13]的结论是完全吻合的.同时，从上述两类算法的实验对比结果中也可以看出：在noaa, HyperPlane和spiral等3个数据集上，融合了离散化特征后的分类精度反倒出现了下降，认为其可能与离散化自身的信息损失特点有关，在这几个数据集上，这一特点可能被放大了.

(2)采用在在线学习模型上添加遗忘机制的策略确实能缓解概念漂移的影响，这一结论可以通过比较IncreForg和IncreOnly算法的实验结果的得出.但同时也发现：采用遗忘机制能起到的性能提升作用非常有限的，其远不如IncreFull-IDA和IncreFull-IDAW.出现这种现象的原因可能在于：IncreForg采用的是固定的遗忘系数，而没有考虑概念漂移是否发生，发生时漂移的幅度又是多大这两个重要因素.当然，可以通过加入概念漂移检测模块来动态调控遗忘系数，相信学习性能会有一定的提升，但也必然会大幅增加算法的时间开销.

(3)与IncreOnly算法的实验结果相比，IncreExtra算法在大部分数据集上有明显的性能提升.尽管IncreExtra遗弃了增量离散化的过程，但其仍然整合了不算精确的高层结构特征，显然，这些特征是有助于改进模型质量的.原因可能有以下两方面：一是这些高层结构特征尽管不够精确，但仍能在一定程度上反应数据的全局与局部分布；二是尽管没有执行增量离散化过程，增量聚类技术也可能在一定程度上实现对概念漂移的自适应，从而提升学习性能.

(4)所提出IncreFull-IDA和IncreFull-IDAW算法在大部分数据集上，其分类性能要显著优于其它5种算法，再次表明了利用增量离散化来跟踪数据漂移，利用增量聚类来描述数据潜在的内部结构，利用结构特征抽取来提取高层结构特征的策略在解决漂移数据流建模问题上是有效的和可行的.

(5)对比IncreFull-IDA算法，IncreFull-IDAW算法在大部分数据集上都获得了或多或少的性能提升.这与两种算法的离散区间跟踪密度直接相关，IncreFull-IDA算法是间歇性随机对离散化区间进行跟踪，而IncreFull-IDAW算法则能实现对离散化区间的完全跟踪.事实上，文献[13]指出：IDA策略可适应逐渐演化的概念漂移和循环发生的概念漂移，但不适应突发的概念漂移，而IDAW策略对所有的概念漂移类型均适用.

2.4 参数讨论

文中算法中，有两个重要的参数可能会极大地影响到学习模型的最终质量，一是增量离散化的区间数m，另一个则是增量聚类的类簇数k.不失一般性，以Powersupply和SEA数据集为例，分别测试了所提出的两种算法随上述两参数变化而产生的性能变化.其中，m的取值变化区间为[4,12]，变化步长为2，而k的取值变化区间为[3,11]，变化步长为1.性能随参数变化结果如图3.

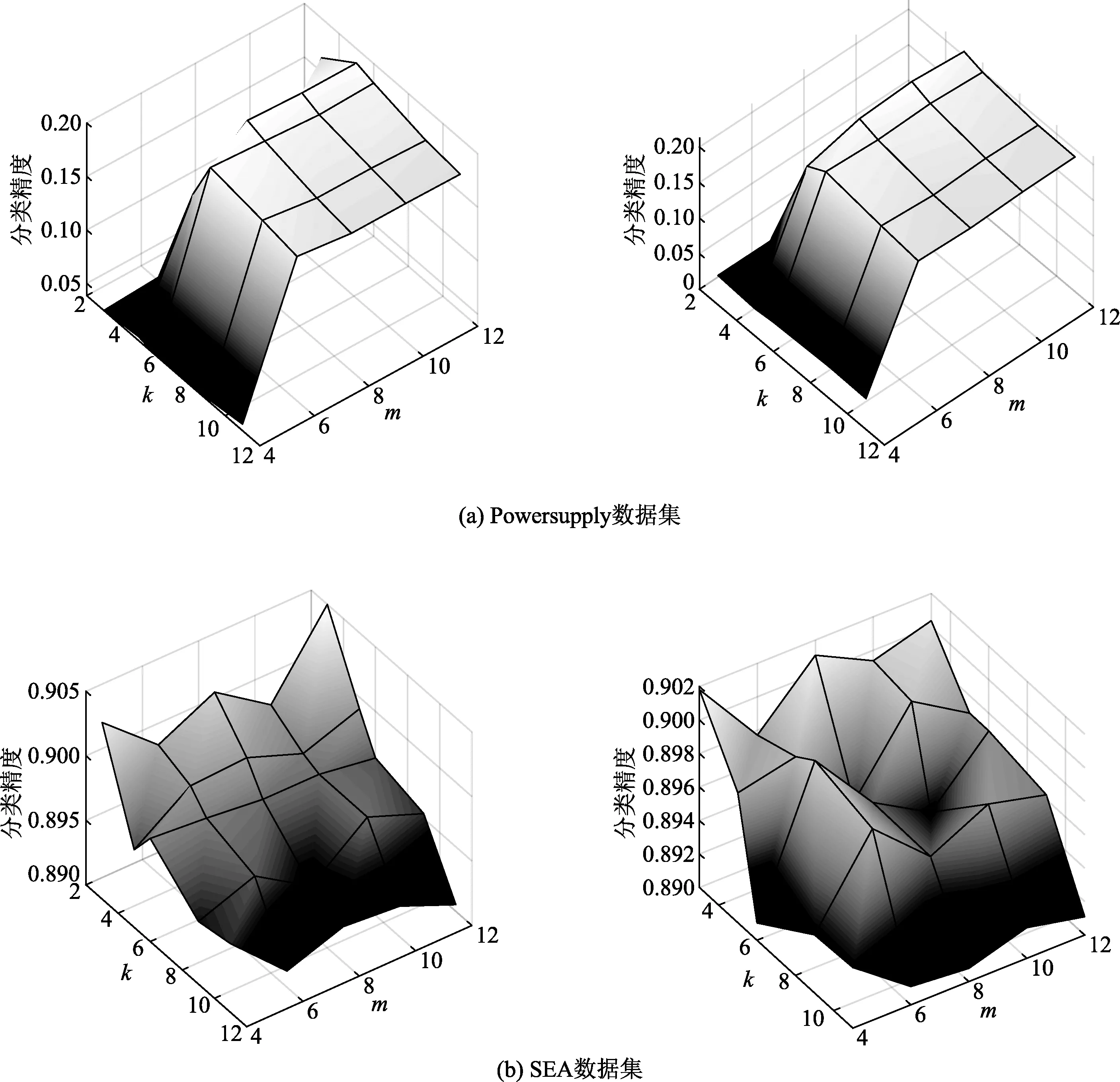
图3 文中算法随参数m与k的变化而产生的性能

从图3可以看出，尽管性能曲面的变化存在一些波动，但仍能反映出一定的规律.对于参数m，当其取值较小时，模型的性能通常较差，这主要是因为m的取值直接关系到了接下来增量聚类的特征空间大小，若其取值过小，则可能会导致增量聚类对数据内在结构描述的不够精确，必然会降低模型的质量.当m的取值逐渐增大时，模型的性能将会随之提升并逐渐趋于稳定.当然，取一个较大的m值尽管可以充分地保证建模的质量，但也存在时间复杂度过高的问题，可能会与在线学习的实时性需求相冲突，故建议在实际应用中对该参数取一个适中值即可.对于k的取值，发现两个数据集反馈回了完全不同的规律，在Powersupply数据集上，当k值过小时，学习算法的性能非常差，而在SEA数据集上，k值取为3反而保证了最好的模型质量.对比这两个数据集的描述信息，不难发现：Powersupply数据集包含24个类别，而SEA数据集只有两个类别.由于局部的结构特征可表示为类簇中的每类样本占比，因此，在类别数较多的数据集上，若聚类数设置的过小，则不能充分描述数据的结构，进而导致结构特征的提取缺乏精确性，从而降低学习算法的性能；而在类别数较少的数据集上，若聚类数设置的过大，又会导致对数据深层内在结构的过份解读，同样会影响算法的泛化性能.建议在实际应用中，根据数据中的具体类别数来设置对应的k值.

2.5 运行时间比较

测试各种比较算法在每个数据集上运行时间，结果可参见表4.

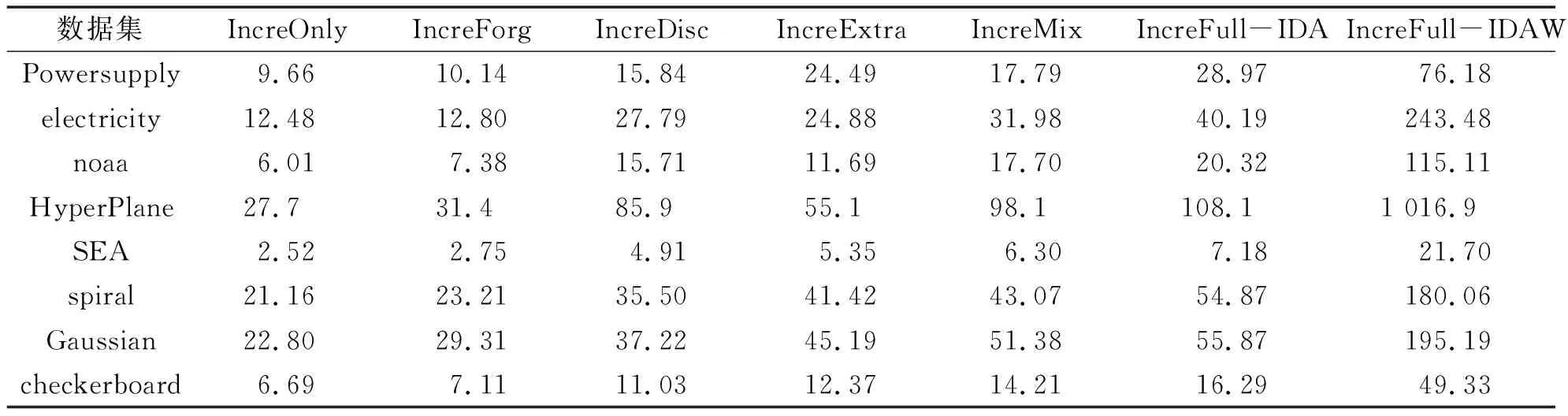
表4 各种算法的运行时间比较

从表4的结果可以看出：

(1)IncreOnly算法最为省时，原因在于该算法只实现了学习模型的动态更新，而省略了所有中间的处理步骤.

(2)相比于除IncreOnly外的其它算法，IncreForg算法通常都要更为省时，这与该算法采用固定遗忘系数，而未采用概念漂移检测模块有关.

(3)增量离散化和增量聚类都是较为耗时的数据处理过程.比较IncreDisc 和IncreExtra算法的运行时间结果，不难发现：当数据中的特征数较多时(如HyperPlane，electricity和noaa数据集)，增量离散化要普遍比增量聚类更耗时，而当数据中的特征数很少时，增量离散化通常要比增量聚类更省时.

(4)用于建模的特征向量的长短也会直接影响到算法的时间复杂度.特征向量越长，所需的运行时间往往也会越多，该结论可通过比较IncreDisc 和 IncreMix算法的运行时间结果直接得出.

(5)文中所提两种算法中，IncreFull-IDAW显然要比IncreFull-IDA更耗时.这是因为二者对离散区间的跟踪密度不同，IncreFull-IDAW算法每接收到一个新样本时，均会对离散区间进行跟踪，而IncreFull-IDA算法则是间歇性的随机跟踪.在实际应用中，若对实时性的需求很高，建议采用IncreFull-IDA算法，而若对实时性要求不高，则建议采用IncreFull-IDAW算法.