排放限制下考虑风浪的邮轮航速研究
2022-04-21闵德权田玉玲
闵德权,董 洁,田玉玲
(大连海事大学 交通运输工程学院,大连 116026)
近年来,随着邮轮旅游的日益发展和成熟,其在经济获利的同时也伴随着环境方面的各种问题.排放控制区(emission control area,ECA)是推动绿色航运发展下的产物,为遵守ECA的相关法规,可在ECA内改用低硫燃油来达到排放要求,然而低硫燃油价格较高,且燃油成本约占总运营成本的2/3,因此使用低硫燃油给邮轮公司造成一定的经济压力.文献[1]研究表明,与始终以恒定速度航行相比,区分ECA内外速度的航行方式可节省燃油成本,这种节约成本的方式在低硫燃油价格较高时更为明显.文献[2]通过对ECA内外的航速进行优化,使航行成本和时间得到有效折中.文献[3]在航程时间和船期不变的前提下,研究船速变化对SO2总排放量和燃油成本的影响,得出在ECA内外进行航速优化可以节约较多成本.
CO2排放过多导致全球平均气温上升,危及人类的生命和生活,由此CO2成为温室气体中削减与控制的重点.2020年的9月,在联合国大会上我国作为全球CO2排放第一大国承诺,力争在2030年实现碳达峰,2060年实现碳中和.在减少CO2排放量的手段中,碳税政策在各个国家普遍被采用.由于船舶碳排放量与航速成比例关系以及采取“多排多征”的原则,降低船舶航速是减少碳排放最直接有效的方法.文献[4]指出航海业的碳税制度可以促进企业发展、维系企业经济外环境、规避不良风险,对于航运业的绿色发展具有重要作用.文献[5]构建考虑碳税成本的航线配船和航速优化的数学模型,得出随着碳税税率的提高,船舶航速逐渐降低,航线配船数量逐渐增加,船舶总运营成本增加明显.文献[6]考虑燃油价格的变动和CO2的排放,对船舶燃油补给策略与航速进行优化求解,建议班轮企业合理设置燃油价格模糊程度和碳税税率.
关于航线研究的主体都是邮轮[7-8],考虑了排放控制区,但其忽略了碳税成本对于航速的影响,尤其是在当下大力减排温室气体的时代背景下,碳税成本的考虑必不可少.文献[9]综合考虑了排放控制区和碳排放的限制,选择3条具有代表性的班轮航线进行优化求解,但其对于航速的优化研究忽略了风浪干扰力的影响.在考虑风浪的气象条件下,对船舶航速进行研究的文献发现[10-11],航速优化研究主要集中在班轮运输上,较少以邮轮为研究主题,且考虑影响航速的因素较少.在综合考虑ECA、碳税成本、燃油成本以及各港口的到港时间限制,对邮轮航速的研究少之又少.鉴于此,文中提出一个有到港时间限制,同时考虑ECA的通航限制和风浪的干扰,以航速为决策变量,以燃油消耗成本和碳税成本总和最小为目标函数的混合整数非线性规划模型,通过MATLAB软件进行优化求解,以丰富和完善邮轮航速优化理论.
1 干扰力模型
1.1 风干扰力模型
邮轮在海上航行时会受到风的影响,对其上层建筑产生一定的干扰力,从而影响邮轮的航行速度.由于邮轮在航行过程中,其前进的速度远大于横向速度,故在分析风干扰力时,仅考虑艏艉方向上的平均风压力为[12]:
(1)
式中:ρa为空气密度;A1为邮轮水线以上的正投影面积;vow为相对风速;∂1为相对风速与船首的夹角;Cx(∂1)为艏艉方向上的风压力系数.
Cx(∂1)=CF·cos ∂2·(A2·sin2∂1+A1·cos2∂1)/A1
(2)
式中:CF为风压合力系数;∂2为风压合力角;A2为水线以上的侧投影面积.
∂2=(1-0.15×(1-∂1/90)-0.80×
(1-∂1/90)3)×90
(3)
CF=1.325-0.05×cos(2×∂1)-0.35×
cos(4×∂1)-0.175×cos(6×∂1)
(4)
1.2 波浪干扰力模型
波浪通常分为不规则波和规则波,由于不规则波的计算方法比较困难,故文中波浪干扰力模型主要考虑规则波,利用文献[13]提出的波浪干扰力模型:
(5)
式中:X为x方向上的波浪干扰力;ρw为海水密度;g为重力加速度;L为船长;H为波浪的振幅;λ为波长;χ为波向角;Cx(λ)为试验系数.
Cx(λ)=0.05-0.2×(λ/L)+0.75×
(λ/L)2-0.51×(λ/L)3
(6)
振幅H通过回归公式计算:
(7)
式中,vw为绝对风速.
1.3 静水航速模型
假设邮轮在风浪气象条件下的推进功率与静水中的推进功率相同,则有效推进功率Pe对静水中邮轮航速vsw和静水阻力Fsw(v)与风浪影响下的实际航速vr和总阻力FT(v)存在关系,即:
Pe=FT(vr)vr=Fsw(vsw)vsw
(8)
邮轮在风浪影响下航行产生的有效推进功率与克服风浪干扰力产生的功率之和为总的推进功率[11].
FT(vsw)·vsw=(Fsw(vsw)+FAdd(vsw))·vsw=
FT(vr)vr+FAdd(vsw)·vsw
(9)
CR+FAdd(vsw)×vsw
(10)
(11)
(12)
式中:FAdd(vsw)为艏艉方向上所受的干扰力;S为浸水面积;CR为船舶阻力因数.
2 问题描述与建模
2.1 问题描述
邮轮公司面对当下船舶废气排放限制的通航要求、燃油价格不断攀升带来的成本压力以及新冠疫情对航运经济带来的沉重打击,通过调整航速来降低运营成本,是高能耗邮轮公司的当务之急.文中针对有到港时间限制的固定航线提出一个航速优化模型,以燃油消耗成本和碳税成本总和最小化为目标,考虑风浪气象条件的影响,决策邮轮每条航段上ECA区域内、外的航速.
2.2 模型假设
(1)气象条件中风为恒风,波浪为规则波.
(2)忽略邮轮自身在航行过程中重量的变化,以出发时的重量为准.
(3)港口挂靠顺序已确定.
2.3 模型参数
A:港口集合{1,2,...,n,n+1},1和n+1都为始发港口;
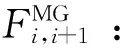
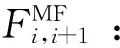
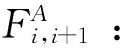
Fi:在港口i停靠时邮轮消耗的MGO燃油量,t;
cG:MGO价格,美元/t;
cF:HFO价格,美元/t;
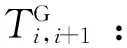
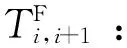
Ti,i+1:从港口i到港口i+1,邮轮航行时间,h;
Ti:邮轮在港口i的停靠时间,h;
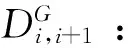
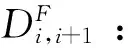
vmin:航线上速度的最小值,kn;
vmax:航线上速度的最大值,kn;
λG:MGO的碳转化系数;
λF:HFO的碳转化系数;
e:碳税税率,美元/t;
EMCO2:邮轮的CO2排放总量,t;
di:邮轮到达港口i的时间,h;
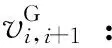
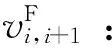
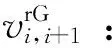
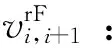
Sik:邮轮第k个挂靠港口是否为港口i,是等于1,否等于0;
2.4 参数关系
2.4.1 邮轮航行时间,h
就图书馆资源来说,高等学校可以依据共享的资源数量和质量来要求共享者提供相应的建设成本和运营成本;又比如实验室以及设备,也可以根据共享的理念,拥有丰富资源的高校可以给资源少的高校提供资源,只需要提供相应的成本补偿即可以确保利益不受损。最后,就个人而言,教师如果有资历可以参与外聘工作,同时可以得到受聘用高校给付的劳动报酬。应建立和完善有偿机制,从而对有偿支付使用进行统一的规定,防止乱收费现象的发生。收费主要是依据用于资源自身的维护、维修的需要,资源管理者的劳务费或者是购置新的资源等方面制定的,并且应避免以盈利为目的,在此之后还应该将收费的标准上报学校和相关部门备案,同时应接受公开监督和检查。
1)邮轮在ECA内航行时间,h
(13)
2)邮轮在ECA外航行时间,h
(14)
3)邮轮总航行时间,h
(15)
2.4.2 航行过程中主机燃油消耗,t
1)ECA内燃油消耗,t
(16)
式中:SFCMG为主机燃烧MGO的油耗率,g/(kW·h);PM为邮轮主机发动机功率,kW.
SFCMG=SFCMGbe·(0.455×EL2-0.71×EL+1.28)
(17)
(18)
式中:δw为速度-功率校正系数,具有新颖推进布局的邮轮的δw为0.7,其余邮轮的δw为1;ηw为天气校正系数;ηf为污垢校正系数;PMref为主机的参考功率,kW;t/tref为吃水系数,定义为邮轮登记的最小吃水与最大吃水之比;Vref为速度的参考值,即运营航速,kn;m为吃水比指数;n为速度比指数.
2)ECA外燃油消耗,t
(19)
式中:SFCMF为主机燃烧HFO的油耗率,g/(kW·h);SFCMFbe为主机燃烧HFO的基准油耗率,g/(kW·h).
SFCMF=SFCMFbe·(0.455×EL2-0.71×EL+1.28)
(20)
(21)
2.4.3 航行过程中辅机燃油消耗,t
(22)
(23)
式中:SFCAbe为辅机燃烧MGO的基准油耗率,g/(kW·h);PAref为辅机的参考功率,kW.
2.4.4 停泊过程中的燃油消耗,t
Fi=Ti·e(-21.9+2.8×ln(GW)-1.15×ln(bts)-0.36×Delec)
(24)
式中:GW为总载重吨,t;bts为铺位总数;邮轮采用柴油-电力配置时Delec为1,否则为0.
2.4.5CO2排放量,t
(25)
2.5 模型构建
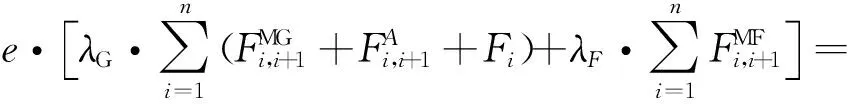
(26)
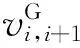
(27)
d1=0Ti,i+1
(28)
di+Ti+Ti,i+1=di+1i∈A
(29)
(30)
Sik∈{0,1}i∈A,k∈K
(31)
目标函数式(26)为最小化燃油消耗成本和碳税成本.约束式(27)为邮轮的航速约束.约束式(28~30)为邮轮到达港口的时间约束.约束式(31)为Sik为0-1决策变量.
3 实例验证与分析
采用的邮轮数据如表1.
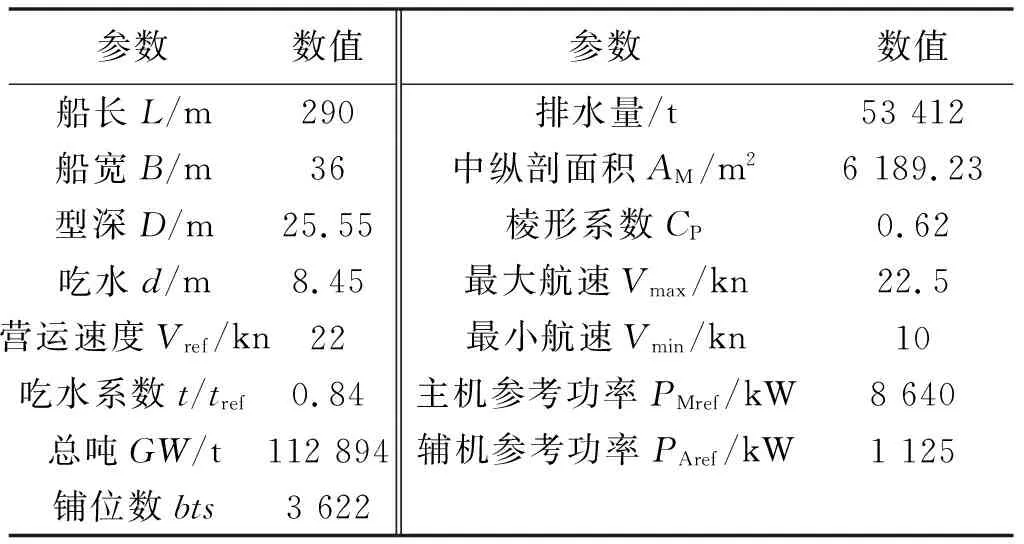
表1 邮轮数据
3.1 阻力系数计算
式(10)中的阻力系数CR由摩擦阻力系数Cf、剩余阻力系数Cr和粗糙度补粘系数ΔCAR组成.
CR=Cf+Cr+ΔCAR
(32)
(1)摩擦阻力系数
摩擦阻力系数采用国际船模试验水池会议(ITTC)提出的拟合公式为:
(33)
式中:Rn为雷诺兹系数,Rn=V·L/μ,μ为运动黏度.
(2)剩余阻力系数


图1 系数拟合曲线
Cr=a1·Fn3+a2·Fn4+a3·Fn5+a4·Fn6
(34)
(3)粗糙度补粘系数
粗糙度补粘系数可以通过表2获得.
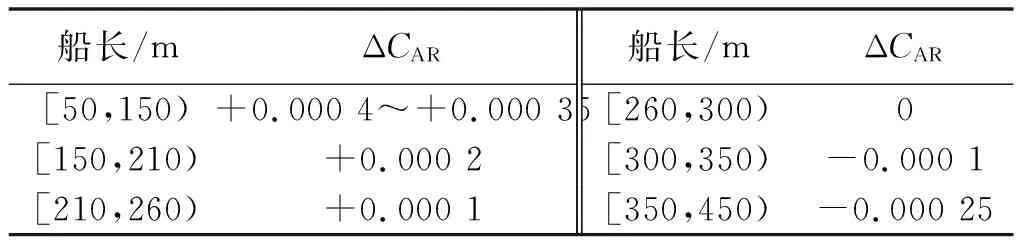
表2 粗糙度补粘系数表
3.2 数据采集
以新英格兰地区的邮轮航线为例,邮轮从美国纽约出发,依次经过加拿大哈利法克斯、加拿大悉尼、格陵兰岛努克、格陵兰岛纳诺塔利克、加拿大圣约翰,最后回到美国纽约.航线信息见表3.航线总长为5 849 n mile,ECA航段总长为1 606 n mile,ECA航段所占百分比为27.5.
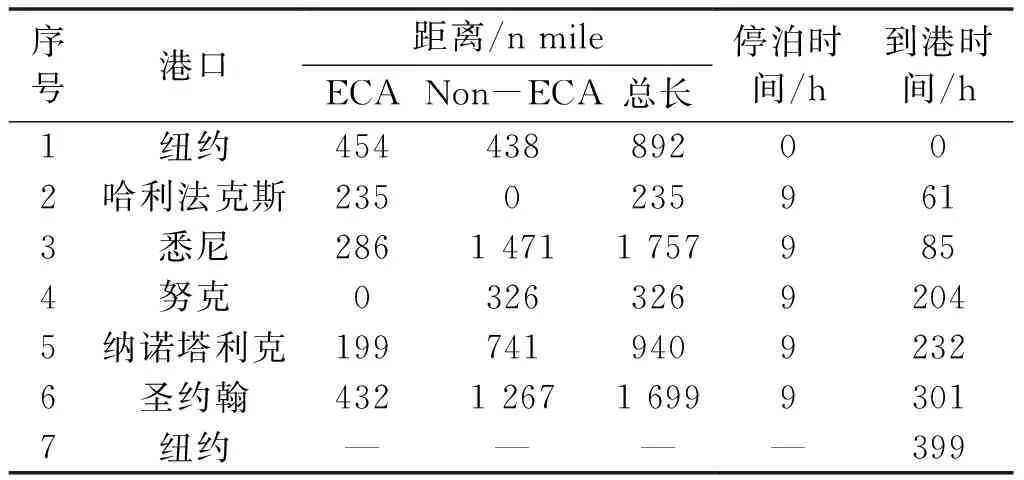
表3 航线数据
邮轮在两港之间通常不会是直达,而是通过多个航路点连接而成.整条航线划分为7个节点、27个航段以及28个航路点,具体航段划分见表4.航线中每个航段的航程、风向、风级和波向角,如表5.表5中航段编号带有“*”为ECA航段,否则为非ECA航段.
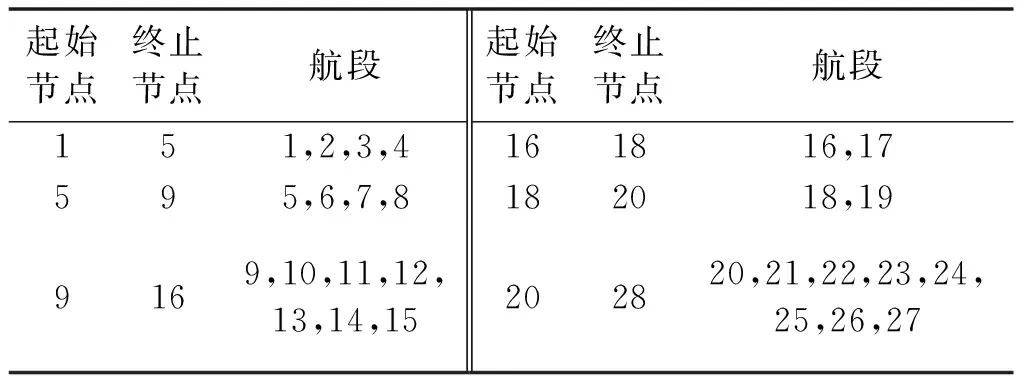
表4 航段划分
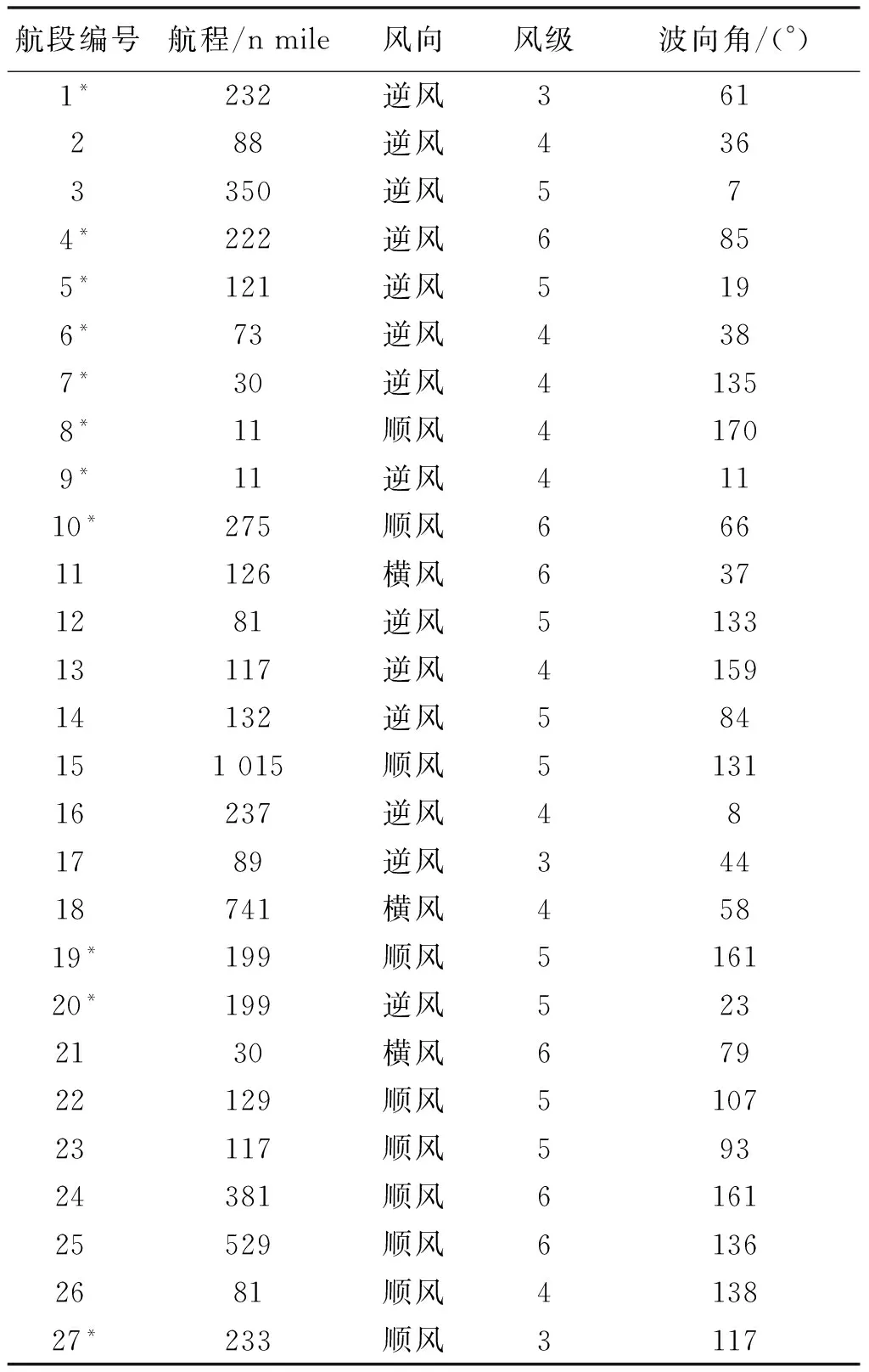
表5 航线信息
《Forth IMO GHG Study 2020》报告中相应的模型参数取值,如表6.

表6 模型参数取值
3.3 模型结果
3.3.1 优化结果分析
首先对优化之前的邮轮航行情况进行分析,结果如表7.邮轮实际航行全程中总目标成本为792 116.88美元,总燃油消耗成本为647 763.17美元,总碳税成本为144 353.71美元,总CO2排放量为4 511.05 t.由于ECA内使用的低硫燃油价格较高,故一般邮轮公司在航行时,会在ECA航段内使用尽量低的航速,然后通过提高ECA外航段的航速,来满足港口的时间窗要求.
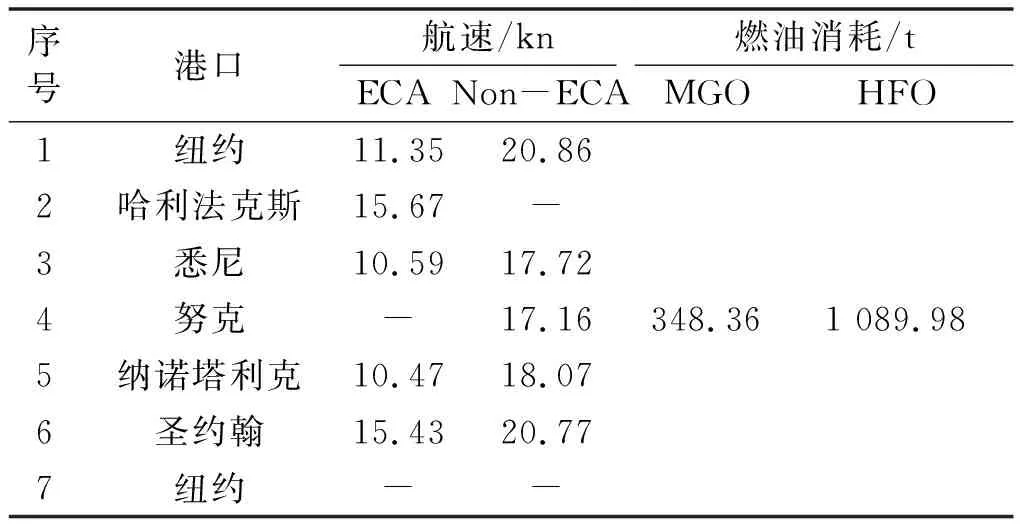
表7 邮轮航行情况
现进行优化求解,依据模型假设,取海浪波长为80%船长.基于上述模型和数据,运用MATLAB软件自编代码得到在风浪影响下满足目标函数最优的决策方案,总目标成本为736 143.47美元,总燃油消耗成本为610 648.40美元,总碳税成本为125 495.07美元,总CO2排放量为3 921.72 t,航速优化结果详见表8.由于邮轮是特殊的运输工具,为了方便游客进行观光旅游,保证优质的服务水平,其到达各个港口的时间一般在白天或合适的时间点.不同的航段其航速也不相同,且对应节点航段的ECA外的航速比ECA内的航速高.
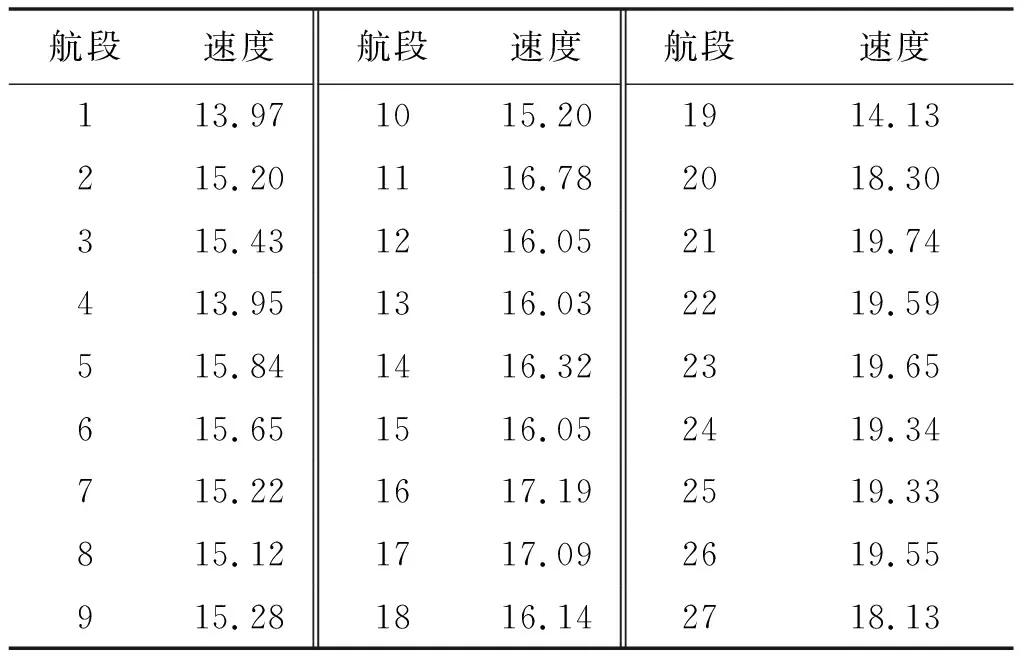
表8 模型计算结果
将优化前后的结果进行对比,总CO2排放量减少了589.33 t,降低了13%,总碳税成本减少了18 858.64美元,降低了13%,总燃油消耗成本减少了37 114.77美元,降低了6%.可以看出,在综合考虑了碳税成本、燃油消耗成本、排放控制区和风浪的影响时,结合邮轮的航向和航程,对航速进行合理的优化,可以达到减少目标函数的目的.
图2为优化之后实际航速与静水航速的对比图,可以看出:增速幅度最大的为第19航段,降速幅度最大的为第11航段,船舶增降速的比例与风向、风舷角、风速、船舶自身的航速、波向角众多因素有关,风向为顺风时,邮轮航速越小,风速越大,波向角越大,且风舷角越大邮轮增速越大.风向为逆风时,邮轮航速越小,风速越大,波向角越小,且风舷角越小邮轮降速越大.风向为横风时,邮轮航速越小,风速越大,波向角越小,且风舷角越小邮轮降速越大.
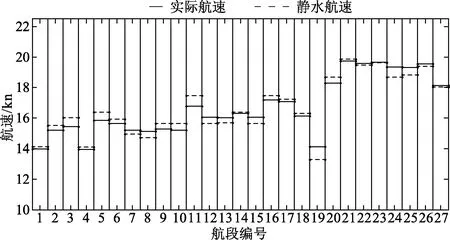
图2 航速优化结果
在进行风浪干扰力的数据计算时发现,当风浪来自邮轮正横前时,风干扰力随着风舷角的增大为先增大后减小,浪干扰力随着波向角的增大而逐渐减小,此时风浪的干扰力均为阻力;当风浪来自邮轮正横后时,风的干扰力随着风舷角的增大为先增大后减小,浪的干扰力随着波向角的增大而逐渐增大,此时风浪的干扰力均为推力.当风浪来自邮轮正横前时,风浪总合力随着风舷角的增大而逐渐减小,当风浪来自邮轮正横后时,风浪总合力随着风舷角的增大而逐渐增大.同时随着风速的增大,其风浪干扰力增大或减小的幅度逐渐增大.
3.3.2 碳税成本对航速的影响
对风浪影响下的邮轮航速研究是在排放限制的前提下,因此文中对排放限制的影响作用进一步分析,在目标函数不考虑碳税成本下对该邮轮航线的航速进行优化求解,并将航速优化结果与考虑碳税成本的结果进行对比分析,见图3.
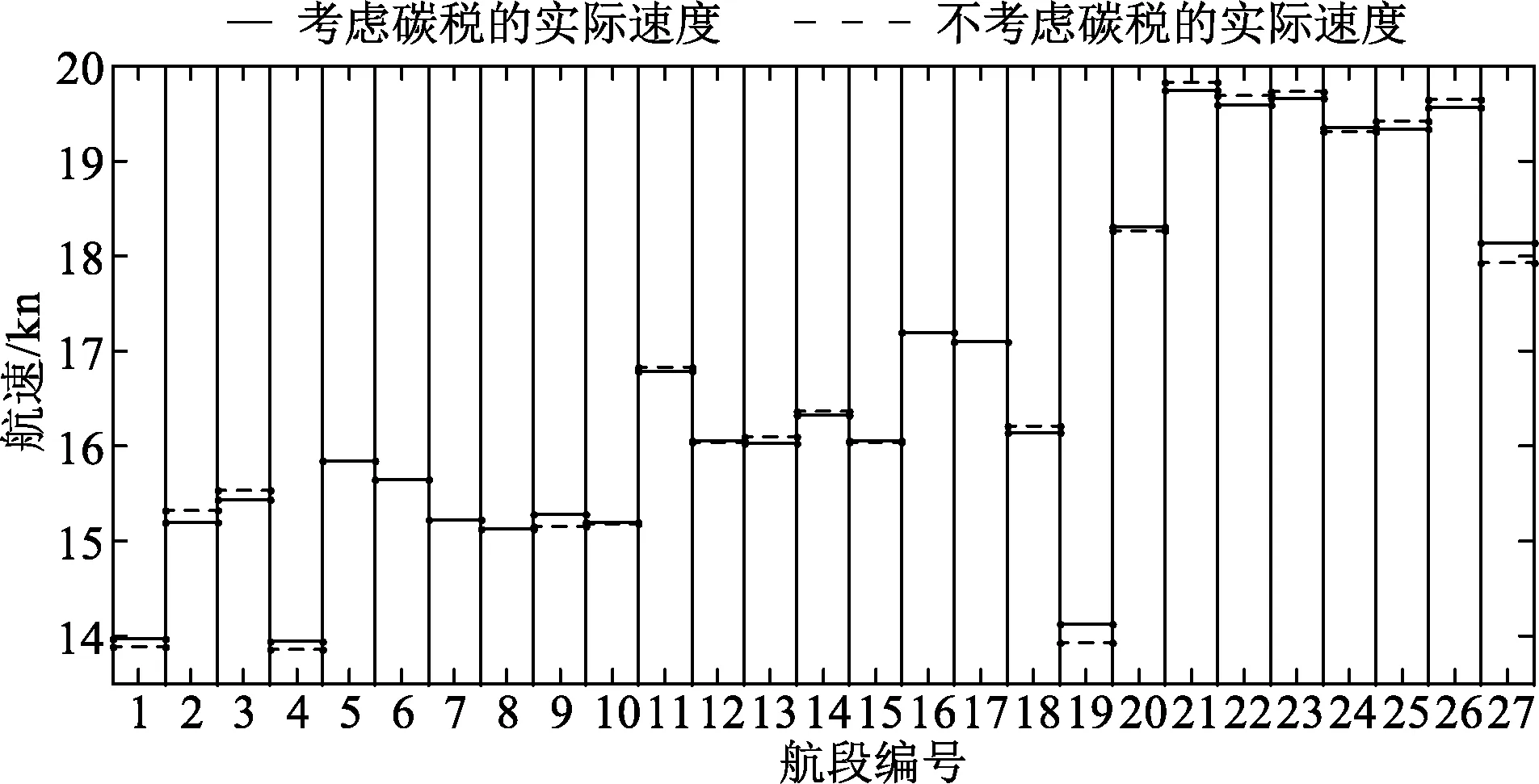
图3 航速对比结果
从图3中可以看出,不考虑碳税成本的ECA航段的航速大多比考虑碳税成本的航速要小;不考虑碳税成本的非ECA航段的航速大多比考虑碳税成本的航速要大,由于ECA内燃油价格比ECA外燃油价格要贵得多,故在不考虑碳税成本的前提下,会通过降低ECA内航速来减少ECA内的燃油消耗,从而使总的目标成本较小.
3.3.3 模型的适用性验证
为了验证该模型具有较好的适用性,现另选一艘邮轮,基于上述的航线信息和模型进行优化求解.为了后文分析时便于区别,原来案例中的邮轮为1号邮轮,新对比的邮轮为2号邮轮.2号邮轮数据见表9.
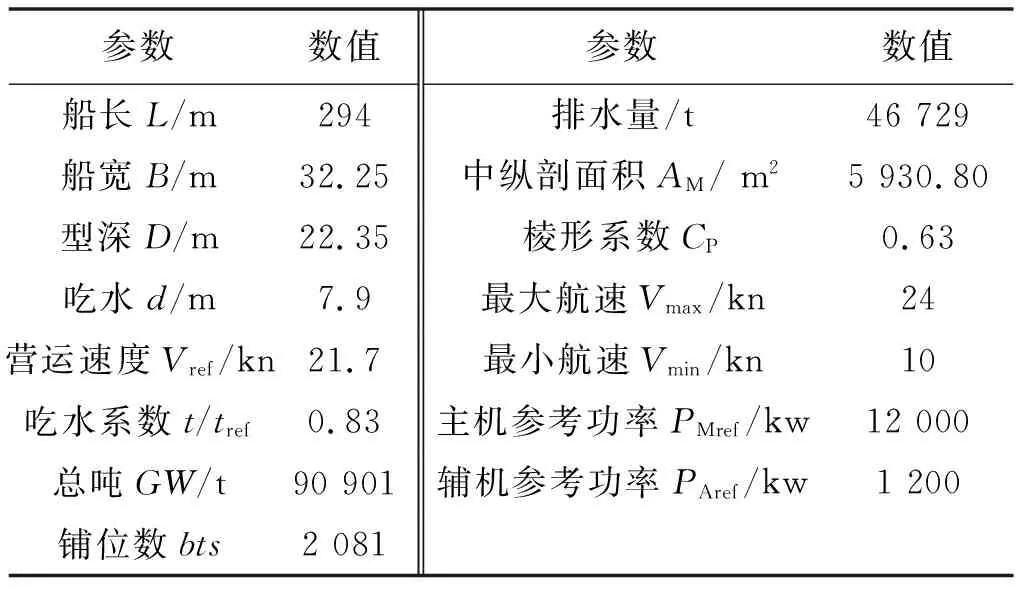
表9 邮轮数据
根据2号邮轮的相关数据在IMO的温室气体排放研究报告中查找相应的模型参数,其模型参数与1号邮轮的模型参数值相同.基于表9的数据以及模型对航速进行优化求解,得到在该条航线上对于2号邮轮满足目标函数最优的决策方案,总目标成本为986 603.73美元,总燃油消耗成本为811 856.82美元,总碳税成本为174 746.91美元,总CO2排放量为5 460.84 t,航速优化结果见表10.

表10 2号邮轮模型计算结果
图4为2号邮轮优化之后的实际航速与静水航速之间的对比图,在同一条航线上,1号邮轮与2号邮轮的实际航速和静水航速之间的增减趋势是一致的.通过对比1号邮轮与2号邮轮的优化结果发现,2号邮轮的各项成本均比1号邮轮的对应成本大,主要是因为两个邮轮的主副机功率、营运速度、受到的风浪干扰力不同.基于上述的分析,可以看出本文所建立的模型对于邮轮的优化具有较强的适用性,能够较好的获得最优决策方案.
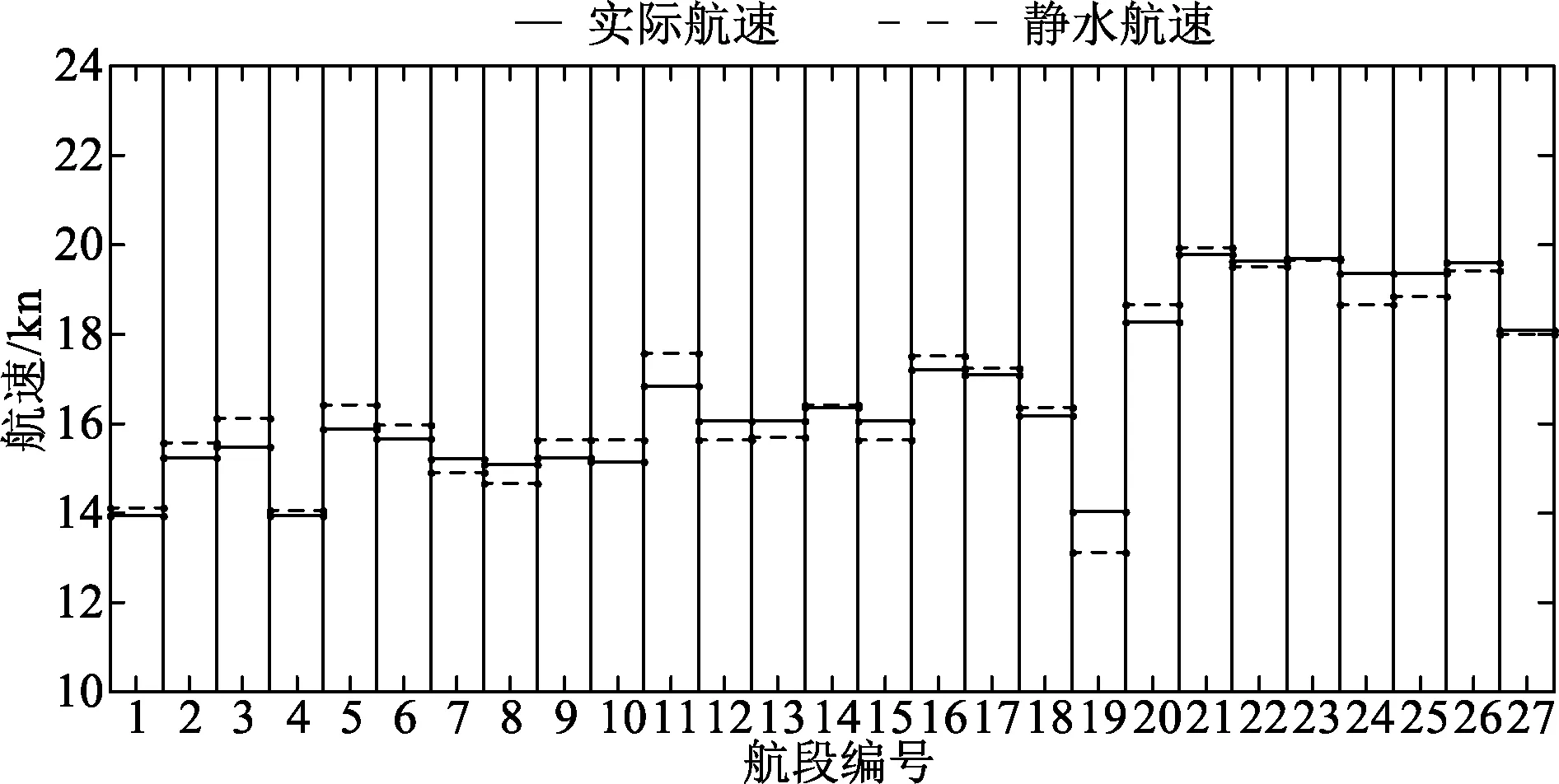
图4 2号邮轮航速优化结果
4 结论
(1)邮轮航速在风浪影响下的增减幅度与邮轮本身的航速、风向、风速、风舷角、波向角有关.风向为顺风时,邮轮航速越小,风速越大,波向角越大,且风舷角越大邮轮增速越大.风向为逆风或横风时,邮轮航速越小,风速越大,波向角越小,且风舷角越小邮轮降速越大.
(2)风浪干扰力与风舷角之间有着密切的关系.当风浪来自邮轮正横前时,风浪总合力随着风舷角的增大而逐渐减小,当风浪来自邮轮正横后时,风浪总合力随着风舷角的增大而逐渐增大,且随着风速的增大,其风浪干扰力增大或减小的幅度逐渐增大.
(3)考虑碳税成本对邮轮航速有较小的影响,在ECA航段考虑碳税成本时其航速一般比不考虑碳税成本的航速要大,在非ECA航段考虑碳税成本时其航速一般比不考虑碳税成本的航速要小.
(4)模型可以计算出不同风、浪条件下的邮轮最优航速,且具有较好的适用性,可为邮轮公司带来可观的经济效益和环境贡献.
