基于邻域区分度的不完备混合数据属性约简方法

孙 林，李梦梦，徐久成

(河南师范大学 计算机与信息工程学院，新乡 453007)

随着大数据处理技术的发展，属性约简在数据挖掘、机器学习等领域中发挥着非常重要的作用[1].在日常生产生活中，由于数据采集过程中存在测量误差、设备故障、人为遗漏等意外因素，导致出现大量的属性值缺失的不完备数据[2].在实际应用中，符号型和数值型混合的不完备决策系统也是一种常见的信息系统类型[3-4].邻域粗糙集理论[5]是一种处理混合型不完备决策系统的常用有效模型[6-7].文献[8]针对不完备混合型决策表，提出了一种基于邻域容差条件熵的邻域粗糙集特征选择算法.文献[3]结合Lebesgue测度和熵度量，提出了不完备混合邻域决策系统的特征选择算法.但是，上述处理不完备数据的属性约简模型仍存在没有实施更有效的度量机制，未能精准评估属性集之间的依赖关系，以及算法效率偏低等问题.

信息系统的区分度是一种非常有效的属性集度量函数.文献[9]定义可区分度来度量信息系统中属性重要性，设计了一种启发式约简算法，并通过实验证明了基于区分度属性约简算法的高效性.文献[10]基于矩阵构造区分度，提出了一种增量式属性约简算法.文献[11]针对混合数据提出了基于邻域区分度的增量式属性约简算法.因此，区分度是构造属性约简的一种重要度量方法，不仅可以更加准确地度量属性集之间的依赖关系，而且具有计算时间复杂度低的优势[11].但是，目前还未有利用区分度进行不完备混合数据属性约简的研究，因此，将文献[9]的符号型信息系统中的区分度概念推广到不完备混合型信息系统中.

首先利用邻域粗糙集模型既能分析数值型数据，又能处理符号型与数值型的混合数据的优势，针对不完备混合数据，构建不完备混合邻域决策系统；基于Relief 算法的diff函数定义新的距离函数，分别处理离散型属性、数值型属性和属性值缺失情况；并给出邻域、邻域容差关系、邻域上下近似集等概念，进而构建不完备混合数据的邻域粗糙集模型.然后，在不完备混合邻域决策系统中，基于不完备混合数据的邻域粗糙集模型定义区分关系、邻域区分度和相对邻域区分度概念，理论证明了相关性质及单调性定理.最后，基于相对邻域区分度给出属性约简集、内部与外部属性重要度以及核属性等定义，设计基于邻域区分度的不完备混合数据属性约简算法.5个低维UCI数据集和3个高维基因数据集上的仿真实验结果表明，所提出的属性约简算法在处理不完备混和数据集上具有较好的分类性能.

1 不完备混合数据的属性约简方法

1.1 不完备混合数据的邻域粗糙集

假设不完备混合邻域决策系统表示为IMNDS=，其中U={x1,x2,…,xm}；C=C1∪C2为条件属性集，其中C1为符号型属性子集，C2为数值型属性子集；D为决策属性集，并且C∩D= Ø；V代表各个属性的值域；f是U×A→V的映射函数，并且存在f(a,x)=*，即属性存在缺失值；Δ→[0, ∞]是距离函数；δ是邻域半径参数且0 ≤δ≤ 1.

传统的欧氏距离忽略了不同属性之间的差别，而Relief算法[12]可以通过特征对近距离样本的区分能力进行评价，原因在于diff函数能有效地找到最近邻的样本集.因此，使用Relief算法中的diff函数定义一种新的距离函数作为邻域粗糙集的距离函数.

定义1在IMNDS= 中，对于xi,xj∈U，a∈C，使用diff函数计算两个样本在属性上的差异程度，分3种情况描述：

(1)在处理离散型属性时，距离函数为：

(1)

(2)在处理数值型属性时，距离函数为：

(2)

(3)在处理属性值缺失时，距离函数为：

(3)

定义2在IMNDS=中，B⊆C，a∈B，对于xi,xj∈U，那么δB(xi)表示xi关于B的邻域为：

δB(xi)={xj|xj∈U,diff(a,xi,xj)=

ΔB(f(a,xi),f(a,xj))≤δ}

(4)

定义3在IMNDS=中，B⊆C，a∈B，那么关于B的邻域容差关系和xi关于B邻域容差类分别为：

f(a,xj)∨f(a,xi)=*∨f(a,xj)=

*∨Δ(f(a,xi),f(a,xj))≤δ}

(5)

(6)

定义4在IMNDS= 中，B⊆C，xi∈X⊆U，那么B关于X的邻域上近似与下近似集分别为：

(7)

(8)

1.2 不完备混合数据的邻域区分度

定义5在IMNDS=中，B⊆C，那么B确定的区分关系表示为：

DIS(B)={(xi,xj)∈U2|∃a∈B,f(a,xi)≠f(a,xj)}

(9)

依据文献[11]定义2的原理，从上述定义5可知，在不完备混合邻域决策系统中，区分关系与不可区分关系是相反的且是互补的，在此基础上构建邻域区分度的概念.

定义6在IMNDS=中，B⊆C，a∈B，xi∈U，那么a在该系统下的邻域区分度为：

(10)

性质1在IMNDS= 中，B⊆C并且B为符号型属性集，a∈B，那么该邻域区分度为：

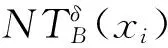
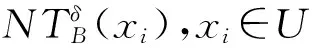
(11)

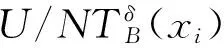
证明：由定义7可以直接得到

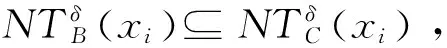
所以，可知

即NDDB(D)≤NDDC(D).

1.3 基于邻域区分度的属性约简算法

定义8在IMNDS=中，若R⊆C是属性约简集，那么下式一定成立：

NDDC(D)=NDDR(D)

(12)

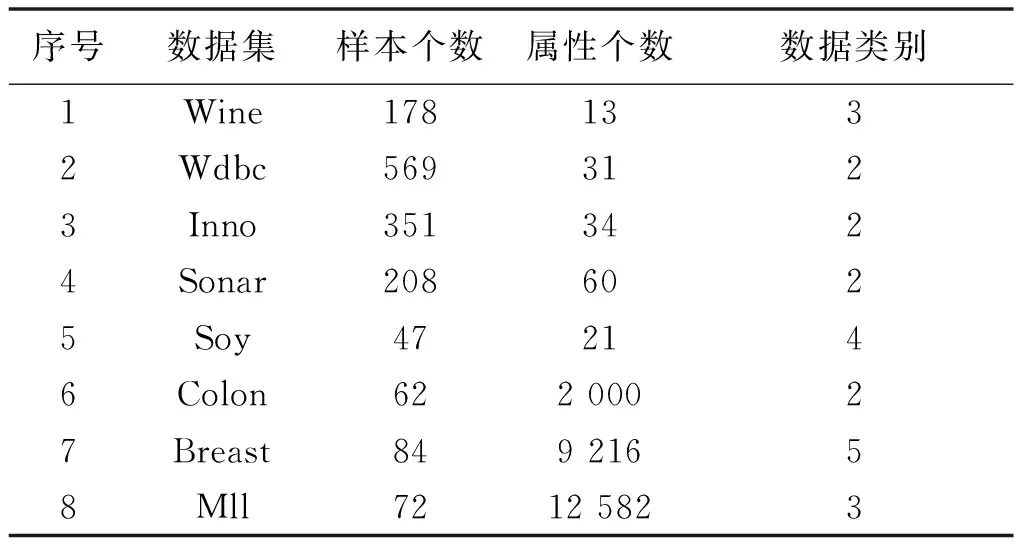
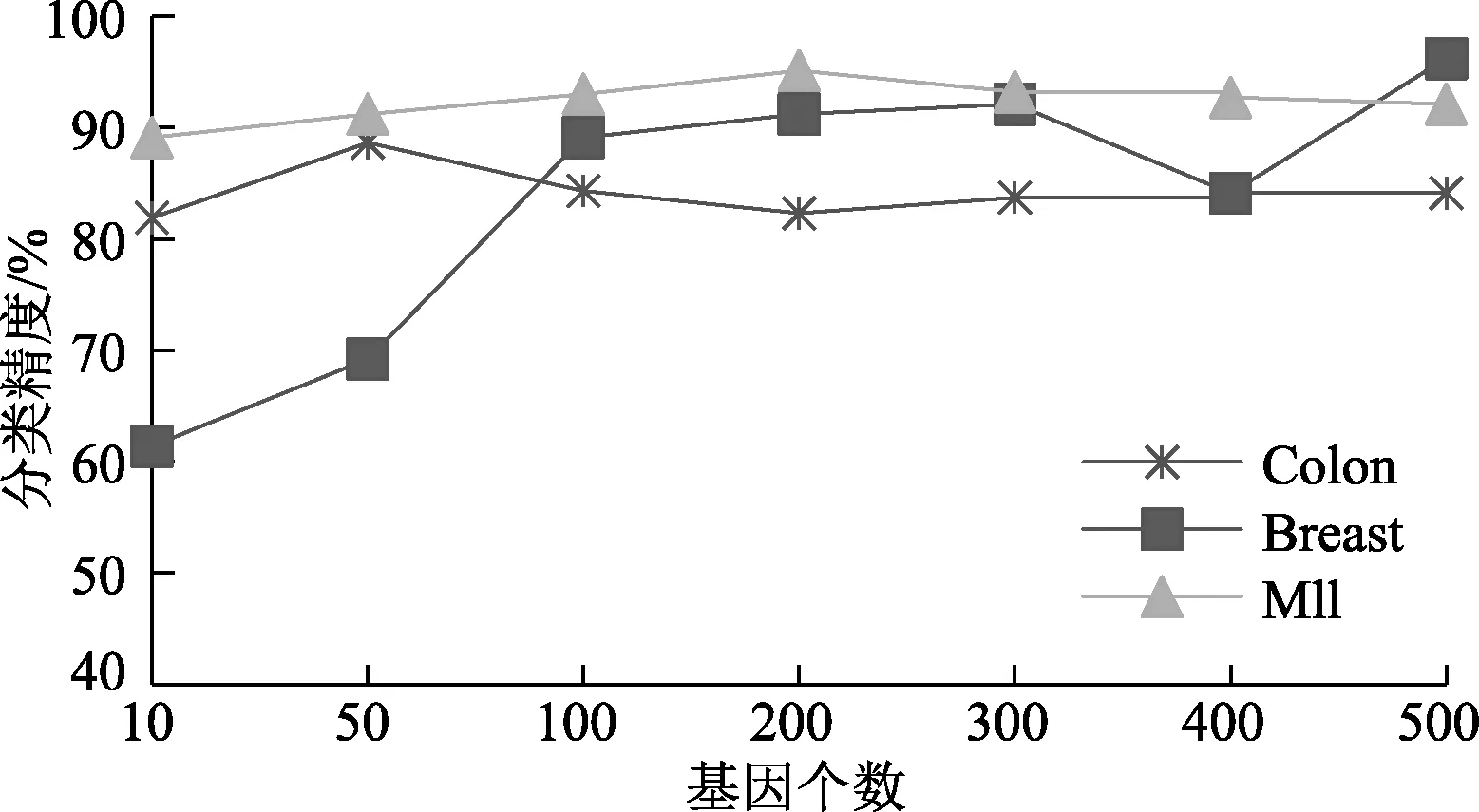
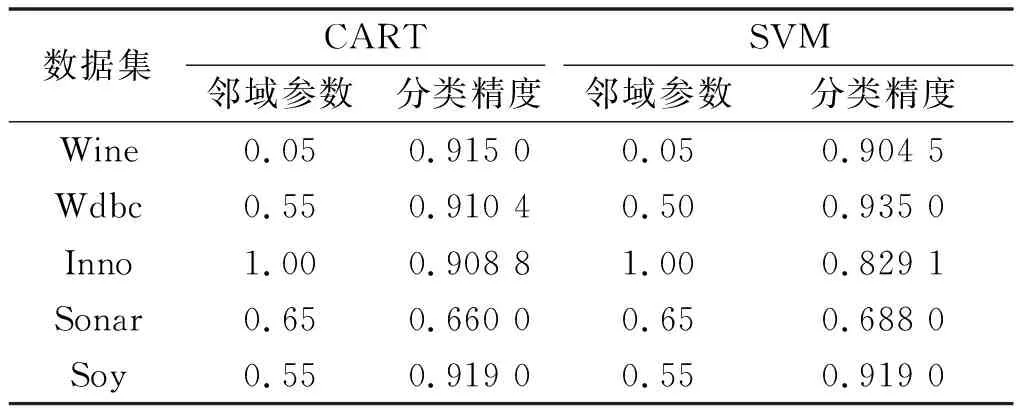
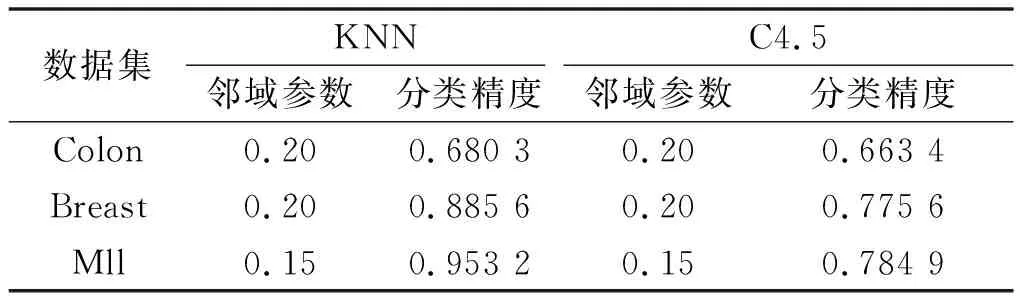
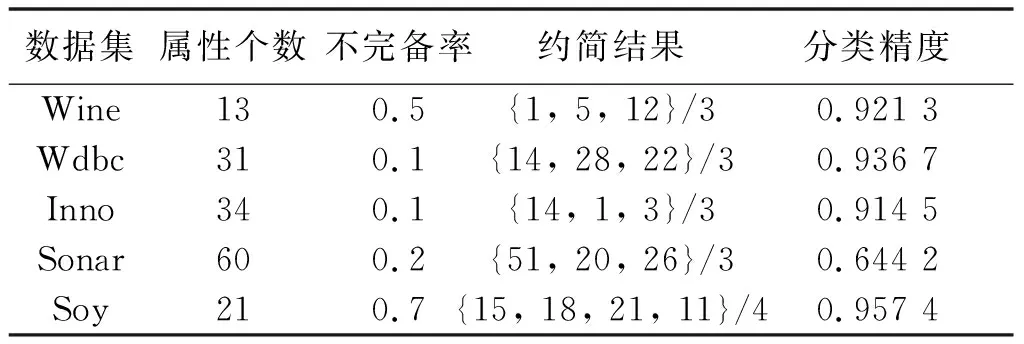
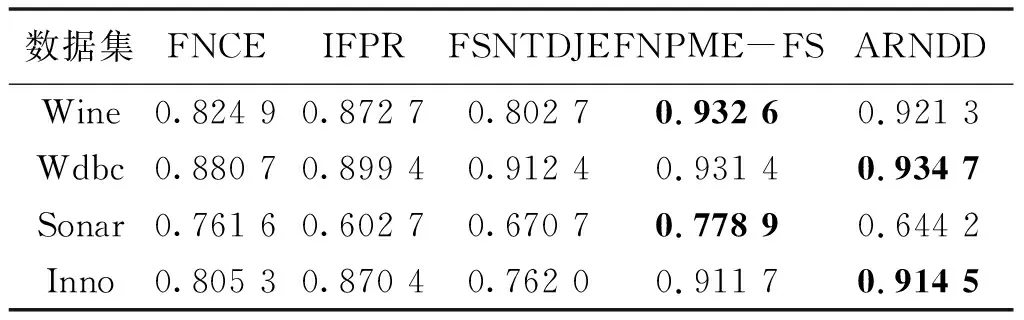
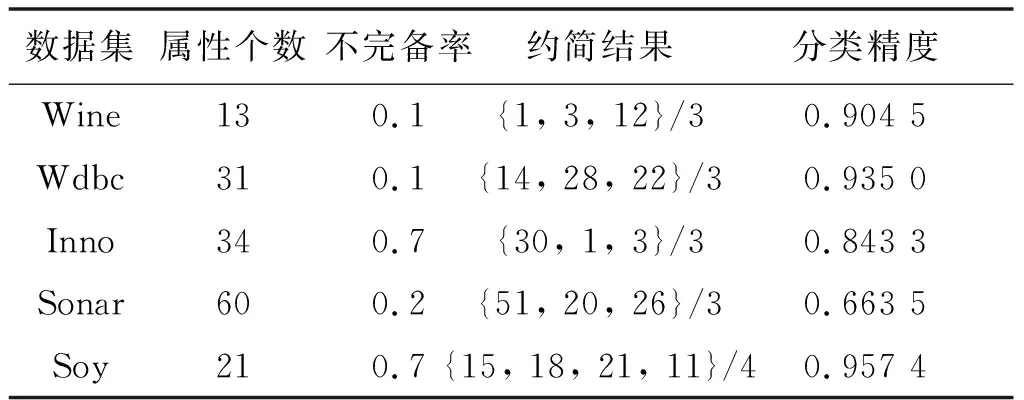
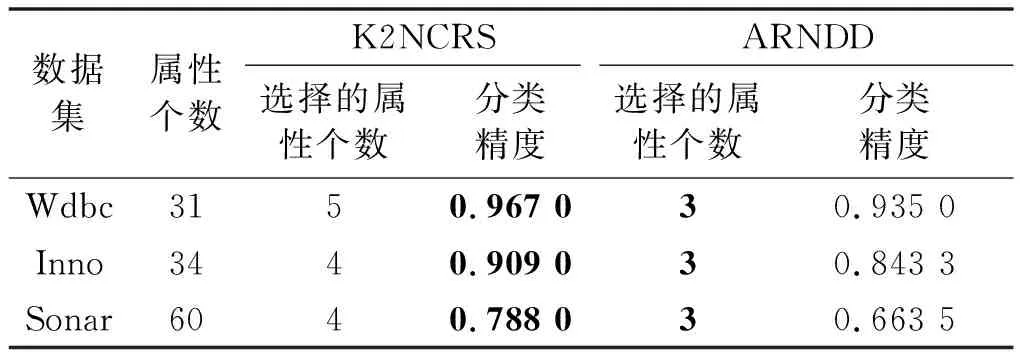
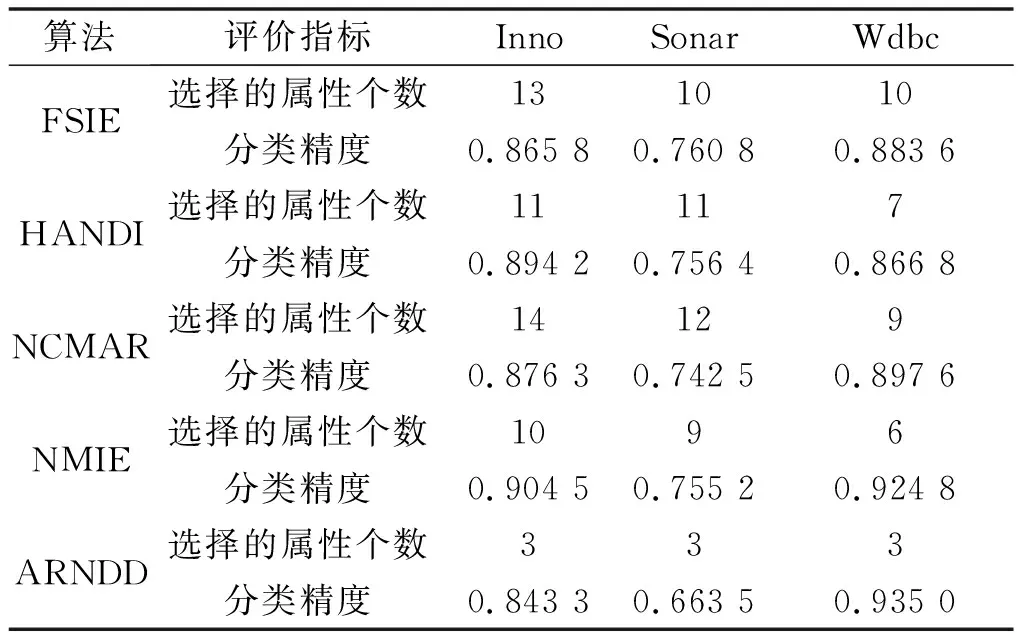
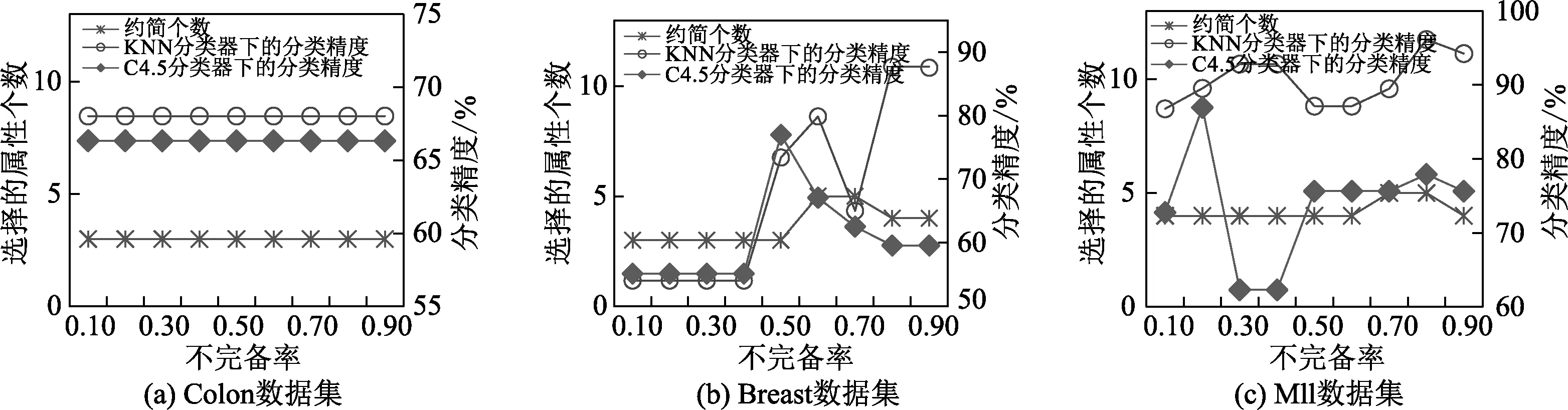
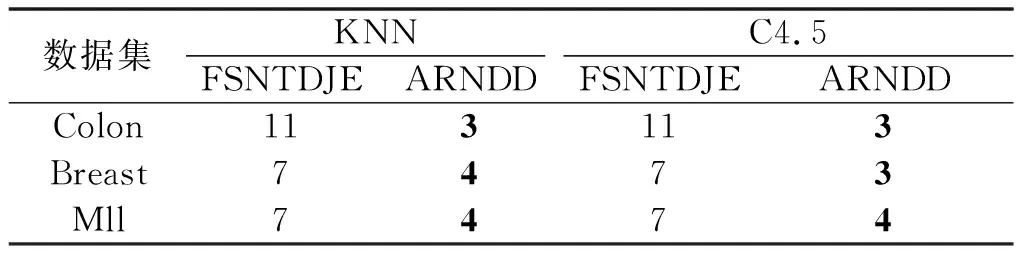
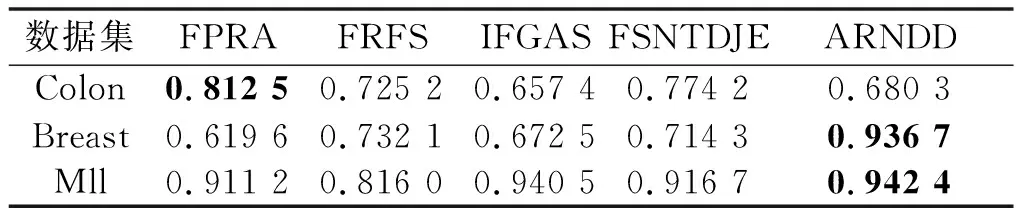
NDDC(D)

(13)

定义9在IMNDS=中，a∈B⊆C，那么a相对于D的内部属性重要度为：

Siginner(a,B,D)=NDDB(D)-NDDB-{a}(D)

(14)

定义10在IMNDS= 中，B⊆C且存在a∈C-B，那么a相对于D的外部属性重要度为：

Sigouter(a,C,D)=NDDR∪{a}(D)-NDDR(D)

(15)

定义11在IMNDS=中，B⊆C，a∈B，如果Sigouter(a,B,D)>0，那么a是B相对于D的一个核属性，且为必要属性；否则a为不必要属性.如果B中每一个属性a都为必要属性，那么属性子集B是独立的；否则B是不独立的.

文中采用前向贪心式搜索方法，设计基于邻域区分度的属性约简算法(attribute reduction algorithm based on neighborhood discernibility degree, ARNDD)，伪代码描述如下：

算法1 ARNDD算法输入:不完备混合邻域决策系统IMNDS=,给定邻域半径δ和距离函数Δ;输出:属性约简集B.Step1:初始化属性约简集B=Ø;Step2:对于任意xi∈U和a∈C,得到xi的决策类[xi]D;Step3:根据式(6)计算ΔB(f(a,xi),f(a,xj))㘷δ,得到xi的邻域容差类NTδB(xi);Step4:对于属性a计算出任意样本xi的|NTBδ(xi)∩[xi]D|,并对其结果求和;Step5:根据式(12)计算决策属性D关于a的相对邻域区分度NDD{a}(D);Step6:根据式(17)计算属性a的属性重要度Sigouter(a,B,D);Step7:搜索属性重要度最大的属性,记为a';Step8:如果Sigouter(a',B,D)>0,则B=B∪{a'},并转入Step2;否则转入Step3;Step9:返回属性约简集B.

2 实验结果与分析

通过仿真实验测试与分析所提出的属性约简算法的分类性能，实验硬件环境为Win10、CPU Intel i5-6500 3.20GHz和8G RAM，软件环境为MATLAB R2016b和WEKA 3.8.使用的8个公共数据集，如表1，所有分类实验均采用十折交叉验证.后续实验结果中粗体表示最优值.

表1 数据集信息描述

2.1 邻域参数的选择

采用Fisher评分方法[13]对3个高维基因数据集进行初步降维，分别计算不同维度下的分类精度，并选择合适的维度方便进行下一步的属性约简.图1显示了3个基因数据集的分类精度与基因数量的变化趋势.依据图1结果，将Colon、Breast和Mll这3个数据集的合适的维度分别设置为50维、100维和200维.

图1 3个基因数据集的基因个数与分类精度

针对混合数据集进行归一化处理，以减少属性量纲影响[5].邻域半径参数选择的重要标准是最大限度地平衡分类精度和选择的属性个数.在不同分类器下，以0.05为间隔设置邻域参数且δ∈[0.05,1]，选择的属性个数并计算分类精度，通过评估选择出最佳邻域参数值[3].表2为在CART分类器和SVM分类器下5个UCI数据集的最佳分类结果，表3为在KNN分类器和C4.5分类器下3个基因数据集的最佳分类结果.

表2 5个UCI数据集在2个分类器下的最佳邻域参数和分类精度

表3 3个基因数据集在2个分类器下的最佳邻域参数和分类精度

2.2 低维 UCI 数据集的分类结果

(1)CART分类器上的实验结果与分析

依据表2选择的邻域半径，对每个数据集实施不同程度的随机缺失处理.图2展示了不同不完备率下分类精度和约简个数的具体变化情况.表4给出了选择的最优分类结果.

图2 CART分类器上不同不完备率下5个UCI数据集的分类结果

表4 CART分类器上5个UCI数据集的不完备率与分类结果

根据表4可知，在5个UCI数据集上，ARNDD算法的属性约简子集大小均远小于原始属性个数；在分类精度方面，除了Soy数据集，其它4个数据集上ARNDD算法均高于0.91.与文献[16]中的FNPME-FS算法进行比较，结果如表5.

表5 2种算法选择的属性个数的比较

从表5可知，在4个数据集上，ARNDD算法的约简子集个数比FNPME-FS算法少.因此，在选择的属性个数方面，ARNDD算法得到较小的属性子集，具备较好的约简性能.

将ARNDD算法与4种算法(FNCE[14]、IFPR[15]、FSNTDJE[3]和FNPME-FS[16])进行对比，结果如表6.

表6 5种属性约简算法在4个UCI数据集上的分类精度

从表6可知，在Wdbc和Inno这2个数据集上，ARNDD算法的分类精度均优于其它4种算法；在Wine数据集上，ARNDD算法优于FNCE、IFPR和FSNTDJE这3种算法；在Sonar数据集上，ARNDD算法优于IFPR和FSNTDJE算法.

(2)SVM分类器上的实验结果与分析

与CART分类器下的实验结果类似，对每个数据集进行不同程度的随机缺失处理.图3为不同不完备率下分类精度和约简的情况.表7给出了选择的最优分类结果.根据表7的结果可知，ARNDD算法的约简结果的大小均远小于原始属性个数；在分类精度方面，在4个数据集上，ARNDD算法均高于0.84.与文献[17]中的K2NCRS算法进行比较，结果如表8.

图3 SVM分类器上不同不完备率下5个UCI数据集的分类结果

表7 SVM分类器上5个UCI数据集的不完备率与分类结果

表8 2种属性约简算法在3个UCI数据集上的分类结果

根据表8可知，ARNDD算法在选择的属性个数方面具有较好的效果，并且在分类精度方面是比较接近的.将ARNDD算法与这4种算法(FSIE[18]、HANDI[19]、NCMAR[20]和NMIE[21])进行比较，结果如表9.

表9 5种属性约简算法在3个UCI数据集上的分类精度

根据表9的结果可知，在选择的属性个数方面，ARNDD算法比其它4种算法选择的属性个数都少.在分类精度方面，在Wdbc数据集上，ARNDD算法优于其他4种算法.从选择的属性个数和分类精度2个指标综合考虑，ARNDD算法的分类能力均优于其它4种算法.

根据上述实验结果，可以说明ARNDD算法对低维UCI数据集进行分类是有效的，文中算法不仅能够删除冗余属性，而且在分类精度方面也具有较好的分类效果.

2.3 高维基因数据集的分类结果

依据表2选择合适的邻域半径，对每个数据集实施不同程度的随机缺失处理.针对3个高维基因数据集，图4为不同不完备率下选择的属性个数和分类精度结果.在此基础上，表10、11分别给出了2个分类器下选择的最优分类结果.

图4 2个分类器上不同不完备率下3个基因数据集的分类结果

表10 KNN分类器上3个基因数据集的不完备率与分类结果

表11 C4.5分类器上3个基因数据集不完备率与分类结果

从表10、11可以看出，在选择的基因个数方面，在KNN和C4.5分类器上，ARNDD算法选择的基因个数均远远小于原始基因个数.在分类精度方面，在Breast和Mll数据集上，ARNDD算法的分类精度还是较好的.

与文献[3]中的FSNTDJE算法进行实验比较，结果如表12.针对这3个基因数据集，继续与FPRA[22]、FRFS[23]、FSNTDJE[3]和IFGAS[15]这5种算法进行不同指标的比较，实验结果如表13.

表12 2个分类器上2种算法在3个基因数据集上选择的基因个数

从表13可知，在Breast和Mll这2个数据集上，ARNDD算法的分类精度均高于其它4种算法；在Colon数据集上，ARNDD算法比IFGAS算法高.总之，根据高维基因数据集的分类实验结果，ARNDD算法在KNN和C4.5分类器上均能够取得了良好的分类效果.

表13 KNN分类器上5种算法的特征选择分类精度比较

3 结论

针对不完备混合邻域决策系统，提出了基于邻域区分度的属性约简方法.首先，根据不完备混合数据之间的关系定义新的距离函数，建立了邻域容差关系、邻域上下近似集，构建了不完备混合数据的邻域粗糙集模型.在此基础上，为了更加准确地度量属性集之间的依赖关系，基于邻域粗糙集定义邻域区分度、相对邻域区分度概念.最后，基于相对邻域区分度设计一种启发式的属性约简算法.8个公共数据集上的实验结果表明，所提出的属性约简算法是有效的.