高固有频率压阻加速度敏感芯片的结构与特性分析
2022-04-19杨宇新揣荣岩姜贵民
杨宇新,揣荣岩,张 冰,姜贵民,李 新,张 贺
(1.沈阳工业大学信息科学与工程学院,辽宁沈阳 110870;2.沈阳理工大学自动化与电气工程学院,辽宁沈阳 110159)
0 引言
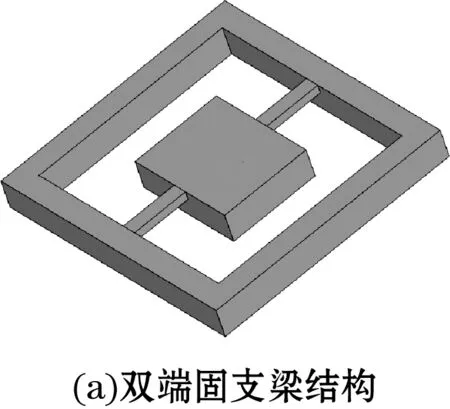
随着微机电系统(MEMS)技术的不断发展,MEMS加速度传感器的性能早已超过传统机械传感器的性能,并以其体积小、成本低、适用于批量化生产、易于集成化等优点,被广泛应用于汽车电子、消费电子、医疗、国防军工以及航空航天等许多领域[1-3]。在MEMS加速度计的各种敏感机理中,压阻传感已成为一种流行的选择[4-5]。常见的压阻式加速度传感器通常采用如图1所示的“悬臂梁-质量块”结构[6-7],其结构原型最初是由Roylance和Angell于1979年提出,具有灵敏度高、制作工艺简单以及体积小等特点[8]。经过多年的发展,这种敏感结构在设计思路和制作工艺等方面都已经很成熟,然而,它在拥有较高灵敏度的同时,固有频率低一直是限制其发展的重要因素。这是由于在普通“悬臂梁-质量块”结构中,存在着灵敏度与固有频率相互制约的矛盾[9-10],限制了MEMS加速度传感器在高端领域的应用,如在石油勘探、地震监测、微振动测量和飞机稳定性控制等应用中,通常要求加速度计同时具有高灵敏度和高固有频率[11]。所以,有必要对高固有频率加速度敏感结构进行探索和研究。
针对目前压阻式加速度敏感结构存在的弱点,本文设计了一种带有直拉直压微梁的新型压阻式加速度敏感芯片,能够在保证较高灵敏度的前提下,使固有频率提高1~2个数量级,并在提高过载能力方面表现出了明显优势,可以实现硅压阻式加速度传感器性能的综合提升。
1 结构和工作原理
所设计的带有直拉直压微梁的加速度敏感结构如图2(a)所示,主要由敏感微梁、支撑梁、质量块和硅基框架构成,Y轴为其敏感方向。该结构中,可动质量块通过4个支撑梁和4个微梁与框架相连,在每个微梁上,均设置有一个沿Y轴方向的应变电阻,并由金属引线将4个微梁上的4个电阻连接成如图2(b)所示的惠斯登电桥电路。
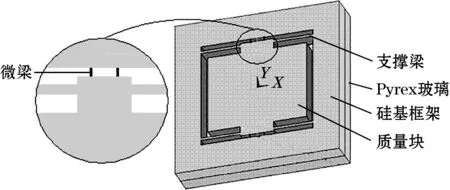
(a)结构示意图
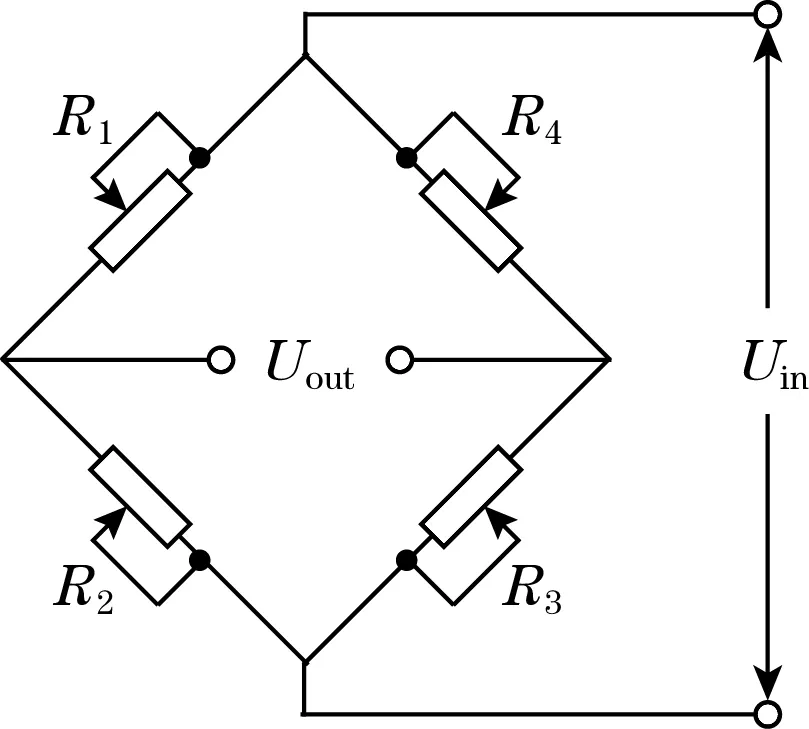
(b)惠斯登电桥电路图2 加速度敏感结构及惠斯登电桥示意图
当敏感结构受到Y轴方向的加速度作用时,由于惯性力,质量块会在Y轴方向上产生平动位移,带动微梁发生轴向变形,4根微梁中会有2根轴向拉伸,2根轴向压缩,分别产生大小相等、符号相反的正负应变,这使得微梁上的应变电阻阻值会发生相应的正负变化,由此将加速度信号转换成电压信号输出,实现加速度检测。微梁形变所引起的电阻阻值变化可表示为
(1)
式中:R为应变电阻阻值;ρ为电阻率;G1和Gt分别为电阻的纵向和横向应变因子;εl和εt分别为电阻沿纵向和横向的应变。
上述加速度敏感结构中,支撑梁的横截面积远大于微梁,因此支撑梁的刚度系数要远大于微梁,这使得支撑梁会对质量块有很强的束缚作用,微梁起的作用很小,在正常工作情况下,固有频率主要由支撑梁决定,质量块受加速度影响产生的位移极其微小,从而结构具有较高的固有频率;而微梁的横截面积较小,质量块惯性运动所产生的微小位移就会引起微梁相对显著的轴向变形,使得绝大部分应变较均匀地分布在4根微梁中,几乎所有的应力变化都能贡献给压阻检测,这就保证了灵敏度性能。因此,与传统的“悬臂梁-质量块”结构相比,该结构可以有效缓解固有频率与灵敏度之间的矛盾。
2 特性分析与讨论
2.1 输出特性
对于图2(a)所示的加速度敏感结构,利用有限元分析的方法可以仿真出其在受到加速度作用时,微梁处于拉伸和压缩状态下产生的形变,从而得到微梁上的应变分布。为了保证传感器具有良好的线性响应,需要保持微梁上应变电阻的最大应变在线性弹性范围内,单晶硅电阻的最大应变一般设计为500 με[12]。以量程50g(g=9.8 m/s2)的加速度敏感芯片为例,通过仿真得到满量程时微梁上的应变分布如图3所示,所使用的材料为单晶硅,结构参数如表1所示。
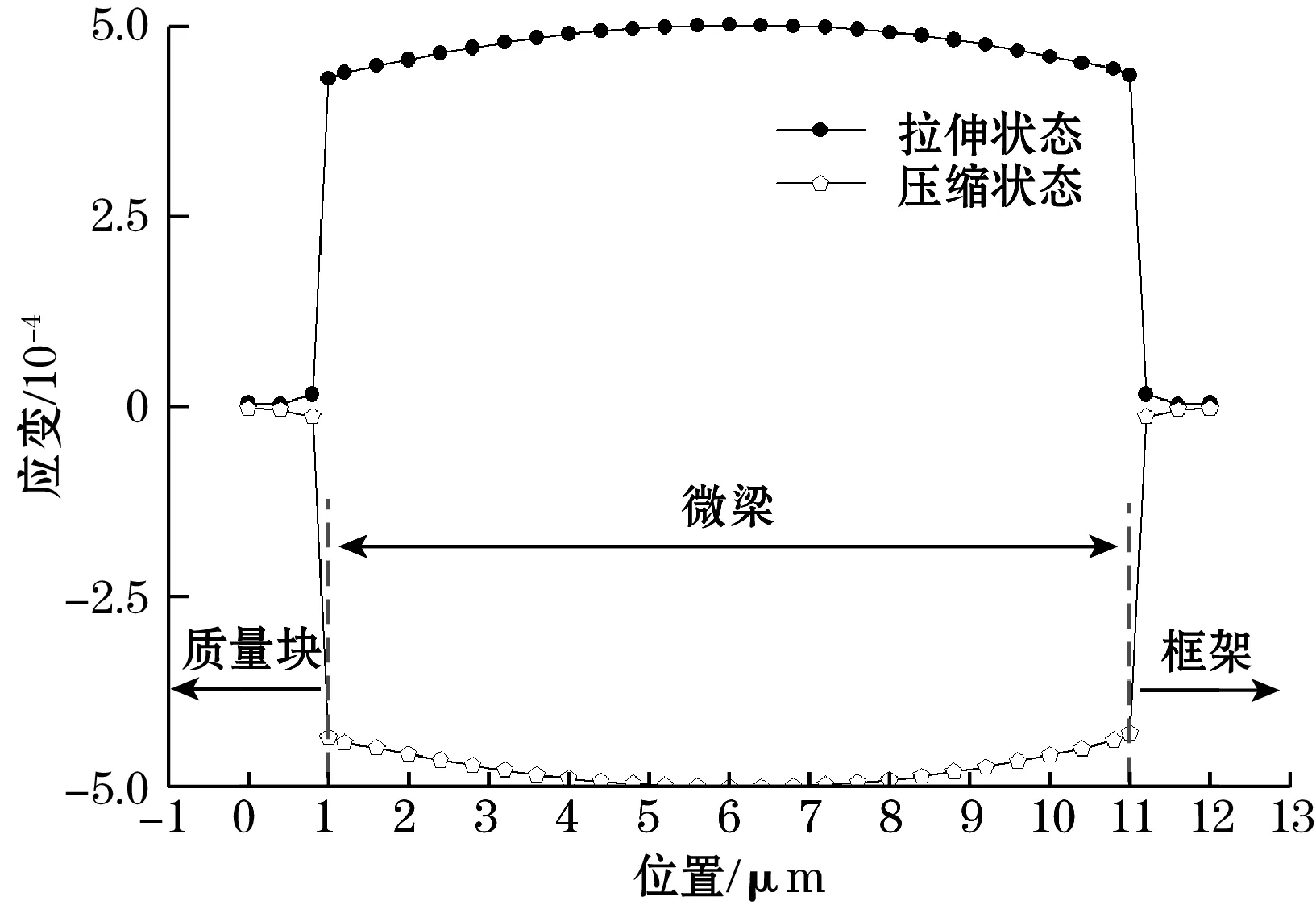
图3 微梁上的应变分布

表1 结构参数 μm
按图2(b)中惠斯登电桥电路的连接方式,传感器芯片的输出电压Uout可以表示为
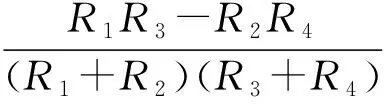
(2)
在无加速度作用的静态时,R1=R2=R3=R4=R,加速度敏感芯片的输出电压Uout为0。当有Y轴方向的加速度作用在敏感结构上时,应变电阻R1和R3发生压缩,阻值减小,R1=R3=R-ΔR1;R2和R4发生拉伸,阻值增大,R2=R4=R+ΔR2,此时输出电压Uout为
(3)
由于应变电阻在微梁上均沿Y轴方向布置,且纵向应变远大于横向应变,因此纵向压阻效应起主导作用,横向压阻效应可以忽略,通过式(1)和式(3)可得到输出电压Uout为
(4)
式中:Uin为恒压源的供电电压,Uin=5 V;G1为单晶硅的纵向应变因子,其值可取为105[13];ε1与ε2分别为电阻R1和R2上的平均应变。
对于表1所示参数的加速度敏感芯片,在50g量程范围内,依次选取不同大小的加速度载荷作用在敏感芯片上,对微梁上的应变进行仿真分析,然后利用式(4)计算出其相应的输出电压,得到芯片的输出特性如图4所示。
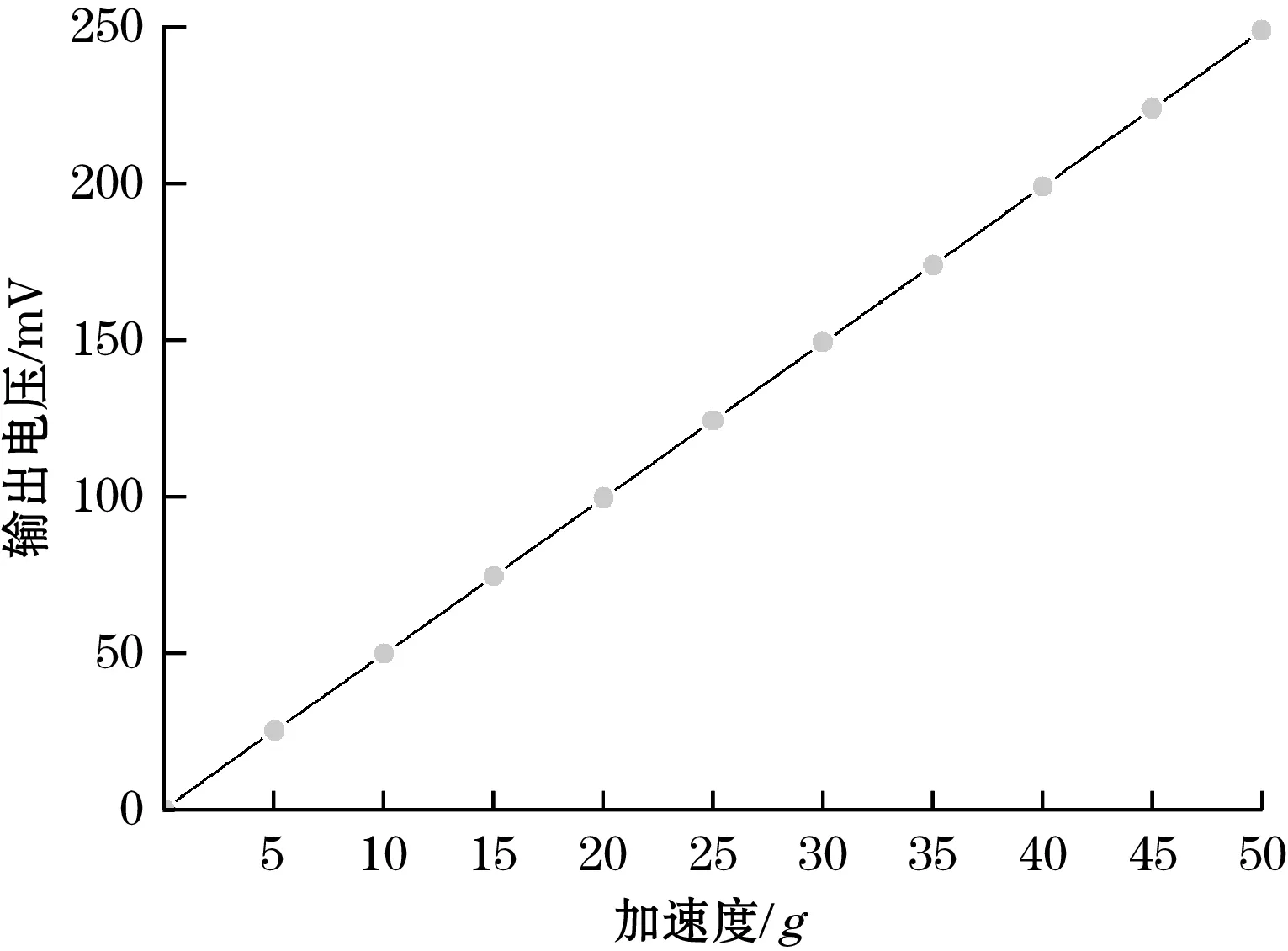
图4 加速度敏感芯片输出电压与输入加速度的关系
由图4可得,在5 V恒压源供电条件下,该加速度敏感芯片的满量程输出达到约249.4 mV,灵敏度为0.998 mV/(g·V)。基于最小二乘法线性拟合方程,可计算出其非线性度约为0.07%,敏感结构在具有较高灵敏度的同时,可以保证良好的线性输出。
2.2 固有频率
为研究本文所提出结构的固有振动特性,利用有限元的方法对表1所示参数的加速度敏感结构进行了模态分析,同时,在保持量程和灵敏度与表1中的加速度敏感芯片基本一致的前提下,通过仿真分析得到图1中的双端固支梁结构以及四端固支梁结构的模态频率,3种加速度敏感结构的前五阶模态频率如表2所示,其中一阶模态为工作模态,所对应的频率即固有频率。
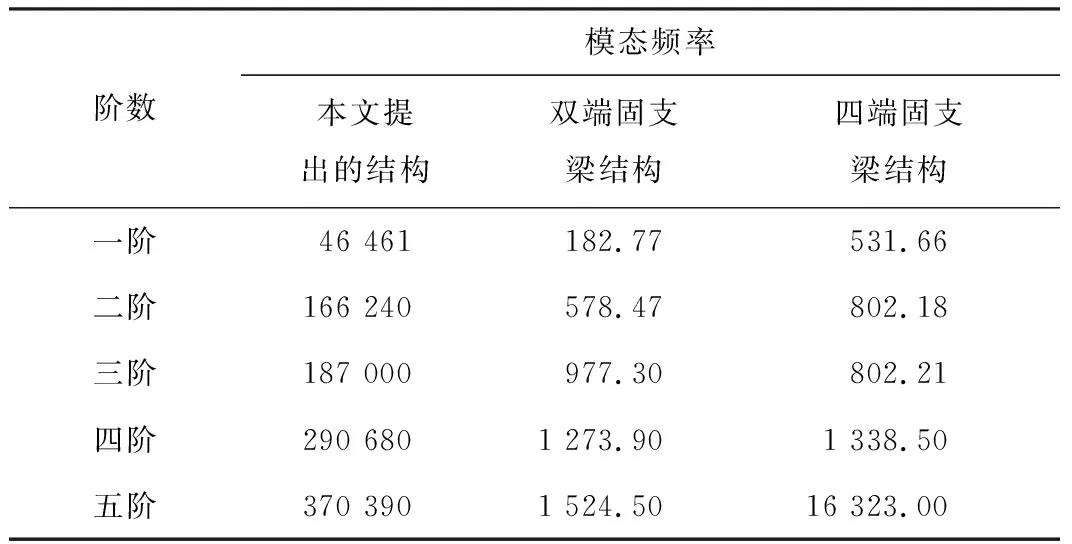
表2 3种加速度敏感结构的前5阶模态频率 Hz
从表2可以看出,对于双端固支梁结构和四端固支梁结构,其固有频率分别为182.77 Hz和531.66 Hz,而本文所提出结构的固有频率达到了46 461 Hz,且一阶模态频率与二阶和三阶模态频率均相差很大,这说明其交叉耦合很小。通过对比3种加速度敏感结构可知,在保证灵敏度基本相同的前提下,本文提出的结构显著提高了固有频率,其固有频率可达四端固支梁结构固有频率的87倍以上,而相比于双端固支梁结构,固有频率约为其254倍。
表3列出了文献[11、14、15]中的结构以及7270型商用压阻式加速度传感器的灵敏度与固有频率参数,并使用两者的乘积值作为衡量传感器性能的指标,将这4种结构与本文提出的带有直拉直压微梁的加速度敏感结构进行了对比。通过表3可知,与这些改进的新型结构以及商用传感器相比,本文提出的结构在灵敏度和固有频率综合性能方面表现出了明显优势。如表3中的双岛五梁加速度敏感结构[15],其固有频率为4.9 kHz,灵敏度为0.15 mV/(g·V),而本文提出结构的灵敏度为0.998 mV/(g·V),固有频率达到46.461 kHz,相比之下,灵敏度与固有频率的乘积值达到前者的63倍。
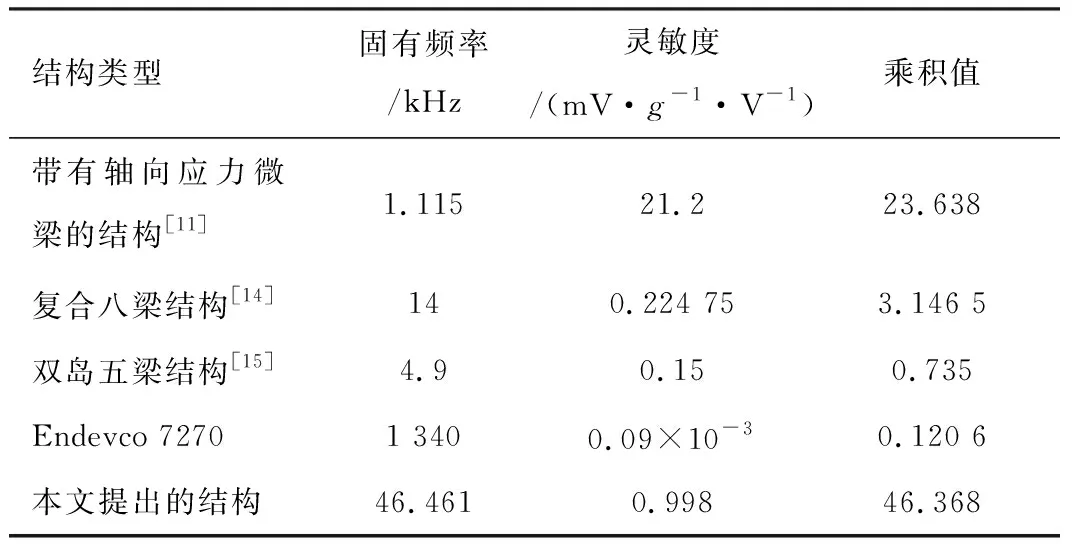
表3 不同类型加速度敏感结构的性能参数
2.3 过载能力
对于图2(a)所示的加速度敏感结构,当其受到高g值的冲击加速度作用时,若支撑梁或者微梁上的最大应力超过单晶硅的抗拉强度,梁就会发生断裂,从而导致传感器失效。单晶硅材料的抗拉强度具有尺寸效应[16-17],即材料的抗拉强度随试件几何尺寸变化而变化的现象,所以不同尺寸的梁会表现出不同的抗拉强度,这将对敏感结构的过载能力产生很大影响。因此分析敏感结构的过载能力,首先需要给出结构尺寸与抗拉强度的关系。
上述加速度敏感结构中,支撑梁及微梁的长度和宽度均远大于其各自的厚度,所以梁的抗拉强度主要受厚度的影响。参照文献[16]的实验结果,得到厚度分别为1.91 μm、19 μm和520 μm单晶硅材料的抗拉强度平均值,如表4所示;根据文献[17]的实验结果,计算得到50 μm厚度单晶硅薄膜抗拉强度的平均值,结果如表4所示。

表4 不同厚度单晶硅材料的抗拉强度值
通过分析表4数据,并对其进行函数拟合,求得单晶硅薄膜的抗拉强度随厚度的增加成指数规律衰减,最佳拟合函数关系式为
y=a·e-bx+c
(5)
式中:x为单晶硅薄膜厚度;y为相应的抗拉强度。
求得a=7.736 26,b=0.042 44,c=0.474 7,并绘制出单晶硅薄膜抗拉强度与厚度之间关系曲线如图5所示。
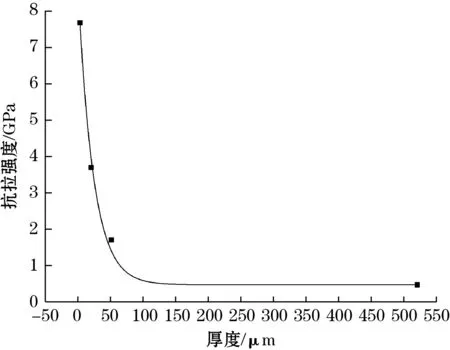
图5 单晶硅薄膜抗拉强度与厚度之间的关系
对于表1所示的量程为50g的加速度敏感芯片,其支撑梁厚度为50 μm,微梁厚度为0.3 μm,根据表4和式(5),可得到支撑梁和微梁相应的抗拉强度值分别约为1.7 GPa和8.1 GPa。通过仿真得到,当在敏感芯片上施加1 180g加速度时,微梁上的最大应力达到0.3 μm厚度所对应的抗拉强度值,而此时支撑梁上最大应力仅为6.4 MPa,远远低于1.7 GPa。因此,该芯片的过载能力约为1 180g,达到满量程的23.6倍。
若不采用任何提高过载能力的措施,并将满量程最大应变设计为500 με,通过仿真可知无论是双端固支梁结构还是四端固支梁结构,其自身的过载能力均为满量程的3倍左右。而本文所述结构与其相比,在无过载保护的情况下,过载能力可达到23.6倍量程,提高了6倍以上。
2.4 交叉耦合
对于MEMS加速度传感器来说,交叉耦合系数是一项比较关键的性能参数,对其测量精度有着直接影响,在应用中一般要求交叉耦合系数不超过5%[18]。交叉耦合产生的原因主要是:当芯片受到非工作方向的加速度作用时,结构因受到惯性力作用也同样会产生变形,致使桥臂电阻发生变化,电桥产生电压输出,从而引起交叉耦合,影响敏感方向上信号的测量精度。
对于表1所示的量程为50g的加速度敏感芯片,Y轴为其敏感方向,X轴和Z轴为非工作方向。当在敏感芯片的X轴和Z轴方向分别施加加速度载荷时,利用仿真可分析出微梁上的应变,从而计算得到不同大小的加速度作用在非工作方向时的输出电压,如图6所示。通过分析图6的数据可知,该敏感结构具有非常低的交叉灵敏度,对工作方向上加速度检测的干扰非常小,计算可得其交叉耦合系数约为0.1%。
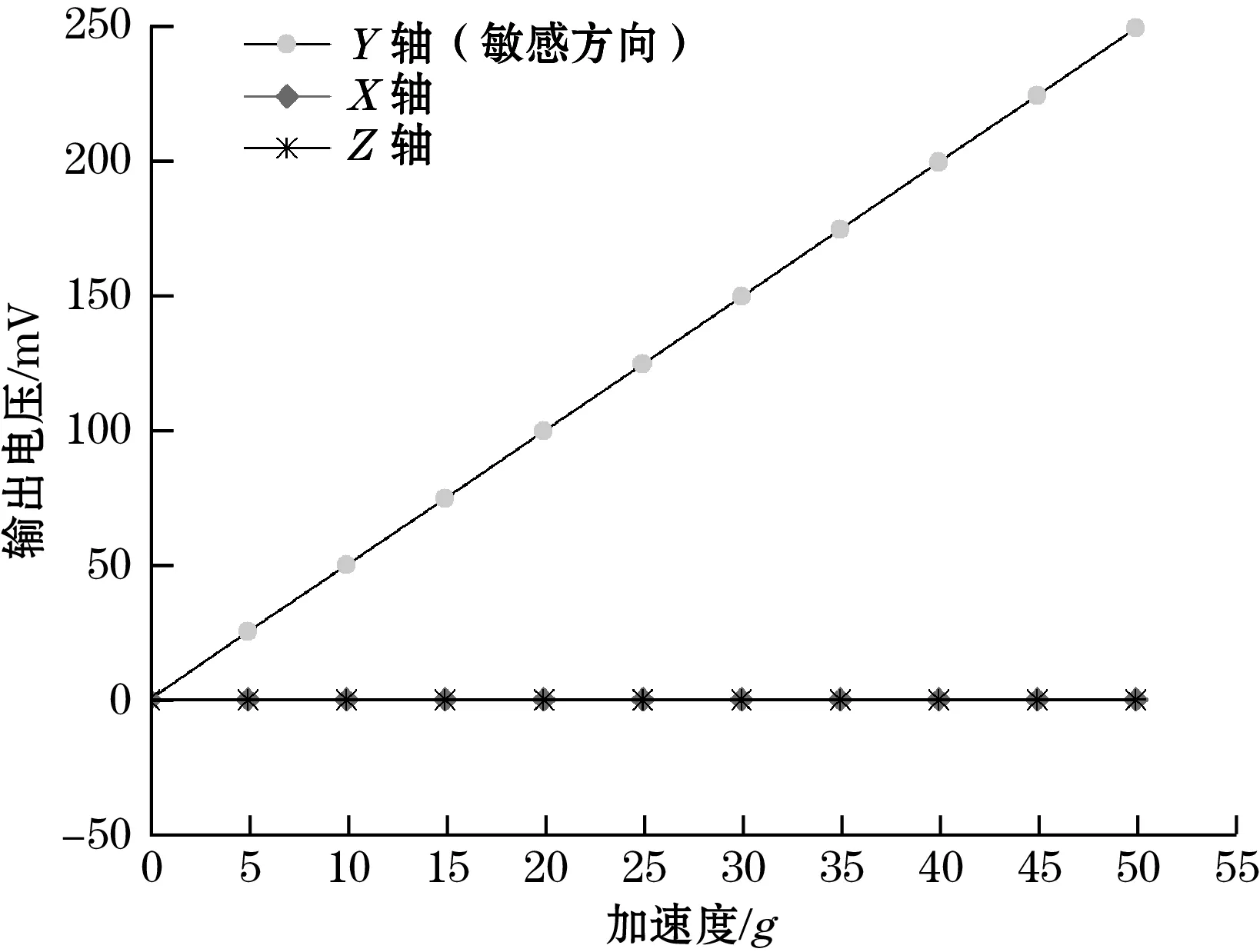
图6 敏感结构受到不同方向加速度作用时的输出电压
3 结论
本文构建了一种带有直拉直压微梁的压阻式加速度敏感结构,利用有限元法对该敏感结构的性能进行了仿真分析,结果表明,在保证较高灵敏度及良好线性输出的前提下,其固有频率达到普通“悬臂梁-质量块”结构的87倍以上,使得灵敏度与固有频率之间相互制约的矛盾得到有效缓解,同时和普通MEMS加速度敏感结构相比,过载能力可提升6倍以上,并具有非常低的交叉灵敏度,交叉耦合系数可控制在0.1%左右。
