超声焊接圆锥复合变幅杆的设计与分析

李永亮，王敬* , ，马毓

（1.重庆工商大学 机械工程学院，重庆 400069；2.重庆工商大学 制造装备机构设计与控制重庆市重点实验室，重庆 400069）

超声变幅杆是实现换能器到负载之间的聚能、振幅放大、阻抗匹配的关键部件，在超声塑料焊接领域应用广泛[1]。因加工领域、加工对象不同、材料不同，变幅杆形式多种多样，缺乏面向工程应用的、统一的、高效的设计、试验方法，在实际工程应用中是一个难点。随着大功率超声器件在工业领域的广泛应用，国内外学者对各种类型的超声变幅杆进行了大量的理论分析和试验研究。国外学者从上世纪四五十年代起就开展了超声加工的研究，近年来，在复合超声变幅杆的设计、有限元分析、加工热弹性响应、优化设计、试验分析、疲劳分析、受载安全评估等方面进行了大量的研究[2-7]，研究领域渗透到超声振动切削技术，超声复合加工技术硬脆复合材料高精密加工等技术领域[8~10]。国内学者林中茂[11]研究了超声变幅杆的原理和设计方法；潘巧生等[12]进行了一种等应力大振幅变幅杆的设计并进行了有限元分析；李新和等[13]进行了超声旋压系统的变幅杆的设计和有限元仿真，并得出有限元仿真与试验分析的吻合性；闫晓东等[14]研究了纵扭复合超声换能器的设计与仿真；刘湘晨等[15]基于CAD/CAE的一体化分析方法，对变幅杆的设计进行了程序化的设计，简化了计算和绘图，提高了设计效率，仿真比较理想；马继召等[16]通过UG的二次开发功能，应用VC++编程，实现了变幅杆的参数化三维设计。此外，国内其他学者也针对阶梯形变幅杆有限元分析、纵振特性等性能进行了研究分析[17-18]。针对变幅杆的设计，有限元的设计方法和仿真分析已成为技术的主流，然而，随着应用领域的拓宽，复合变幅杆、异形变幅杆的需求日益增多，因此，研究用于带异形工具头的复合变幅杆的高效设计、仿真分析、试验研究的通用方法在工程实践应用中就显得尤为重要。

基于此，利用圆锥形复合超声变幅杆的参数化设计与工具头结构优化的设计思路，围绕有限元仿真分析与阻抗测试分析，探索出单头复合变幅杆的振型、共振频率、阻抗分析方法，设计了用于超声塑料焊接系统的半波长圆锥形复合变幅杆。

1 纵波复合变幅杆的参数化设计

1.1 设计基础资料

设计内容来源于一款耳机外罩防尘钢网超声焊接的工程项目，设计需求是将防尘钢网及防尘薄膜焊接至耳机外罩上，设计特点上防尘钢网尺寸较小，耳机焊接孔避空尺寸较小，焊接深度较浅，需求高频率，低振幅就可以完成焊接过程，因此超声焊接可选用40 kHz的频率发生器及与之配套的超声换能器，耳机防尘钢网焊接工作需求图及超声频率发生器、超声换能器如图1所示。

图1 耳机防尘钢网焊接要求图

超声焊接需要实现将频率发生器发出的电能经由超声换能器转变成振动机械能，然后经过超声变幅杆聚能、振幅放大完成焊接过程。超声变幅杆的材料选择上有很多种，诸如钢类材料，40钢、45钢、20Cr、12CrNi3A、30CrMnSiA 等；钛合金类，如BT-1、BT-4、OT-4等；铝、镁合金材料等。钢材损耗较大，往往需要热处理，工艺复杂，钛合金性能最好，但价格较高，机械加工难度较大，因此，针对加工特点，本设计变幅杆材料选择铝合金，且选择铝合金性能强度最好的，加工性能优的，耐磨性较好的7075铝合金，材料主要属性及变幅杆主要参数如表1所示。

表1 7075 铝合金材料性能参数表

根据均匀细棒的纵向振动原理，定义细棒轴向为x轴，截面积为S，在动态应力的作用下产生纵向位移，在x处的应力为，取微元， 根据牛顿第二定律可知波动运动方程为

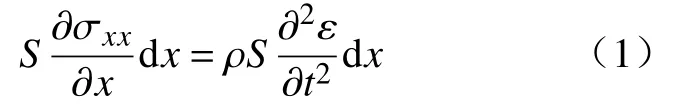
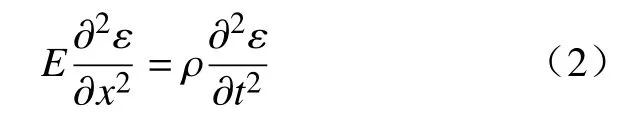
式中：E为杨氏模量；ρ为棒材的密度。

纵波在棒体传输速度公式为

由于棒是有界的，声波在端面上会产生反射，形成正向和反向波的叠加，因此可通过对式（2）取解，并通过两端自由的纵波传输和两端固定的纵波传输的边界条件从而可求解纵波传输的波动方程，并进一步确定自由纵振条件下的固有频率值。声波在均匀固体棒材介质中做纵波传输的波长为

变幅杆为纵波传输，为计算方便，取半波长圆杆作为变幅杆主要尺寸及外形。变幅杆的大端直径D不小于超声换能器辐射面的线度，因此D取25 mm；小端直径d一般按照加工对象来取，耳机防尘钢网直径约3.5 mm，为计算方便，避免过大的放大系数，d取5 mm。在计算完成后，再优化结构为3.5 mm的焊接工作D（25 mm）应小于波长的四分之一（31.415 mm），因此能够满足纵波传输条件。具体变幅杆参数如表2所示。

表2 变幅杆参数表

1.2 纵波传输复合变幅杆波动理论

工程上单一变幅杆的形状及外形多种多样，为求解方便，往往需要设计一些跟随纵向坐标有规律变化的函数型外形变幅杆，以便得到波动方程的解，较多的是指数形、悬链线形、圆锥形、阶梯形等，然而为了兼顾形状因数、放大系数，尤其是在高速振动时，常常也用复合形变变幅杆。基于变幅杆的参数表的选择，为了便于数控车削加工，变幅杆采用了带圆锥形过渡的复合变幅杆，截面尺寸为圆形截面。图2为半波长复合圆锥变幅杆波形传动图。

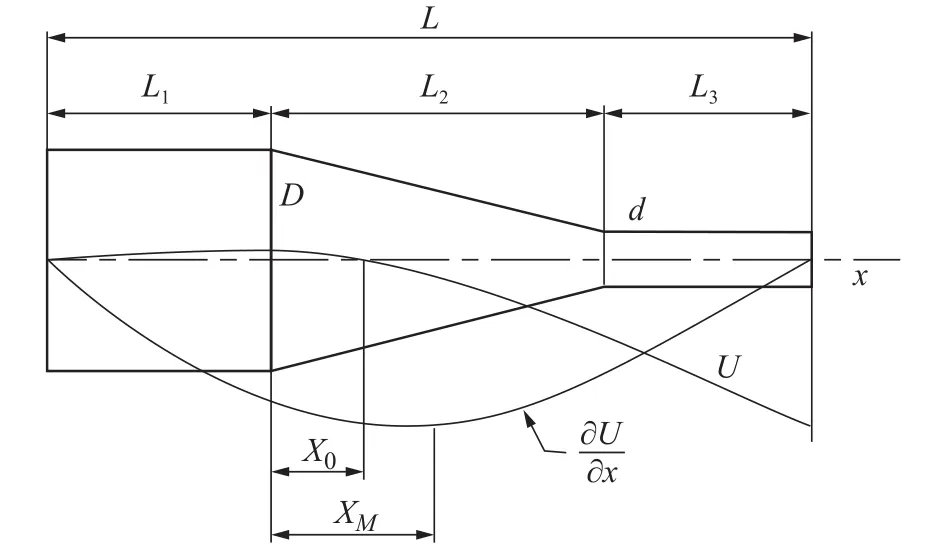
图2 半波长复合圆锥变幅杆波形传动图

结合波动理论，根据图2可知面积系数N为

圆锥形曲线坐标方程为

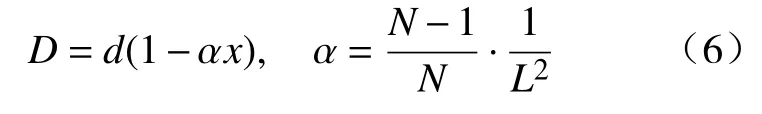
为计算方便通常可取L1=L3，即KL1=KL3=0.1π+0.025π×n(n=0,1,...)，将两端自由状态的复合变幅杆的边界条件代入波动方程（2）中，可以求得带圆锥过渡形状的复合变幅杆频率方程，即

当KL2≤ π时，取“+”；KL2>π时，取“–”。

以半波谐振长度为计算，取KL1=0.225π，则有

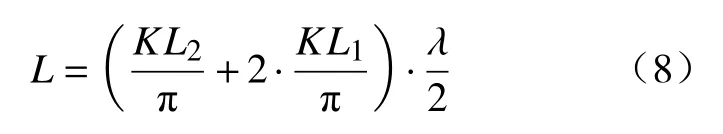
可分别求得L1=L3=14.14mm，L2=56.18mm，L=84.46mm，记H=KL2/π，H=0.894。

1.3 三维参数化建模设计

工程实践应用中，将选择好的变幅杆材料参数（表1）和变幅杆参数（表2）以固定参数嵌入三维设计建模软件Solidworks中，在零件建模环境中，选择上视图作为草图环境，绘制变幅杆截面图形，并对截面图形进行回转特征建模。建模后，在模型树中，将需要的变量参数输入到方程式的工具菜单中，输入变量如图3所示，变量的设置可以根据自己的需要添加或者删减，主要设计的变量参数为大端尺寸D，面积系数N，变幅杆传输波长λ，半波谐振长度系数KL，谐振长度变换系数H等。

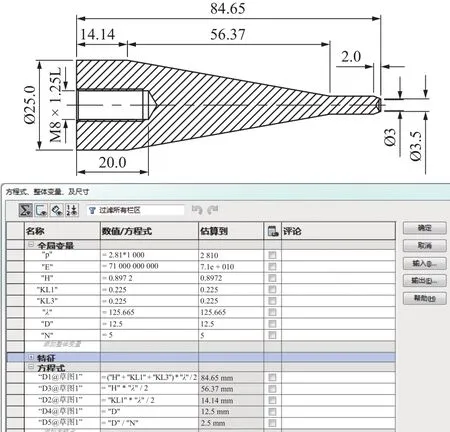
图3 变幅杆参数化建模图

在显示的特征尺寸中嵌入变量参数方程式，便于三维建模，同样在后续的变幅杆建模、谐振频率仿真调整等过程中均可对某些变量进行参数化设计，便于快速修改尺寸。此外，在后续其它的变幅杆设计中，尤其同样是半波长的圆锥变幅杆，只需改变相关参数就可以快速实现参数化建模。

2 有限元模态分析与优化

2.1 模态分析

有限元模态分析是进行结构的固有频率、振型与振型参与系数的一种线性分析方法。有限元模态分析方法已被广泛应用于变幅杆的设计、仿真中，并且被证实能够在频率分析，应力应变位置分析以及预测疲劳断裂位置及寿命有很好的指导意义。在有限元分析中，通常假定变幅杆为横截面积大小固定，材料密度和弹性常数均匀且没有机械损耗的弹性体，该弹性体做无阻尼的自由运动，根据有限元分析中系统动力学方程和线性系统中的自由振动运动方程，可以得到振动频率 ωi和模态 φi的关系方程为

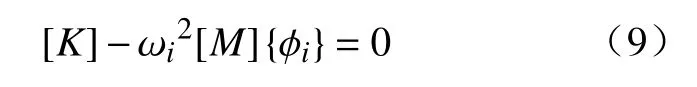
应用Ansys Workbench工具箱中的Modal进行分析，具体步骤如下：

1）导入“.X_T”三维模型文件；

2）设置材料属性，需注意的是新建一个材料属性，需添加7075铝合金材料属性；

3）定义网格，网格划分可采用自动划分方式，网格大小设为5 mm；

4）在Analysis Settings的属性窗口中设置提取的模态阶数为6阶，设计提取的频率变化范围为38～42 kHz，由于超声振动模态分析进行的无约束的自由模态分析，因此不添加载荷和约束；

5）进行求解，可以发现在设置的频率范围内的6阶求解结果只有一个共振固有频率即39502.0 Hz，且振动形式为纵波传输，从整体变形方式上看，端头的变形最大，符合工具头的设计，模态分析如图4所示。

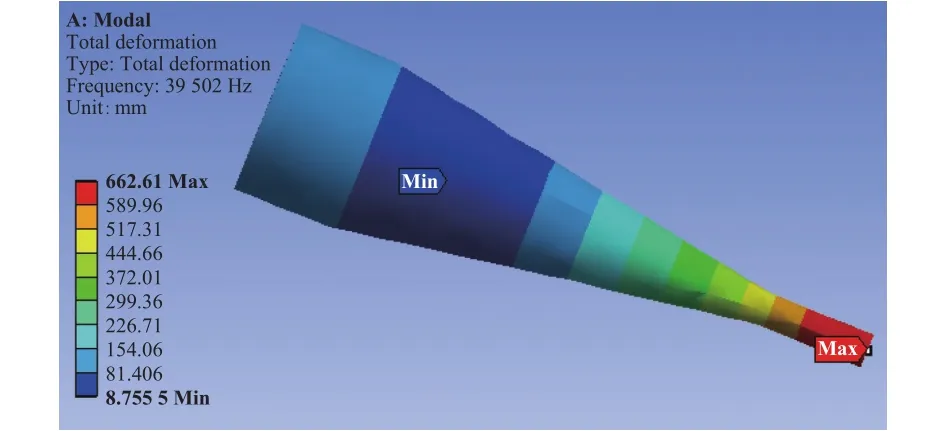
图4 变幅杆优化前模态分析结果图

2.2 变幅杆结构优化

结合设计要求，变幅杆需进行结构优化，主要体现在以下位置：1）变幅杆与超声换能器的连接采用螺纹连接方式；2）结合耳机罩防尘钢网焊接孔的焊接要求，经测量，变幅杆的端头需要设计Ø3.5 mm的直径，且中间打个锥形孔的工具模头，便于焊接；3）需对耳机Ø3.5 mm直径的工具头进行倒圆锥角处理防止端头应力过度集中，导致焊接工具头内部组织断裂失效；4）对大端直径铣削两条直角边，便于用扳手将变幅杆与换能器连接紧固，结构优化如图所示图5所示。应用同样的方法对结构优化后的变幅杆进行有限元模态分析，得到的固有频率图及振动矢量图分别如图6和图7所示。

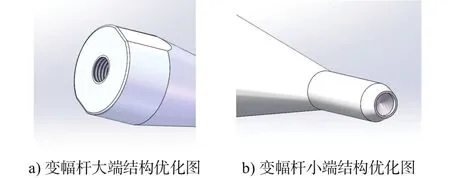
图5 变幅杆结构优化图

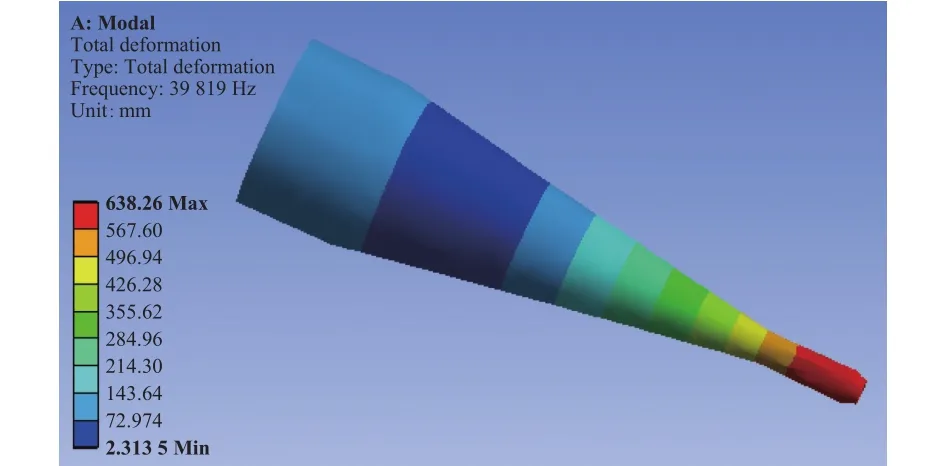
图6 优化后变幅杆模态分析结果图

图7 优化后变幅杆模态分析振动矢量云图

从结构优化后的变幅杆模态分析结果来看，优化后的变幅杆固有频率为39819.0 Hz，较优化前的固有频率 39502.0 Hz，提升了 0.802%，与设定计算的40000 Hz 的频率，误差为 0.45%，偏差较小。此外，根据超声频率发生器能够匹配的频率信号为39800 ～40200 Hz，当前的变幅杆模态仿真频率满足此频率范围，说明在有限元仿真条件下，变幅杆的振型及固有频率设计满足要求。总体来看，经结构优化后的变幅杆，整体频率变化不大，且振动形式仍为纵振，振动的最大变形方向仍然集中在小端的焊接工具头上，说明通过参数化纵振波动传输频率方程计算后的变幅杆，在有限元模态分析设定较宽频率范围内只存在一个与设计频率比较接近的固有频率，且局部小尺寸的结构优化对于整体变幅杆振型及频率的影响不大，即便增加求解阶数，也不会对固有频率产生极大的变化，极大了避免了因变幅杆结构变化产生的弯曲、扭转等波动形式对变幅杆设计的影响。

3 谐响应分析与试验分析

3.1 有限元谐响应分析

变幅杆的理论计算和有限元模态分析往往都是基于空载条件下进行的，然而实际应用中，变幅杆的输出端面都是有负载的，比如超声乳化、超声焊接、超声成型等应用中，而且超声的负载有可能随着加工工具的不同而不同，比如超声焊接中，随着焊接工具与焊接件接触到熔化的过程，负载都是不断的变化的，理论计算时，往往可以将负载等效为质量的抗性负载进行计算，然而计算过程复杂，工程实践应用性不强，为此，采用有限元的谐响应分析为变幅杆有负载情况下的简谐频率及变形分析提供了技术支撑。应用Ansys Workbench工具箱中的Harmonic Response模块进行分析，在自由谐振条件下，对端头锥形工具头进行加载，加载的静压力按气动控制系统进行估算，气缸静压力估算值为100 N，设定谐响应分析的频率范围为超声波频率发生器的电信号采集频率，频率值在 39800～40200 Hz 范围内，进行求解，计算的总变形量（Total deformation）响应结果图如图8所示，计算的最大弹性应变图如图9所示，计算的频率变形响应图如图10所示。

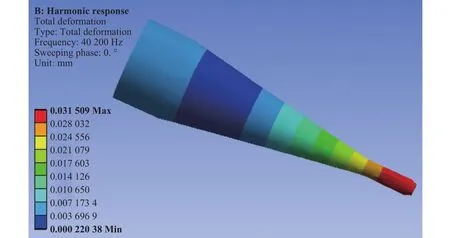
图8 总变形量谐响应分析图

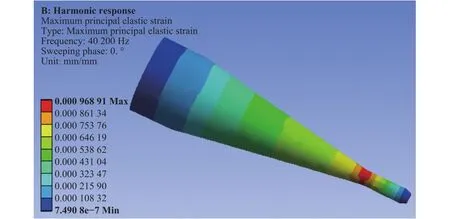
图9 最大弹性应变谐响应分析图

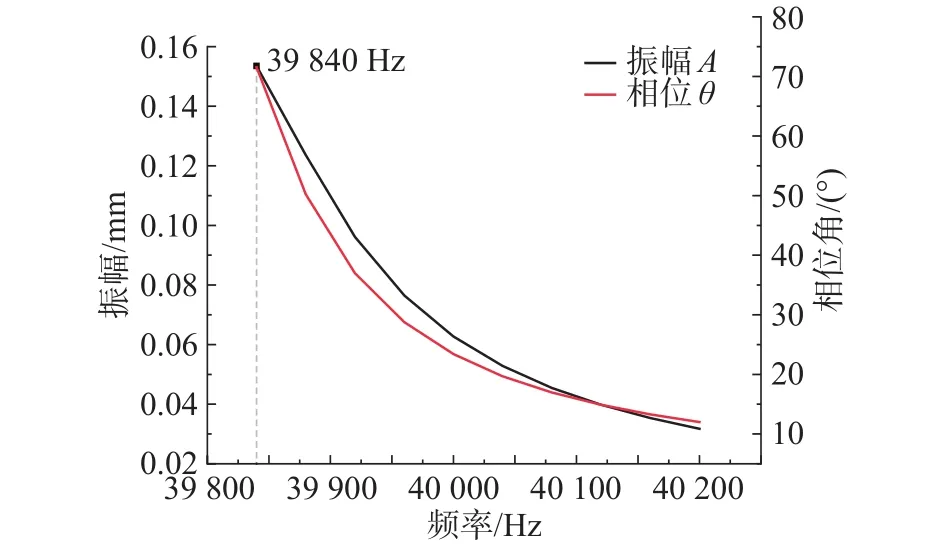
图10 频率谐响应分析图

从图8可以看出，变幅杆在加载状态的总体最大变形量主要集中在变幅杆的前端工具头上，最大数值为31.509 μm，能够满足塑料与金属防尘网格的超声焊接要求。从图9可以看出，加载状态的变幅杆，最大主弹性应变主要集中在圆锥形与小端圆柱形的连接处，数值为 0.9689 μm，说明此处存在较大的应变，在长期的高频振动状态下，可能会产生组织疲劳断裂，从而影响变幅杆的使用寿命，在后期的研究中可进行疲劳寿命试验分析。从图10可以看出，加载状态的变幅杆，随着输入频率的变化，变幅杆的振幅及相位均呈现单调递减状态，且在39840 Hz时有最大的振幅，即此处为加载状态的最大共振频率。

3.2 阻抗与试验分析

为了验证变幅杆理论设计及仿真的可靠性与合理性，应用数控技术进行变幅杆加工，并应用阻抗分析仪分别对超声换能器和变幅杆进行频率、阻抗分析，测试图如图11和图12所示。

图11 超声换能器阻抗分析图

图12 超声换能器及变幅杆阻抗分析图

从阻抗分析可以看出，对超声换能器单独测量时，阻抗分析仪采集共振频率为 39920 kHz，对超声换能器和变幅杆一体测量时，阻抗分析仪采集共振频率为39867 Hz，总体频率变化率在 0.1%以内，变化较少，如图13和图14所示，且该频率在频发发生器的发波频率39.8～40.2 kHz范围内，满足频率发生器的发波要求，从阻抗分析上来看，超声换能器的阻抗在12.4 Ω，而超声换能器和变幅杆一体测量的阻抗在43.8 Ω，按照阻抗分析仪的技术指标，阻抗值在10 ～60 Ω以内，不会引起超声波频率发生器的能量损失，能够满足超声加工要求。为此将超声加工系统安装在如图15所示的台式超声加工机床上，经加工验证设计的变幅杆能够完成耳机防尘钢网、防尘膜的焊接，且经工程实践产品检验验证，防尘钢网焊接强度在工程技术要求14 N以上，满足产品的焊接技术需求，焊接质量较好，焊接效率较高。

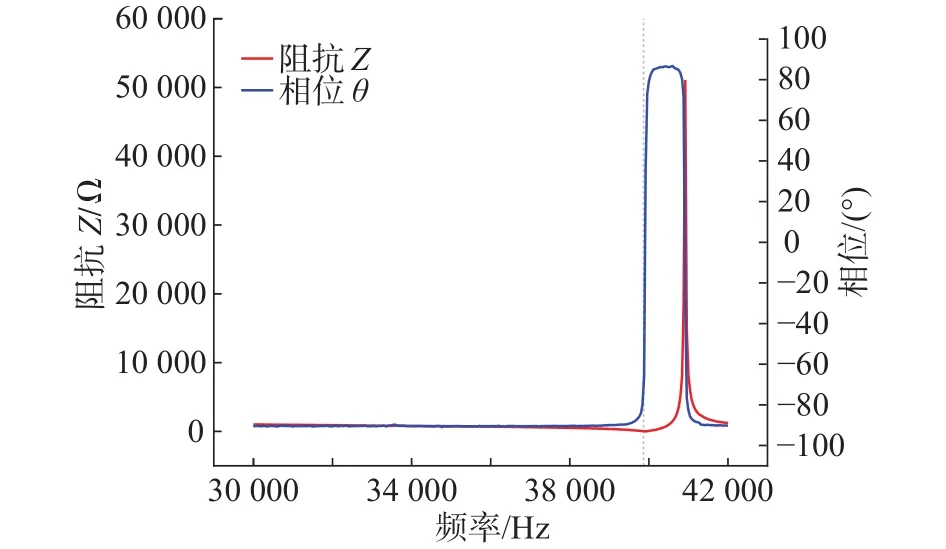
图13 超声波换能器阻抗分析图

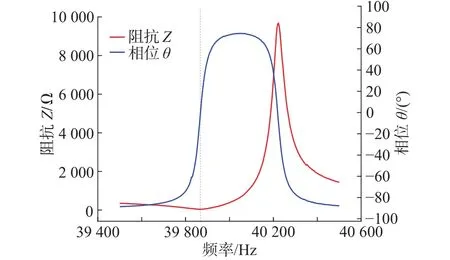
图14 超声波换能器及变幅杆阻抗分析图

图15 耳机防尘钢网超声焊接加工图

4 结论

根据超声焊接需求，基于波动理论，给出了一般复合变幅杆的主要尺寸参数公式，并将相应设计参数及公式嵌入到三维建模软件中，可以实现圆锥复合变幅杆快速结构设计及结构优化；应用Ansys Workbench 当中的 Model和 Harmonic Response模块可以对初步设计的焊接变幅杆进行振型、固有频率，加载共振频率、最大应变及总变形量等参数的仿真分析，仿真得到的共振频率为 39840 Hz，与阻抗分析仪测试的共振频率39867 Hz误差较小，解析计算、有限元分析、阻抗测试在振型与共振频率分析上吻合度较高，且在频率发生器的发波范围内，同时阻抗值为43.8 Ω，满足设计要求，加工测试验证了设计的合理性，为通用单头超声圆锥复合超声变幅杆的设计、分析提供了依据。