面向整车振动抑制的磁流变阻尼器协同优化

韦鑫鑫，朱孙科，邓召学

（重庆交通大学 机电与车辆工程学院, 重庆 400074）

近年来，智能材料研究领域的拓展吸引了众多的研究者，在现有的各种智能材料中，对磁流变液进行了大量的文献研究[1]。磁流变阻尼器作为一种半主动减震装置，以磁流变液为工作载体，具有响应速度快、阻尼连续可调、良好的电磁可控能力，在车辆和桥梁减震方面具有广泛的应用[2-3]。作为汽车半主动悬架主要的组成部分，磁流变阻尼器的设计直接关系到输出阻尼力的大小，影响悬架的隔振性能。对此许多学者进行了相关研究，对阻尼器进行优化，已成为阻尼器系统设计和开发的重要环节。

文献[4]以磁流变阻尼器阻尼力和流动间隙处磁通密度最大为优化目标，利用智能优化算法，对磁流变阻尼器结构参数进行优化，结果表明，优化后的磁流变阻尼器性能更佳。文献[5]为了获得流体流动间隙的最大磁通密度，对磁流变阻尼器进行了几何优化。优化后的磁流变阻尼器能够提供了最大的磁通密度。聂松林等[6]为了研究不同活塞结构对工作间隙磁通密度、剪切应力、粘滞应力和动态范围的影响，对磁流变阻尼器的结构参数进行优化。Nanthakumar等[7]为了改变磁流变减振器阻尼力，对活塞的尺寸和活塞内流动通道的长度进行了优化设计。胡国良等[8]为了在固定尺寸内获得磁流变阻尼器的最优阻尼性能，提出一种基于DOE及RSM的优化设计方法对其进行结构优化设计。冯志敏等[9]为使磁流变阻尼器的动力响应和阻尼范围最大化，采用NSGA-III算法对磁流变阻尼器进行了几何尺寸的优化。结果表明多目标优化设计后的磁流变阻尼器更好的满足了制造和应用的要求。邓召学等[10]为提高磁流变悬置的阻尼力和隔振性能，采用非支配排序遗传算法对磁路进行优化。结果表明，优化后的磁流变悬置的可控性和隔振性能都有明显改善。章新杰等[11]为了提高磁流变阻尼器的动态性能和散热性能，采用快速多目标遗传算法对结构参数进行优化，优化后的阻尼器能实现动态性能、散热效率和结构柔性的完美平衡。郑玲等[12]以线圈消耗功率以及活塞体积为目标函数，阻尼力可调和时间响应常数作为约束条件，线圈参数作为设计变量，采用有限元方法对磁流变减振器进行优化设计。结果表明，优化后的磁流变减振器体积、线圈功率和时间常数明显减小，优化后的阻尼器性能更好。

目前学者们只是采用不同的优化目标对磁流变阻尼器单体进行优化，不能体现出阻尼器在整车动力学模型的隔振效果。因此，需要将磁流变阻尼器嵌入整车动力学模型内，对磁流变阻尼器的结构参数优化。考虑悬架的刚度和阻尼以及轮胎的刚度，建立车身3自由度以及4个非簧载质量构成的七自由度整车动力学模型。通过多学科优化设计平台ISIGHT软件搭建了基于整车七自由度动力学模型优化平台，并对整车模型内磁流变阻尼器的磁路结构参数进行优化分析。

1 磁流变阻尼器结构设计

本文提出具有锥形倾斜角度阻尼通道的磁流变阻尼器，如图1所示，主要由吊环、活塞杆、拉伸腔、压缩腔、缸体、浮动活塞、阻尼通道以及励磁线圈等组成。当磁流变液充满阻尼器时，给励磁线圈通入电流，由于电磁效应，磁芯与锥形阻尼通道间产生磁场回路，磁场方向与磁流变液流动方向垂直。磁流变液在压力作用下通过阻尼通道时，在外加磁场的作用下迅速由牛顿流体变成半固体或者固体，产生的磁感应强度随着外加磁场的增大而增加。磁流变液想要通过阻尼通道，就需要克服阻尼力，因此阻尼通道两端压差就会增加，从而实现减缓或者阻止液体流动。通过施加电流或改变阻尼通道的倾斜角度，控制磁感应强度，进而控制磁流变阻尼器产生的阻尼力，从而实现对阻尼力的调节。

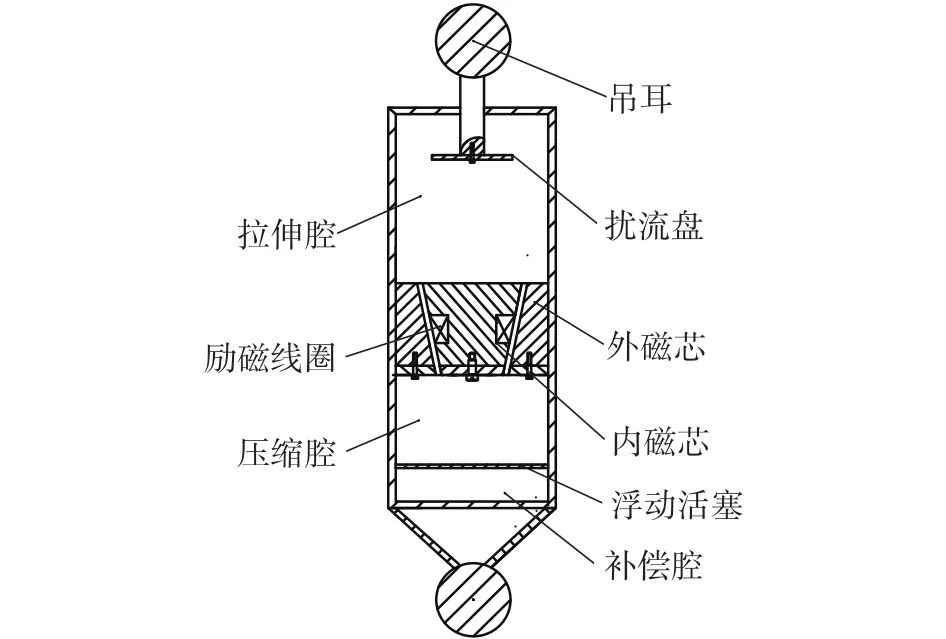
图1 磁流变阻尼器结构示意图

决定磁流变阻尼器性能最主要的部分是磁芯，磁芯设计的好坏直接影响阻尼器隔振性能。如图2所示，改变倾斜角度、激励电流的大小可以改变磁感应强度，进而达到改变阻尼力的目的。

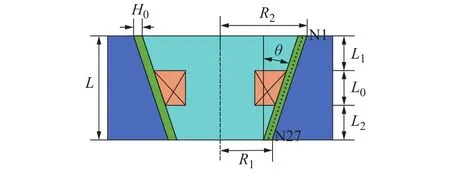
图2 磁流变阻尼器磁芯

2 数学模型及磁路分析

2.1 数学模型

当倾斜角度为0时即为径向流动通道，在平面上展开后是平行平板间隙流动的问题，黏性压降为[13]

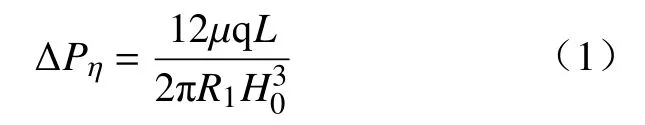
式中：R1为内磁芯内径；L为磁芯高度；H0为阻尼通道间隙宽度。

径向流动通道屈服压降公式[14]为

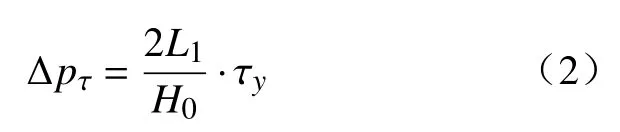
式中：L1为有效磁极长度，且L1=L2； τy为剪切屈服应力。

径向流动通道总压降为

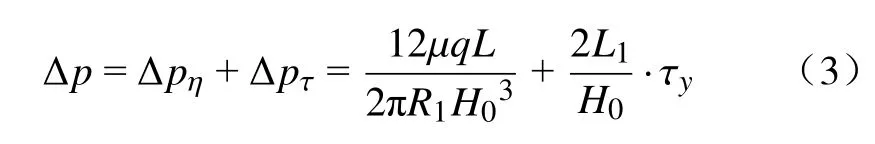
所提出的阻尼通道是具有锥形倾斜角度阻尼通道，假设锥形倾斜角度阻尼通道的延伸面相当于平行圆盘间隙的一部分，从平行圆盘模型中建立锥形模型。图3显示了锥形流动通道拓展表面图。

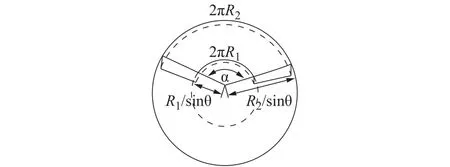
图3 锥形通道拓展表面图

拓展表面的中心角为

平行圆盘间隙的黏性压降为

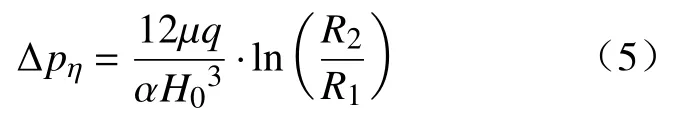
将式（4）代入式（5）得

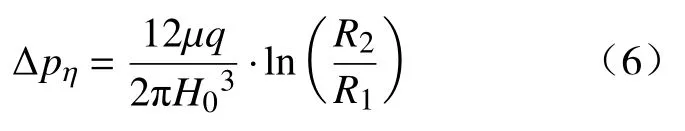
阻尼通道上侧有效磁极高度为L1，阻尼通道长度为

同理下侧有效磁极阻尼通道长度为

将式（7）和式（8）代入式（2）得锥形通道屈服压降为

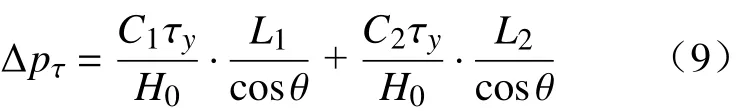
式中：C1，C2为修正系数，当时，C1，C2=3，当

可得，锥形通道总压降为

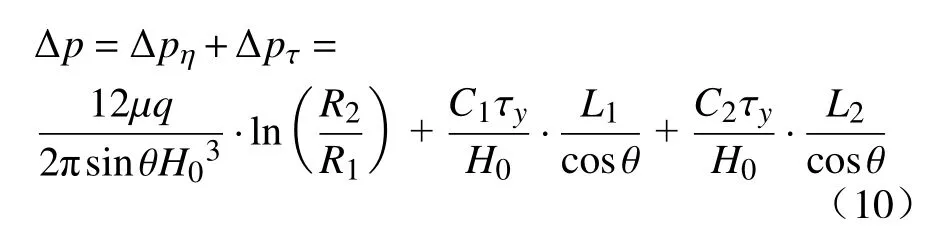
则，磁流变阻尼器输出阻尼力表达式为

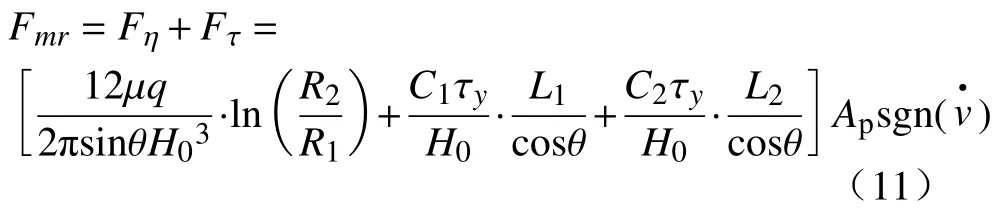
式中：Fη为黏性阻尼力；Fτ为库伦力；Ap为等效磁芯面积。

2.2 磁路分析

为观察磁路结构参数对磁感应强度的影响，建立有限元模型，并将其节点编号如图4表示出来。

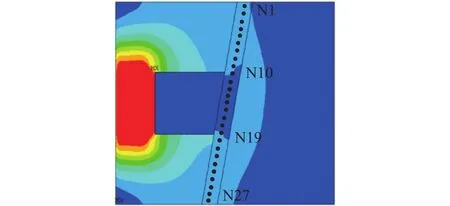
图4 有限元模型及节点编号

采用有限元的方法对阻尼间隙H0、倾斜角度 θ、内径尺寸R1进行分析，如图5所示。采用径向阻尼通道的磁流变阻尼器，阻尼间隙磁感应强度随着内径R1的增加，磁感应强度逐渐增加，当内径R1足够大时，阻尼间隙内磁感应强度趋于饱和；但是当给阻尼间隙一个5°的倾斜角度时，即本文所采用的锥形倾斜角度阻尼通道磁流变阻尼器。在内径R1保持不变时，增加倾斜角提高了阻尼间隙内平均磁感应强度的饱和点。

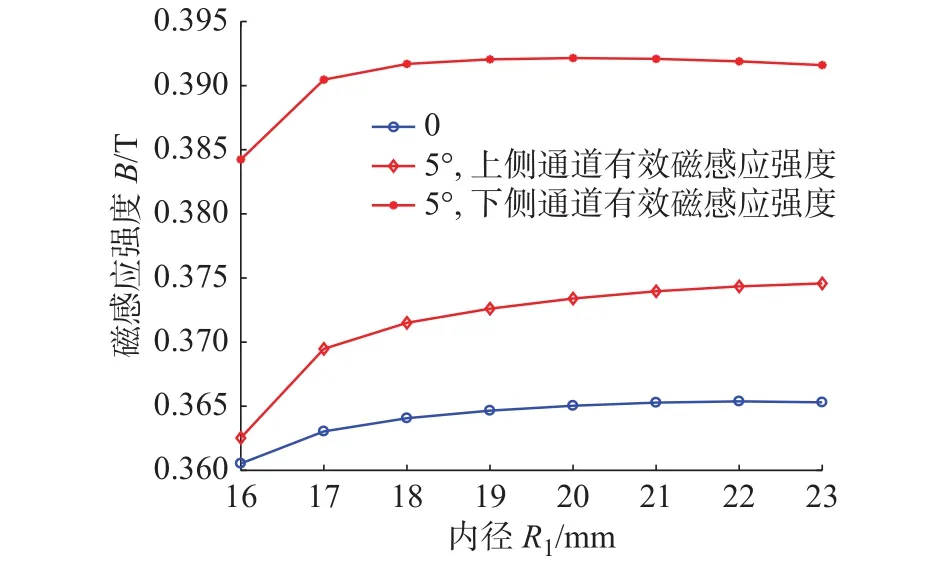
图5 径向通道与倾斜通道磁感应强度对比图

电流强度I=1A，根据《汽车减振器技术条件与台架试验方法》和《汽车筒式减振器尺寸系列及技术条件标准QC/T 491−1999》，减振器工作缸筒直径的取值范围为 20 ~ 65 mm。初始参数如表1 所示。

表1 初始结构参数

不同内径下阻尼通道间隙处磁感应强度曲线如图6所示。由图6可知，随着内径尺寸R1的增加，磁感应强度值也随之增加；当内径尺寸增加到18 mm后，上下两侧有效磁极区域磁感应强度趋近于饱和。

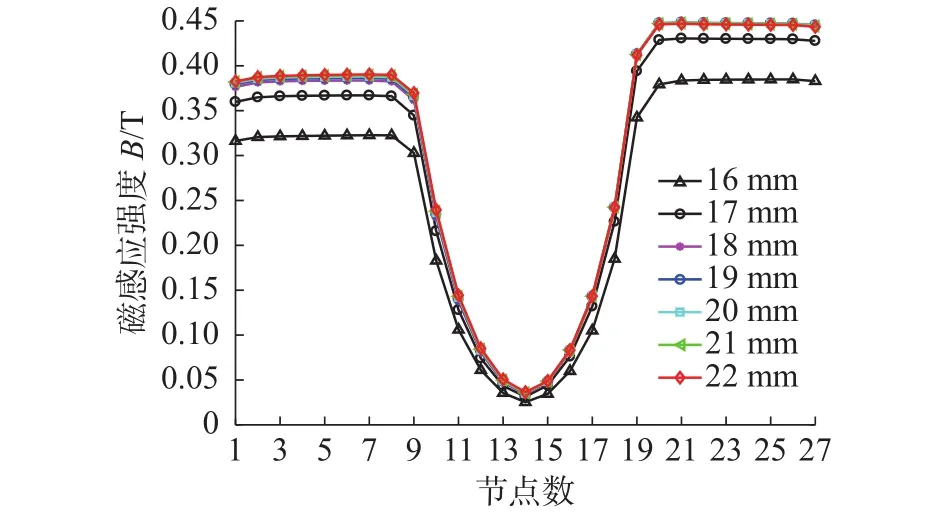
图6 不同内径下阻尼通道间隙处磁感应强度曲线

不同间隙下阻尼通道磁感应强度曲线如图7所示。由图7不难看出，随着阻尼间隙H0的增加，磁感应强度值也随之减少；且下侧有效磁极区域磁感应强度大于上侧磁感应强度。

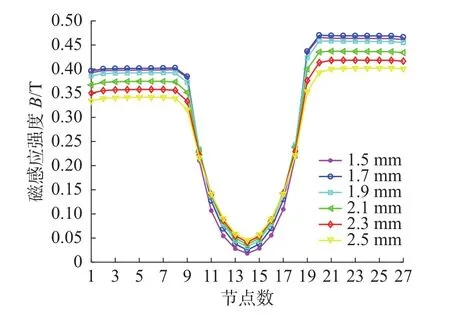
图7 不同间隙下阻尼通道磁感应强度曲线

随着倾斜角度的增加，阻尼通道有效磁极处磁感应强度呈现出先增加后减少的趋势，突变角度为15°，如图8 所示。在 0 ~ 20°时，随着角度的增加，上侧磁感应强度逐渐增大，当倾斜角度大于20°时，随着角度的增加，磁感应强度逐渐减小，此时上侧通道有效磁极区域的突变角度为 20°；在 0 ~ 15°时，随着角度的增加，下侧磁感应强度逐渐增加，当倾斜角度大于15°时，随着倾斜角度的增加，磁感应强度逐渐减小，此时下侧有效磁极的突变角度为15°。

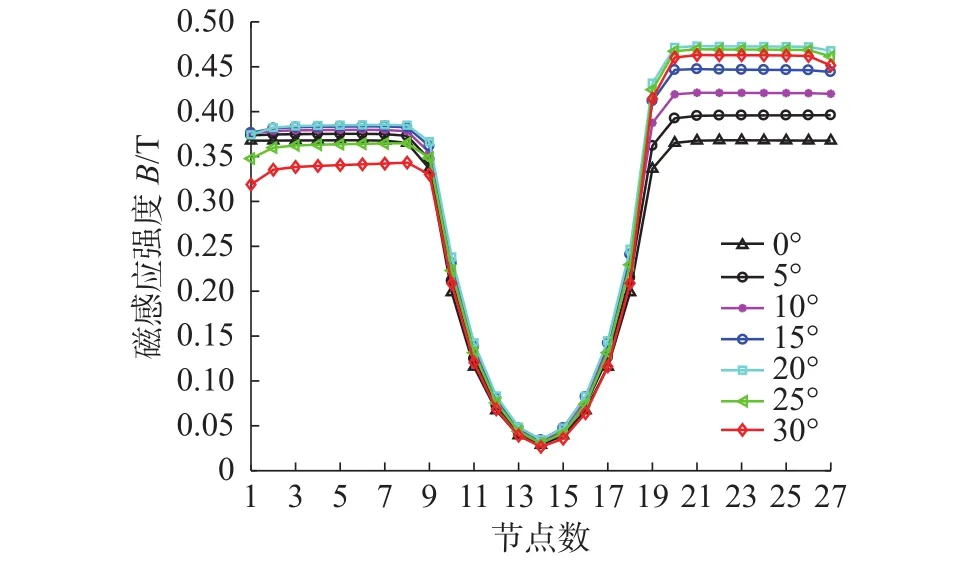
图8 不同倾斜角度下阻尼通道磁感应强度曲线

对上述结构参数的分析可知，磁路结构参数变化对阻尼器磁感应强度有较大的影响，而磁感应强度的改变会引起磁流变阻尼器输出阻尼力波动，进而影响整车动力学性能[14]。因此，针对磁路的结构参数进行优化是改善车辆动力学性能的有效手段。

3 协同优化平台搭建

3.1 路面激励分析

3.1.1 离散冲击路面激励

本文采用过减速带时轮胎受到的激励为车辆过离散路面的冲击激励，图9为路面减速带模型。为方便分析将激励模型用三角函数来表征。

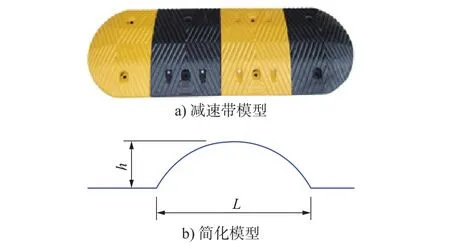
图9 减速带模型

减速带激励的数学模型为：

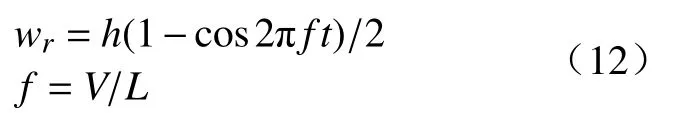
式中：L为减速带宽度；h为 减速带高度；V为行驶车速。

3.1.2 连续随机路面激励

路面断面曲线如图10所示。

图10 路面断面曲线

通常情况下，采用空间频率功率谱密度来表征随机路面，根据GB/T 7031可知路面功率谱密度[16]为

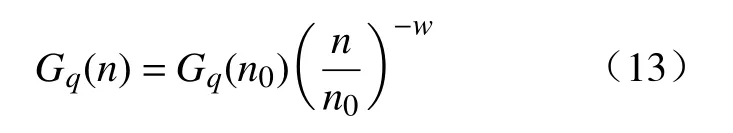
式中：n0为参考空间频率，n0=0.1m−1；Gq(n0)为路面不平度系数，m3。

当分级路面谱频率指数为2时，速度功率谱密度为

式中f为时间频率。

因此，在时间频率范围内，当V恒定时速度功率谱密度为常数，此时称为“白噪声”。

3.2 建立整车七自由度模型

阻尼器单体优化未考虑对整车性能的影响，因此需要在整车模型内对其进行分析。图11为包含车身垂向、侧倾、俯仰3个自由度和4个非簧载质量垂向运动的整车七自由度动力学模型。

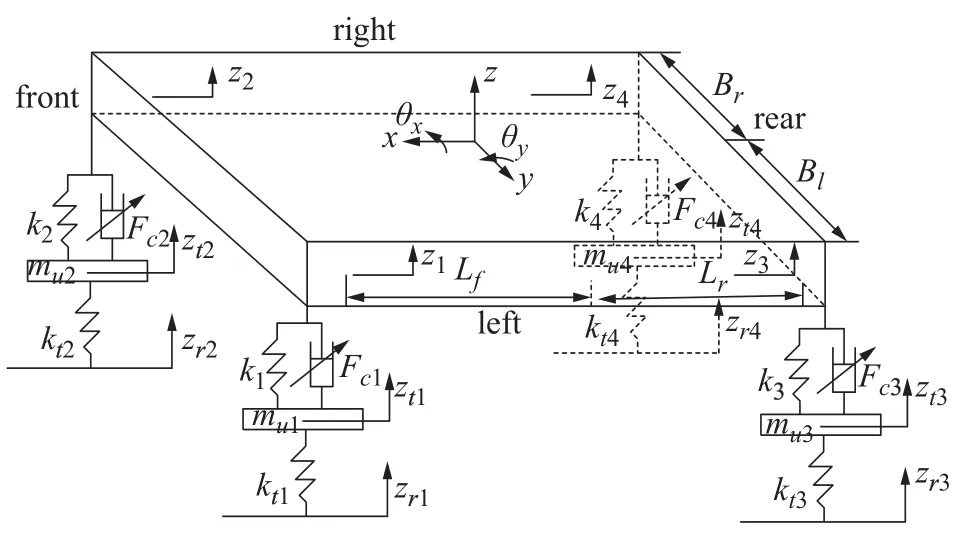
图11 七自由度整车模型

车身运动学方程为：

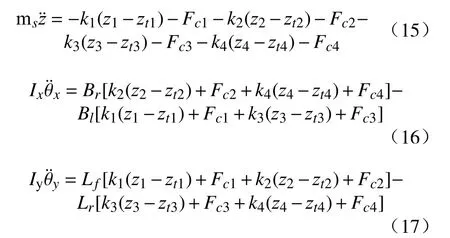
4个非簧载质量的垂向运动学方程为：

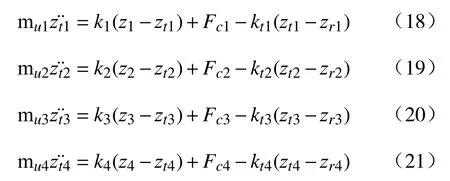
假设整车底盘为刚体，当俯仰角和侧倾角较小时，底盘4个端点处的垂向位移为：

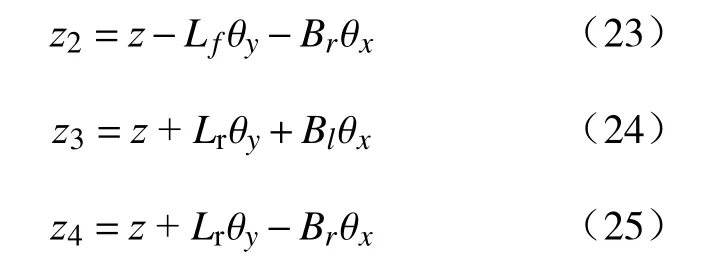
式中：ms为簧载质量；Ix为簧载质量绕纵轴的转动惯量；Iy为簧载质量绕横轴的转动惯量；mu1，mu2，mu3，mu4分别为前左、前右、后左、后右的非簧载质量；Fc1，Fc2，Fc3，Fc4分别为4个车轮的阻尼力；Bl为簧载质量质心与左轮的横向距离；Br为簧载质量质心与右轮的横向距离；Lf为簧载质量质心与前轴的距离；Lr为簧载质量质心与后轴的距离；k1、k2为前轴左右两侧弹簧刚度，k3、k4为后轴左右两侧弹簧刚度；kt1、kt2为前轴左右两侧轮胎刚度；kt3、kt4为后轴左右两侧轮胎刚度。

建模过程所采用的参数如表2所示。

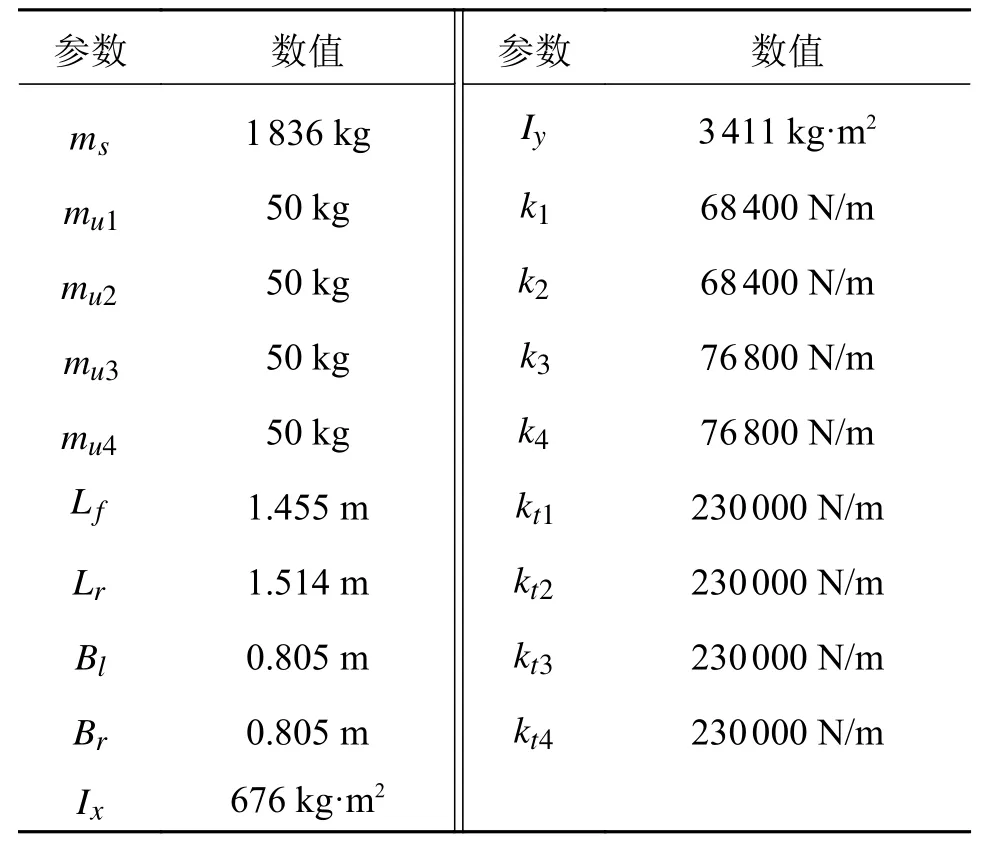
表2 七自由度整车模型参数

3.3 优化平台搭建

利用 ISIGHT、ANSYS和 MATLAB/Simulink软件搭建协同仿真优化平台，实现阻尼器磁路多目标优化。以匀速工况和过减速带工况悬架动挠度、车身垂向加速度、轮胎动载荷三者的均方根值最小为优化目标，磁路结构参数阻尼间隙H0、倾斜角度θ、内径尺寸R1、磁芯长度L1作为设计变量，阻尼通道有效磁极处磁感应强度B≥0.4T作为约束。在基于整车七自由度动力学模型的磁流变阻尼器结构优化过程中，首先，通过ISIGHT调用ANSYS APDL对阻尼器磁路进行参数化建模，并完成电磁场分析。其次，根据APDL有限元分析的磁感应强度和磁路的结构参数，通过ISIGHT调用MATLAB完成阻尼力计算，再调用MATLAB/Simulink模块分别计算七自由度不同工况下悬架动挠度、车身垂向加速度、轮胎动载荷的均方根值。求解过程采用非支配排序的遗传算法（Non-dominated sorting genetic algorithm Ⅱ, NSGA-Ⅱ）作为优化算法[17]，种群数和优化代数分别为20和50，优化的原理如图12所示。通过ISIGHT调用仿真软件进行迭代计算后输出最优设计变量[18]。

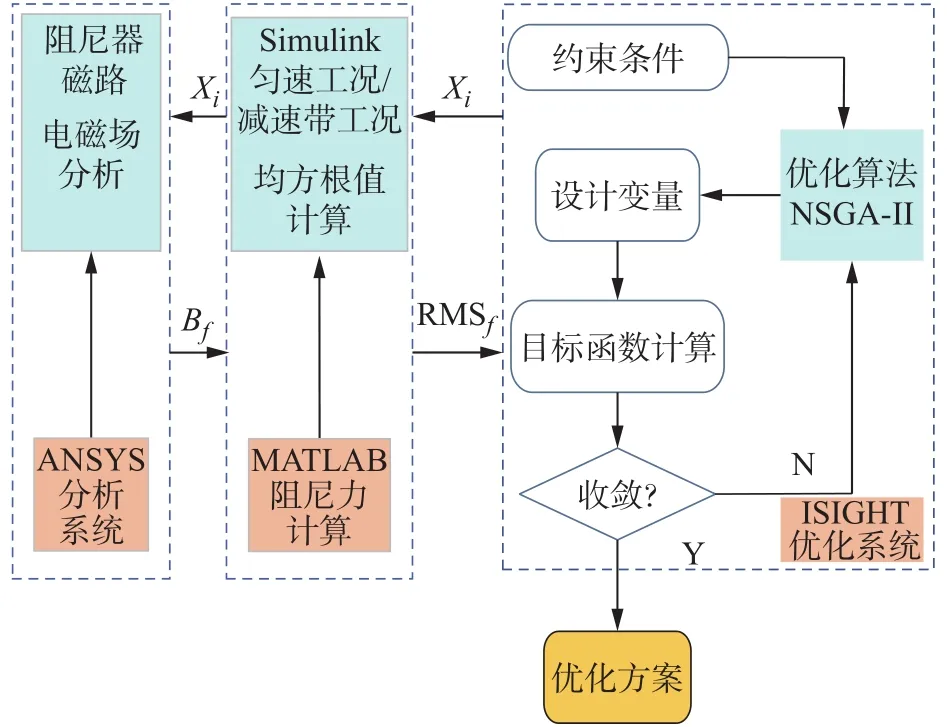
图12 优化原理图

4 优化结果及分析

迭代计算结束后，得到基于整车动力学模型优化前后的结构参数如表3所示。

表3 优化前后结构参数

图13是优化前后有效阻尼通道磁感应强度对比，由节点磁感应强度曲线可以看出，与优化前相比，优化后节点处磁感应强度得到了较大的提高。上侧阻尼通道磁流变液的平均磁感应强度由0.38 T提高至0.42 T，下侧阻尼通道磁流变液的平均磁感应强度由 0.44 T 提高至 0.51 T。

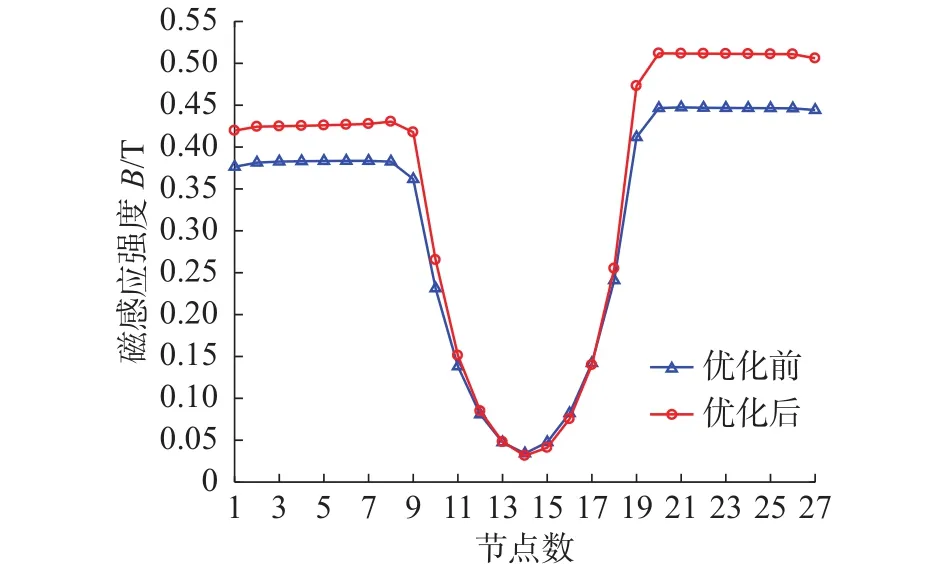
图13 优化前后磁感应强度对比

图14、图15是车辆在匀速工况和过减速带工况优化前后阻尼力对比图，优化后带倾斜角度阻尼器的阻尼力比优化前无倾斜通道和带倾斜通道阻尼器的阻尼力都更大，车辆平顺性和操稳性有明显改善。

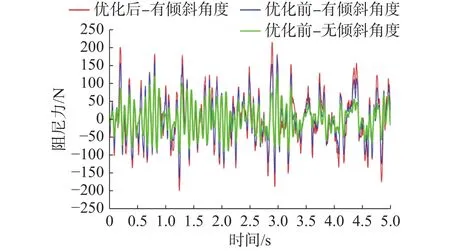
图14 匀速工况优化前后阻尼力对比

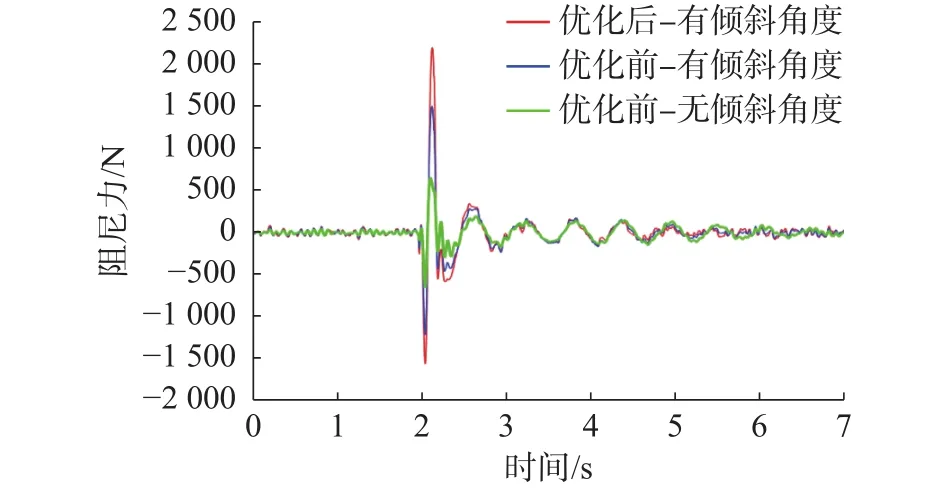
图15 过减速带工况优化前后阻尼力对比

表4、表5为优化前后匀速行驶工况和过减速带工况优化前后悬架动挠度、轮胎动载荷、车身垂向加速度三者均方根值。

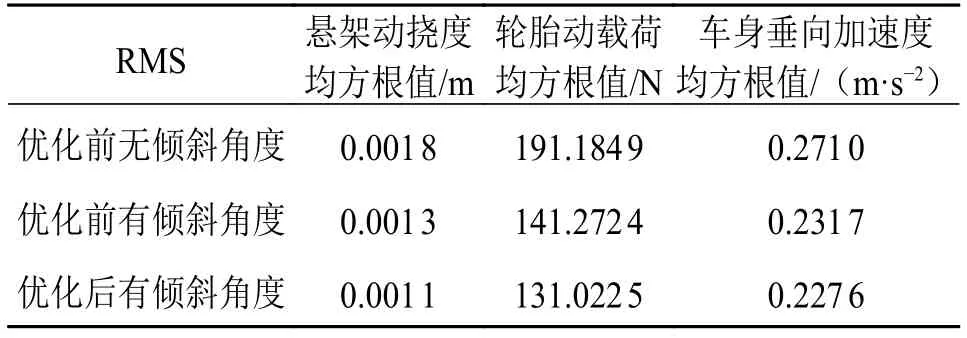
表4 优化前后匀速工况均方根值

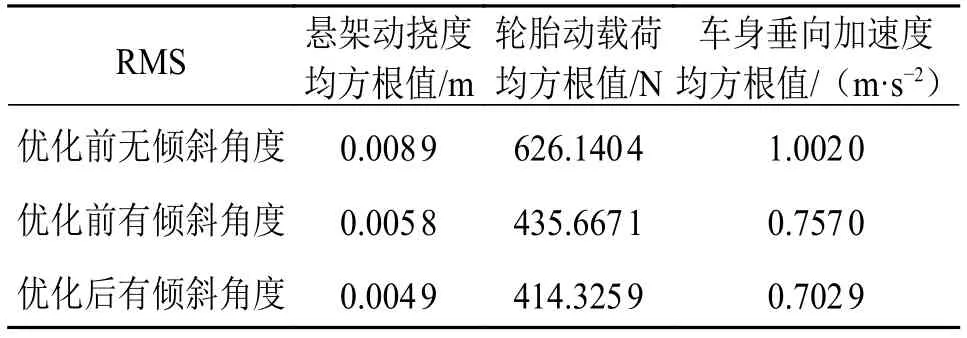
表5 优化前后过减速带工况均方根值

图16显示了车辆在B级路面60 km/h匀速行驶优化前后图形对比，结合表4可以看出，基于整车动力学模型的锥形倾斜角度磁流变阻尼器结构优化后相比于未优化锥形倾斜角度磁流变阻尼器的悬架动挠度、轮胎动载荷、车身垂向加速度均方根值分别减少了15.38%，7.26%，1.77%；优化后锥形倾斜角度的磁流变阻尼器相比于优化前无倾斜角度的磁流变阻尼器的悬架动挠度、轮胎动载荷、车身垂向加速度均方根值分别减少了38.89%，31.47%，16.01%；锥形倾斜角度的磁流变阻尼器匀速工况优化后，车辆的悬架动挠度和轮胎动载荷得到了明显的改善，车身垂向加速度有较小的改善。

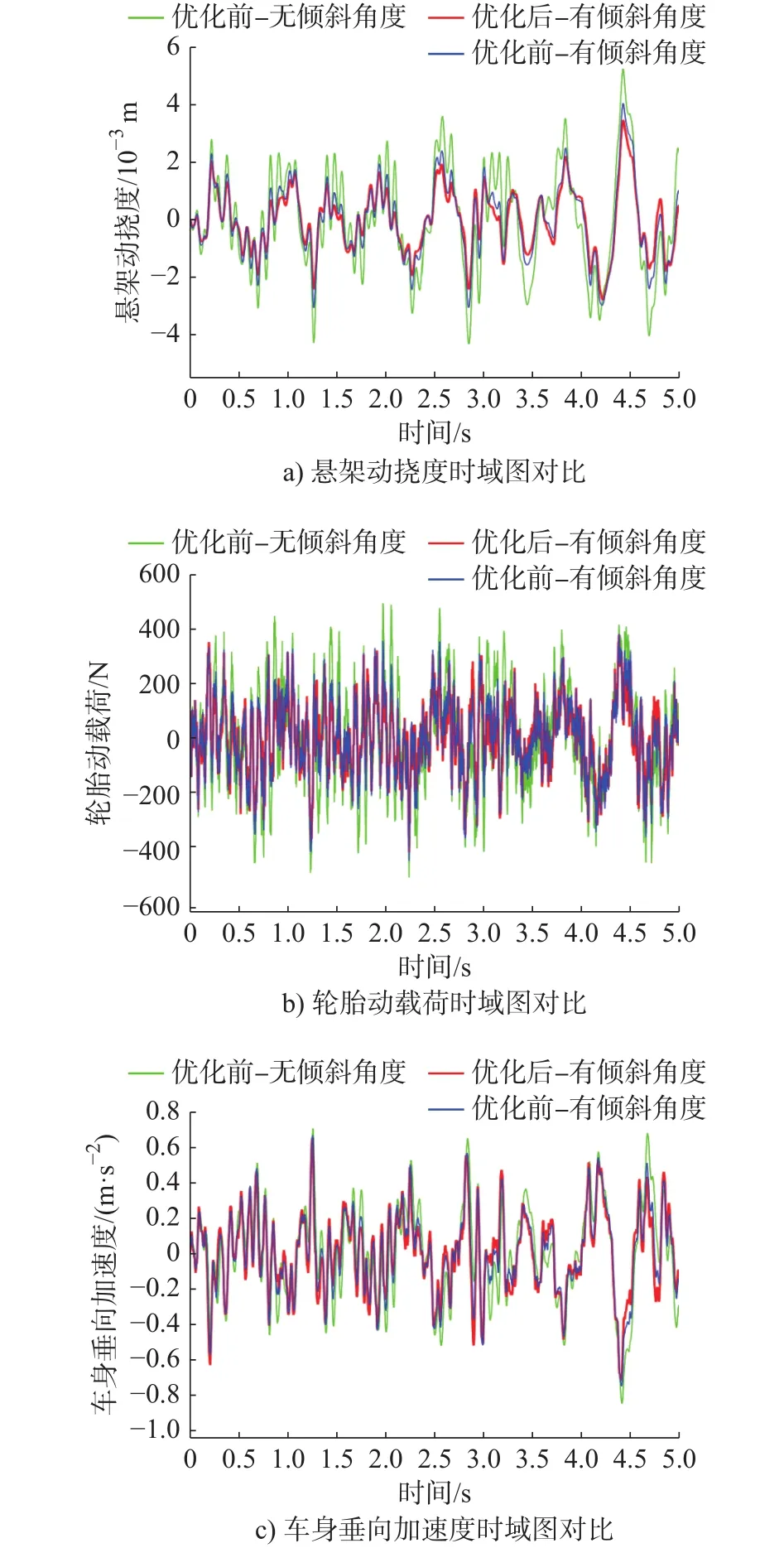
图16 匀速工况下优化前后的时域图

图17为车辆在10 km/h过减速带工况下优化前后图形对比，结合表5可知，基于整车动力学模型锥形倾斜角度的磁流变阻尼器优化后相比于优化前锥形倾斜角度的磁流变阻尼器的悬架动挠度、轮胎动载荷、车身垂向加速度均方根值分别减少了15.52%，4.90%，7.15%；优化后锥形倾斜角度的磁流变阻尼器相比于优化前无倾斜角度的磁流变阻尼器的悬架动挠度、轮胎动载荷、车身垂向加速度均方根值分别减少了44.94%，33.83%，29.85%；锥形倾斜角度的磁流变阻尼器过减速带工况优化后，车辆的悬架动挠度和车身垂向加速度得到显著的提高，轮胎动载荷也有所改善。

图17 过减速带工况下优化前后时域图

综合上述分析结果可知，B级路面60 km/h匀速行驶工况和车辆10 km/h通过减速带工况的整车动力学模型中，基于整车动力学模型优化的锥形倾斜角度磁流变阻尼器隔振性能与初始设计的磁流变阻尼器相比较，悬架动挠度有明显的提高，轮胎动载荷和车身垂向加速度有一定的提高；具有锥形倾斜角度的阻尼器相比无倾斜角度的阻尼器能够更好改善车辆的性能，总体来说，车辆的平顺性和操稳性都得到了相应的改善，NVH性能得到明显提升。

5 结论

本文提出了一种具有锥形倾斜角度阻尼通道的磁流变阻尼器，并基于多学科优化软件ISIGHT搭建了基于整车动力学模型的磁流变阻尼器结构优化平台，对锥形倾斜角度阻尼器的磁路结构参数进行了优化。优化结果表明，优化后的锥形倾斜角度阻尼器具有更高的磁感应强度饱和点，阻尼力可调范围更大；在匀速工况和过减速带工况下，悬架动挠度、车身垂向加速度和轮胎动载荷的均方根值小于初始设计的值，悬架动挠度具有明显的改善，车身垂向加速度和轮胎动载荷有些许的改善。总的来说，基于整车动力学模型优化后的磁流变阻尼器能够更好提高车辆的平顺性和操稳性。