高速磁浮列车动力学性能参数多目标优化方法研究

安东，邹益胜，赵春发，梁红琴* , ，冯洋，刘奇锋

（1.西南交通大学 机械工程学院，成都 610031；2.西南交通大学 牵引动力国家重点实验室，成都 610031）

随着磁浮列车的不断发展，设计速度不断提升，本文研究的600 km/h高速磁浮列车系统较上海德国TR08磁浮列车最高运行速度430 km/h有显著提高。为满足时速600 km/h的车辆动力学性能要求，需要对磁浮车辆关键部件进行优化设计。通过研究适用于高速磁浮列车的多目标优化方法，提出磁浮车辆悬挂参数、轨道梁刚度参数、悬浮控制参数等优化建议。基于仿真计算模型的数值模拟分析方法被广泛应用于磁浮列车性能参数的分析和优化[1-8]。基于仿真计算模型的优化方法在优化过程中会反复调用仿真计算模型进行大量计算，由于仿真计算模型计算耗时的特点，常出现优化周期过长等问题，使优化过程难以进行。

代理模型可基于少量的仿真数据构建，构建完成后能够近似代替仿真计算模型，可简化计算，缩短计算周期。Hosder等[9]为了解决高速民用飞机的MDO问题，基于多项式响应面代理模型方法构建了飞机航程与空气动力学参数之间的近似模型。龙腾等[10]提出基于自适应径向基函数代理模型的多目标优化策略，解决了翼型气动隐身优化设计存在的计算耗时问题，提高了翼型升阻比，并且显著缩短了优化设计周期。聂雪媛等[11]在大型飞机设计过程中由于直接调用CFD/CSD耦合分析方法出现计算量过大和优化时间过长的问题，采用Kring方法建立代理模型对飞机结构刚度进行了优化设计。张剑[12]构建BP神经网络代理模型用于高速列车悬挂参数和车辆结构的优化设计，提高了车辆的动力学性能。周家林等[13]为降低高速列车气动阻力，构造6个设计变量关于空气阻力的响应面函数对列车头型优化设计，使空气阻力值降低10.8%。Wang 和Shan[14]讨论了代理模型在其它工程领域的应用，均体现出显著的计算优势。对于代理模型在磁浮列车中的应用，现少有文献提及。

针对具有高非线性特点的高速磁浮列车动力学性能参数优化问题，讨论了不同代理模型构建方法的应用场景和预测精度，采用合适的代理模型方法构建出高速磁浮系统优化设计变量与性能指标之间的近似模型。为了获得准确的代理模型构建样本，基于HST-DCSP建立出高速磁浮列车分布式协同仿真模型。采用NSGA-Ⅱ优化算法在给定设计空间进行全面搜索，获得最优设计参数，为缩短高速磁浮列车研发周期，快速推进技术创新提供了理论参考。

1 高速磁浮列车系统分布式协同仿真模型

以德国TR08高速磁浮列车系统为参考对象，考虑悬浮导向控制、部件弹性以及轨道梁弹性等因素的耦合作用，构建出机-电耦合、结构刚-弹性耦合的仿真模型[15]。采用SIMPACK建立磁浮车辆动力学模型，ANSYS建立轨道梁有限元模型。仿真模型计算过程需要实现车-桥仿真数据的交互，以某一软件为主导的单一环境下的耦合仿真，难以实现仿真数据的准确交互，使得仿真结果脱离实际。为获得精确的高速磁浮列车代理模型构建样本，需要建立出能够有效模拟高速磁浮列车实际运行状况的仿真模型。HST-DCSP是一种高速列车分布式耦合仿真平台，能够实现仿真数据的准确交互，因此，基于HST-DCSP建立出高速磁浮列车分布式协同仿真模型。高速磁浮系统基本参数如表1所示。

表1 高速磁浮系统基本参数

磁浮列车系统中自由度数和刚体数目较多，共包含有车体、4个悬浮架单元、14个悬浮电磁铁模块（28套悬浮控制器）、12个导向电磁铁模块（24套导向控制器）、2个制动电磁铁模块和16个空气弹簧。采用弹簧阻尼模拟力的作用，并通过调用SIMPACK软件中的Matsim接口来模拟电磁悬浮力和电磁导向力。单节高速磁浮列车动力学模型见图1。

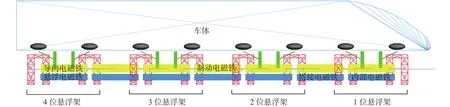
图1 单节磁浮列车动力学模型

磁浮轨道梁横截面见图2，其中定子和混凝土梁固结在一起，作为整体建立有限元模型[16]。由于磁浮车辆速度可达到600 km/h，为提供充足的运行距离以充分反映系统整体的动力学性能，设置线路总长1000 m。基于ANSYS软件采用Beam188梁单元建立25跨通用跨度轨道梁有限元模型如图3所示。

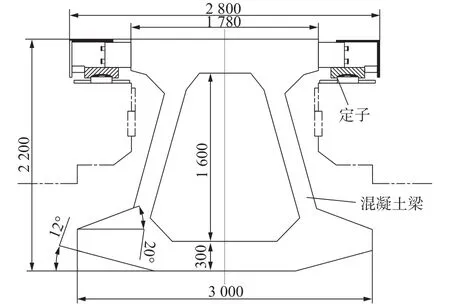
图2 磁浮轨道梁截面参数

图3 磁浮轨道梁有限元模型

为实现高速磁浮列车与轨道梁之间的高质量耦合，基于HST-DCSP高速列车分布式耦合仿真平台搭建出数据传输通道。HST-DCSP通过其耦合器子系统实现各仿真模块间的耦合，具有协调控制数据传输、仿真进程启停以及设置仿真步长等功能。磁浮列车动力学模型和轨道梁有限元模型基于HSTD CSP的耦合关系如图4所示。

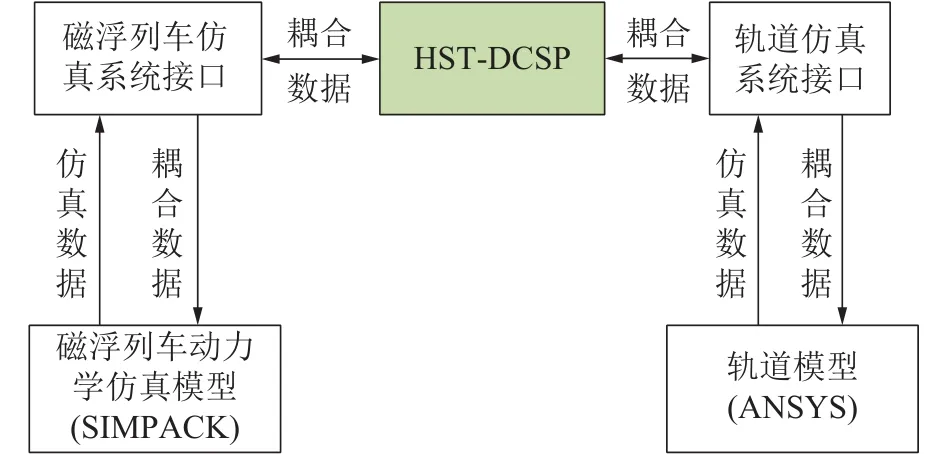
图4 各模块耦合关系图

2 高速磁浮列车系统代理模型

2.1 评价指标及待优化设计变量的确定

对于高速磁浮列车系统的动力学性能评估，基于专家领域中的先验知识，以头车第一位电磁铁模块前端的悬浮间隙、电磁铁线圈电流作为安全性评估指标；以头车中部和端部车厢底板的Sperling平稳性、车体垂向振动加速度作为平稳性评估指标；以悬浮架振动加速度评估磁轨动力作用水平；以轨道梁振动位移幅值和轨道梁振动加速度评估轨道状态。得出评价指标如表2所示。基于专家领域中的先验知识、考虑整个高速磁浮系统、考虑运行安全性和平稳性等多个方面综合确定出高速磁浮列车系统的关键设计变量。得出设计变量及其取值范围如表3所示。

表2 磁浮列车系统性能评价指标

表3 磁浮列车系统关键设计变量

为保证抽取样本均匀以充分获取特征信息，采用最优拉丁超立方试验设计方法[17-18]在设计变量X1~X5的取值区间进行抽样。为降低后续磁浮系统分布式协同仿真模型的计算时间，共抽取20组样本[19]。其中设计变量X1相对于其它4个设计变量的样本分布情况如图5所示，可见样本分布均匀，充满整个设计空间。以速度 600 km/h，直线线路 1000 m，作为计算工况，将20组样本代入磁浮系统分布式协同仿真模型进行计算，得出7项高速磁浮列车动力学性能评价指标值，至此得到可用于构建代理模型的完整样本。

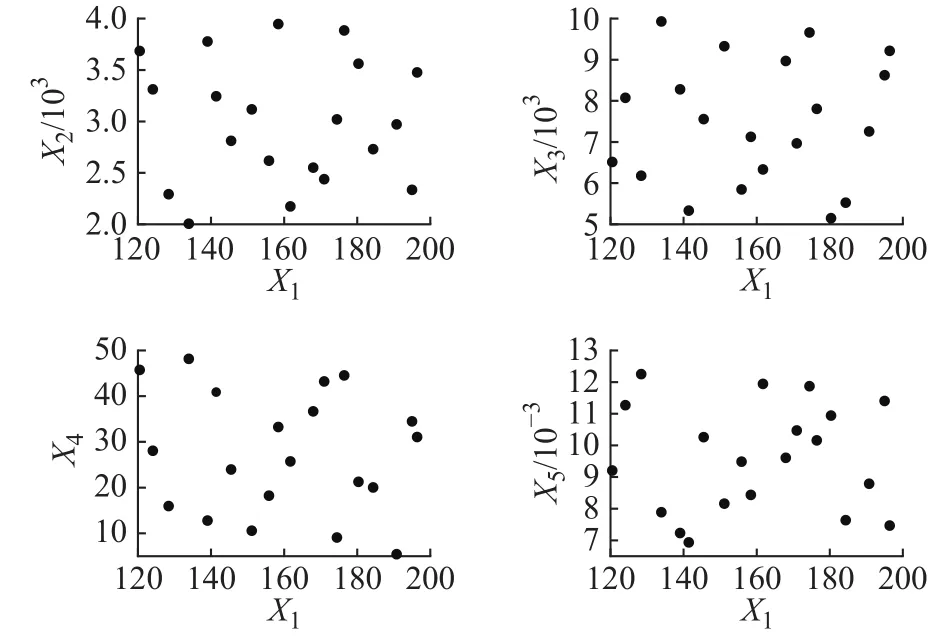
图5 设计变量 X1 相对设计变量 X2 ~ X5 样本分布情况

2.2 代理模型构建及精度分析

代理模型构建过程包括样本提取、模型构建及模型测试这3部分，其中模型构建是代理模型技术的主体。不同近似方法构建的代理模型用于解决不同的问题，分析不同研究对象，选取合适的近似方法是有效运用代理模型技术的关键。高速磁浮列车的性能参数优化设计涉及5个设计变量，7项性能指标，基于20组样本构建其代理模型属于高非线性、小样本问题。

张剑[12]在采用代理模型技术解决高速列车性能参数优化问题中讨论了不同代理模型方法的适用对象，指出BP神经网络能解决高非线性问题，仅需一个隐含层就能实现任意维度的准确映射。Hou 等[20]等分析了最小二乘支持向量机方法（Least squares support vector machine，LSSVM），得出具有解决小样本、非线性和高维度问题的特点。基于上述研究结果，以下将结合高速磁浮列车性能参数优化设计问题，讨论BP神经网络和LSSVM代理模型构建方法的适用性。

BP神经网络是一种前馈型网络，通过误差的反向传播来优化调整网络的权值和阈值以实现对数据的拟合。高速磁浮系统BP神经网络代理模型构建过程：设置隐含层数和初始节点数以确定出网络结构；导入2.1节中20组样本并进行归一化处理；设置传递函数、训练函数及训练参数；训练网络并测试网络预测精度。训练参数设置如表4所示。训练得出具有单隐含层、13个隐层节点数的5-13-7的BP神经网络代理模型。

表4 BP 神经网络训练参数设置

LSSVM是通过转换数据空间维度解决非线性问题，首先在原始空间对数据进行计算，再通过核函数将原始空间映射到高维空间，最后在高维空间实现对数据的拟合，其构建过程主要是对惩罚参数与核参数的调整过程[21]。本文中首先利用模拟退火算法搜索出LSSVM惩罚参数和核参数的初始值，然后利用单纯形法确定出最优值。设置LSSVM训练参数如表5所示。

表5 LSSVM 训练参数设置

基于表5中的训练参数，得出高速磁浮列车系统LSSVM代理模型，其惩罚参数与核参数值如表6所示。其中磁浮列车系统7项性能指标分别对应7个LSSVM代理模型。

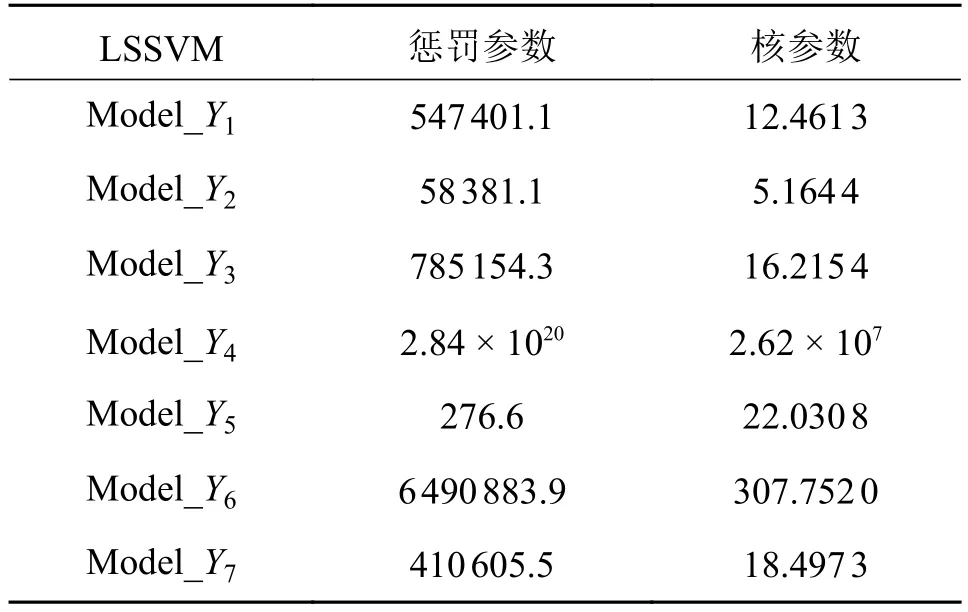
表6 LSSVM 惩罚参数与核参数值

为验证两种方法所构建的代理模型预测精度，基于最优拉丁超立方试验设计方法生成9组测试样本，采用平均相对误差对代理模型预测精度进行检验，7项性能评价指标Y1~Y7对比结果如图6所示。

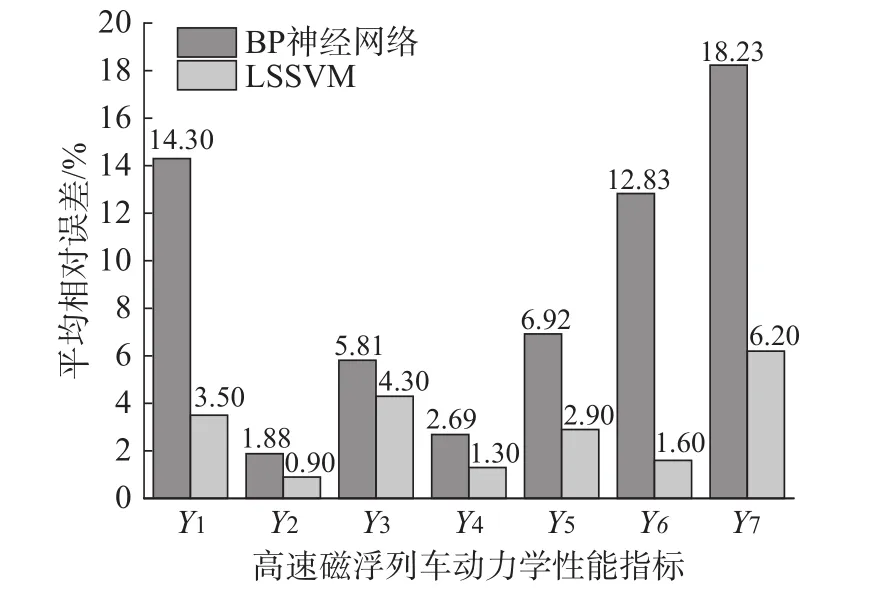
图6 BP 神经网络与 LSSVM 预测精度比较

由图6分析可知，LSSVM对7项性能指标的预测精度显著高于BP神经网络，最大误差仅6.2%，最低误差达到0.9%，具有很好的预测精度，因此采用LSSVM构建高速磁浮列车系统代理模型。将9组测试样本的LSSVM代理模型预测结果与磁浮系统分布式协同仿真模型的计算结果进行比较，Y1~Y7对比结果如图7所示，均具有较高的重合度。

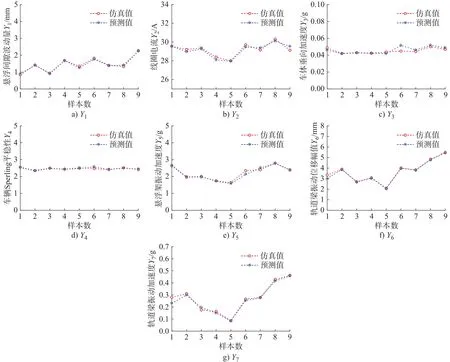
图7 性能指标 Y1 ~ Y7 仿真结果与代理模型预测值比较

3 高速磁浮列车参数优化设计

3.1 多目标优化模型

优化过程中，为减少各设计变量之间数量级的影响，统一进行归一化处理，使各设计变量在多目标优化模型中的取值区间均为[0,1]。基于LSSVM代理模型，以求解出各目标函数的最小值为优化方向，构建出多目标优化模型为

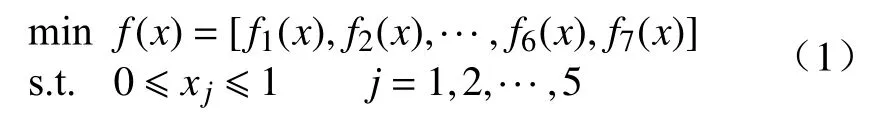
式中：x为5维变量，对应表3中5个关键设计参数；f(x)为7维目标函数矢量，对应表2中7项性能评价指标，与x的映射关系由LSSVM代理模型确定。

3.2 基于智能算法的优化计算

快速非支配排序和精英策略的遗传算法NSGA-Ⅱ是经典多目标优化算法，具有运行速度快，收敛性好的特点[22]。采用NSGA-Ⅱ算法在设计变量的取值区间进行优化解搜索，设置最优个体系数0.2，种群规模200，进化代数50。其中悬浮间隙波动量Y1的优化过程如图8所示。

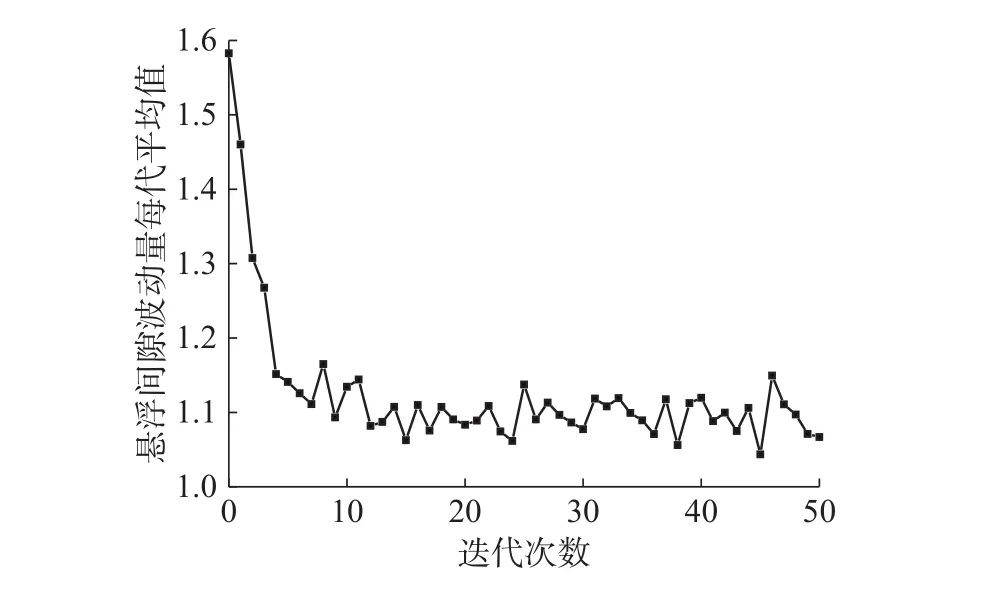
图8 悬浮间隙波动量寻优过程

优化共得出40组帕累托优化解，为验证优化结果的有效性，从帕累托优化解集中选取两组优化解，如表7所示，代入高速磁浮系统分布式协同仿真模型进行计算。将计算结果与高速磁浮系统初始性能进行比较，得到优化前后动力学性能情况如表8所示。

表7 设计变量优化结果

由表8分析可知，两组优化解的各项性能指标相比高速磁浮列车系统初始性能均得到提高。两组优化解的平均性能改善百分比均在30%左右，对于安全性指标Y1，优化解1改善41.16%，优化解2改善50.41%，改善效果后者高于前者；对于车体平稳性指标Y3、Y4，磁轨动力作用水平指标Y5以及轨道梁状态指标Y6、Y7，优化解1的优化效果高于优化解2。因此，可基于用户偏好选取优化解，若更注重车辆的安全性，则选取优化解1，如果以行车平稳性、磁轨及线路状态为偏好，则选择优化解2。

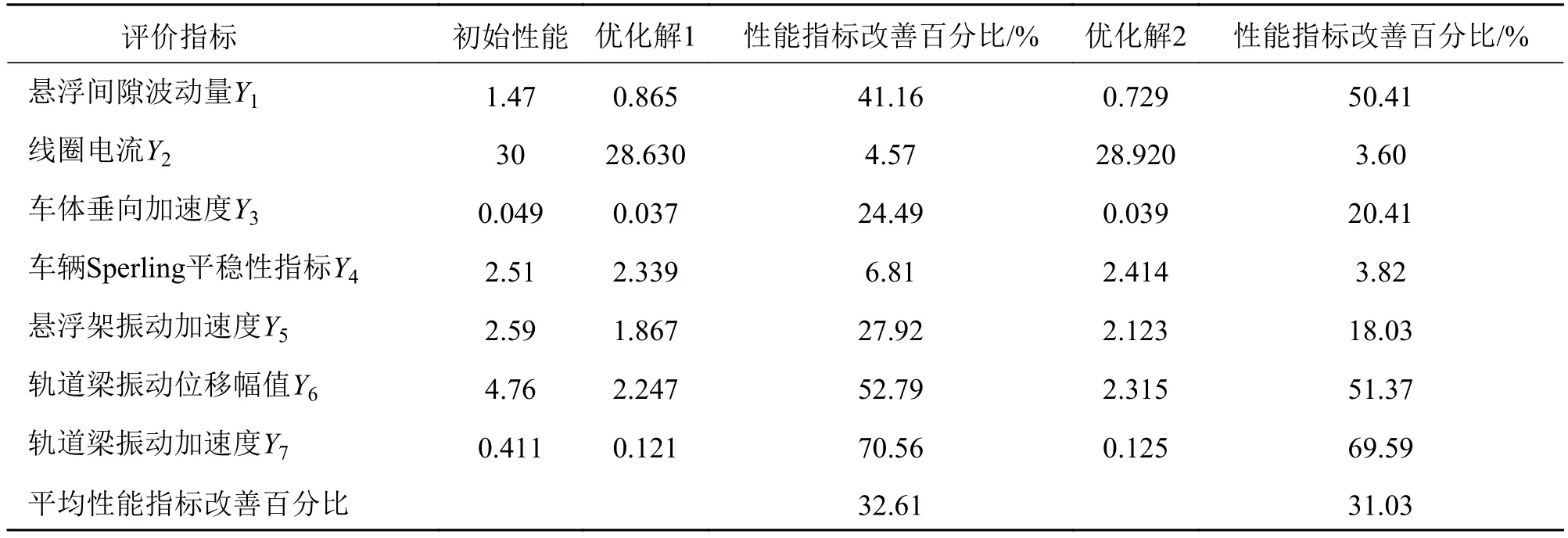
表8 磁浮列车系统优化前后动力学性能对比

4 结论

1）本文提出基于代理模型的高效多目标优化设计方法，考虑高速磁浮列车动力学性能参数优化问题的高非线性及小样本等特点，比较了BP神经网络与LSSVM在高速磁浮列车系统中的适用性。分析表明LSSVM的预测精度高于BP神经网络，且最大相对误差仅6.2%，可有效代替高速磁浮系统分布式协同仿真模型进行计算，解决了优化设计中仿真计算模型计算耗时的问题。

2）基于LSSVM代理模型，构建多目标优化模型，采用NSGA-Ⅱ算法进行优化求解。从Pareto解集中选取两组优化解仿真验证，结果表明高速磁浮系统7项性能指标均得到显著改善，并有效缩短了高速磁浮列车优化周期。