1/4悬架系统模型修正及悬架减振性能分析
2022-04-19黄腾逸周瑾孟凡许郭鑫星
黄腾逸,周瑾,孟凡许,郭鑫星
(南京航空航天大学 机电学院, 南京 210016)
磁流变悬架系统是基于磁流变阻尼器出力连续可调的一种半主动悬架系统,根据控制算法调节磁流变阻尼器出力来减小悬架的振动。一般控制算法的控制效果依赖于悬架的模型准确性,因此需要通过建立一个准确的磁流变悬架系统动力学仿真模型。
Bidikli[1]建立了1/4主动悬架系统的传递函数模型,并通过参数辨识得到该模型的参数。Zhang等[2]分析了车辆悬架的结构并以纯轮胎理论模型为输入建立了悬架多体系统动力学模型。周长峰等[3]提出了一种座椅悬架参数辨识方法。周长城等[4]也提出了一种座椅悬架等效刚度与等效阻尼的辨识方法。胡国良等[5-6]根据百分比斜率均方根值对磁流变阻尼器的结构参数对半主动悬架的减振性能影响进行分析,得到不同结构对车身加速度与悬架动行程的影响规律。孟广耀等[7]分析了磁流变半主动悬架各参数对运行平顺性的影响规律,确定了最优的半主动悬架设计参数。
通过模型修正的方法能建立准确的磁流变悬架系统动力学仿真模型,该模型能准确的模拟悬架系统在时域与频域上的振动响应,在此基础上可以分析阻尼器结构参数对悬架系统减振性能的影响。
1 阻尼器出力及悬架系统建模
1.1 阻尼器出力分析
磁流变液在动态剪切场作用下,其性能在不断变化,即在黏弹性与黏塑性之间不断跳动。为此参考阻尼器参数化动力学模型的演化与改进[8],对磁流变液的Bingham本构也进行相应的改进。
在Bingham本构模型的基础上再串联一个理想弹性单元,其应力应变关系如图1所示。
因此其本构方程为:
式中:γs为黏性应变;γp为弹性应变;ηp为弹性黏度;ηs为牛顿黏度;τ(H)为磁致剪切屈服强度。
根据串联本构的本构方程可发现,此时磁流变阻尼器中的弹性出力等于其黏性出力,另外由于活塞杆与密封圈之间存在摩擦力,此时阻尼器出力与修正阻尼器的Bingham参数化动力学模型类似[9],即
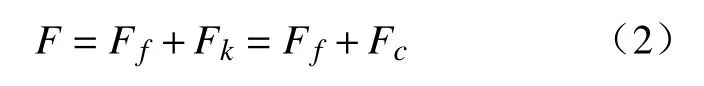
式中:Fk为弹性力;Fc为阻尼力;Ff为摩擦力。
阻尼器的阻尼出力为流体流动出力与压差出力之和,即
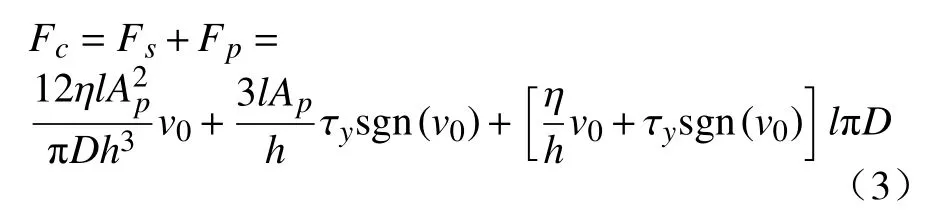
式中:η为流体黏度;l为活塞有效长度;Ap为活塞有效面积;v0是活塞的剪切速度;D为活塞直径;h为阻尼间隙宽度;τy为流体屈服强度。
此时磁流变阻尼器的剪切刚度k可以参考磁流变弹性体减振器的剪切刚度计算公式[10],即

式中:G'为储存模量;Ah为活塞的剪切面积。
根据Ginder[11]的研究可知储存模量G'与磁流变液的体积分数以及施加的磁场强度有关,即

式中:φ为磁流变液的体积分数;μ0为真空磁导率;Ms为磁流变液的饱和磁化强度;H为磁流变液的磁场强度。
1.2 道路谱仿真
现实中的道路不是一个光滑平面,而是一个粗糙表面,而通常人们将其与基准平面沿道路走向的高度差分布称为路面不平度函数,如图2所示。
图2 路面不平度
国际标准ISO 8608:2016[12]和国家标准GB/T 7031−1986[13]将路面位移不平度功率谱密度定义为
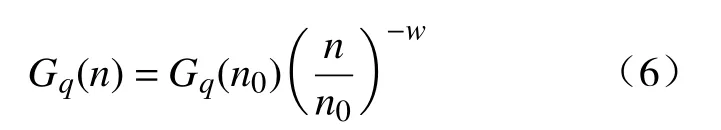
式中:n为空间频率,1/m;n0为参考空间频率,n0=0.1,1/m;w为路面谱的频率指数,一般情况下,w=2;Gq(n0)为路面不平度系数,m2/m−1。在参考空间频率n0下的道路谱功率密度值,其取值如表1所示[14]。
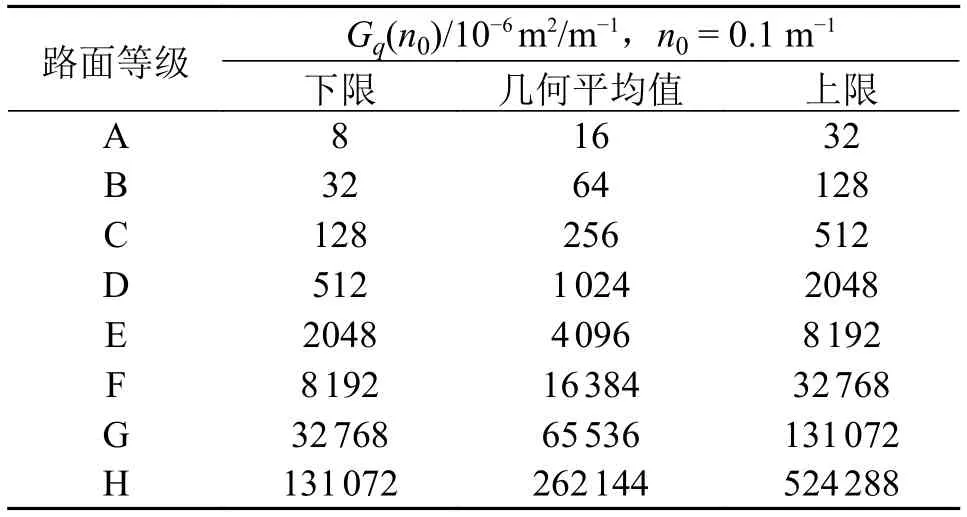
表1 各路面等级的路面不平度系数
根据滤波白噪声法可得在空间域上的路面激励的微分方程为
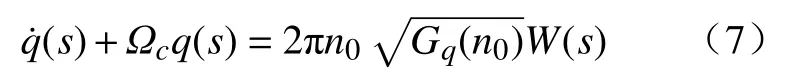
式中:Ωc为路面空间截止角频率,Ωc= 2πnc,nc为路面空间截止频率,nc= 0.01,1/m;W(s)为空间域内的平稳白噪声信号。
根据空间与时间的转换关系,得到

把式(8)代入式(7)得到在时间域上的路面激励微分方程为
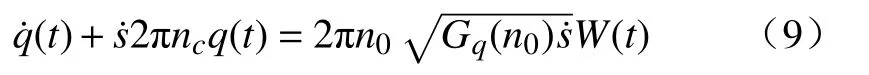
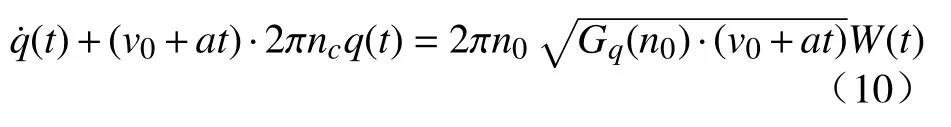
式中:v0为车辆行驶初始速度;a为车辆行驶加速度。
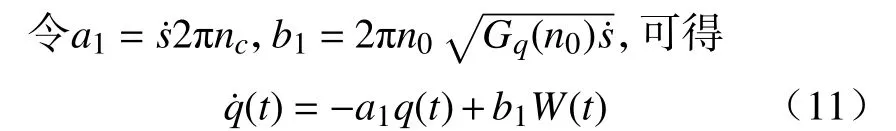
图3为根据式(11)在Simulink中仿真得到的60 km/h车速下的C级道路谱。根据图4可以发现仿真得到的道路谱信号满足道路谱信号标准。
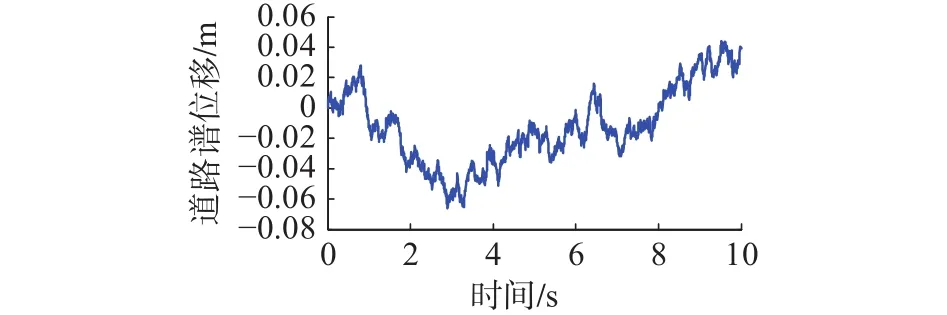
图3 60 km/h 车速下 C 级道路谱时域位移信号
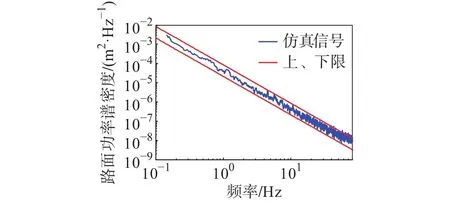
图4 60 km/h 车速下 C 级道路谱的功率谱信号
1.3 1/4悬架系统仿真系统模型
车辆在行驶中,汽车左右运动对称时且质量分配系数接近1时,前后悬架的振动几乎独立,此时可以将前后悬架分开建模,于是就可以通过单轮二自由度系统对整个悬架的振动情况进行模拟,此时只需考虑簧载质量与非簧载质量的垂直振动[15]。
某越野车的前悬架为双摆臂扭杆弹簧独立悬架,因此车辆左右振动独立,且由于该车的质量分配系数接近1,因此采用单轮二自由度系统对车辆的振动性能进行仿真研究,系统动力学模型见图5所示。
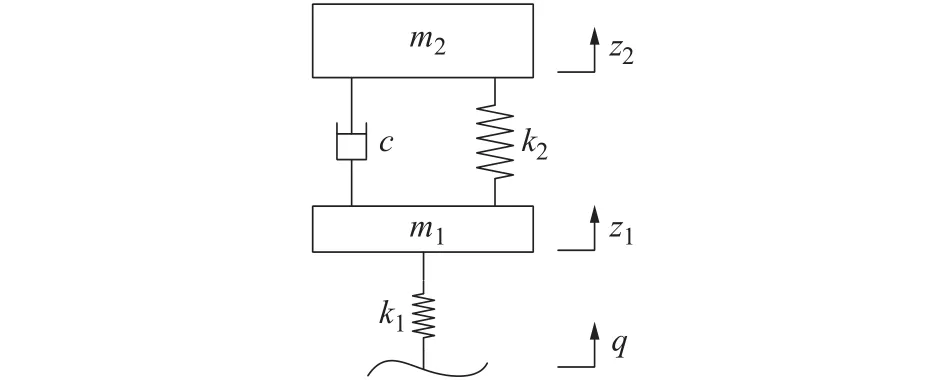
图5 二自由度系统动力学模型
根据图5的二自由度系统动力学模型发现该模型可以由具有黏性阻尼的二自由度系统受迫振动方程来表示,即:
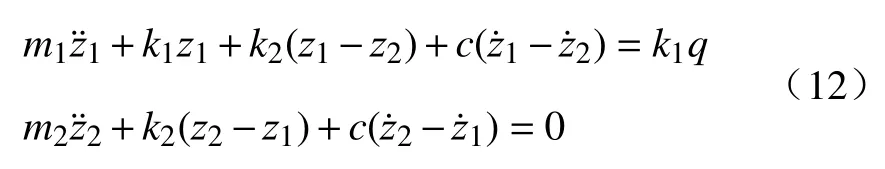
式中:m1、m2分别为车轮和悬架质量;z1、z2分别为车轮和悬架的绝对位移;q为激励位移;k1、k2分别为车轮和悬架的弹簧刚度;c为悬架阻尼系数。
2 1/4 悬架系统模型修正
由于所搭建得试验平台悬架参数未知,为建立准确的被动悬架仿真模型需要根据振动试验采集的卸下磁流变阻尼器的试验平台振动响应对仿真模型的刚度与阻尼系数进行辨识,结合阻尼器出力模型建立磁流变半主动悬架系统动力学仿真模型,根据采集的安装磁流变阻尼器的试验平台振动响应对该模型进行修正,修正流程如图6所示。
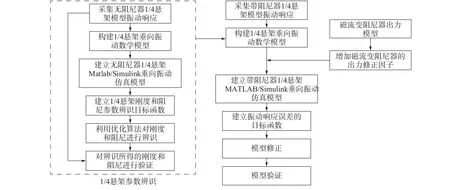
图6 1/4 悬架动力学仿真模型修正流程
2.1 遗传算法
遗传算法以进化论优胜劣汰为基本原理的一种全局优化算法。通过如图7所示得遗传算法对模型进参数辨识与模型修正。
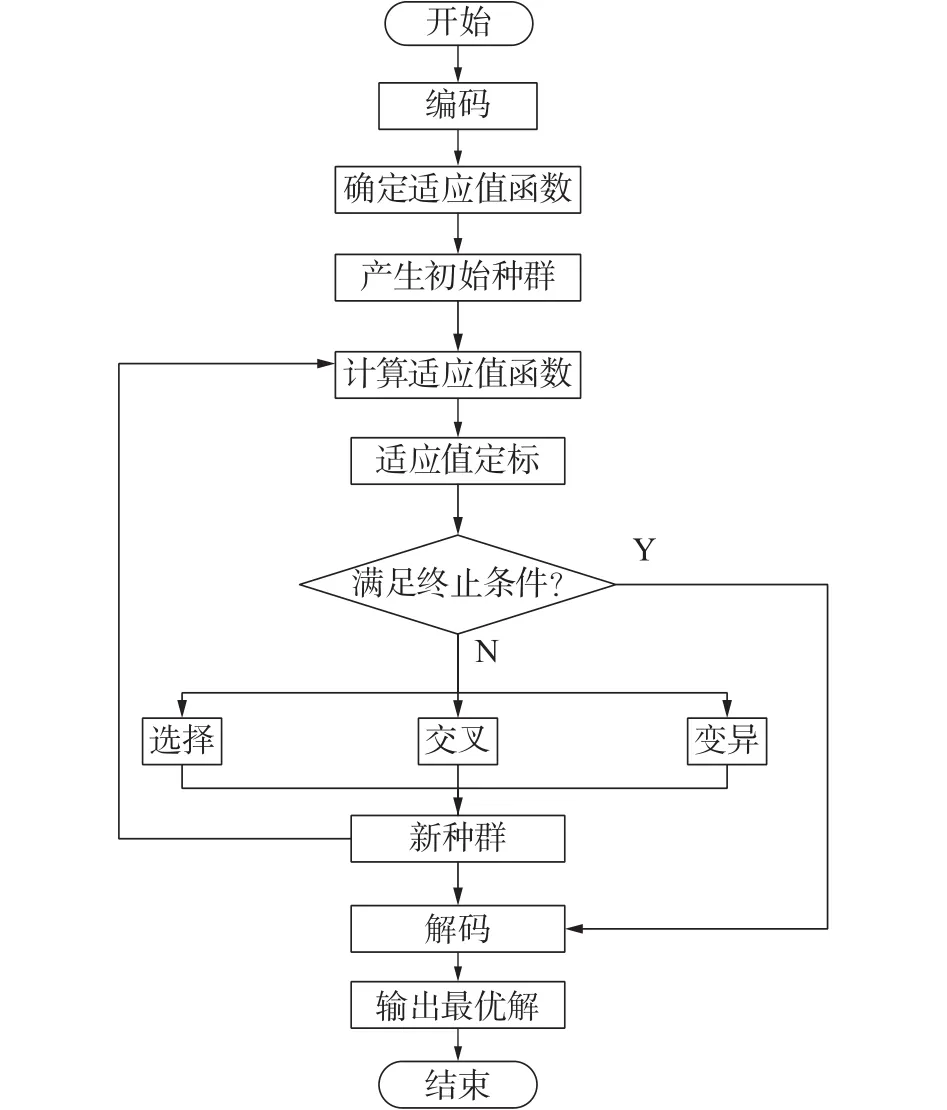
图7 遗传算法流程图
2.2 1/4悬架振动试验
首先根据仿真模型搭建如图8所示1/4悬架垂向振动试验平台,然后通过振动台给1/4悬架模型加载位移或加速度激励。通过oros信号采集仪与加速度传感器采集到的振动响应信号。

图8 试验现场图
2.3 被动悬架参数辨识
安装阻尼器前,理论上来说在1/4悬架缩比模型中只存在刚度而不存在阻尼,但考虑到实际中试验平台存在的结构阻尼,所以可根据图5所示的1/4悬架动力学仿真模型对悬架的仿真参数进行辨识,使仿真得到的系统响应与试验采集得到的数据一致。
根据动力学方程在MATLAB/Simulink中搭建1/4悬架振动仿真模型,其中将参数k1、k2、c设置为变量。将初始种群中的变量参数代入Simulink进行仿真并通过导入的实验数据计算适应度函数并判断是否满足停止条件,若满足则输出该变量,若不满足通过选择、交叉与变异形成新的种群然后反复迭代知道满足条件。
在MATLAB/Simulink中建立二自由度系统仿真模型,通过遗传算法修正k1、k2、c,使仿真得到的响应与试验响应误差最小。给1/4悬架仿真模型施加一个正弦位移激励,通过迭代悬架参数并将仿真响应与相同激励的正弦振动试验采集得到的响应数据做差得到目标函数进行辨识得到悬架参数。不同频率幅值的正弦试验下的辨识结果见表2。

表2 正弦激励辨识结果
给1/4悬架仿真模型施加一个道路谱激励,通过迭代悬架参数并将仿真响应与相同激励的道路谱振动试验采集得到的响应数据做差得到目标函数进行辨识得到悬架参数。不同车速与不平度等级的道路谱激励下的辨识结果如表3所示。

表3 道路谱激励辨识结果
根据表2与表3的辨识结果选取合适的悬架参数:k1= 103.3 kN/m,k2= 19.1 kN/m,c= 189.9 N·s/m。
将选取的悬架参数代入到在频率为3 Hz振幅为3.5 mm的正弦激励下的动力学仿真中,试验与仿真的加速度响应对比如图9所示。
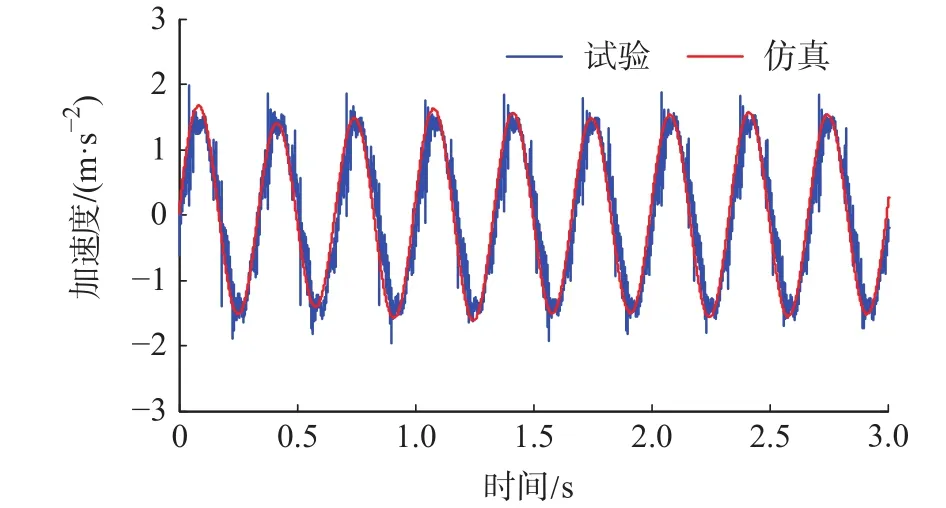
图9 正弦激励下的修正模型与试验对比
将选取的悬架参数代入到车速为60 km/h的C级路面不平度道路谱激励下的动力学仿真中,试验与仿真的加速度响应对比如图10所示。
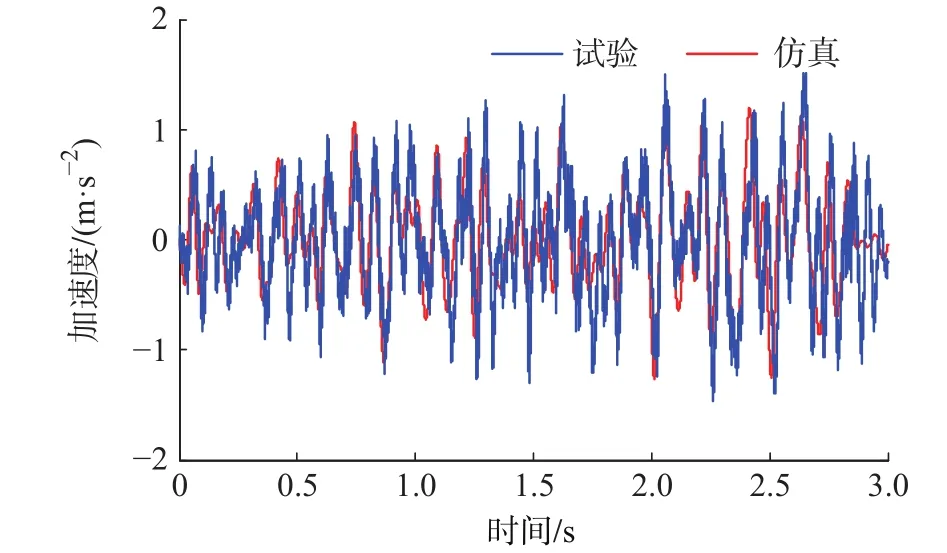
图10 道路谱激励下的修正模型与试验对比
通过图9和图10可知,将辨识得到的悬架参数代入到仿真模型中,无论在在正弦激励还是在道路谱激励下仿真得到的系统响应数据与试验采集得到响应数据基本吻合,因此通过该辨识结果得到的仿真模型仿真得到的响应数据能够模拟真实的1/4悬架的响应信号。
对图10中实验与仿真的悬架振动响应数据进行频谱分析,得到其幅频曲线对比图,如图11所示。
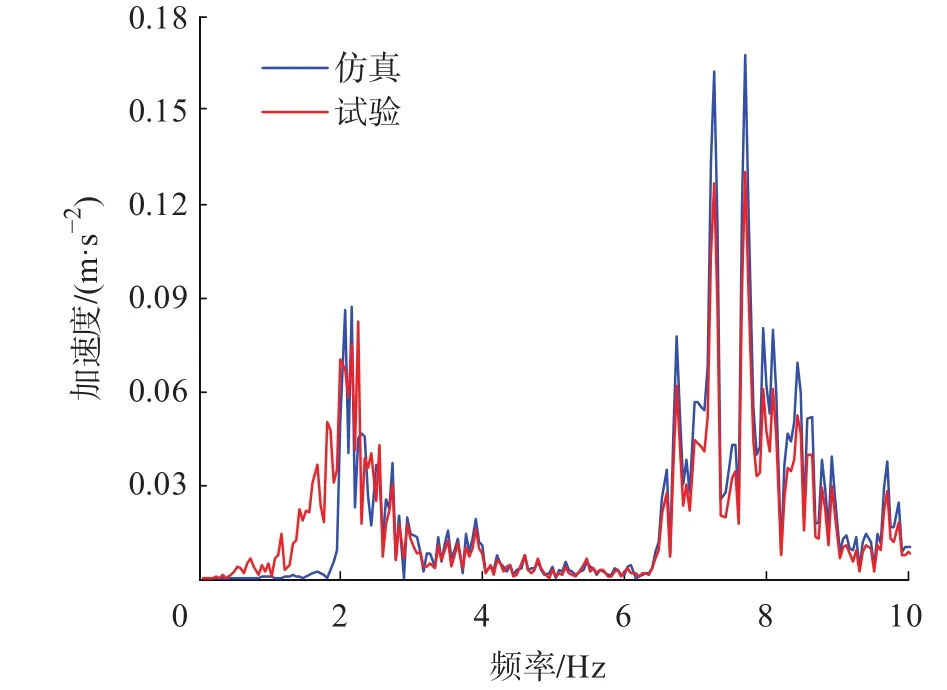
图11 试验与仿真响应的幅频曲线
根据图11可以发现辨识得到的悬架模型与试验模型的两阶固有频率一致,且在相同激励下,其幅频曲线较为吻合,因此能证明该辨识结果的准确性。
2.4 磁流变半主动悬架系统模型修正
根据磁流变液串联本构模型建立的阻尼器出力模型可以表示为
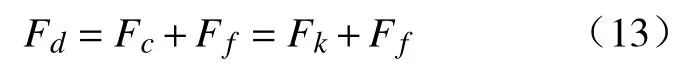
式中:Fc=Fμ+Fτ,Fμ为黏滞阻尼力,Fτ为库伦阻尼力。
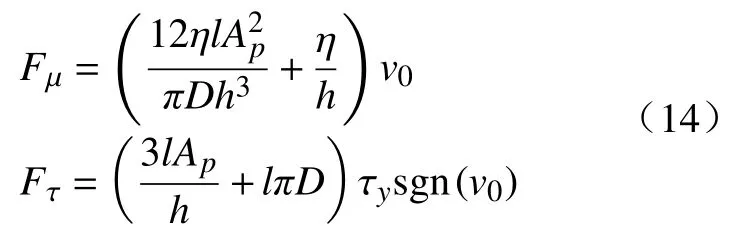
将阻尼器模型加入到被动悬架仿真模型中建立1/4磁流变半主动悬架系统动力学仿真模型,该模型如图12所示。
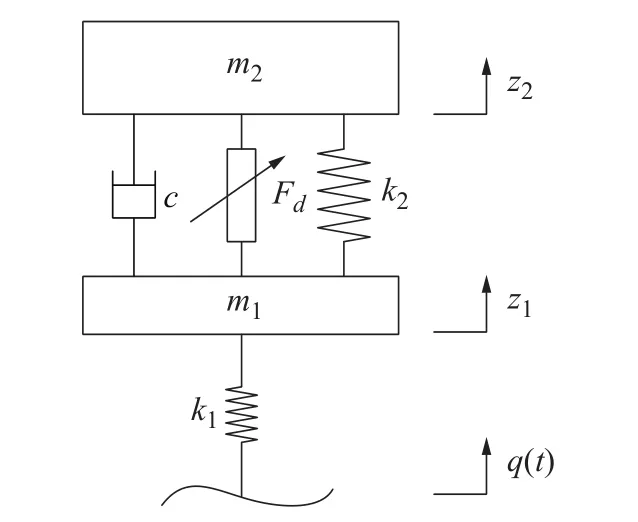
图12 有阻尼器 1/4 悬架修正模型
其动力学方程为:

但是由于仿真模型与实际阻尼器出力存在一定的误差,为建立准确的磁流变半主动悬架系统仿真模型需要对公式(13)中的阻尼器出力进行修正。为此在磁流变阻尼器出力模型中添加一组修正因子{α1,α2,α3,α4},此时的阻尼器出力模型为

通过遗传算法对修正因子{α1,α2,α3,α4}在全局寻优,得到仿真响应与实验响应误差最小时的修正因子。给安装磁流变阻尼器的1/4悬架仿真模型施加一个正弦位移激励,通过迭代修正因子并将仿真响应与相同激励下的正弦振动实验采集得到的响应数据做差得到目标函数进行修正得到修正后的修正因子。不同频率幅值的正弦试验修正结果见表4。
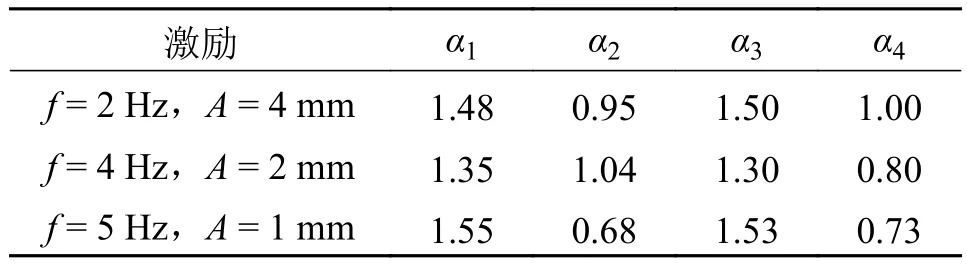
表4 正弦激励修正结果
给安装磁流变阻尼器的1/4悬架仿真模型施加一个道路谱激励,通过迭代修正因子并将仿真响应与相同激励下的道路谱振动实验采集得到的响应数据做差得到目标函数进行修正得到修正后的修正因子。不同车速与不平度等级的道路谱激励下的修正结果见表5。
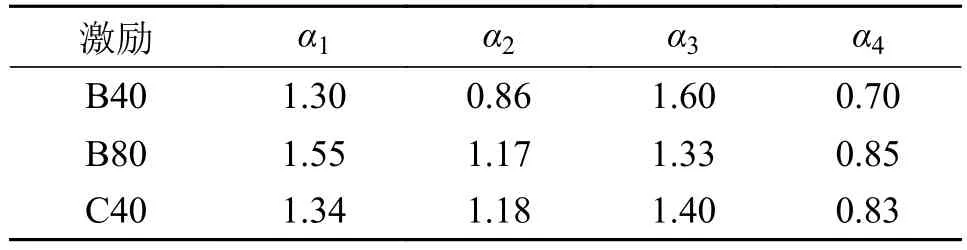
表5 道路谱激励修正结果
根据表4与表5的修正结果选取合适的悬架参数,α1= 1.43,α2= 0.98,α3= 1.44,α4= 0.82。
将选取的阻尼器修正因子代入频率为3 Hz振幅为3.5 mm的正弦激励下的动力学仿真中,试验与仿真的加速度响应对比如图13所示。
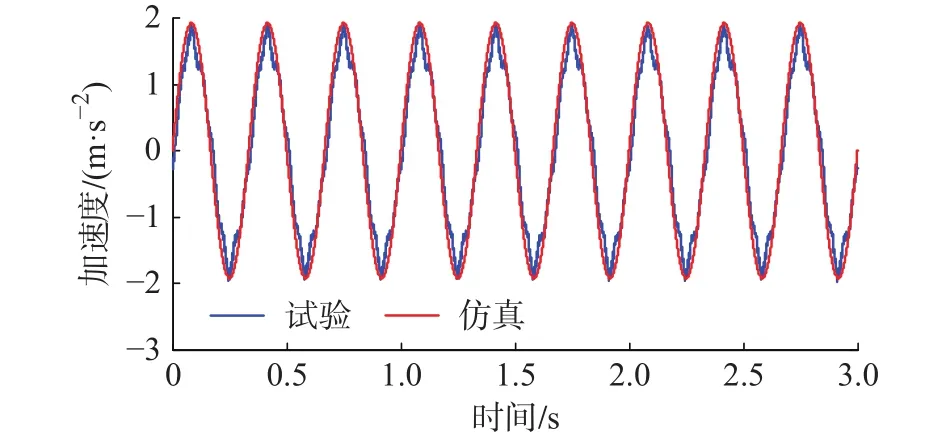
图13 正弦激励下的修正模型与试验对比
将选取的阻尼器修正因子代入C级路面不平度车速为60 km/h的道路谱激励下的动力学仿真中,实验与仿真的加速度响应对比如图14所示。
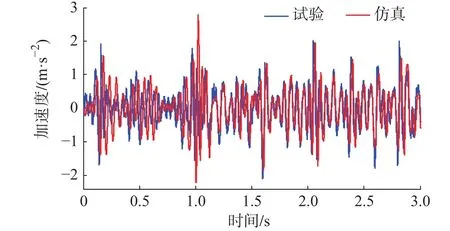
图14 道路谱激励下的修正模型与试验对比
通过图13和图14可知,在正弦激励以及道路谱激励下修正后的仿真模型仿真得到的系统响应数据与实验采集得到响应数据吻合,因此该修正后的仿真模型仿真得到的响应数据能够模拟真实带磁流变阻尼器的1/4悬架的响应信号。
对图14中试验与仿真的悬架振动响应数据进行频谱分析,得到其幅频曲线对比图,如图15所示。
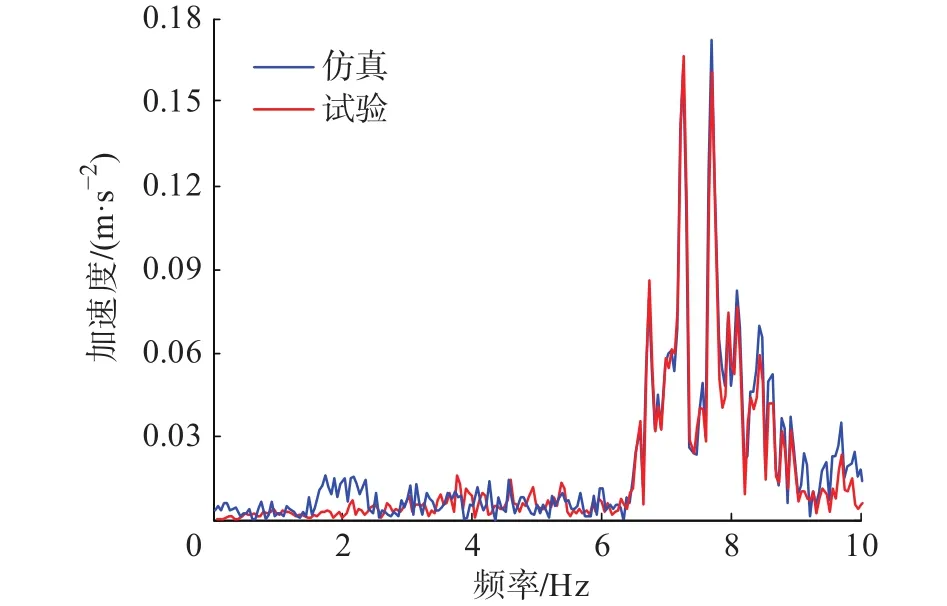
图15 试验与仿真响应的幅频曲线
根据图15可以发现修正得到的悬架模型与试验模型的两阶固有频率一致,且在相同激励下,其幅频曲线较为吻合,因此能证明该修正模型的准确性。
3 阻尼器结构对振动响应影响
结合上述得到的辨识结果,建立以结构参数为变量的磁流变阻尼器出力模型,并将其代入到1/4悬架动力学仿真模型中。仿真得到不同结构参数下的悬架动力学响应,并分析得到悬架响应与结构参数之间的规律。
3.1 悬架性能评价指标
悬架性能的优劣决定着汽车运行的平顺性以及操纵的稳定性,因此可以通过汽车行驶时的平顺性与车辆操纵的稳定性来对悬架的性能进行评价。
在ISO2631-1:1997(en)[16]标准中对车身加速度评价汽车平顺性作出明确的规定:当车身垂向加速度的峰值系数小于9(峰值系数定义为:加权加速度的时间历程的峰值和加速度均方根值的比值)时,可以通过加权之后的加速度均方根值来评价汽车的平顺性。该方法适用于各种行驶在正常道路上的车辆。
加权加速度均方根值 (m/s2) 为

aw(t)为计权加速度,其中车体加速度加权函数wa(f)可以参照 ISO 2361-1:1997(en),其取值为:
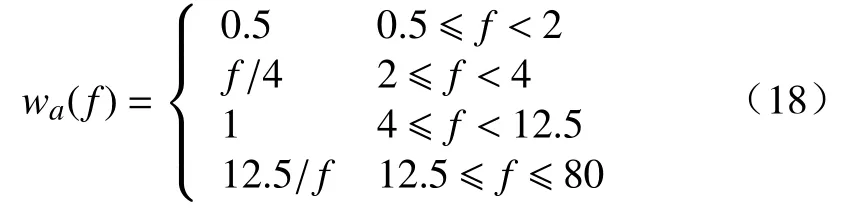
轮胎动载荷[17]是车辆在行驶过程中轮胎在垂直方向产生的作用力与垂直方向静载荷(车辆静止时轮胎在垂直方向产生的作用力)的差值。当轮胎静载荷小于轮胎动载荷时,此时车轮的静变形小于动变形那么此时车轮将离开地面从而丧失附着能力,此时汽车的安全性与操纵的稳定性变差。另外,当车轮动载荷过大时,此时轮胎与地面的接触面变大会增加车辆行驶时的阻力,因此会对车辆行驶性能造成影响并加剧轮胎的磨损。所以轮胎的动载荷可以作为评价悬架性能的一个评价标准。
3.2 结构参数对振动响应影响分析
1)正弦激励下阻尼器结构参数对振动响应的影响
通过仿真比较频率为2 Hz振幅,为4 mm的正弦位移激励下阻尼器结构参数的变化对1/4悬架系统响应的影响。
通过图16和图17发现,在频率为2 Hz,振幅为4 mm的正弦位移激励下悬架系统加权加速度均方根值与动载荷均方根值都随阻尼间隙的增大而增大,且都随着活塞有效长度、活塞直径与活塞杆直径的增大而减小。其中随着阻尼间隙从初始值的0.5倍增大到1.5倍时加权加速度均方根值最大值与最小值的差值为 0.142 9 m/s2,动载荷均方根值的最大与最小值之差为25.777 2 N。活塞直径从初始值的0.5倍增大到1.5倍时加权加速度均方根值最大值与最小值的差值为 0.523 8 m/s2,动载荷均方根值的最大与最小值之差为88.038 3 N。而另外两个参数的加权加速度均方根值变化幅度约为0.02 m/s2,动载荷均方根值最大与最小值之间的差值皆小于5 N。因此根据各参数下加权加速度均方根值与动载荷均方根值的变化幅度可以发现正弦位移激励下阻尼间隙与活塞直径这两个参数对悬架加速度与动载荷响应的影响较大。
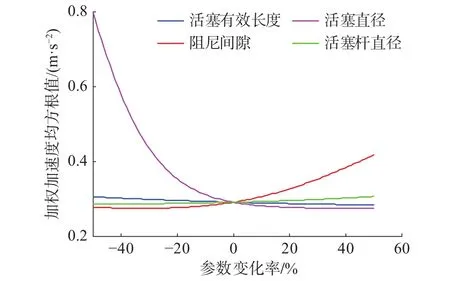
图16 正弦激励下结构参数对加权加速度均方根值的影响
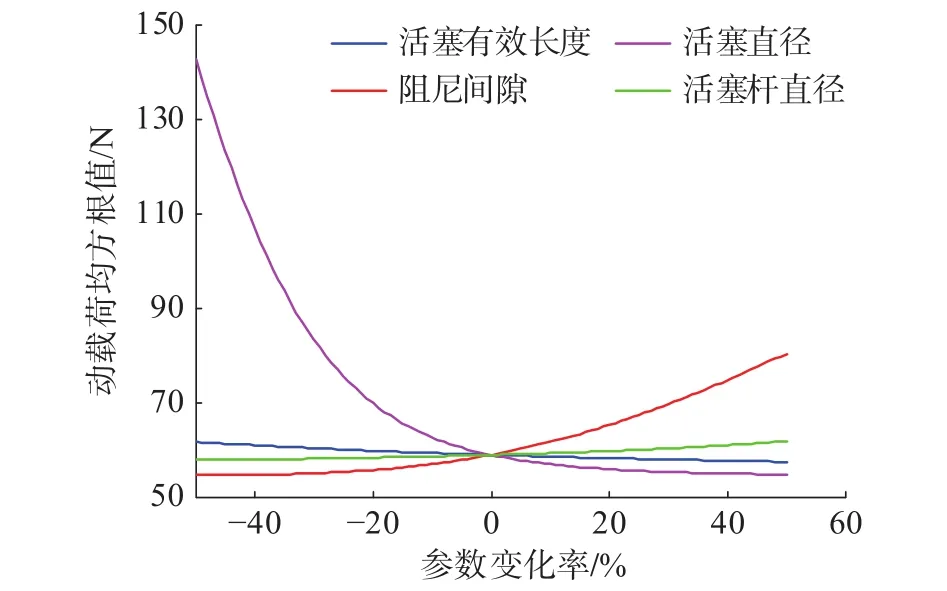
图17 正弦激励下结构参数对动载荷均方根值的影响
2)道路谱激励下阻尼器结构参数对振动响应的影响
通过仿真比较C级路面下车速为60 km/h的道路谱激励信号下阻尼器结构参数减小50%到增大50%,对1/4悬架系统响应的影响。
通过图18和图19发现,以60 km/h的车速在C级不平度等级的道路上行驶时系统加权加速度均方根值随着阻尼间隙与活塞杆直径的变大而减小,随着活塞直径与活塞有效长度的增大而增大。动载荷均方根值随阻尼间隙与活塞直径的增大都有一个先减小后增大的趋势,并且随着活塞有效长度的增大而减小,随着活塞杆直径的增大而增大。其中随着阻尼间隙从初始值的0.5倍增大到1.5倍时加权加速度均方根值最大值与最小值的差值为0.911 5 m/s2,动载荷均方根值的最大与最小值之差为36.273 5 N。活塞直径从初始值的0.5倍增大到1.5倍时加权加速度均方根值最大值与最小值的差值为0.542 4 m/s2,动载荷均方根值的最大与最小值之差为102.1481 N。而另外两个参数的加权加速度均方根值变化幅度约为0.1 m/s2,动载荷均方根值最大与最小值之间的差值皆小于14 N。因此根据各参数下加权加速度均方根值与动载荷均方根值的变化幅度可以发现道路谱激励下阻尼间隙与活塞直径这两个参数对悬架加速度与动载荷响应的影响较大。
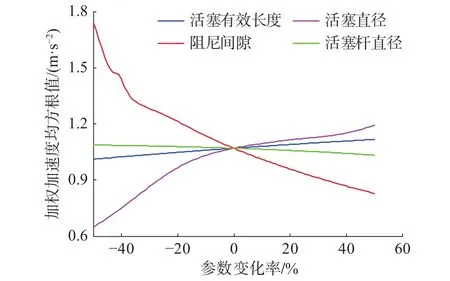
图18 道路谱激励下结构参数对加权加速度均方根值的影响
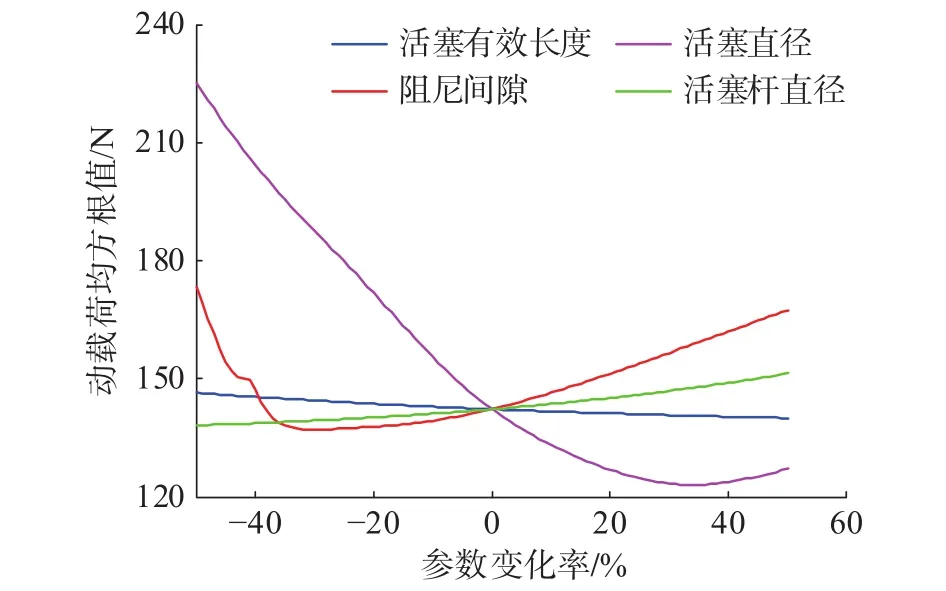
图19 道路谱激励下结构参数对动载荷均方根值的影响
3.3 影响因子分析
为定量分析阻尼器活塞有效长度l、阻尼间隙h、活塞直径D和活塞杆直径d对悬架振动响应的影响,引入一种百分比斜率均方根值的评价方法[5],其计算公式[5]为 :
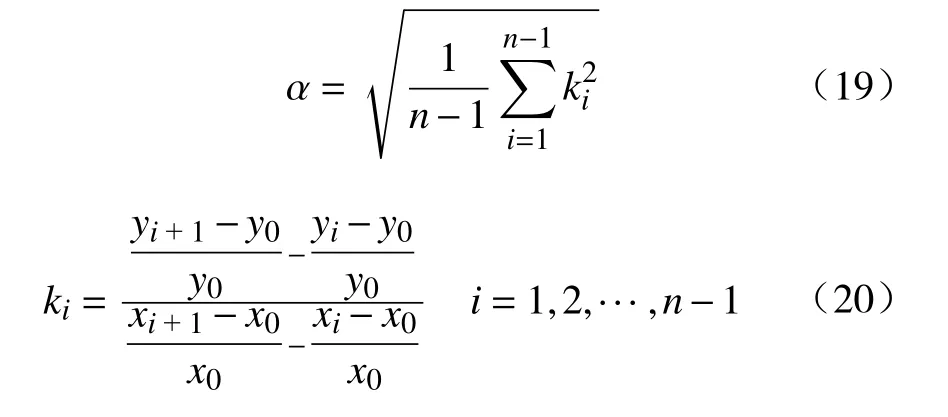
根据式(19)与式(20)可知,各结构参数对1/4悬架的车身加速度响应的影响因子如图20所示。同理,此时各结构参数对1/4悬架的车轮动载荷的影响因子如图21所示。
通过图20与图21可以发现在正弦激励下活塞直径对悬架的加速度与动载荷影响因子最大,车身加速度影响因子达到1.2875,动载荷影响因子达到1.0727。而阻尼间隙的车身加速度影响因子为0.5037,动载荷影响因子为0.4504,而其余两个参数的加速度与动载荷影响因子都小于0.1。在道路谱激励下活塞直径对悬架的动载荷影响因子最大而阻尼间隙对车身加速度影响因子最大。活塞直径的车身加速度影响因子为 0.4379,动载荷影响因子达到0.8104。而阻尼间隙的车身加速度影响因子达到0.6355,动载荷影响因子为0.2621,而其余两个参数的加速度与动载荷影响因子都小于0.1。
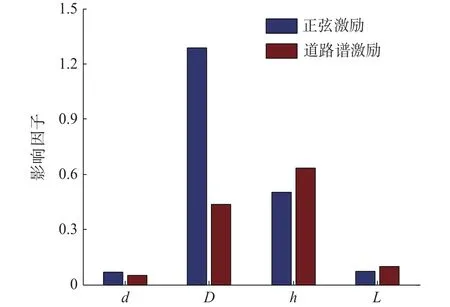
图20 车身加速度影响因子
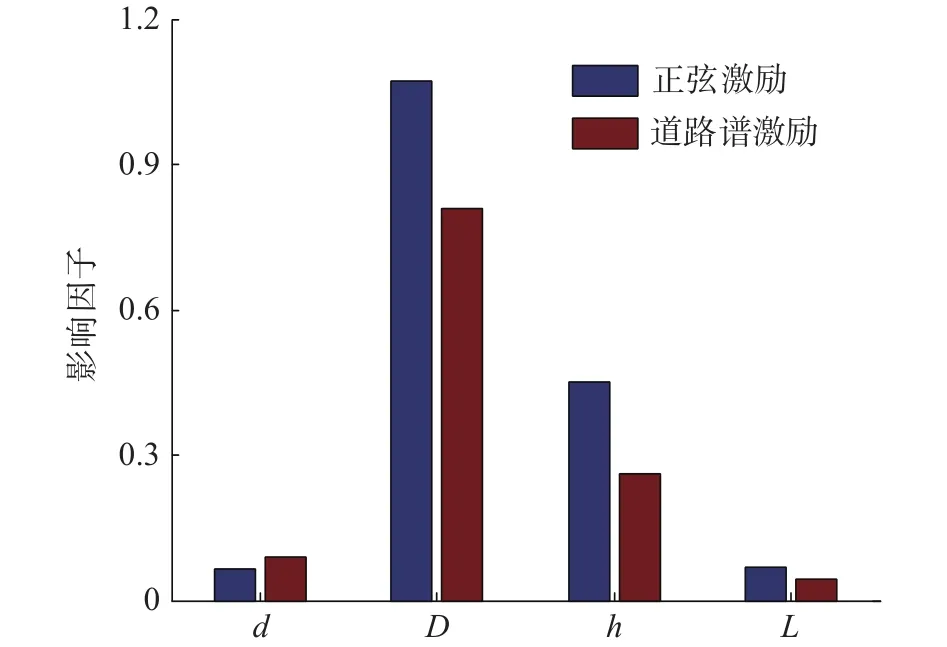
图21 车轮动载荷影响因子
因此可以说明阻尼器的各结构参数中活塞直径与阻尼间隙这两个参数对车身加速度响应与车轮动载荷的影响要比其它参数的大的多。
4 结论
1)根据采集得到的安装磁流变阻尼器前的悬架模型振动实验响应数据对被动悬架系统仿真模型中的悬架参数进行辨识,根据时域与幅频分析发现根据辨识得到的悬架参数建立的仿真模型,其仿真与实验信号较为吻合。
2)根据采集得到的安装磁流变阻尼器后的悬架模型振动实验响应数据对磁流变悬架系统仿真模型进行模型修正,根据时域与幅频分析发现根据修正后的仿真模型,其仿真与实验信号较为吻合。
3)根据修正后的磁流变悬架动力学模型分析了阻尼器各结构参数对悬架减振性能的影响,得到阻尼器的阻尼间隙与活塞直径对悬架减振性能影响较大。
