巧同构 妙分离——一道不等式恒成立题的破解

福建省莆田第一中学（351100） 林 敏

含参不等式恒成立问题是高中数学学习的一大重点，它往往综合函数、不等式、方程等相关知识，注重考查数学运算、逻辑推理等素养，以及函数与方程思想、化归与转化思想、分类与整合思想等。其以覆盖知识点多、综合性强、解法灵活等特点而备受命题者青睐。含参不等式恒成立问题切入点不明显，让人无从下手，破解的实质是结合题目条件对恒成立不等式进行等价转化，合理转化为熟悉的不等式、函数或方程问题后，根据相应的不等式、函数或方程问题来分析与处理。

一、题目呈现

【题目】（清华大学2020年1月中学生标准学术能力诊断性测试文科数学试卷第12 题）已知不等式x+alnx+≥xa对x∈(1,+∞)恒成立，则实数a的最小值为（ ）。

二、题目解析

此题涉及指数、对数、幂混合型函数所对应的不等式恒成立，在此条件下确定对应参数的取值范围问题。知识融合度大，能力要求多，题目难度大，对考生的数学基本知识、数学思想方法和数学能力等各方面的要求比较高。

该题背景创新，设计新颖，把指数、对数、幂函数这三类基本初等函数加以巧妙融合，综合不等式恒成立这一个热点加以合理构造，把函数、方程、不等式等知识有机交汇，借助代数运算、不等式性质、函数与导数等相关方法来转化与处理，充分体现高考在知识交汇处命题的指导思想。

在具体破解题目时，可以结合参数的不同取值情况进行分类讨论，也可以利用同构函数或重要结论，运用分离参数法分析与处理。合理化归与转化，实现相应函数最值问题的确定，进而得以求解相关参数的取值问题。

三、问题破解

方法1：分类讨论法

解析：由x+alnx+≥xa，可 得x+e-x≥xaalnx，即e-x-ln e-x≥xa-lnxa，

设函数f(t)=t-lnt，t∈(0,+∞)，

所以e-x-ln e-x≥xa-lnxa等价于f(e-x)≥f(xa)，x∈(1,+∞)，

而f′(t)=1-，由f′(t)=0可得t=1，

则知函数f(t)在（0，1）上单调递减，在(1,+∞)上单调递增，

所以f(t)min=f(1)=1，

而x∈(1,+∞)，则有0 ＜e-x＜e-1=

（1）当a=0 时，xa=1，不等式f(e-x)≥f(xa)恒成立，因而a的最小值小于等于0；

（2）当a＜0时，0 ＜xa＜1，

而0 ＜e-x＜1，f(t)在（0，1）上单调递减，

由f(e-x)≥f(xa)，可得e-x≤xa，整理可得-x≤alnx，则有a≥

设函数g(x)=，x∈(1,+∞)，求导有g′(x)=，由g′(x)=0可得x=e，

当x∈(1,e) 时，g′(x) ＞0，g(x) 单调递增；当x∈(e,+∞)时，g′(x) ＜0，g(x)单调递减；

所以g(x)max=g(e)=-e，即a≥-e，亦即实数a的最小值为-e，故选C。

点评：对题目中恒成立的不等式加以等价变形，构造函数f(t)=t-lnt，通过求导并分析函数单调性与确定最值，再对参数a进行分类讨论以及深入分析函数的单调性，得到不等式-x≤alnx恒成立，进而通过分离参数，并结合函数的构造，以及函数的单调性与最值的求解来确定参数的取值范围。这里分离参数的方式多样，还可以分离为≥-a或等不同形式，都能达到目的。

方法2：同构+分离参数法

解析：由x+alnx+≥xa，可得x+e-x≥xa-alnx，即x+e-x≥xa+lnx-a，

设函数f(x)=x+e-x，x∈(1,+∞)，则f(lnx-a)=lnx-a+e-lnx-a=lnx-a+xa，

所以x+e-x≥xa+lnx-a等价于f(x) ≥f(lnx-a)，

而f′(x)=1-e-x＞0，则函数f(x)在区间(1,+∞)上单调递增，

所以x≥lnx-a=-alnx，分离参数可得a≥

设函数g(x)=，x∈(1,+∞)，则g′(x)=

令g′(x)=0，解得x=e，

当x∈(1,e) 时，g′(x) ＞0，g(x) 单调递增；当x∈(e,+∞)时，g′(x) ＜0，g(x)单调递减；

所以g(x)max=g(e)=-e，即a≥-e，亦即实数a的最小值为-e，故选C。

点评：对题目中恒成立的不等式加以等价变形，使得不等号两边呈现出形式完全一样的函数结构，利用函数f(x)=x+e-x进行同构处理，并深入分析函数的单调性，得到不等式x≥-alnx恒成立，进而通过分离参数，并结合函数的构造，以及函数的单调性与最值的求解来确定参数的取值范围。

方法3：结论+分离参数法

解析：由x+alnx+≥xa，可 得x+alnx+≥elnxa，即x·ex+a·exlnx+1 ≥ex·elnxa，

整理可得x·ex+a·exlnx+1 ≥ex+alnx，

根据重要结论“ex≥x+1，当且仅当x=0时等号成立”，可得ex+alnx≥x+alnx+1，当且仅当x+alnx=0时等号成立，

则有x·ex+a·exlnx+1 ≥ex+alnx≥x+alnx+1，整理可得alnx(ex-1) ≥x(1-ex)，

而x∈(1,+∞)，则有ex-1 ＞0，lnx＞0，

则有alnx≥-x，分离参数可得a≥

设函数g(x)=，x∈(1,+∞)，则g′(x)=

令g′(x)=0，解得x=e，

当x∈(1,e) 时，g′(x) ＞0，g(x) 单调递增；当x∈(e,+∞)时，g′(x) ＜0，g(x)单调递减；

所以g(x)max=g(e)=-e，即a≥-e，亦即实数a的最小值为-e，故选C。

点评：对题目中恒成立的不等式加以等价变形，根据重要结论“ex≥x+1”加以过渡与转化，结合不等式的基本性质加以变形与分析，得到不等式x≥-alnx恒成立，进而通过分离参数，并结合函数的构造，以及函数的单调性与最值的求解来确定参数的取值范围。

四、变式拓展

探究1：保留题目所有条件，改变问题的设问方式，改原来确定“实数a的最小值”为确定“实数a的取值范围”，从另一个角度来合理设问，得到以下对应的变式问题。

变式1：已知不等式x+alnx+≥xa对x∈(1,+∞)恒成立，则实数a的取值范围为（ ）。

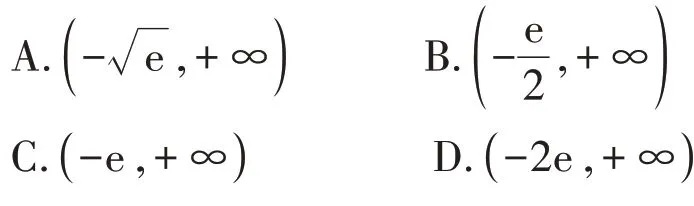
答案：C。该问题的具体解析过程与原问题的解析过程一致，这里就不多加以叙述。

探究2：保留题目的创新情境，改变条件中恒成立的不等式的给出方式，以类似的不等式形式来加以变式与拓展，得到以下相应的变式问题。考查的知识点、能力点以及试题难度基本相当。

变式2：已知不等式eax+lnx≥(a+1)x对x∈(1,+∞)恒成立，则正实数a的最小值为（ ）。

解析：函数y=ex-x在(0,+∞)上为增函数，而原不等式即为eax-ax≥x-lnx=elnx-lnx，则知ax≥lnx，即a≥

令函数h(x)=，则h′(x)=

令h′(x) ＞0，解得0 ＜x＜e；令h′(x) ＜0，解得x＞e，

故函数h(x)在区间(0,e)上单调递增，在区间(e,+∞)上单调递减，

所以函数h(x)的最大值是h(e)=，即a≥故选A。

探究3：保留题目的创新情境，从另一个层面改变恒成立的不等式的给出方式，进而确定参数的取值范围，得到以下对应的变式问题。考查的知识点、能力点以及试题难度基本相当。

变式3：已知关于x的不等式-x-alnx≥1对于任意x∈(1,+∞)恒成立，则实数a的取值范围为（ ）。

A.(-∞,1-e] B.(-∞,-3]

C.(-∞,-2] D.(-∞,2-e2]

解析：由题意可知，分离参数a≤令函数f(x)=

由题意可知a≤f(x)min，由于f(x)=

又因为重要不等式ex-1 ≥x，当且仅当x=0时等号成立，

所以f(x)=当且仅当x-3lnx=0时等号成立，

所以函数h(x)的最大值是h(e)=方程有解，a≤-3，故选B。

五、解后反思

解决含参不等式恒成立问题，经常要对恒成立的不等式加以移项、恒等变换等等价变形，借助不等式左右两边呈现出形式、函数类型完全一样的状态，进而构造对应的函数，结合求导等方法来判定对应函数的单调性后再分析与解决，这就是处理此类问题的同构思维。运用同构思维法破解含参不等式恒成立问题时，关键在于突破命题者巧妙设置的原先形式明显、规划整齐的式子，而在题目条件中所显示的是打乱后重新排列的看似杂乱无章的式子，这也是问题的切入点所在，可以很好地考查学生的数学运算能力和逻辑推理能力。当然也可以借助其他思维方式来破解此类问题，无论采用哪种破解策略、何种解题方法来处理，都离不开函数与方程思想的运用，都离不开逻辑推理与数学运算，同时还需借助函数、不等式、方程之间的相互转化与应用等。