一次同课异构教研活动的思考——“等比数列的前n项和”教学点评

四川宜宾市叙州区第二中学校（644600） 康中君

一、课例呈现

第一位教师的教学简况：

1.复习回顾

（1）等比数列的定义；

（2）等比数列的通项公式。

2.情境引入

引入有关古印度舍罕王与宰相西萨·班·达依尔的国际象棋故事。

引导学生分析问题，发现问题：

由于棋盘每一格的麦粒数都是前一格的2 倍，共有64 格，则每一格所放的麦粒数依次为1,2,22,…,263，S64=1+2+22+…+263。这个算式的结果是多少呢？

3.知识讲解

探究等比数列的前n项和公式。

4.典例精讲

［例1］（1）求下列等比数列的前8项和。

（2）欣赏诗词，解答问题。

远望巍巍塔七层，红光点点倍加增，

共灯三百八十一，请问尖头几盏灯？

（3）求1+a+a2+…+an（a≠0）。

5.小结

等比数列的前n项和公式。

方法：错位相减法。

第一步，等式两边同乘公比。

第二步，错位、作差。

第三步，化简得结论。

6.作业布置

已知Sn是等比数列{an}的前n项和，S4=5S2，求的值。

第二位教师的教学简况：

1.新课引入

（文字叙述同样的国际象棋故事）

问题1：国王能实现他的诺言吗？

追问：上述问题本质上是属于数列中的什么问题？（数列求和，等比数列的前n项和）

2.概念形成

问题2：在解决等差数列的前n项和问题时，通过什么方法来实现运算方式的转化？最后运算简化到什么程度？

问题3：求等比数列的前n项和时，你希望通过运算方式的转化后把运算简化到什么程度呢？

简化到只要给出首项a1，末项an或者公比q，以及项数n，即可求和。

问题4：求等比数列的前n项和时，你能否找到一种方法来转化运算方式，从而简化运算？

追问1：等式右边求和运算困难的原因是什么？（省略号的存在，项太多）

追问2：等式右边的项太多，怎样才能使其变少？（转化运算方式，消项）

追问3：观察等式右边，任意相邻两项之间有什么关系？（前一项乘以q得后一项）

追问4：只要找到相同的项作差就能消项，怎样才能找到相同的项？

3.概念深化

问题5：在消项的过程中，等式两边必须乘以公比q吗？（可同乘以

问题6：等比数列前n项和Sn与前n-1 项和Sn-1有什么关系？

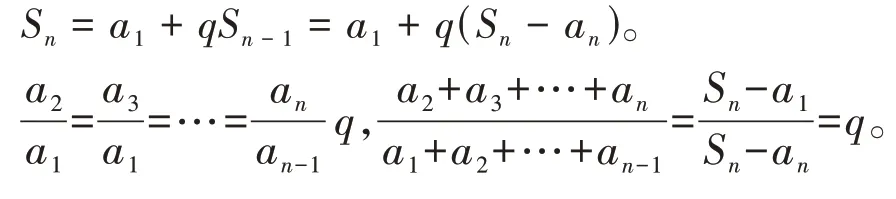
等比数列的前n项和公式：

问题7：你能通过等比数列的前n项和公式求出国王应该赏赐的麦粒数吗？

注意：

（1）q=1与q≠1两种情况；

（2）公式Sn=有4个量；

（3）n是项数而非指数。

4.应用探索

［例1］同第一位教师应用的例1。

［例2］某商场今年销售计算机5000 台。如果平均每年的销售量比上一年的销售量增加10%，那么从今年起，大约几年可使总销售量达到30 000台？（结果保留到个位）

［例3］如图1，为了估计函数y=9-x2在第一象限的图像与x轴，y轴围成的区域的面积X，把x轴上的区域[ ]0,3 分成n等分，从各分点作y轴的平行线与函数图像相交，再从各交点向左作x轴的平行线，构成（n-1）个矩形，下面的程序用来计算这（n-1）个矩形的面积的和S。

图1

（1）程序中的AN，SUM 分别表示什么？为什么？

（AN 表示第k个矩形的面积；SUM 表示前k个矩形的面积的和。）

（2）请根据程序分别计算当n=6,11,16 时，各个矩形的面积的和。

5.小结

问题8：这节课主要学习了什么内容？

（1）“错位相减法”在简化运算时的操作方法；

（2）用“错位相减法”推导出等比数列的前n项和公式；

（3）等比数列的前n项和公式的两种形式；

（4）计算机循环结构可用于数列描述，也可用于数列求和；

（5）数学方程思想，无限逼近的思想。

二、课例对比

（一）课堂结构相同

两位教师都是采用“情境引入课题、推导公式、应用知识、课堂小结、布置作业”这样的教学流程。作为常规课例展示，这样的安排没有特别出彩，中规中矩。学生能在情境中抽象出数学概念，积累从具体到抽象的活动经验。情境引入后的问题分析，可以认为是发现问题，S64=1+2+22+…+263这个算式的结果是多少？是提出问题，推导结果的过程是分析问题，得到求和公式再回归问题本身是解决问题。这里展示了“四能”要求，对学生的数学学习是一种示范。用故事引入，可能是很多教师的首选。但是，从“能运用等差数列、等比数列解决简单的实际问题和数学问题，感受数学模型的现实意义与应用”来看，也可以选择如储蓄方面的例子。

（二）内容大同小异

两位教师在教材内容选择上基本相同，只是对例题的使用思考不同。第一位教师只选择了例1，第二位教师选择了例1，一句话带过例2，重点探究例3。新课标要求“领会教材的编写意图及编写特点，体悟教材的呈现方式、教学价值及评价功能，在此基础上，根据不同的内容、学习任务和课型，结合自身特点和学生学习行为及现状的差异性，对教材进行有必要的重构”。结合学生实际，本节课在推导公式之后，注重求和公式的应用，结合等比数列通项公式，扎实进行基本量的计算才是重点要做的工作。例3 对数列求和有体现，但并非等比数列求和；例3 的呈现包含了程序，这是学生没有接触过的内容，因此对例3的使用要有变化；例3展示了求曲边三角形面积的一种思想——极限思想，高一学生理解有难度，需要教师想办法展现数学知识、方法和思想与实践应用的紧密联系。根据新课标“在教学中要充分体现数学来源于实际、应用于实际，突出数学的综合性和应用性”。如果不用例3，而用例2会更好。

（三）措施基本相同

两位教师都使用课件，都有学生动手、师生互动。在公式的推导过程中，第一位教师使用了视频，学生通过观看视频进行学习，有新奇性。为了直观展示例3 中n的变化发现面积特点，第二位教师用了一个图形程序。新课标强调，课堂要充分有效地运用图表、模型等教具、学具，增加直观性，根据学生的学习需要适度使用现代教育技术，提高课堂教学效率。在学法方面，引导学生主动思考、积极提问和实践探究，促进学生思维发展，激发学生的创新意识，两位教师都做得很好，都详细讲解了例1 的第②小题。笔者认为还是要求学生自己完成或合作完成比较好。

（四）教学过程有差别

两位教师的课堂结构、教学内容选择基本相同，教学过程有差别，主要反映在课堂推进方面，这里只对比公式的推导。第一位教师基本是教材的原装呈现，在树立“用教材教而不是教教材”观念方面做得不够。第二位教师通过问题2到问题6以及4 个追问使得概念的生成、公式的推导非常精彩。这样显然有利于促进学生善于观察、大胆猜想、严密思考，形成良好的数学学习习惯，有利于提升学生的数学关键能力和数学素养。

要提升学生的数学关键能力和数学素养，教师就要在教材的基础上，挖掘素材内涵，从多角度、多层次进行观察、思考，无论是解决问题的多种方法展示，还是展示解决问题的思维方式，都要精心设计。设问、追问也是培养学生数学学习方法、思维方式和思维习惯的好方式，第二位教师在这些方面做得比较好。

（五）目标达成有异

《普通高中数学课程标准（2017 年版2020 年修订）》对“等比数列”做了如下描述：

（1）通过生活实例，理解等比数列的概念和通项公式的意义。

（2）探索并掌握等比数列前n项和公式，理解等比数列的通项公式与前n项和公式的关系。

（3）能在具体的问题情境中发现数列的等比关系，并解决问题。

（4）体会等比数列与指数函数的关系。

从“探索并掌握等比数列前n项和公式”来看，两位教师都探索了公式的推导，学生掌握等比数列前n项和公式的应用，也有例题、练习和作业支撑。第一位教师用了“灯塔”一例，既应用了等比数列前n项和公式，又是对中华文化的一次展示，可以培养学生的文化自信，非常不错。但是第一位教师没有深层次展示等比数列的通项公式与前n项和公式的关系，第二位教师在这方面就做得很好。数学学科核心素养是数学课程目标的集中体现。第二位教师通过多种转化推导出等比数列前n项和公式，很好地突破了本节的难点，增加了思维量，对学生理性思维的培养有极大的帮助。相比较而言，第一位教师在数学学科核心素养的培养方面稍显不足。

三、教学反思

《普通高中数学课程标准（2017 年版2020 年修订）》中指出，情境创设和问题设计要有利于发展数学学科核心素养；数学文化应融入数学教学活动；既要重视教，又要重视学，促进学生学会学习；重视信息技术的运用，实现信息技术与数学课程的深度融合。《四川省普通高中数学学科课堂教学基本要求》明确要求融入思想方法。要做到这些，教师要深入领悟课程标准，积极积累数学素材，采众家之长为己所用。

认真备课是确保课堂教学成功的首要环节。备课要思考：预习什么内容？预习时做哪些题目？要达到什么预习效果？如何确定教学目标？采用什么样的学法和教法？如何有效实现教学目标？引入情境如何有效提出问题？如何体现数学来源于实际生活？如何包含数学文化？如何体现数学的核心价值？要开展什么教学活动，这些活动如何体现学生自主学习？要培养哪些核心素养，如何落实这些核心素养？如何组织语言精练表达？教学内容的选择怎样符合学生实际？如何实现知识应用？如何体现数学思想方法？采用什么方式检查学习效果？如何优化作业设计？如何进行学困生辅导？怎样实施课堂评价与课后评价？

总之，在育人方式改革的浪潮中，我们还在路上。