学科育人视角下的数学课例评析——以“抛物线及标准方程”教学为例

广西南宁市第三中学（530021） 陈 康 覃俊明

抛物线是平面内到定点的距离与到定直线的距离相等的点的轨迹。这一概念反映了抛物线的几何特征。类比椭圆、双曲线标准方程的获得过程，通过建立适当的平面直角坐标系，用坐标法可以推导抛物线的标准方程。由于焦点的位置不同，抛物线标准方程的形式也不同。学生通过讨论得出焦点在不同的坐标轴上的抛物线的标准方程。通过抛物线的标准方程，可以研究抛物线的几何性质及其简单应用。这样的研究体现了研究圆锥曲线的一般过程。

如何在“抛物线及标准方程”的教学中融入“立德树人”思想，体现教学的育人功能，达到学科育人的目的？下面谈谈笔者的教学设想。

一、教学设计

（一）新课引入

展示生活中的抛物线实例，引入新课，激发学生的学习热情。

1.播放我国跳水运动员在奥运会比赛中的高台跳水视频，提问：运动员经过的轨迹是什么图形？

2.展示赵州桥图片（如图1），提问：赵州桥的桥拱是什么图形？

图1

设计意图：通过生活中的实例，吸引学生的注意力，让学生对抛物线有一个感性认识，意识到研究抛物线的必要性，体会到数学来源于生活，生活离不开数学，同时感受到中国古代文明的伟大和体育健儿在努力为国争光。

（二）概念形成

问题1：抛物线有什么样的几何性质？怎样给抛物线下定义呢？

教师：我们知道，在平面内与一个定点F(c,0)的距离和一条定直线l（其中定点F不在定直线l上）的距离的比是常数e。当0 ＜e＜1时，点的轨迹是椭圆；当e＞1 时，点的轨迹是双曲线。那么当e=1 时，即平面内与一个定点F(c,0)的距离恰好等于它到一条定直线l（其中定点F不在定直线l上）的距离的点的轨迹是什么呢？下面老师通过几何画板描出满足这样条件的点的轨迹，请大家注意观察。

设计意图：让学生对“平面内与一个定点F(c,0)的距离恰好等于它到一条定直线l（其中定点F不在定直线l上）的距离的点的轨迹”有一个感性认识。

问题2：几何画板描出的点的轨迹像是抛物线，真的是抛物线吗？为什么？你能通过求方程来证明吗？

让学生分组讨论，教师列出讨论提纲：（1）如何建立直角坐标系？（2）推出怎样的动点轨迹方程？

教师巡堂指导，然后收集几个小组的讨论结果并做投影展示。

第一组：以定点F为原点垂直于l的直线为x轴，所得方程为y2=2px+p2。

第二组：以直线l为y轴，过定点F且垂直于l的直线为x轴，所得方程为y2=2px-p2。

第三组：过定点F作垂直于l的直线交l于K，以FK的中点为原点，垂直于l的直线为x轴，所得方程为y2=2px。

教师：哪一组的结果正确？哪一组的结果最好？为什么？

学生：第三组的结果最好，它方程简单，结构很美。

教师：美在哪里？

学生：一是左边为二次项，右边为一次项；二是没有常数项。

教师：很好！下面我们一起来分析第三种方程的推导过程。

推出抛物线方程y2=2px后，得出抛物线的定义，点叫作抛物线的焦点，直线l：x=叫作抛物线的准线，正数p是抛物线的焦点到准线的距离，叫作焦准距。（板书）

用直接法求点的轨迹方程的过程：建系设点，列出等量关系，将点的坐标代入等量关系得方程，化简方程，证明（或说明）。

设计意图：通过分组讨论，一方面让学生巩固用直接法求轨迹方程的基本步骤，另一方面使学生感性认识抛物线的几何性质。

问题3：抛物线y2=2px(p＞0)有哪些特征？

（1）图像关于x轴对称；

（2）没有常数项；

（3）方程左边为二次项而右边为一次项；

（4）一次项的未知数是x（或y），图像就关于x轴（或y轴）对称。

设计意图：让学生体会抛物线方程的结构美和曲线的对称美，加深学生对抛物线标准方程及其性质的理解。

（三）概念深化

问题4：如果抛物线开口向左，那么它的标准方程又如何呢？它的焦点坐标和准线方程各是什么？抛物线开口向下或向上呢？

分组讨论，第一组讨论抛物线开口向左的情况，第二组讨论抛物线开口向上的情况，第三组讨论抛物线开口向下的情况，第四组自由讨论。

再由各组代表填写表1。

表1

续表

我们把上述四种位置的抛物线方程都称为抛物线的标准方程。

问题5：根据表1，四种不同形式的抛物线标准方程的相同点和不同点是什么？如何根据抛物线的标准方程判断焦点的位置？

焦点位置的判断方法：

在标准形式下，看一次项。若一次项的变量为x（或y），则焦点就在x（或y）轴上；若一次项的系数为正（或负），则焦点在正（或负）半轴。

四种不同形式的抛物线标准方程的共同特点：

（1）左边为二次项，且系数为1；

（2）右边为一次项；

（3）没有常数项；

（4）图像关于x轴或y轴对称；

（5）一次项的未知数是x或y，图像就关于x轴（或y轴）对称；

（6）焦点的非零坐标数是一次项系数的四分之一；

（7）准线方程中的非零常数项是焦点坐标中的非零坐标数的相反数。

设计意图：引导学生一起分析，推导出焦点在x轴正半轴的情况的标准方程，再类比得到其他三种情况。通过四种情况的观察、对比，引导学生发现抛物线的标准方程与图形之间的内在联系，从而得到一般性的规律，得出四种不同形式的抛物线标准方程的共同特点。

（四）应用探索

［例1］（1）已知抛物线的标准方程是y2=6x，求它的焦点坐标和准线方程；

（2）已知抛物线的焦点是F(0,-2)，求它的标准方程。

变式1：求下列抛物线的焦点坐标和准线方程。

（1）y2=20x（2）x2=y（3）x2=8y

设计意图：让学生体会由抛物线的标准方程求准线方程和焦点坐标，以及由抛物线的准线方程或焦点坐标求抛物线的标准方程的基本方法，加深对抛物线标准方程的结构的理解。

［例2］一种卫星接收天线如图2 所示，其曲面与轴截面的交线为抛物线。卫星波束呈近似平行状态射入形为抛物线的接收天线，经反射聚集到焦点处，已知接收天线的径口（直径）为4.8 m，深度为1 m。试建立适当的坐标系，求抛物线的标准方程和焦点坐标。

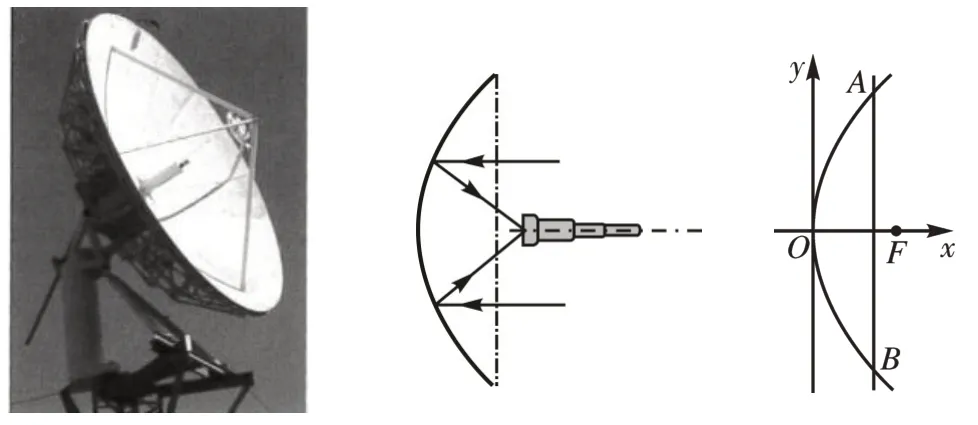
图2

设计意图：让学生体会用待定系数法求抛物线的标准方程的方法，初步了解抛物线知识在实际生活中的应用。

（五）小结

问题6：本节课你学到了哪些知识、技能和数学思想方法？

（1）抛物线的定义；

（2）抛物线的四种不同形式的标准方程、焦点坐标、准线方程；

（3）求抛物线标准方程的一般步骤；

（4）加深对类比法和待定系数法的理解。

设计意图：引导学生自我反馈、自我总结，并对所学知识进行提炼升华，让学生学会学习，掌握内化知识的方法和数学思想方法。

（六）布置作业

教材选修2-1第73页习题2.4A组第1、2、4题。

二、课例评析

“抛物线及标准方程”是继椭圆和双曲线后的一节新授课，教材通过几何画板演示，让学生对“平面内与一个定点F(c,0)的距离和一条定直线l（其中定点F不在直线l上）的距离相等的点的轨迹称为抛物线”有一个感性认识，然后类比椭圆和双曲线的学习方法推导出抛物线的标准方程，整个过程比较程序化，也比较枯燥。如何把问题讲活？如何让学生学会思考问题，让学生在活动中学习，同时又融入“立德树人”思想，体现教学的育人功能，达到学科育人的目的？笔者基于这样的思考设计了本节课的教学，教学设计能体现以下几个方面。

（一）能体现“立德树人”思想和史料育人功能

党的十八大报告明确指出：“把立德树人作为教育的根本任务，培养德智体美劳全面发展的社会主义建设者和接班人。”作为基础教育工作者，更应认真领会，坚定执行。课堂教学是培养学生道德认知、道德情感的主要途径。课堂上，教师不仅要传授给学生知识与技能，还要适时培养学生的道德认知和道德情感。

本节课通过展示赵州桥图片，让学生感受到中华文明的伟大；通过播放视频，让学生感受到体育健儿在努力为国争光。通过这样的教学设计，既能达到“立德树人”的目的，又能体现史料育人功能。

（二）能体现思维育人和活动育人功能

在教学中，让学生进行小组活动，类比椭圆和双曲线推导“平面内与一个定点F（c，0）的距离和一条定直线l（其中定点F不在定直线l上）的距离相等的点的轨迹方程”，通过小组活动探索“抛物线开口向左、向上、向下时的标准方程、焦点坐标、准线方程及其特点”以及“四种不同形式的抛物线标准方程的共同特点”，让学生在活动中学习，在活动中思考问题，在活动中解决问题，从而提高他们的认知能力和思维能力，培养他们的合作精神。这样的教学，既符合新课标的“将课堂还给学生”的要求，又符合“以学生为主体，以教师为主导”的教学理念，能充分体现思维育人和活动育人功能。

（三）能体现审美育人功能

党的教育方针是培养德智体美劳全面发展的社会主义建设者和接班人。“审美育人”既是教育方针要求，又是学科育人的基本要求。因此，教师要在教学中适时培养学生发现“美”的能力。本节课能体现“审美育人”的地方有：赵州桥设计之美，抛物线的图像对称之美，四种不同形式的抛物线标准方程、焦点坐标、准线方程的结构之美，等等。

数学学科的几个育人功能，即史料育人、思维育人、活动育人和审美育人，其实都是紧紧围绕着党的教育方针和党的十八大所提出的“把立德树人作为教育的根本任务，培养德智体美劳全面发展的社会主义建设者和接班人”。课堂教学是培养学生道德认知和道德情感的主要途径，也是学生获取知识、培养合作精神、发展思维的舞台。在课堂教学中，教师只要做个有心人，努力做到“随风潜入夜，润物细无声”，就一定能取得意想不到的效果。