“用数对确定位置”教学重点再理解

孙潇然

[摘 要]“用数对确定位置”一课的重难点在于将行列法改成数对法，使方位符号化，初步建立直角坐标系。为此，教学中，教师先以问题驱动，引导学生发现规则，创造数对;再绕开行列，引入数轴，接轨坐标;最后追本溯源，丰富结构，凸显符号思想。

[关键词]数对;确定位置;重点;解读;评析

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）05-0066-03

“用数对确定位置”是苏教版教材四年级下册的教学内容，此前学生已学过“第几排第几个”“第几行第几列”，其实这就是数对的知识，可教材为何还要编排“用数对确定位置”？有序数对“先列后行”的编排规定与日常生活中的“先行后列”的习惯相去甚远，教材为何非得使用数对表示位置？2011年版的课程标准中提到“让学生在具体情境中，能在方格纸上用点表示位置，能将数对与点位一一对应起来”，由此看来，用数学方法描述点的位置是教学总目标，因此“方法”“过程”“思想”缺一不可，应该整合起来。本课重难点是：将行列法改良成规范的数对法，扭转和纠正学生“行在前，列在后”的习惯;使方位符号化，初步建立直角坐标系。

一、问题驱动，发现规则，创造数对

【教师1】

（出示电影院座位表，学生尝试采用第几排第几个的方式来描述A观众的位置。）

师：如果请一位数学家来描述，他会用什么样的语言来描述呢？

师（板书：（4，2））：你们觉得这两个数字指的是什么？

生1：我认为指的是从上往下数第4排，然后从左往右数第2个座位。

生2：我认为是从下往上数第4排，然后从左往右数第2个座位。

生3：我觉得应该是从下往上数第2排的第4个座位;也有可能是从上往下数第2排……

师（圈出所有可能的点）：怎么会有这么多种可能？（暴露数对指向不明的问题）

师：老师再给出其他线索。A观众的好友也一起来看电影，他的座位用同样编排规则的数对（2，1）来表示。（教师在座位表上标出该友人的位置）

生4：这位友人的座位数对是（2，1），根据图示，正好是第2列、第1排。这样就清楚了，数对的前一个数表示列数，后一个数表示排数。A观众的座位位置数对是（4，2），说明他的座位在第4列、第2排，都是从左往右数列，从下往上数行。

【教师2】

（出示座位表，学生采用第几排第几个的方式描述A观众的座位在哪里。）

师：大家都能很好地描述座位了，那么接下来要学习什么呢？

生：我觉得应该有更简洁的表示方法。

师：那么到底可用什么方法来表示呢？现在就有请第四组的同学对“第3排第4个、第4排第3个”进行压缩改造，使其更简练。

（学生的探究结果如下：①4排3个;②4～3;③4·3;④竖4横3;⑤4↑3→;⑥4，3。）

师：每种方法似乎都很简练，到底哪一种才是正宗的数学方法呢？（生答略）

师：第⑥种方法才是正宗的数学方法：用行列来表示位置，并默認将列数写在前，行数写在后。

【解读与评析】虽然两位教师对于数对的引入方式不同，但都是在对行列表示法进行精简改良的基础上引入数对法。前者直接出示数学家的“数对”表示法，让学生根据一个已知数对和确切位置来推理两者的对应关系，而后者则是让学生自主构建编码规则，然后甄选出最优项。前者重在推导，后者重在探究。这样的教学设计已经很出色了，唯一值得商榷的是，这节课的学习目标是探寻“简洁方法”来确定座位，然后找到“有序数对”。然而“有序数对”就一定是最简洁的吗？日常用语中的“第几排第几个”“第几组第几个”已经通俗易懂、言简意赅了。如果硬要缩简，直接采用“几排几座”，比如“4排2座”，语意也很明确，而用（4，2），反而模糊了行列的界限。那么“有序数对”的价值在哪里？又用在哪里呢？其实课程标准已有明确的交代，即为了建立平面直角坐标系的雏形。数对其实就是坐标的前身，有了数对，点与点之间的距离计算、动点的轨迹描述就十分明了了。因此，在教学中应将座位图抽象成点阵图（如图1），并以点阵图为背景来探究数对表示法，促进学生建立动态位移的数对认知。比如，把点（1，5）每次右移1格，将会得到哪些点？（2，6）、（3，6）、（4，6）、（5，6）……（x，6），从这些点的坐标中可发现什么规律？如果把点（2，5）不断地上移或下移，得到的新坐标会有什么规律？把点（1，2）、（2，3）、（3，4）连成线，会有什么奇特的现象？以此类推，下一个点应该是什么？等等。由此使有序数对成为描述位置的新方法，让学生在新情境中感受数对表示法的优越性和准确性，并学会其规则。

数对的来源其实是为了解决平面坐标的确定问题，直线上的位置可以通过一个数来确定，而对于平面上的位置，由于存在横纵坐标，所以一个数字无法确定，投射到生活中就是对座位的确定和描述。一个平面内的座位，需要借助对行和列的限定才能最终确定，这个行和列其实就是平面坐标系里的横轴、纵轴，而行数和列数就是横纵坐标，只不过表述的顺序没有统一的标准，生活中习惯先说行后说列，而坐标系则是先横后纵，列数就是横坐标，行数就是纵坐标。再有，生活中的排列顺序很随意，行数的排列可以从左至右，也可以从右至左，列数的排列可以从上至下，也可以从下至上，而数学则是硬性规定的，横坐标从左至右，纵坐标从下往上。

二、绕开行列，引入数轴，接轨坐标

数对学习的经验基础是一年级的“方向”辨认，还有二年级的“找位置”的行列描述法，将两者结合起来就是数对表示法。经验是一把双刃剑，带来便利的同时也会形成负迁移，能否避开排与座、行与列这些惯用语呢？

【教师3】

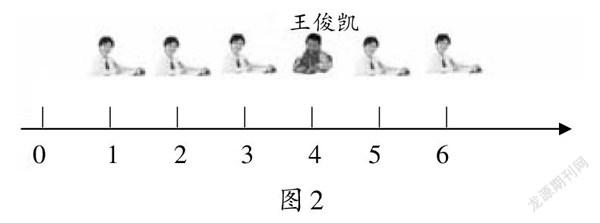
师（出示座位表，如图2）：谁能找出王俊凯的位置？

生1：从左往右数第4个。

师：图2有方向，也有数，像什么？

生2：数轴。

师：严格来说应该是横着的数轴，也叫作“横轴”，如果是竖着的数轴，则可称之为“竖轴”。

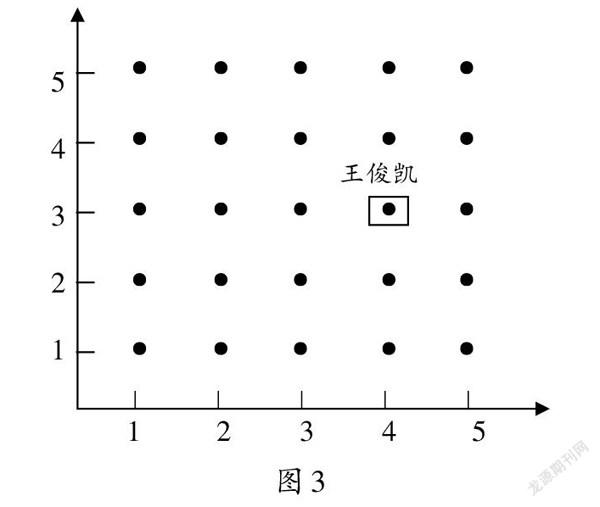
师：由生活中的位置可以联想到数学中的数轴。有了数轴，描述位置就变得简单易行了。（教师出示电影院的座位表，再抽象成点阵，如图3）

师：现在，如何表示王俊凯的位置？（学生探究后反馈交流）

生3：（4-3），（4·3），（4↑3→），（4，3）……

师：为了规范化，必须事先约定，先看所在列，再看所在行。列数一定，行数一定，位置也就唯一确定。为了以示区别，两数之间使用逗号间隔。这样的一对数称为数对，并用括号括起来表示，是一个整体。（板书：（4，3））

【解读与评析】怎样引出数对呢？利用已有经验，先从一维数轴切入，横着数就是从左至右，竖着数就是从下往上。因为是借助数轴，所以在数轴箭头的暗示下，数的方向非常明确。在二维坐标系中，学生先尝试描述位置，然后由教师介绍数对法——先从左到右横着数，再从下往上竖着数，简称“先横后竖”。这样教学直接抽象成数学点位，删减了实物对照，省去了优化过程，直接硬性规定先横看再竖看。想象力丰富的学生可能会在脑海中用符号“ ”过渡，而这先横后竖的形象，正好对应坐标系中的横纵坐标。用数轴教学，与生活化的“行列”描述法并不是格格不入的，如果是为了避开错误就弃用行列描述法，人为地将生活与数学割裂，也不利于学生从生活中抽象出坐标系的模型。而教完点阵图，再回归座位图，是一个不错的方法。

这种教法一开始就将数对的最本质特征暴露出来，先通过一排座位简单地引入，然后马上抽象出横向坐标轴，因为数轴自带方向性，不需要重新规定横轴的排列方向，接着自然提到将横轴竖起来就是纵轴，这样在类比之下，学生不需要花太多时间来认知纵轴。问题集中在先确定横坐标还是先确定纵坐标上，在象征性地让学生自由描述王俊凯的坐标位置后，教师直接提出硬性要求：必须统一标准，先看横坐标，再看纵坐标。这样规范的数对表示法就新鲜出炉了。最后回归平面直角坐标系，实际上就相当于回归到座位图，后期学生就会先入为主地尊奉这种坐标表示法，而行与列的说法则没有抬头的机会。

三、追本溯源，丰富结构，凸显符号思想

用数对确定位置不能粗暴地将“行、列、排、座”进行数学化处理，而是要有逻辑性地逐步推进。点的位置在线性、平面、立体空间中的参照维度不一样，有序数对是二维参照法。能不能根据空间延伸的层次性来展开教学呢？

【教师4】

师：今天老师请来了岳云鹏为大家说相声，只不过他藏身于幕后。（在黑板上画5个点）你们知道岳云鹏藏在哪里吗？

生1（疑惑）：每個点都有可能，信息量不够。

师（板书数字“2”）：现在呢？

生2：我觉得要么是顺数第二个点，要么是倒数第二个点，皆有可能。

师（标出方向“→”）：现在呢？

生3：从左至右第二个点。

师（画出5行5列共25个点）：岳云鹏此时又在何处？（板书（2，5），随后圈出所有可能的点）

师：还缺少什么信息？（画→，↑）这是什么含义？这样能帮你找到岳云鹏吗？

师：没错，就是从左至右第二列，从下往上第5行，可以用数对（2，5）表示。（2，5）在数学上叫数对，列在前，行在后，用括号括起来表示一个整体。你们会写了吗？

【解读与评析】以上教学中也用到了猜位置的游戏，略有不同的是，这是一个维度升级的发展变化过程：①在一维线段，确定点位只需要距离和方向，此时只需要一个数字和一个约定的方向。②在二维平面，学生发现一个数字和一个方向不够用了，需要两个数字和两个方向才能确定。教师“还缺少什么重要信息”的问题，既体现了对学生的尊重，又启示学生继续探索新的方法。像这样建立在维度升级上的引入，把一个几何概念的来龙去脉全部展示得清清楚楚。有的教师可能会质疑这种方法难度过大，其实适当加入数轴后，借助数轴，对应关系更加明显。毕竟，点与数对之间的一一对应关系是数形结合思想的生动体现。

很多教师都是将先学生置身于坐标图中，然后学生在错综复杂的方位中慢慢摸索，像走迷宫一样，教师再一步步引领学生找到合适的准确描述位置的方法，期间还要不断地强调和规定顺序，这很容易让学生迷失方向。而最后一种教法则可以完全避免上述麻烦。先让学生猜测位置，再让学生自己根据现实需要去创造规则和补充条件，由一个无序的坐标排列入手慢慢丰富各种线索。先完善横坐标的各项要素，然后扩充到平面二维坐标，让学生产生认知冲突，提出补充一个数字的需求，再根据数对（2，5）画出所有可能的位置，重复前面的操作，让学生自动迁移第一次的经验和做法，根据现实需要规定纵坐标的方向。整个过程逻辑严密，丝丝入扣，学生排除一切干扰，顺其自然地边操作边归纳出二维坐标的位置确定法。

综上，数学规则的形成既有人为规定的成分，又有科学发展的必然性，不同的解读方式产生不同的目标设定和教案。“教什么”与“怎么教”是一体两面，不可偏废。

（责编 罗 艳）