基于GeoGebra软件的可视化发展学生的直观想象素养

安振亚

摘  要：GeoGebra软件是一款集几何与代数于一体的可视化教学软件，能实现数学知识的多元表征，使静态的数学知识灵动起来. 在数学概念的生成、定理（或公理）的发现、模型的选择、例（习）题的解决及试题探究中，借助GeoGebra软件的可视化能有效发展学生的直观想象素养.

关键词：GeoGebra软件;可视化;直观想象;教学实践

一、问题提出

在我们生存的空间中，存在着各种各样的事物. 當我们把眼光聚焦在事物的空间形式和数量关系上的时候，这些事物就成为数学研究的对象. 由空间事物到数学问题一般需要经历观察、分析、比较、归纳和抽象概括等思维过程. 这有必要借助直观想象把空间事物图形化，依靠几何直观和空间想象发现问题、分析问题和解决问题. 在这个过程中，直观想象所引发的借形释数、化繁为简的思维习惯与思维方式，对学生自主学习数学甚至毕业后的工作与生活都很有价值. 既然直观想象如此重要，那么如何才能有效发展学生的直观想象素养呢？

数学可视化是将抽象的数学学习对象（概念原理、结构关系、思想方法等）用看得见的表征形式（图形、图象、动画等）清晰、直观地呈现出来，使人们对数学学习对象有一个形象、直观、整体的认识和理解. 在数学教学中，借助数学可视化软件使数学内隐部分外显化，是提升学生直观想象素养的有效途径.

GeoGebra软件是一款数学可视化教学软件，融合几何、代数两大学科，实现数学知识的多元表征，赋予静态的数学知识以灵动的动态演示与呈现，有效促进数学由科学形态向教育形态的转化. GeoGebra软件免费开源，操作简单，借助其可视化，能有效发展学生的直观想象素养.

二、发展学生直观想象素养的实践

在数学教学中，概念的生成、定理（或公理）的发现、模型的选择、例（习）题的解决及试题探究等都能成为培养学生直观想象素养的有效素材. 下面笔者谈谈在这些方面的一些教学实践.

1. 概念的生成

数学概念是对数学对象共性的概括，以一种思维形式存在，可以用来判定其他数学命题是否成立，也可以作为证明其他数学结论的基础. 要想让学生理解数学概念，就需要教师把概念中所隐含的数学思维打开，逐步呈现给学生，让学生在数学概念的生成过程中理解概念，把握数学概念的本质.

案例1：人教A版《普通高中教科书·数学》（以下统称“教材”）选择性必修第一册“抛物线概念的生成”的教学.

在“3.3 抛物线”一节课的引言中，教师通过类比椭圆、双曲线提出问题，并引导学生借助GeoGebra软件来解决这个问题.

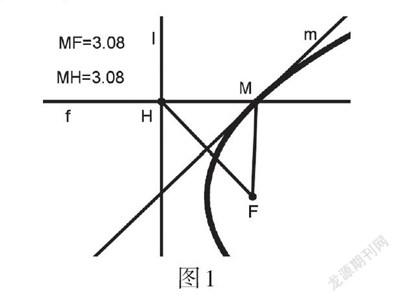
问题：动点[M]到定点[F]的距离与它到定直线[l]的距离相等时，动点[M]的轨迹是什么形状？

实验：如图1，在GeoGebra软件的绘图区创建定直线[l]和直线[l]外的定点[F];在直线[l]上创建点[H]和过点[H]且垂直于直线[l]的直线[f];创建线段[HF]和线段[HF]的垂直平分线[m];创建直线[f]与直线[m]的交点[M]与线段[MH，MF];右键开启追踪点[M]，拖动点[H]在直线[l]上运动，观察.

结论：动点[M]的轨迹是类似于二次函数图象的曲线，如图1所示.

然后，教师引导学生给抛物线下定义，并强调该定义的内涵.

感悟：GeoGebra软件虽然能凭借可视化的实验，生动展示抛物线的生成过程，为学生直观地理解抛物线的定义打下坚实的基础，但是有一点不能忽视，那就是引导学生自然想到动点[M]的构建过程.

2. 公理的发现

基本事实又叫公理，是由生活中的大量事实抽象出来的. 公理不需要证明而作为证明其他命题的依据. 公理的形成重在对事实的操作实验和归纳概括.

案例2：基本事实3（又称公理3）的操作实验.

关于公理3，教材必修第二册的第[126]页给出了思考：如图（图略），把三角尺的一个角立在课桌面上，三角尺所在平面与课桌面所在平面是否只相交于一点[B]？为什么？鉴于学生的空间想象力的局限性，在教学时，教师一般会利用教具做实验：让三角尺的一角立在桌面上，将一张纸沿着三角尺面滑向桌面，让学生观察纸的下边缘与桌面的接触情况. 进而得到结论：两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线. 该操作虽然直观地演示了一个平面“穿透”另一个平面的动态过程，但是由于客观因素的存在（如纸张的大小是有限的、纸张的下边缘是否能保持与桌面平行等），直观有余而效果达不到最优. 借助GeoGebra软件开展可视化实验，能给学生带来不一样的感受.

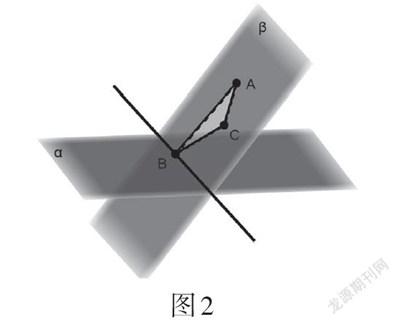
实验：如图2，在平面[α]内创建点[B]，在平面[α]外分别创建点[A，C];创建[△ABC];过点[A，B，C]创建平面[β];创建平面[α]与平面[β]的交线，该交线过点[B]. 拖动点[A，B，C]，改变三角形的形状，观察.

结论：平面[α]与平面[β]始终存在一条过点[B]的交线，如图2所示.

感悟：直线与平面是通过实际事物抽象出来的几何图形，其形状虽然可以用线段与平行四边形表示，但是它的完整形态主要还是借助空间想象来完成. 而GeoGebra软件凭借强大的[3D]功能，能够把三维空间的事物呈现出来，丰富学生的空间想象，进而有效理解问题.

3. 模型的选择

数学模型是从实际问题中抽象出来并用来解决实际问题的，体现了数学的工具性作用. 然而，数学模型的构建，牵涉的因素往往较多，仅仅靠纸笔运算来处理很难达到应用的教学效果.

案例3：某公司为了实现[1 000]万元利润的目标，准备制定一个激励销售人员的奖励方案：在销售利润达到[10]万元时，按销售利润进行奖励，且奖金[y]（单位：万元）随销售利润[x]（单位：万元）的增加而增加，但奖金总数不超过[5]万元，同时奖金不超过利润的25%. 现有三个奖励模型：[y=0.25x]，[y=log7x+1]，[y=1.002x]，其中哪个模型能符合公司的要求？

问题：选择奖励模型的依据是公司的要求，也就是激励销售人员的奖励方案. 可以用数学符号表示为[10≤x≤1 000，0≤y≤5，y≤0.25x.] 这三个函数哪一个符合上述约束条件呢？该问题涉及的函数较为复杂，数据处理较为烦琐，不借助信息技术很难达到应有的教学效果.

利用GeoGebra软件可以解决三个方面的问题.

（1）构造图象，直观判断哪一个函数模型符合公司的要求.

输入[y=0.25x]，[y=log7x+1]，[y=1.002x]，再輸入[x=][10]，[x=1 000]，[y=5]，把“[x]轴[∶][y]轴”设置为“[100][∶][1]”，如图[3]所示. 再把绘图区改为“标准视图”，如图[4]所示.

说明：通过该操作可以直观判断模型[y=0.25x]和模型[y=1.002x]不符合公司的要求，模型[y=log7x+1]符合公司的要求.

（2）构造交点，辅助代数运算.

用交点工具创建函数[y=1.002x]的图象与直线[y=5]的交点[A805.52，5]，函数[y=log7x+1]的图象与直线[x=1 000]的交点[B1 000，4.55]，如图5所示.

说明：通过该操作可以得到存在[x0∈805，806]，使得[1.002x0=5]. 当[x>x0]时，[y>5]. 排除函数[y=1.002x]. 由于函数[y=log7x+1]是增函数，且[log71 000+1≈4.55<5]，说明函数[y=log7x+1]满足条件[y≤5].

（3）构造图象，运用CAS运算，确定[y≤0.25x].

打开绘图区[2]，输入[gx=log7x+1-0.25x]，如图6所示.

说明：由图象，得函数[gx=log7x+1-0.25x]在区间[10，1 000]上单调递减，[gx≤g10]，只需判断[g10≤0].

打开CAS运算区，计算[g10=log710+1-0.25×][10≈-0.32<0].

说明：由[gx≤0]，得[log7x+1≤0.25x]，故当[x∈][10，1 000]时，[y≤0.25x]. 这说明按[y=log7x+1]奖励，奖金不会超过利润的25%.

感悟：数学教学应该注重信息技术与数学课程的深度整合，实现传统教学手段难以达到的效果. 就该案例而言，有两处是传统教学手段不易解决的问题：一处是画图不准确;另一处是求近似值有困难. 例如，计算[log1.0025]，[log71 000+1]，[g10]. 正是这个原因，造成了该案例成为实际教学中食之无味的“鸡肋”：要么不讲，安排学生自己阅读;要么给学生简单提示. 这样做就白白浪费了它在培养学生数学建模、直观想象等素养方面的育人价值. 而借助GeoGebra软件丰富的构图功能，能够为学生提供几何直观，进而做出合乎情理的判断. 当然，数学是“讲道理”的，利用GeoGebra软件得到的只是初步的判断，要想给出令人信服的结果，还需要严格的代数推理（运算）来论证. 而GeoGebra软件自身携带的运算区CAS能为代数运算提供强大的技术支持，让师生不再为计算而头痛.

4. 例题的解决

人教A版数学教材在部分章节中设置了数学在物理中的运用. 这些内容体现了数学是解决物理问题的工具，可以作为培养学生数学素养的材料.

案例4：教材必修第二册第[40]页的例[3].

在日常生活中，我们有这样的经验：两个人共提一个旅行包，两个拉力的夹角越大越费力;在单杠上做引体向上运动，两臂的夹角越小越省力. 你能从数学的角度解释这种现象吗？

思考1：以共提一个旅行包为例，要解决问题，我们需要弄清楚两个拉力的合力、旅行包所受的重力及两个拉力的夹角之间的关系. 设作用在旅行包上的两个拉力为[F1， F2]，夹角为[θ]，合力为[F]，所受的重力为[G]. 由力的平衡和向量的平行四边形法则，可以知道[F=G]，[F=F1]+[F2]. 其中[G]为定值. 我们借助GeoGebra软件来研究当夹角[θ]变化时[F1， F2]的大小变化情况.

实验1：如图7，当[F1=F2]时，在绘图区构建向量[AB=][G]，用旋转工具构建向量[AB]的相反向量[AB=F];创建滑动条[α]，范围为[0， π2]，增量为[0.002]. 用定值角度工具创建角[β=γ=α];以线段[AB]为对角线、以角[β，γ]的一边为方向作平行四边形[ACBD];创建向量[AC=F1]，[AD=F2];在绘图区[2]中输入[α，k]，其中[k=F1]，右键开启跟踪;拖动滑动条[α]，观察.

结论1：夹角[θ]越大，拉力越大;夹角[θ]越小，拉力越小;当[θ=0]时，拉力取最小值，如图7所示.

问题：若两个人的身高不同，手臂长也不同，则两个人的拉力如何？

思考2：由于两个人的身高与手臂长不同，因此两个拉力与合力[F]的夹角不同，那么问题就转化为：在合力一定的情况下，当夹角不同时，两个拉力的大小变化情况如何？

实验2：与实验[1]类似，滑动条[α]不变，拖动滑动条[β γ=β]，如图8所示;然后，滑动条[β]不变，拖动滑动条[α]，如图9所示.

结论2：当一个分力与合力的夹角不变时，另一个分力与合力的夹角越大，两个拉力也越大;夹角越小，两个拉力也越小.

感悟：利用GeoGebra软件开展可视化实验，可以为学生探寻到直观的结果，为进一步用代数方法验证结果指明了方向.

5. 试题探究

高考数学试题以数学知识为载体考查学生的数学知识、能力与素养，进而为高校选拔人才服务. 解高考试题可以巩固相关数学知识，查漏补缺，帮助学生形成较为完整的知识结构体系. 而探究高考试题则可以知晓试题的命制背景、考查目的，以及试题背后深层次的内容.

案例5：2020年高考数学全国Ⅰ卷理科第20题.

已知[A，B]分别为椭圆[E： x2a2+y2=1 a>1]的左、右顶点，[G]为[E]的上顶点，[AG · GB=8]，[P]为直线[x=6]上的动点，[PA]与[E]的另一交点为[C]，[PB]与[E]的另一交点为[D].

（1）求[E]的方程;

（2）证明：直线[CD]过定点.

解决该试题以后，我们会有一些疑问.

问题：如果椭圆[E： x2a2+y2b2=1 a>b>0]的左、右顶点分别为点[A，B]，点[P]为直线[l：x=h]上的动点，直线[PA]与[E]的另一个交点为[C]，直线[PB]与[E]的另一个交点为[D]，则直线[CD]是否也过定点？如果过定点，那么影响定点位置的因素有哪些呢？它与垂直于[x]轴的直线位置、椭圆的形状是否有关？或者说定点的横坐标与哪些参数有关？

针对这些问题，借助GeoGebra软件进行如下实验探究.

实验：如图10，在绘图区中，创建滑动条[a，b，h];輸入方程[x2a2+y2b2=1]，创建椭圆[E];输入方程[x=h]，创建直线[l];创建椭圆[E]与[x]轴的交点[A，B]，在直线[l]上创建一点[P];创建直线[PA，PB];创建直线[PA，PB]与椭圆[E]的交点[C，D];创建直线[CD];创建直线[CD]与[x]轴的交点[Q].

探究1：滑动条[a，b]不动，用鼠标拖动滑动条[h，]观察点[Q]的位置是否变化;然后滑动条[h]不动，用鼠标拖动点[P]在直线[l]上运动，观察点[Q]的位置是否变化，如图[10]所示.

结论1：定点的位置与垂直于[x]轴的直线位置有关，即点[Q]的横坐标与参数[h]有关.

探究2：滑动条[b，h]不动，用鼠标拖动参数[a]，观察点[Q]的位置是否变化;滑动条[a]不动，用鼠标拖动点[P]在直线[l]上运动，观察点[Q]的位置是否变化，如图[11]所示.

结论2：定点位置与椭圆的长轴有关，即点[Q]的横坐标与参数[a]有关.

探究3：滑动条[a，h]不动，用鼠标拖动参数[b]，观察点[Q]的位置是否变化;滑动条[b]不动，用鼠标拖动点[P]在直线[l]上运动，点[Q]的位置是否变化，如图[12]所示.

结论3：定点位置与椭圆的短轴无关，即点[Q]的横坐标与参数[b]无关.

然后，通过证明可以得到如下性质（该性质还可以推广到双曲线和圆）.

性质：若[A，B]分别为椭圆[E： x2a2+y2b2=1 a>b>0]的左、右顶点，[P]为直线[l：x=h h≠0]上的动点，[PA]与[E]的另一交点为[C]，[PB]与[E]的另一交点为[D]，则直线[CD]过定点[a2h，0].

感悟：这样一道看似平淡的高考试题，却有着丰厚的内蕴. 借助GeoGebra软件开展实验探究，不仅在于探究之后获得优美的结论，也在于探究过程中那独有的“风景”，以及沿途领略“风景”的心情. 对于学生而言，这正是打开一扇通往“探究之路”的大门，是培养学生问题意识、探究能力和创新思维的有效途径.

三、结束语

学生的直观想象素养是在数学概念的生成、定理（或公理）的发现、模型的选择、例（习）题的解决及试题的探究过程中潜移默化、润物无声地慢慢“生长”的，也是在直观、想象、再直观、再想象这样的循环往复中逐步发展的. 借助GeoGebra软件可以进行“形”与“数”的自由转换，建立可见形式与抽象形式的直接联系，满足学生发展直观想象素养的技术需求，帮助学生“窥视”数学的内部，推动学生的数学思维向更高层次发展，助力学生直观想象素养的有效提升.

参考文献：

[1]中华人民共和国教育部制定. 普通高中数学课程标准（2017年版2020年修订）[M]. 北京：人民教育出版社，2020.

[2]岳峻，杨忆婷. 数学可视化：提升直观想象素养的有效途径[J]. 中学数学教学参考（上旬），2021（8）：25-28.

[3]张志勇. 高中数学可视化情境的设计原则及实施路径[J]. 数学通报，2019，58（3）：15-19，24.

[4]岳峻. 指向数学学科核心素养的可视化教学：基于GeoGebra软件的数学可视化实验[J]. 中小学数字化教学，2021（8）：43-47.