高考全国卷与浙江卷中圆锥曲线客观题的对比研究
2022-04-18何波禄朱成万王红权
何波禄 朱成万 王红权



摘 要:从题量、分值、知识点等方面统计分析了2012—2021年高考数学全国卷与浙江卷在圆锥曲线客观题上的联系与区别,并提出几点教学思考.
关键词:数学高考;全国卷;浙江卷;圆锥曲线
自2004年以来,高考数学浙江卷均为自主命题,2004—2016年文、理分科,2017年新高考改革至今沿用文、理合卷模式,命题风格独树一帜. 2023年起,浙江省高考数学不再自主命题,将使用全国卷,而全国卷与浙江卷在命题风格、题型、考查知识点的侧重等多方面存在差异,这对浙江省的数学教学与复习备考带来了巨大的挑战. 为了迎接新高考、适应新高考,我们亟须研究高考全国卷的特点. 本文研究近十年(2012—2021年)高考中的圆锥曲线客观题(仅研究理科卷或文、理合卷,其中全国卷28份,浙江卷10份),分析它们的异同,以期对数学教学有所启发.
一、题量与分值对比分析
1. 题量、分值统计表
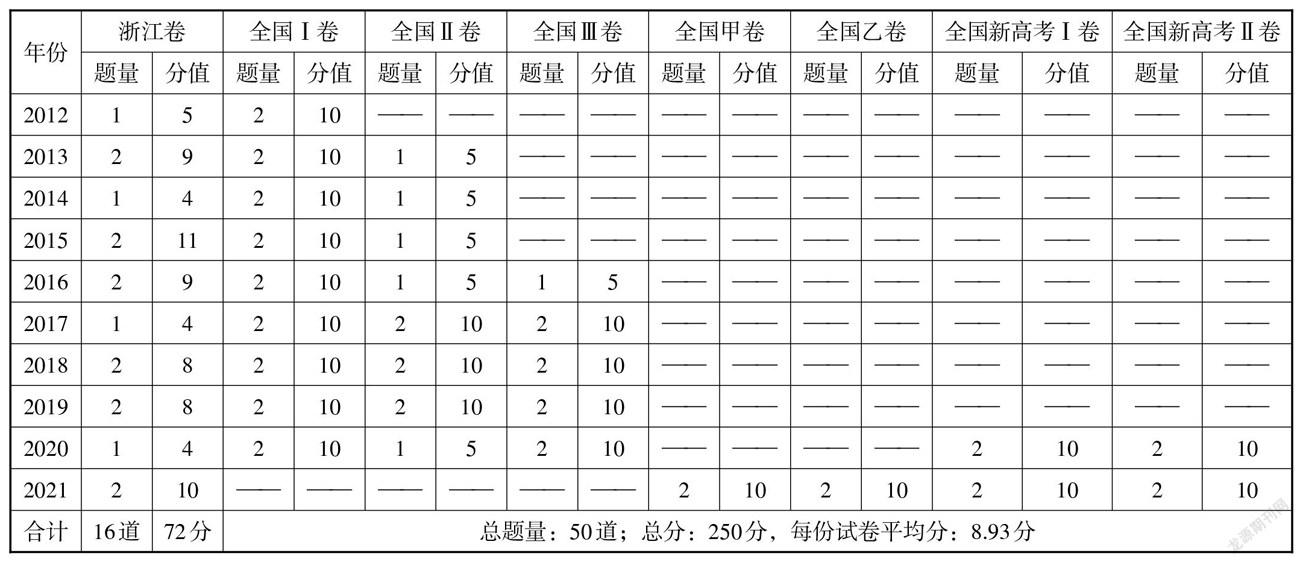
统计2012—2021年高考数学浙江卷与全国卷中圆锥曲线客观题的题量与分值,如下表所示. 其中,浙江卷2012—2016年为该年的理科试卷,2017—2021年为文、理合卷,共10份;全国卷2012—2019年均选择该年的理科试卷,2020—2021年为全国新高考试卷的文、理合卷,共28份.
2. 题量、分值分析
由上表可以看出,无论是全国卷还是浙江卷,圆锥曲线都是高考必考内容,也是重点考查内容之一,在试卷中的占比较大.
从题量来看,全国卷和浙江卷大多数有两道圆锥曲线客观题. 出现两道客观题的全国卷中约有一半试卷是一道选择题和一道填空题,另外一半是两道题均为选择题,而浙江卷中两道客观题均为一道选择题和一道填空题.
从分值来看,全国卷比较稳定,若题量为一道则分值为5分,若题量为两道则分值为10分,以10分为主,平均每份试卷中的圆锥曲线客观题分值为8.93分,约占总分(150分)的5.95%;浙江卷的分值从4分到11分不等,究其原因,主要是由于浙江卷中填空题分为单空题与双空题,平均每份试卷中圆锥曲线客观题所占分值为7.2分,约占总分(150分)的4.8%,低于全国卷.
二、知识点考查对比分析
1. 知识点考查统计图
2012—2021年高考数学浙江卷与全国卷中圆锥曲线客观题考查的知识点,主要包括椭圆、双曲线、抛物线的定义、标准方程与几何性质,直线与圆锥曲线的位置关系,圆锥曲线与圆、函数、平面向量、不等式等知识的综合与交会等,对每一类知识点分别计算出现的频率,得到下图.
2. 知识点考查分析
观察上图所示的知识点的频率分布图,不难发现全国卷与浙江卷在圆锥曲线客观题上的考查既有联系,又有区别.
全国卷与浙江卷考查范围广泛,几乎覆盖了圆锥曲线的各个方面,着力于考查圆锥曲线定义的应用,标准方程、几何性质等主干知识,突出学生对数形结合、函数与方程、转化与化归、分类与整合等数学思想、方法的理解与应用,重在培养学生的数学运算、直观想象、逻辑推理等数学学科核心素养. 两者在考查椭圆定义的应用、椭圆的标准方程与几何性质、双曲线定义的应用、双曲线的标准方程与几何性质上频率相当. 值得一提的是,全国卷与浙江卷在考查椭圆的标准方程与几何性质时出奇一致,往往需要求椭圆的离心率. 此外,两类试卷对双曲线的标准方程与几何性质内容上的考查最为频繁,其中双曲线的渐近线方程和离心率更是重中之重.
总体来说,全国卷与浙江卷的差异也很明显. 首先,全国卷中的试题均匀分布于易、中、难三个难度层次中,并未厚此薄彼;而浙江卷偏好于難题,对应试题处于选择题或填空题最后三道题的位置. 因此,圆锥曲线客观题是学生容易望而生畏的题型. 其次,全国卷中的试题更强调学生对基础知识的理解与掌握;而浙江卷综合性更强,需要运用多方面核心素养分析问题和解决问题. 因此,师生做题后的反馈是:浙江卷试题难,计算量大;全国卷相对容易,计算量小.
下面针对知识点,逐一进行分析与说明.
(1)椭圆、双曲线定义的应用. 全国卷和浙江卷在该内容上考查频率相当,基本上与其他知识(如平面几何、不等式、余弦定理或圆锥曲线的其他知识点)结合进行考查.
(2)椭圆的标准方程与几何性质. 全国卷与浙江卷在椭圆的标准方程与几何性质的考查上是同步的,频率一样且试题都是求椭圆的离心率,以难题的形式呈现.
(3)椭圆与直线的位置关系. 全国卷在近5年内未出现过椭圆与直线的位置关系的客观题,主要考查直线的斜率,均是中等难度的选择题;浙江卷分别在2018年、2019年和2021年考查直线与椭圆的位置关系,均是填空题中的难题,用于考查学生的综合能力,起到选拔优秀学生的作用.
(4)双曲线的标准方程与几何性质. 双曲线的标准方程与几何性质在所有知识点中占据了半壁江山,是高频考点. 试题涉及了双曲线的标准方程、实轴、虚轴、焦点、焦距、双曲线上点的取值范围、离心率、渐近线等众多知识点,常以基础题的形式呈现,偶尔会出现中等难度题. 在全国卷中出现频率较高的是利用渐近线求双曲线的离心率,利用离心率求渐近线方程,利用直线与渐近线关系的求解问题;浙江卷中则是利用直线与渐近线的关系求解离心率.
(5)双曲线与直线的位置关系. 双曲线与直线的位置关系的试题无论是全国卷还是浙江卷都是通过建立直线与双曲线的渐近线之间的关系来求解问题,我们将这类问题归纳于双曲线的标准方程与几何性质中.
(6)抛物线定义的应用. 此问题浙江卷近5年不曾设置,全国卷出现于2013年、2014年、2017年和2020年,浙江卷的频率略高于全国卷,同样以简单题的形式出现,是考查数形结合、函数与方程、转化与化归等数学思想的良好载体.
(7)抛物线的标准方程与几何性质. 全国卷在2021年全国新高考Ⅰ卷和全国新高考Ⅱ卷中分别考查了抛物线的标准方程与几何性质的内容,早些年也曾考查过,而浙江卷十年来从未有过其身影,全国卷与浙江卷对该部分内容的态度有着天壤之别.
(8)抛物线与直线的位置关系. 浙江卷早在2013年考查过一次抛物线中的弦中点问题,仅是昙花一现;与之相反,全国卷多次考查抛物线与直线的位置关系,尤其是在新高考试卷中,连续两年均有现身. 全国卷中该问题出现次数最多的为焦点弦的性质、焦点弦与不等式、三角形等的综合题.
(9)圆锥曲线与圆的关系. 全国卷分别考查过椭圆、双曲线、抛物线与圆的关系,求圆锥曲线的标准方程、几何性质,或求圆的标准方程. 浙江卷中从未出现过圆锥曲线与圆的关系的客观题.
(10)圆锥曲线综合问题. 圆锥曲线综合问题是指同时考查多个圆锥曲线相关知识点的试题,在全国卷和浙江卷中均有涉及. 全国卷对椭圆、双曲线和抛物线一视同仁,任意两者都有可能结合在一起考查,而浙江卷只对椭圆与双曲线的结合情有独钟. 此外,2020年全国新高考Ⅰ卷还以多选题的方式对该知识点进行考查,难度更上一个档次.
3. 考查内容的理解
全国卷本着“一核”“四层”“四翼”的评价理念,注重学科特点,从学科思维价值和整体高度的角度出发,突出了数学知识的基础性与综合性,以圆锥曲线的重点知识和主干知识为主体,着意将数学知识运用的灵活性与创新性,数学能力与数学素质融为一体,全面检测了学生的数学学科核心素养.
(1)强调基础.
著名数学家苏步青曾说,扎扎实实地打好基础,练好基本功,是学好数学的秘密. 高中阶段圆锥曲线这一内容,秉承了注重概念,基础常规,讲究通性、通法的理念.
例1 (2021年全国新高考Ⅱ卷·13)已知双曲线[x2a2-y2b2=1 a>0,b>0]的离心率[e=2],则该双曲线的渐近线方程为 .
【评析】该题主要考查双曲线离心率的应用及渐近线方程的求解,考查了双曲线基础知识的应用. 试题比较简单,以学生喜闻乐见的方式呈现,体现基础性.
(2)重视数形结合.
圆锥曲线是平面解析几何中的重要内容,而解析几何是沟通代数与几何的桥梁,因此数形结合思想在圆锥曲线中有着广泛的应用.
例2 (2021年全国甲卷·理15)已知[F1,F2]为椭圆[C: x216+y24=1]的两个焦点,[P,Q]为[C]上关于坐标原点对称的两点,且[PQ=F1F2],则四边形[PF1QF2]的面积为 .
【评析】该题有部分学生会利用解析法设点[P]的坐标,根据两点间的距离公式与椭圆方程联立进行运算求解,虽然求解难度不大,但需要花费一定的时间且容易算错. 事实上,我们可以根据椭圆的对称性及已知条件得到四边形[PF1QF2]是矩形,再结合椭圆定义的应用与勾股定理求解四边形面积,此方法充分体现了数形结合思想在圆锥曲线中的妙用.
(3)注重数学运算素养.
《普通高中数学课程标准(2017年版)》中指出,数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养,主要包括理解运算对象、掌握运算法则、探究运算思路、选择运算方法、设计运算程序、求得运算结果等. 数学运算是解决数学问题的基本手段,尤其是在圆锥曲线中,我们要通过数学运算促进学生的数学思维发展.
例3 (2021年全国乙卷·理11)设点[B]是椭圆[C: x2a2+][y2b2=1 a>0,b>0]的上顶点,若[C]上的任意一点[P]都满足[PB≤2b],则[C]的离心率的取值范围是( ).
(A)[22,1] (B)[12,1]
(C)[0, 22] (D)[0, 12]
【评析】该题通过两点间的距离公式表示出[PB],得到[PB2]是关于点[P]纵坐标的一个二次函数,根据椭圆上的点的纵坐标的取值范围,分类讨论求最大值,最后构建不等式求解离心率的取值范围. 该题属于圆锥曲线中的难题,对二次函数在给定区间内求最值是学生容易出错之处. 重点考查分类讨论、转化与化归等数学思想,对学生的数学运算素养有较高要求,要求“算理”与“算力”并重.
三、教学建议
1. 改变是必经之路
综合以上分析,全国卷与浙江卷在圆锥曲线客观题的考查上既有联系又有区别,且区别更大. 例如,浙江卷命题偏向于难题,而全国卷起点低、坡度缓,兼顾易、中、难三个难度层次;浙江卷综合性更强,常与直线、圆、三角形、函数、平面向量、不等式等多个知识交会考查,而全国卷更注重考查定义、方程、性质等;浙江卷解题灵活多变且运算量大,全国卷更具有规律性,思路简单,计算量小. 从具体知识点角度来讲,全国卷与浙江卷在椭圆与直线的位置关系、双曲线的标准方程与几何性质、抛物线定义的应用、抛物线的标准方程与几何性质、抛物线与直线的位置关系、圆锥曲线与圆的关系和圆锥曲线综合问题等方面均有所差异. 若仍以浙江卷的命题风格组织教学,必将四处碰壁. 因此,浙江省的教师要聚焦全国卷的特征,以全国卷为向导,改变对浙江卷的思维定式.
2. 落实数学思想方法是紧要任务
圆锥曲线的试题中蕴含许多数学思想. 例如,数形结合思想,利用图形性质来研究数量关系是解析几何的常用方法;函数与方程思想,试题中若有元素處于运动变化中,则可以构建函数解决;分类讨论思想,分类讨论使解题过程更加缜密、严谨,分类讨论时要注意做到有根有据,不重不漏;转化与化归思想,圆锥曲线试题中往往会通过定义将复杂问题转化为简单问题;等等. 这些思想与方法并不是彼此孤立的,往往需要结合起来,多管齐下. 教师在日常教学中应帮助学生对圆锥曲线中的不同题型、不同解题思路进行反思和总结,体会并熟练应用数学思想与方法.
3. 提升核心素养是关键
圆锥曲线是平面解析几何的核心内容,是高考重点考查的内容之一,考查学生的逻辑思维能力、运算能力、空间想象能力、分析和解决问题的能力等. 对学生的数学运算、直观想象、逻辑推理等数学学科核心素养有较高要求,特别是数学运算与直观想象素养,而逻辑推理则是利用“形”的特征,结合圆锥曲线的定义与平面几何的有关性质将其转化为代数运算,也即逻辑推理素养需要借助数学运算与直观想象来实现. 在平时的教学中,教师应注重数形结合,巧选运算方法,优化运算过程,形成必要的思维模式,从而提升学生的数学学科核心素养.
参考文献:
[1]朱成万,王红权. 至精至简的数学思想与方法(第四版)[M]. 杭州:浙江大学出版社,2020.
[2]教育部考试中心制定. 中国高考评价体系[M]. 北京:人民教育出版社,2019.
